Appel W. Mathematics for Physics and Physicists

Подождите немного. Документ загружается.

Singularities at inﬁnity 147

′

Fig. 5.4 — The Riemann sphere, obtained by stereographic projection. I f z is a point in

the complex plane C, the line (N z) meets the sphere centered at 0 with radius 1

in a singl e point z

′

, the image of z on the Riemann sphere. The equator of

the sphere is the image of the circle ce ntered at the origin with radius 1. The

point N corresponds to the point at inﬁnity (and to “going to inﬁnity” in all

directions).

The entire functions which have a pole at inﬁnity are (only) the polyno-

mials.

Remark 5.23 The deﬁnition of the residue at inﬁnity is justiﬁed by t h e fact that it is not really

the function f w h ich matters for the residue but rather the differential form f (z) d z (which

is th e natural object occuring in the theory of p ath integration; see Chapter 17). By putting

w = 1/z, it follows that

f (z) dz = −





dw = −

F (w) dw.

The residue theorem can then be extended to the Riemann sphere:

THEOREM 5.24 (Generaliz ed residue theorem) Let Ω be an open subset of C

(the topology of which is that of a sphere in space by stereographic projection) and

K a closed subset with oriented boundary γ = ∂Ω which is made of one or more

closed paths in C (hence not passing through the point at inﬁnity). Let f be a

function holomorphic on Ω, except possibly at ﬁnitely many p oints. Denote by z

the

singularities of f inside K; then

f (z) dz = 2πi

Res ( f ; z

where the sum ranges over the singularities, including possibly the point at inﬁnity.

Proof. It suf ﬁc es to treat the case whe re the point at inﬁnity is in the interior of K .

Assume that all the ﬁnite singularit ies (in C) are contained in the ball B(0 ; R). The

set {|z| > R} is then a neighborhood of ∞, which we may assume is contained in K

(increasing R if need be). We then deﬁne K

′

= K \



z ∈ C ; |z| > R



, which has a

boundary given by

∂ K

′

= γ ∪C (0 ; R)

(with positive orientation). Applying the residue theorem to K

′

, we ﬁnd

f (z) dz +

|z|=R

f (z) dz = 2πi

ﬁnite

singularities

Res ( f ; z

148 Complex Analysis II

Thus we obtain

|z|=R

f (z) dz =

|w|=1/R





dw = −2πi Res ( f ; ∞).

(Note that the change of variable w = 1/z transforms a positively oriented contour to

a negatively oriented one.)

The stated formula follows.

Example 5.25 The function f : z 7−→1/z has a pole at inﬁnity, with residue equal to −1.

If we let γ = C (5 ;1), a contour which does not contain any singularity in C, we have

f (z) dz = 0.

Using the generalized residue theorem

, we get

f (z) dz = 2iπ

Res ( f ; 0) + Res ( f ; ∞)

= 2iπ(1 −1) = 0.

∞

5.5

The saddle point method

The saddle point meth od is a computational “recipe” developed by Debye

to compute integrals of the type

I(α)

def

−α f (z)

dz.

Here, z is a real or complex variable.

The goal is to ﬁnd an approximation

of I(α) in the limit when α goes to +∞, assuming that the function f admits

a local minimum.

With respect to the closed set K which is the “outside” of γ on the picture. In fact, the

notions of the parts “inside” and “outside” a curve do not make sense on the Rie mann sphere.

Which side is the “outside” of the equator on Earth? The northern hemisphere or th e southern

hemisphere?

Pe trus Joseph u s Wilhelmus Debye (1884—1966), a Dutch physicist, born in Maastricht, stud-

ied the spec iﬁc heat of solids (Debye model), ionic solutions (De bye potential, see problem 5

p. 325, Debye-Hückel metho d), among other things. He received the Nobel prize in chemistry

in 1936.

There exist generalizations of this method for functions of vector variables, even for ﬁelds,

which are used in quantum ﬁeld theory.

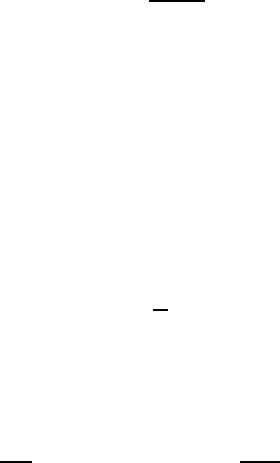
The saddle point method 149

5.5.a The gene r al saddle point method

Consider, more generally, an integral of the type

def

−f

(z)

dz, (5.6)

where α is a complex parameter and γ is a path in C. We assume that f

a function analytic on an open subs et containing γ, and we want to evaluate

this integral in the limit where |α| → ∞.

The ﬁ rst idea is to evaluate the integral in the parts of the domain of

integration where the real part of f

is minimal, since it is in those regions

that the modulus of exp

−f

is largest and so they should bring the main

contribution to the integral. Unfortunately, in those regions, the imaginary

part of f may very well vary and, therefore, e

−f

will oscillate, possibly very

rapidly. These oscillations may well destroy a large part of the integral by

compensations, and the suggested method will not be justiﬁed.

The idea of Debye is then to deform the contour γ into an invented path γ

satisfying the following properties:

i) along γ

, Im



(z)



is constant;

ii) there exists a point z

on γ

such that

d f

(z)



= 0;

iii) the real part of f

has a local minimum at z = z

;

iv) moreover, this minimum becomes “steeper and steeper”;

v) ﬁnally, the initial path γ can be deformed continuously into γ

(i.e.,

during the deformation, it must not pass through any of the singulari-

ties of f

DEFINITION 5.26 A point of C s atisfying Conditions ii) and iii) above is

called a saddle point for f

The condition Im



(z)



= C

gives, in general, the equation for the

curve γ

. Under this condition, the phase of the ex ponential is constant, and

the computation reduces to a real integral.

Consider now the behavior of the function f

around the sa ddle point, if

it exists. Suppose therefore that

d f



z=z

= 0 and



z=z

6= 0.

150 Complex Analysis II

Then we can write

(z) = f

) +

(z − z

)



z=z

+ o(z − z

)

. (5.7)

Denoting



z=z

= ρ e

iθ

and z − z

= r e

iϕ

we have, as a ﬁrst approximation,



(z) − f

)



ρ cos(2ϕ + θ) + o(r



(z) − f

)



ρ sin(2ϕ + θ) + o(r

Hence we see that, at the saddle point z

, the angle ϕ between the path γ

and the real axis should be such that sin(2ϕ + θ) = 0, which leaves two

possible directions, orthogonal to each other (solid lines in Figure 5.5). The

two directions characterized by cos(2ϕ + θ) = 0 are those where the real part



(z) − f

)



is constant. Between those lines, the real part is either

positive or negative, depending on the sign of cos (2ϕ + θ), which shows that

we are indeed dealing with a saddle point, or a “mountain pass” (see Figure 5.5).

The two orthogonal directions where th e imaginary par t of f

(z) − f

)

vanishes (to second order) are precisely the directions where the real part of

(z) − f

) varies most quickly, either increasing or d ecreasing.

Consequently, we must choose, at the saddle point, the direction charac-

terized by sin(2ϕ + θ) = 0 and such that, along this direction, Re( f

) has a

local minimum at z

, and not a local maximum.

We have seen that, because of the properties of holomor phic functions, it

is usually possible to ﬁnd a path along w hich the oscillations of e

−f

have dis-

appeared a nd where, moreover, f

will have a local minimum as pronounced

as possible. This justiﬁes the other common name of the method: the method

of steepest descent.

There only remains to evaluate the integral along the path γ

. We intro-

duce a new variable t parameterizing the tangent line to γ

at z

, so that we

can write

(z) = f

) +

+ o(z − z

)

and, f rom (5.7), we have

t = (z − z

)

(the sign of the square root being chosen in such a way that its real part is

positive). We now rew rite formula (5.6) in terms of this parameter t, which

gives, noticing that dz =



dz(t)/dt



dt,

≈ e

−f

)

+∞

−∞

−t

dz(t)

dt.

The saddle point method 151

Re( f )

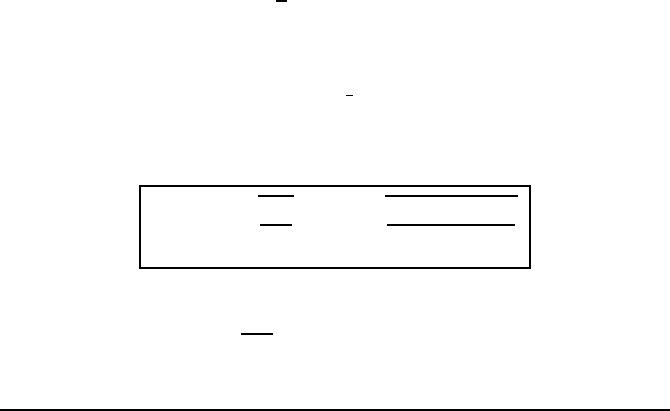
Fig. 5.5 — The two solid curves are perpendicular and locally determined by the condition

sin(2ϕ + θ) = 0. These are not only the curves such that Im( f

) is constant,

but also those where Re( f

) varies most rapidly. The two dotted lines separate

the regions a, b, c and d. In regions a and c, Re f

(z) > Re f

), whereas in

regions b and d, Re f

(z) < Re f

). The chosen path therefore goes through

regions a and c.

Since the function d f

/dz varies slowly in general, compared to the ga us sian

term, we can consider that dz/dt = (d

/dz

)

−1/2

is constant, and evaluate

the remaining gauss ian integral, which gives

≈ e

−f

)

(

2π

/dz



z=z

)

1/2

. (5.8)

This formula can be rigorously justiﬁed, case by case, by computing the non-

gaussian contributions to the integral and comparing them w ith the main

term we just computed. The computation must be done by expanding f

higher order. One is then led to compute gaussian moments (which is easy) to

derive an asymptotic expansion of I

to higher order. A condition to ensure

that the h igher orders do not interfere is that the ratio between



x=x

1/p

and



x=x

1/2

tends to 0 when α tends to inﬁnity. This condition is necessary, but not

sufﬁcient.

152 Complex Analysis II

5.5.b The real saddle point method

There exists a particularly simple case of the problem when f is a real-valued

function. Then it is not possible to work in the complex plane, but a gaussian

integral computation leads to a similar result.

Consider an integral of the shape

−f

(x)

dx,

where f

is a f unction at least twice continuously differentiable, depending on

a parameter α, and with the following property:











for every α, f

has a unique minimum

at a point x

, de-

noted m

= f

); moreover, this minimum is more and

more “narrow”; i.e., if we d enote M

def

= d

/dx



x=x

, we

have M

> 0 and M

−→ +∞ as α → ∞.

(5.9)

The dominating contribution to the integral is evidently given by the

region of x close to the local minimum. So the idea is to expand the function

around this minimum. If it sufﬁces to expand to order 2 (the ﬁrst derivative

is zero because the point is a local minimum), then the computation reduces

to a gauss ian integral. This approximation should b e all the more justiﬁed as

we ta ke the limit [α → ∞].

We thus w rite

(x) = m

(x − x

)

+ o(x − x

)

and as a ﬁrst approximation estimate the integral by

≈ e

−m

−

(x−x

)

dx.

We recognize here a gaussian integral, so the result is

≈ e

−m

2π

= e

−m

2π

/dx



x=x

The ﬁrst factor is simply the value of the exponential function at its maxi-

mum, and the second factor expresses the “characteristic width” of t his maxi-

mum, proportional to 1/

. Th is result should be compared to the result

of (5.8).

If f

has several local minima, each one contributes to the integral.

Exercises 153

Remark 5.27 Sometimes, an integral of the same type as before arises, but with an imaginary

exponential, that is, of the t ype

i f

(x)

dx,

where f

is a real-valued function.

In th is case, if f

) varies fast enough as α tends to inﬁnity for a gi ven x

, we expe ct that

the neigh borhood of this point will only have a small contribution to the integral, becau se

of destructive interferences. This phenomenon can be understood “by hand” by the following

rough reasoning: if we expand around x

(x) = f

) + (x − x

)

d f



x=x

+ o(x − x

and i f d f

/dx 6= 0, we have, as a ﬁrst approximation, an integral of th e type

ik(x−x

)

dx, with k

def

d f



x=x

which is zero if k 6= 0.

We must therefore look for extremums of f

to ﬁnd important contributions, which are

called for obvious reasons stationary phase points; assuming there is a unique such point x

, a

computation very similar to the previous one for the real saddle point method gives the result

≈ e

i f

)



2πi

/dx

x=x



1/2

This case is also called the stationary phase method.

Remark 5.28 The saddle point method is not just a t rick for physic ists. It is very often used

in pure mathematics, analytic number theory in particular; for instance, it occurs in the proof

of the irrationality of one of the numbers ζ (5), ζ(7), . . . ,ζ (21) by Tanguy Rivoal [73 ]! (Recall

that

ζ (s) =

n¾1

for Re(s) > 1).

EXERCISES

 Exercise 5.1 Deﬁne

u(x, y) = e

(x c o s y + µ y sin y).

Find µ so that u is the real part of a holomorphic function f (identifying the plane R

and

the complex plane). What is the function f ?

 Exercise 5.2 Similarly, ﬁnd all the holomorphic functions w ith real par t equal to

P (x, y) =

x(1 + x) + y

(1 + x)

+ y

 Exercise 5.3 Show that, in two dimensions, a cavity in a conductor, devoid of charge, has

potential identically zero.

154 Complex Analysis II

 Exercise 5.4 (Stirling formula) Using the Euler Γ function deﬁned on t he complex half-

plane Re(z) > 0 by the integral representation

Γ(z)

def

+∞

−x

z−1

dx,

and using th e fact that Γ(n +1) = n! for all n ∈ N, show, by the complex saddle point method,

that

Γ(n + 1) = n! ∼ n

−n

2πn.

This formula, established by Abraham de Moivre, is called the Stirling formula.

SOLUTIONS

 Solution of exercise 5 .3. Denote by Ω the domain deﬁned by the cavity; Ω is simply con-

nected. The electrosatic potential satisﬁes ϕ(z) = 0 at any point z ∈ ∂Ω. This potential i s also

a harmonic function, hence achieves its minimum and its maximum on the boundary ∂Ω.

Consequently, we have ϕ(z) = 0 for any z ∈ Ω.

 Solution of exercise 5 .4. The ﬁrst thing to do is to ﬁnd a suitable contour. To start with,

write

Γ(α + 1) =

+∞

−x−α log x

dx,

then look for th e points where d f

/dz = 0, w ith f

(z) = z − α log z. We ﬁnd z

= α, and

/dz

= 1/α, which i s a positive real number. The two lines for which, locally, the

imaginar y part of f

is constant are the real axis and the line with equation z = α + i y. It is

the ﬁrst which corresponds to a local minimum of f at z

= α; therefore the real axis is the

most suitable contour.

Hence we evaluate the integral according to the formula (5.8), which gives

Γ(α + 1) ≈ e

−α−α logα

2πα [α → ∞].

One can check explicitly that th e non-gaussian contributions (those given by the terms of order

larger than 2 in the expansion of f

) are inverse powers of α. Hence

Γ(α + 1) = α

−α

2πα



1 + O (1/α)



and i n particular, for integral values of α,

Γ(n + 1) = n! ∼ n

−n

2πn.

Notice that this approximation is very quickly quite precise; for n = 5, the exact value is

5! = 120 and the Stirling formula gives approximately 118, which is an error of about 2%.

Even more impressive, the relative error from applying the Stirling formula for n = 100 is

about 0, 08%. . . (note that this error is neverth eless very large in absolute value: it is roughly of

size 10

155

, whereas 100! is about 10

158

Remark 5.29 If one seeks the asymptotic behavior of Γ(z) for large z not necessarily real, the

computation is more or less the same, except that the path γ is not the real axis any more.

However, th e result of the computation is identical (the result is valid uniformly in any region

where the argument θ ∈ ]−π, π] of z satisﬁes −π + ǫ < θ < π −ǫ for some ǫ > 0).

Chapter

Conformal maps

6.1

Conformal maps

6.1.a P reliminaries

Consider a change of variable f : (x, y) 7→ (u, v) =



u(x, y), v(x, y)



in the

plane R

, identiﬁed with C. This change of variable really only deserves the

name if f is locally bijective (i.e., one-to-one); this is the case if the jacobian

of the map is nonzero (then so is the jacobian of the inverse map):



D(u, v)

D(x, y)



∂ u

∂ x

∂ u

∂ y

∂ v

∂ x

∂ v

∂ y



6= 0 and



D(x, y)

D(u, v)



∂ x

∂ u

∂ x

∂ v

∂ y

∂ u

∂ y

∂ v



6= 0.

THEOREM 6.1 In a c omplex change of variable

z = x + i y 7−→ w = f (z) = u + iv,

and if f is holomorphic, then the jacobian of the map is equal to

(z) =



D(u, v)

D(x, y)



′

(z)



156 Conformal maps

Proof. Indeed, we have f

′

(z) =

∂ u

∂ x

+ i

∂ v

∂ x

and hence, by the Cauchy-Riemann

relations,



′

(z)





∂ u

∂ x





∂ v

∂ x



∂ u

∂ x

∂ v

∂ y

−

∂ v

∂ x

∂ u

∂ y

= J

(z).

DEFINITION 6.2 A conformal map or conformal transformation of an

open subset Ω ⊂ R

into another open subset Ω

′

⊂ R

is any map f :

Ω → Ω

′

, locally bijective, that preserves a ngles and orientation.

THEOREM 6.3 Any conformal map is given by a holomorphic function f such that

the derivative of f does not vanish.

This justiﬁes the next deﬁnition:

DEFINITION 6.4 A conformal transformation or conformal map of an

open subset Ω ⊂ C into another open subset Ω

′

⊂ C is any holomorphic

function f : Ω → Ω

′

such that f

′

(z) 6= 0 for a ll z ∈ Ω.

Proof that the deﬁnitions are equivalent. We will denote in general w = f (z).

Consider, in the complex plane, two line segments γ

and γ

contained inside the set

Ω where f is deﬁned, and intersecti ng at a point z

in Ω. Denote by γ

′

and γ

′

their

images by f .

We want to show that if the angle between γ

and γ

is equal to θ, then the same

holds for their images, which means that the angle between the tangent lines to γ

′

and

′

at w

= f (z

) is also equal to θ.

Consider a point z ∈ γ

close to z

. Its image w = f (z) satisﬁes

lim

z→z

w − w

z − z

= f

′

and hence lim

z→z

Arg(w − w

) −Arg(z − z

) = Arg f

′

which shows that the angle between the curve γ

′

and the real axis is equal to the angle

between the original se gment γ

and the real axis, plus the angle α = Arg f

′

) (which

is well deﬁned because f

′

(z) 6= 0).

Similarly, the angl e between the i mage curve γ

′

and the real axis i s equal to that

between the segment γ

and the real axis, plus the same α.

Therefore, the angle between the two image curves is the same as that between the

two line segments, namely, θ.

Another way to see this is as follows: the tangent vectors of th e curves are trans-

formed according to the rule v

′

= d f

v. But the differential of f (when f is seen as

a map from R

to R

) is of the form

d f







∂ P

∂ x

∂ P

∂ y

∂ Q

∂ x

∂ Q

∂ y









′

)





cos α −sin α

sin α cos α



, (6.1)

where α is the argument of f

′

). This is the matrix of a rotation composed with a

homothety, that is, a similitude.