Appel W. Mathematics for Physics and Physicists

Подождите немного. Документ загружается.

Applications to potential theory 167

6.2.b Application to hydrodynamics

Consider the bidimensional ﬂow of a perfect ﬂuid (i.e., an incompressible, non-

viscous, and irrotational ﬂuid). Then (see, for instance, the excellent book by

Guyon et al. [44]) the ﬂ uid velocity is obtained locally, at any point, from a

potential ϕ, in the sense th at the x and y coordinates of the velocity are given

∂ϕ

∂ x

and v

∂ϕ

∂ y

This potential is harmonic since div v = 0 is equivalent to △ϕ = 0. Solving

the ﬂow problem amounts to ﬁnding ϕ with the right boundary conditions

(normal velocity equal to zero on all impenetrable surfaces). This is called the

Neumann problem.

Remark 6.18 The velocity is obtained from a global potential if the domain under

consideration Ω ⊂ C is simply connected. Otherwise, it may not be possible to ﬁnd a

global potential; it is then necessary to “cut” Ω into simply connected pieces, and try,

after solving the problem on each component, to glue the solutions back toget her. In

what follows, we assume that Ω is indeed simply connected.

DEFINITION 6.19 The complex velocity of the ﬂuid is the complex quantity

given by

def

= v

+ iv

Since ϕ is harmonic, we know (Theorem 5.13) that there exists a harmonic

function ψ : Ω → R which is conjugate to ϕ, that is, such that Φ

def

= ϕ + iψ is

holomorphic on Ω. T hen the complex derivative of Φ is the conjugate of the

complex velocity:

′

(z) =

∂Φ

∂ z

∂Φ

∂ x

∂ϕ

∂ x

+ i

∂ψ

∂ x

Cauchy-Riemann

∂ϕ

∂ x

−i

∂ϕ

∂ y

= v

−iv

= V (z).

The complex velocity is therefore an antiholomorp hic function.

DEFINITION 6.20 The holomorphic f unction Φ is called the complex poten-

tial. A stagnation point for the ﬂow Φ is any point z

∈ Ω wh ere the complex

velocity vanishes: Φ

′

) = 0.

Consider, for instance, the ﬂow of a perfect ﬂuid in a domain D in R

(identiﬁed with the complex plane C), delimited by the ground and by a wall

Carl Gottfried Neumann (1832—1925), Ge rman mathematici an and physicist, was the son

of the physicist Franz Ernst Neumann, who introduced the notion of potential in electromag-

netism.

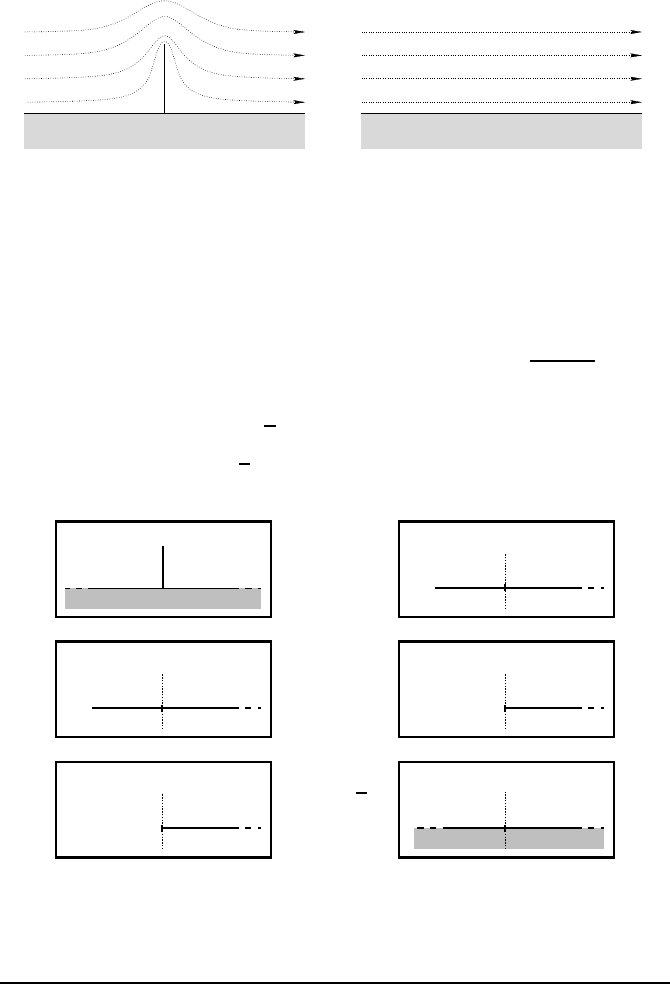
168 Conformal maps

z w = f (z)

Fig. 6.4 — On the left: the wind over a wall. The white region is D. O n the right: the

wind over the ground, without a wall. The white region is D

′

of height a (see Figure 6.4, left). We w ill, by a conformal transformation,

map D into the upper half-plane

′

def



z ∈ C ; Imz > 0



(see Figure 6.4, right). For t his, it is enough to put f (z) =

+ a

= w.

Indeed, if we decompose t he transformation f in t hree steps

f = (z 7→

z) ◦(z 7→ z + a

) ◦(z 7→ z

where the function z 7→

z is taken with a cut along the positive real axis,

then the domain D is transformed successively as follows:

z 7→ z

−−−−−−−−→

0−a

z 7→ z + a

−−−−−−−−→

z 7→

−−−−−−−−→

We can now deduce from this the ﬂow in D with the boundary condi-

tions

lim

Re(z)→±∞

v(z) = (v

∞

, 0).

In the general case, one can proceed as follows. Search for the ﬂow in the form

Ω(z) = v

∞

z + g(z),

where g is a hol omorphic function which describes a perturbation from the homogeneous ﬂow

Ω

(z) = v

∞

z, such that lim

|z|→∞

′

(z) = 0 so that the limit conditions are respected.

Applications to potential theory 169

After the conformal mapping w = f (z), the ﬂow still obeys the same

boundary conditions, since f

′

(z) ∼ 1 as |z| tends to inﬁnity in the upper

half-plane. The desired ﬂow in the upper half-plane without a wall is easy to

ﬁnd: it a a uniform ﬂow (the wind over the plain...), which can be described

by the complex potential

Θ(w) = v

∞

× w.

Coming back to the variable w:

Φ(z) = Θ(w) = Θ



+ a



= v

∞

+ a

Two special points appear: the velocity of the ﬂow is inﬁnite on the top of

the wall, at z = ia (this is why the wind “whistles” when going over a pointed

obstacle: locally supersonic velocities are reached); it is zero “at the foot of

the wall” (around z = 0). These two points are of course the two points

where the transformation is no longer conformal

; it is therefore possible that

singularities appear in this manner, which did not appear in the ﬂow on the

upper half-plane.

6.2.c Potential theory, lightning rods, and percolation

From the previous example we can understand the principle of th e lightning

rod. If we denote by ϕ( r) the electrostatic potential, then close to a pointed

object (like the wall above, or an acute angle in the deﬁnition of th e domain),

we can expect that ϕ

′

will diverge. Identifying C and R

, it is the gradient

of ϕ tha t will diverge, namely, the electric ﬁeld. But we know that in the air

an electric ﬁeld of intensity larger than some critical value, th e “breakdown

thresh old,” will cause a spont aneous electric discharge.

Saint Elmo’s ﬁre, well

known to mariners, has the same origin.

But this is not yet the most remarkable thing. Consider a problem of

random walk of a particle in an open domain Ω ⊂ C, assuming that, when the

particle meets the boundary of Ω, it will stop. (It is possible to make numerical

simulations of this problem.) Wha t will happen after many particles have

performed this process? One may think that the part icles will accumulate on

the boundary ∂Ω, which will therefore g row, more or less regularly as time

goes. I n fact, this is not what happens. If the boundary ∂Ω ha s “cusps, ”

they will att ract more particles and, hence, will grow faster than the rest of

the boundary. If, at a given time and due to t he effect of chance, a “cusp” is

created (by accumulation of some particles) on a “ smooth” part of ∂Ω, then

this cusp will, in turn, a ttract more particles. In a word: the ﬂuctuations of

the boundary become unst able.

Indeed, at t he foot of the wall, we have f

′

(z) = 0, whereas around the top, f

′

(z) diverges.

Of course, the rough explanation given only concerns ligh tning rods in a two-dimensional

world. In three dimensions, another argument must be found, because the one given uses

speciﬁc properties of C and not of R

170 Conformal maps

How to explain this phenomenon? If we denote by p(z, t) the probability

density for the particle to be at position z at time t, one can show that this

probability satisﬁes an equation of diffusion, which is the manifestation on a

macroscopic scale of the extremely erratic behavior of microscopic particles

(the so-called Brownian motion). The diffusion equation takes the form



∂

∂ t

−κ△



p(z, t) = 0

at any point of Ω. We will therefore have an equation of the same type if we

perform a conformal transformation (independent of time) on the domain Ω.

Once more, the cusps will attract more particles and we will observe a growth

phenomenon.

(Here it is the ﬂow of particles that diverges.)

6.3

Dirichlet problem and Poisson kernel

The Dirichlet problem is the following: the values of a harmonic function

on the boundary ∂Ω of a domain Ω in the plane are assumed to be known,

and we want to ﬁnd the values of the function at any point in Ω.

For instance, one may be interested in the case of a metallic disc,

which is

a h eat conductor, in a stationary state, for which we impose a temperature T

on one half-circle, and a temperature T

on the other half-circle. The question

is now to determine the temperature at any point inside the disc.

More precisely, if Ω is a domain (hence, a connected open set) of the

complex plane C, if ∂Ω denotes its boundary and if u

: ∂Ω → C is a

continuous function, we are looking for a u : Ω → C of C

class, such that

∂Ω

= u

△u = 0 in Ω.

A ﬁrst important case is when the d omain Ω is an open ball. Indeed,

according to Riemann’s mapping theorem, one can in principle reduce to this

case whenever Ω is homeomorphic to an open ball (and not the wh ole of C).

In this situation, we have a ﬁrst useful theorem:

THEOREM 6.21 Let u be a function harmonic on a neighborhood of B(0 ; 1). Then,

for any point a ∈ B(0 ; 1), we have

u(a) =

2π

u(e

iψ

)

1 −|a|



a −e

iψ



dψ.

In particular, fractal growth may be observed by a mechanism similar to this one.

Or, which amounts to the same thing, a metallic cylinder with inﬁnite length, on which

we assume translation invariance.

Dirichlet problem and Poisson kernel 171

Pe ter Gustav Lejeune- Dirichlet (1805—1859), German mathe-

matician, was professor successively in Breslau, Berlin, and Göt-

tingen, where he succeeded his teacher Gauss (see page 557). He

was also the brother-in-law of Jacobi and a friend of Fourier. He

studied trigonometric series and gave a condition for the conver-

gence of a Fourier series at a given point (see Theorem 9.46 on

page 268). His other works c oncern the theory of functions in

analysis and number theory.

To prove this theorem, we start by stating a technical lemma which tells us,

in s ub stance, “a nything that can be proved for the central point of the open

disc B(0 ; 1) can also be proved for an arbitrary point of the disc.”

LEMMA 6.22 Let a ∈ B(0 ; 1). Denote ϕ

(z)

def

z−a

1−az

. Then ϕ

∈ H (B

′

), wh ere

′

is some neighborhood of B(0 ; 1) (for instance B

′

= B(0 ; |a|

−1

)) and satisﬁes

i) ϕ

is bijective on B

′

;

ii) ϕ

B(0 ; 1)

is a bijection from B(0 ; 1) into itself;

iii) ϕ

−1

= ϕ

−a

;

iv) ϕ

(a) = 0.

In other words, ϕ

transforms the disc into itself, but moves the point a to the center in

a holomorphic manner.

Proof of Theorem 6.21. We use the mean value property for harmonic functions:

u(a) = u ◦ϕ

−a

(0) =

2π



−a

iθ

)



dθ =

2iπ

∂B



−a

(ζ )



dζ.

With the change of variable ξ = ϕ

−a

(ζ ), we obtain ζ = ϕ

(ξ),

dζ

dξ

= ϕ

′

(ξ) =

1 −|a|

(1 −

aξ )

and

u(a) =

2iπ

∂B

u(ξ )

(ξ)

′

(ξ) dξ =

2iπ

2π

u(e

iψ

)

1 −|a|

|a −e

iψ

dψ.

In Theorem 6.21, put a = r e

iθ

; there follows the equivalent formula:



r e

iθ



2π

u(e

iψ

) P (r, θ −ψ) dψ,

where P is the Poisson kernel:

172 Conformal maps

Siméon Denis Poisson (1781—1840) lost his father at ﬁfteen, and

was sent by his mothe r to study medicine in Paris to earn his

living. Seeing patients die under his care, he decided (accidentally,

having ﬁrst chosen the wrong classroom!) to dedicate himself to

mathematics. He was received ﬁrst at the École Polytechnique

at eighteen. Then honors came until the end of his life (he

was even made a baron by Louis XVIII). In mathematics, his

interests ranged over almost all of analysis: integration, Fourier

series, probability, and, especially, mathematical physics, celestial

mechanics and elect rostatics in particular. A member of the Royal

Council of Public Education, he tried to develop th e teaching of

mathematics.

DEFINITION 6.23 The Poisson kernel is the function P : [0, 1[×R → R

deﬁned by

P (r, θ) =

2π

1 − r

1 + r

−2r cos θ

2π

1 −r



r −e

iθ



Remark 6.24 In the case of holomorphic functions, the Cauchy formula not only reproduces

holomorphic functions, but also c reates them: if f is a given function on the circle C =

∂B(0 ; 1), assumed to be merely continuous, then

F (z)

def

2iπ

f (ζ )

ζ − z

dζ

is a holomorphic funct ion on B(0 ; 1).

However, there isn’t a very strong link between f and F , contrary to w h at one might

expect. For instance, for z

∈ C , nothi ng forces that f (z

) = lim

z→z

F (z). One may, for

instance, take f (z) = ¯z (which, by the way, coincides on the unit circle with the function

g(z) = 1/z). The preceding formula leads to F (z) = 0 for any z ∈ B (0 ; 1), as the reader can

amuse herself to prove.

On the other hand, for harmonic functions, there is a formula to create a harmonic

function from boundary values, with a continuity property, using the Poisson kernel. This is

the object of the next theorem.

THEOREM 6.25 (Dirichl et problem for a disc) Let f : ∂B(0 ; 1) → R be a

continuous function deﬁned on the unit circle. Put

u(z) =







2π

f (e

iψ

)

1 −|z|



z −e

iψ



dψ if z ∈ B(0 ; 1),

f (z) if z ∈ ∂B(0 ; 1).

Then u is continuous on B(0 ; 1) and har monic on B(0 ; 1).

If f is has discontinuities, then u is harmonic on B(0 ; 1) and continuous in each

point of the unit circle in which f happens to be continous.

Proof. The proof of this theorem is omitted. Still, we remark that it involves a

sequence of Dirac functions given by the Poisson kernel for [r → 1]. After reading

Dirichlet problem and Poisson kernel 173

−0,5

0,5

−1

−0,5

0,5

−1

−0,5

0,5

Fig. 6.5 — The temperature is equal to −1 on the lower half-circle, and to +1 on the upper

half-circle; it is a harmonic function on the disc. Here it is represented on the

vertical axis, and is deduced from the preceding th eorem.

chapter 8 on distributions, and in particular section 8.2.b on page 231, the reader is

invited to try to formalize the proof of this theorem.

The Dirichlet problem has many applications in physics. Indeed, t here are

many equations of “harmonic” type: electromagnetism, hydrodynamics, heat

theory, and so on. The example already mentioned — ﬁnd the temperature at

any point in a disc where the temperature is imposed to be T

on the upper

half-circle and T

on the lower half-circle — is illustrated in Figure 6.5. After

integration, one ﬁnds (in polar coordinates)

T (r, θ) =

arctan



2r sin θ

1 −r



In Exercises 6.7 and 6.8, two other examples of solutions of the Dirichlet

problem are given, for a half-plane and for a strip, respectively.

174 Conformal maps

EXERCISES

 Exercise 6.1 Let U : R

→ R

be a twice differentiable function. Show that if f : C → C is

holomorphic, then denoting f : (x + i y) 7→ (X + i Y ), we have

△

(x, y)

U (x, y) =



′

(x + i y)



△

(X ,Y )

U (X , Y ),

with

U (X , Y )

def

= U ◦ f

−1

(X , Y ).

 Exercise 6.2 Show that any two annuli are homeomorphic (one can use, for instance, a

purely radial function).

Complex ﬂows

 Exercise 6.3 Determine the ﬂow of the wind in a two-dimensional domain delimited by two

half-lines meeting at an ang l e α (for instance, one of the half-lines represents the horizontal

ground, and the other a mountainside wit h uniform slope). Use the following boundary

conditions: the wind must have velocity with modulus v and ﬂow parallel to the boundaries,

inﬁnitely far away from the intersection of the lines.

Assume that the ﬂow is irrotational, incompressible, and stationary. In p articular, what is

the velocity of the wind at the point where the slope changes? C onsider the various possibilities

depending on the value of α ∈ [0, π].

 Exercise 6.4 Let k be a real number. Interpret the c omplex ﬂows given by

Ω

(z) = k log(z −a) and Ω

(z) = ik log(z −a).

 Exercise 6.5 We wish to solve the problem of the ﬂow of a Newtonian ﬂuid i n three dimen-

sions around a cylinder with inﬁnite length and circular section. If only the solutions which

are invariant by translation along the axis are sought, the p roblem is reduced to t h e study of

the ﬂow of a ﬂuid in two dimensions around a disc.

We assume that the velocity of the ﬂuid, far from the obstacle, is uniform. We look for

the solution as a complex potential Φ written in the form

Φ = V

z + G(z),

where the term V

z is the solution unperturbed by the disc and where G(z) is a perturbation,

such that

′

(z) −−−−→

|z|→+∞

Check that the solution obtained is indeed compatible with the boundary conditions (the

velocity of the ﬂuid is tangent to the disc), and ﬁnd the stagnation points of the ﬂuid.

Exercises 175

Dirichlet pro blem

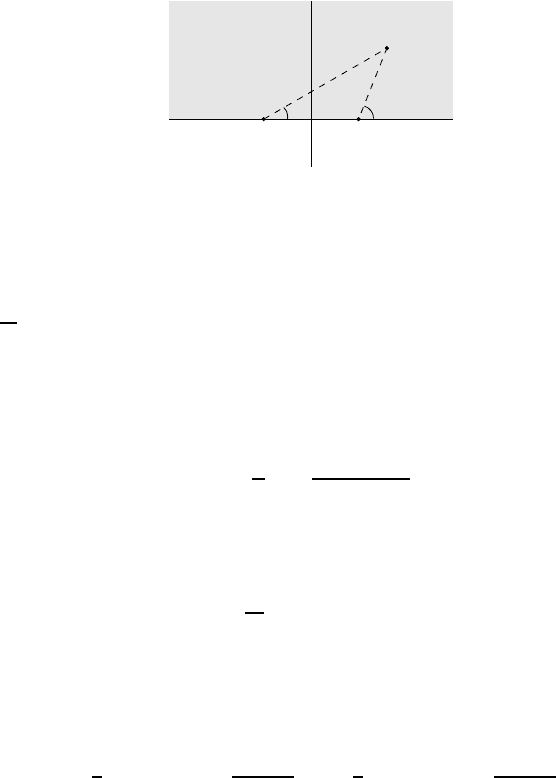
 Exercise 6.6 We wish to know the temperature of a sheet in the shape of an inﬁnite half-

plane, represented in the complex plane by the clo se d region

D = {z ∈ C ; Im(z) ¾ 0}.

We assume that the temperature on the boundary of the sheet is given by

T (x) =







if x < −1,

if |x| < 1,

if x > 1.

If z ∈ D, we denote by θ

and θ

the angles deﬁned in the picture below:

−1 1

Show th at any function z 7→ αθ

+ βθ

+ γ (with α, β, γ ∈ R) is harmonic. Deduce from

this the solution to the Dirichlet problem.

 Exercise 6.7 Dirichlet problem for a half-plane: consider the domain

D = {z ∈ C ; Imz > 0}.

We want to ﬁnd u of C

class deﬁned on D with values in R, admitting a continuous extension

to D and such t h at

△u = 0 in D,

|∂D

= u

given.

Find, using the Cauchy formula, an integral formula for u(z) when Imz > 0.

Hint: Show, before concluding, that if z = x + i y with y > 0 and if f is holomorphic

on D, then

f (z) =

+∞

−∞

y f (η)

(η − x)

+ y

dη.

 Exercise 6.8 Dirichlet problem for a strip: we are seeking th e solution of the Dirichlet

problem for a strip

B = {z ∈ C ; 0 < Imz < 1}.

In other words, we are looking for a function u of C

class deﬁned on B with values in R,

admitting a continuous extension to B, and such that







△u = 0 in B,

u(x) = u

(x) ∀x ∈ R,

u(x + i) = u

(x) ∀x ∈ R.

Show that if u

def

= Re f (with f holomorphic) is a solution of the problem, then we have

f (z) =

+∞

−∞

(t) coth



π(t − z)



dt +

+∞

−∞

(t) tanh



π(t − z)



dt.

176 Conformal maps

SOLUTIONS

 Solution of exercise 6 .2. Writing as usual z = re

iθ

and denoting by r

< r < r

the ﬁrst

annulus and by r

′

< r < r

′

the second one, consider t h e map







r 7−→



′

− r

′

− r



(r −r

) + r

′

θ 7−→ θ.

This application is indeed an homeomorphism from the ﬁrst annulus onto the second (the

transformation of the radius is afﬁne). One can check that this is not a holomorphic map,

except if the two annuli are homothet ic to each other, in which case the formula given is the

corresponding homothety.

 Solution of exercise 6 .3. We can transform t h e domain D into the upper half-plane by

means of t h e following conformal map:

z 7−→ w = z

π/α

In the domain D

′

= {z ∈ C ; Im(z) > 0}, the ﬂow of the wind is gi ven by a complex potential

Θ(w) = vw; one checks indeed that the velocity ﬁeld that deri ves from t his is uniform and

parallel to the ground (since v ∈ R). The function Θ being holomorphic, its real part ReΘ,

which is the real velocity potential, is harmonic: △(ReΘ) = 0. Coming back to the initial

domain, we put

Φ(z) = Θ



w(z)



= Θ



π/α



= v × z

π/α

which therefore satisﬁes △(ReΦ



= 0 (because of Corollary 6.15) and has the required bound-

ary conditions. The velocity of he wind is given by the gradient of ReΦ.

At z = 0, the mapping z 7→ w is not conformal. If α < π, the derivative

π/α−1

tends to 0 (and so does t h e velocity of the wind), which shows that at the bottom of a V-

shaped valley one is protected from the transversal wind (but not from the longitudinal wind,

as people from Lyons know, who are victim of the North-South wi nd, whereas the East-West

wind is almost absent). On the other hand, if α > π, this derivative tends to inﬁnity, which

shows that on the c rest of a mountain, the transverse wind is important.

 Solution of exercise 6 .4. Ω

corresponds to the ﬂow around a source or a sink (depending

on the sign of k), and Ω

corresponds to a whirlpool, as one can see by picturing the velocity

ﬁeld.

 Solution of exercise 6 .5. Rotating t h e entire system if necessary, we may assume that the

velocity at inﬁnity is p arallel to the real axis. Therefore we take V

∈ R and look for a ﬂow

symmetric with respect to the real axi s.

We know a conformal transformation that maps the half-plane minus a half-disc into the

upper half-plane; it is given by z = z + a

/z, where a is the radius of the disc t h at is removed.

The circle C (0 ;a) is mapped to the segment [−2a, 2a].

There only remains to ﬁnd a free ﬂow in the new domain: it is given trivially by

Θ(w) = V

The solution of the problem is therefore

Φ(z) = V



z +

