Appel W. Mathematics for Physics and Physicists

Подождите немного. Документ загружается.

Dirac and its derivatives 197

Remark 7.40 This expression requires a notion of convergence in the space D

′

, which will be

introduced in Section 8.2.a on page 23 0 .

Can this be generalized to the three-dimensional case? In that situation, we

cannot simply take the derivative, but we must indicate the direction in which

to d ifferentiate.

DEFINITION 7.41 In R

, th e distributions δ

′

, δ

′

, and δ

′

, are deﬁned by



′

, ϕ



def

= −ϕ

′

(0) = −

∂ϕ

∂ x

(0),



′

, ϕ



= −ϕ

′

(0) = −

∂ϕ

∂ y

(0),



′

, ϕ



= −ϕ

′

(0) = −

∂ϕ

∂ z

(0).

We denote by δ

′

the vector (δ

′

, δ

′

, δ

′

Let’s use these results to compute the electrostatic potential c reated by an elecrostatic

dipole. The potential created a t a point s by a regular distribution of charges ρ

V ( s) =

4πǫ

ZZZ

ρ( r)

kr − sk

which can be written

V ( s) =

4πǫ



ρ( r),

kr − sk



Now we extend t his relation to other types of distributions, such as point-like,

curvilinear, surface, or dipolar distributions.

PROPOSITION 7.42 The potential created at a point s by the distribution of

charges ρ( r) is

V ( s) =

4πǫ



ρ( r),

kr − sk



. (7.4)

Remark 7.43 The function s 7→ 1/ kr − sk is not of C

∞

class, nor with bounded support.

As far as the support is concerned, we can work around the problem by imposing a

sufﬁciently fast decay at inﬁnity of the distribution of charges. For the problem of the

singularity of 1/ kr − sk at s = r , we note that the function still remains integrable since the

volume element is r

sin θ dr dθ dϕ; this is enough for the e xpression (7.4) to make sense in

the case of most distributions ρ of physical interest.

Consider now the dipolar distribution

T = −δ

′

· P = −P

′

− P

′

− P

′

198 Distributions I

where we have denoted by P the dipole moment of the source. Then the

potential is given by

V ( s) =



T ( r),

kr − sk





−P

′

− P

′

− P

′

kr − sk





∂

∂ x

kr − sk

+ P

∂

∂ y

kr − sk

+ P

∂

∂ z

kr − sk



r=0

namely,

V ( s) = P

ksk

+ P

ksk

+ P

ksk

P · s

ksk

which is consistent wit h the result expected [50, p. 138].

THEOREM 7.44 In the usual space R

, an electrostatic dipole with dipole moment

equal to P is described by the distribution −δ

′

· P .

 Exercise 7.2 Show that, in dimension one, dilating δ

′

by a factor a 6= 0 yields

′

(ax) =

a |a|

′

(x)

(Solution page 245)

7.4.d Composition of δ with a function

The goal of this section is to give a meaning to the distribution δ



f (x)



where f is a “sufﬁciently regular” function. This amounts to a change of

variable in a distribution and is therefore a generalization of the notions of

translation, dilation, and transposition.

Consider ﬁ rst the special case of a regular distribution and a change of

variable f : R → R which is differentiable and bijective.

Let g be a locally integrable function. The function g ◦ f being still locally

integrable, it deﬁnes a distribution a nd we have

〈g ◦ f , ϕ〉 =



f (x)



ϕ(x) dx =

g( y) ϕ



−1

( y)





′



−1

( y)





since, in the substitution y = f (x), t he absolute value of the ja cob ian is equal



′

(x)



′



−1

( y)





By analogy, for a distribution T , we are led to deﬁne t he distribution T ◦ f

as follows:

〈T ◦ f , ϕ〉

def



′

◦ f

−1



, ϕ ◦ f

−1

Dirac and its derivatives 199

Thus, the distribution δ



f (x)



satisﬁes





f (x)



, ϕ





′

◦ f

−1



, ϕ ◦ f

−1



−1

(0)





′



−1

(0)





for any ϕ ∈ D, wh ich can also be written



f (x)





′

( y

)



δ( y − y

where y

is the unique real number such that f ( y

) = 0. Note that it is

necessary that f

′

( y

) 6= 0: the function f must not vanish at the same time

as its derivative.

We can then generalize to the case of a function f not necessa rily bijective

— but still differentiable — by wr iting (within quotes!)

〈δ ◦ f , ϕ〉 =

“

+∞

−∞



f (x)



ϕ(x) dx

”

x |f (x)=0



′

(x)



ϕ(x).

To summarize:

THEOREM 7.45 Let f be a dif ferentiable function which has only isolated zeros.

Denote by Z( f ) the set of these zeros: Z( f ) = {y ∈ R ; f ( y) = 0}. Assume that

the derivative f

′

of f does not vanish at any of the points in Z( f ). Then we have



f (x)



y∈Z( f )



′

( y)



δ(x − y).

A classical application of this result to special relativity is proposed in Exer-

cise 8.9 on page 242.

7.4.e Charge and current densities

In this s ection, we study the application of the preceding change of variable

formula, in a s imple physical situation: the Lorentz transformation of a cur-

rent four-vector.

In electromagnetism, the state of th e system of charges is described by d ata

consisting of

• the charge density ( x, t) 7→ ρ( x, t) ;

• the current density ( x, t) 7→ j( x, t).

In the case of a point-like particle with charge q, if we denote by t 7→ R(t) its

position and by t 7→ V (t) its velocity, wit h V (t) = dR(t)/dt, these densities

are given by

ρ( x, t) = q δ

(3)



x − R(t)



and j ( x, t) = q V (t) δ

(3)



x − R(t)



200 Distributions I

Moreover, the densit ies of charge and current form, from the point of

view of special relativity, a four-vector. In order to distinguish them, we will

denote three-dimensional vectors in the form “ j ” and four-vectors in the form

“j = (ρ, j/c)”.

During a change of Galilean reference frame, characterized by a velocity

v (or, in nondimensional form, ββ

ββ = v/c), these quantities are transformed

according to the rule

(ρ

′

, j

′

/c) = Λ(ββ

ββ) ·(ρ, j/c), i.e., j

′

= Λ(ββ

ββ) ·j with j

def

= (ρ, j/c), (7.5)

where Λ(ββ

ββ) is the matrix characterizing a Lorentz transformation. To simplify,

we consider the case of a Lorentz transformation along the axis (Ox), cha r-

acterized by th e velocity ββ

ββ = βe

. Denote by x = (c t, x) = (x

, x

)

the coordinates in the original reference frame R and by x

′

= (c t

′

, x

′

) =

′0

, x

′1

, x

′2

, x

′3

) the coordinates in the reference frame R

′

with velocity ββ

ββ

relative to R. The Lorentz transformation of the coordinates is then given by







c t

′













γ −βγ

−βγ γ













c t







, with γ

def

1 −β

which we will w rite

as x

′

= Λ(ββ

ββ) ·x. Expanding, we ob tain











′

= γ t −γβx/c = γ(t − vx/c

′

= −γβc t + γ x = γ(x −vt),

′

= y,

′

= z,

and











t = γ(t

′

+ vx

′

x = γ(x

′

+ vt

′

y = y

′

z = z

′

Although it is almost always written in the form (7.5), the transformation

law of the current four-vector is more precisely given by

j(x

′

) = Λ(ββ

ββ) ·j



Λ(ββ

ββ)

−1

·x

′



= Λ(ββ

ββ) ·j(x),

or, in the case under consideration

′

( x

′

, t) = γ



ρ( x, t) −

β j

( x, t)



, j

′

( x

′

, t) = γ



( x, t) − cβρ( x, t)



(7.6)

The case of a particle at rest

Consider a simple case to begin with, where the particle is at rest in the

laboratory reference frame R.

Of course, tensorial notation can also be use d to write x

′µ

= Λ

Derivation of a discontinuous func tion 201

Then j(x) = q



(3)

( x), 0



. Looking back at equation (7.6), and denoting

by L

−1

( x

′

) = γ(x

′

+ vt

′

) the spacial part of the inverse transformation

Λ(ββ

ββ)

−1

, we obtain



′

( x

′

, t),

′

( x

′

, t

′

)



= q



γ δ

(3)



−1

( x)



, −ββ

ββγ δ

(3)



−1

( x

′

)





Notice then that

γ δ

(3)



−1

( x

′

)



= γ δ

(3)



γ(x

′

+ vt

′

), y

′

, z

′



= γ δ



γ(x

′

+ vt

′

)



δ( y

′

) δ(z

′

)

= δ(x

′

+ vt

′

) δ( y

′

) δ(z

′

) (change of variable)

= δ

(3)

( x

′

+ vt)

which gives, as might be expected

′

( x

′

, t

′

) = q δ

(3)

( x

′

+ vt), j

′

( x

′

, t) = −q v δ

(3)

( x

′

+ vt).

So we see that the Dirac distribution has some kind of invar iance property

with respect to Lorentz transformations: it does not acquire a “factor γ,”

contrary to what equation (7. 6) could suggest. This is a happy fact, since the

total charge in space is given by

′

ZZZ

′

( x

′

, t) d

′

= q,

and not γq!

This result generalizes of course to the case of a particle with an ar bitrary

motion compatible with special relativit y.

7.5

Derivation of a discontinuous function

7.5.a Derivation of a function di scontinuous at a point

We saw that any locally integrable function is differentiable in the sense of

distributions. Hence, we can differentiate the Heaviside function and ﬁnd

that H

′

= δ. If we had taken the derivative of H in t he usual sense of

functions, we would have obtained a function zero everywhere except at 0,

where it is not deﬁned. A primitive of this derivative would then have given

the zero function, not H .

In other words, the following diagram cannot be “closed”:

function H

derivation

−−−−−→ 0



no!



distribution H

derivation

−−−−−→ δ

202 Distributions I

The same will happen for any function with an isolated discontinuity at a

point: its derivative will exist in the sense of distributions, wh ich differs from

the usual derivative (if it exists) by a Dirac peak with height equal to the jump

of the function.

The following notation will be used:

• f is the function being studied, or its as sociated distribution;

•



′



will be the regular distribution ass ociated to the usual derivative

of f in the sense of functions:



′



, ϕ



+∞

−∞

′

(x) ϕ(x) dx ;

this is of course a distribution; the derivative of f in the sense of

functions is a function which is not deﬁned everywhere (in particular,

it is not at the points of discontinuity of f ), but the associated regular

distribution is well-deﬁned a s long as f

′

is deﬁned almost everywhere (and

locally integrable);

• f

′

will be the derivative of the distribution f , deﬁned as above by



′

, ϕ



= −



f , ϕ

′



;

this is also a distribution.

Example 7.46 With this notation, the derivative in the sense of distributions of the Heaviside

distribution H is H

′

= δ, but t he distribution associated to the derivative of H taken in the

sense of functions is



′



= 0.

Let f be a function which is piecewise of C

class. Denote by a

the

points of discontinuity of f (we assume there are ﬁnitely many) and by σ

(0)

the jump of f at a

: σ

(0)

= f (a

) − f (a

−

). One can then write f as th e sum

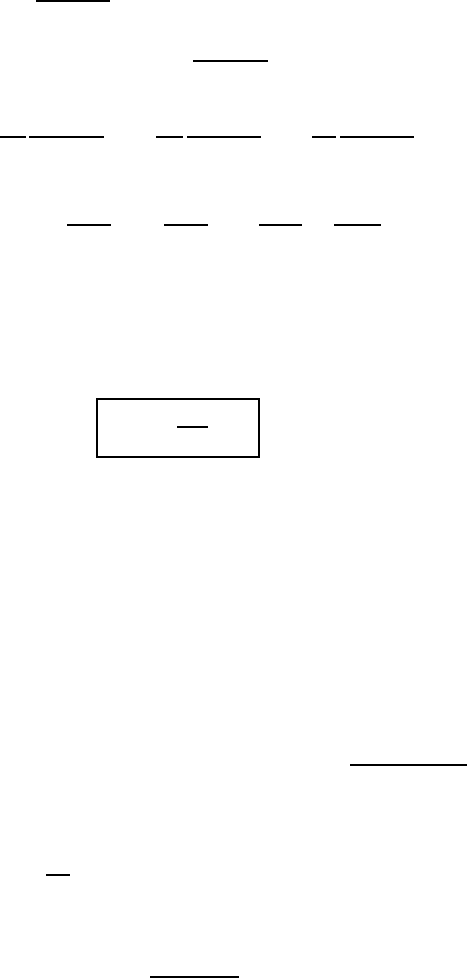
of a continuous f unction g and multiples of Heaviside functions (see Figure 7.2

on the next page):

f (x) = g(x) +

(0)

H (x − a

Since the usual derivatives of the functions f and g are equal almost every-

where, we have



′



= {g

′

}. However, remembering that H

′

= δ, we obtain,

in the sense of distributions

THEOREM 7.47 (Derivative of a discontinuous function) Let f be a function

which is piecewise C

. Then, with the notation above, we have

′



′



(0)

δ(x − a

). (7.7)

Derivation of a discontinuous func tion 203

(0)

Fig. 7.2 — Example of a function with a discontinuity at a with ju mp equal to σ

(0)

To lighten th e notation, we will henceforth write equation (7.7) more com-

pactly as follows:

′



′



+ σ

(0)

δ ;

all the d iscontinuities of f are implicitly taken into a ccount. Similarly, if we

denote by σ

(1)

any d iscontinuity of the derivative of the function f , σ

(2)

any discontinuity of its second d erivative, and so on, then we will have the

following result, with similar conventions:

THEOREM 7.48 (Successive derivatives of a piecewise CC

∞

function) Let f be

a piecewise C

∞

function. Then we have

′′



′′



+ σ

(1)

δ + σ

(0)

′

and more generally

(m)

+ σ

(m−1)

δ + ···+ σ

(0)

(m−1)

∀m ∈ N.

Example 7.49 Consider the function E : x 7→ E(x) = “integral part of x.” Then



′



= 0,

whereas, in the sense of distributions, we have E

′

= X.

 Exercise 7.3 Compute the successive derivatives of the function f : x 7→ |x|.

◊ Solution: Since f is continuous, i ts derivative in the sense of distributions

is the distribution associated to its usual derivative. But the derivative of f is

the function x 7→ sgn(x) for any x 6= 0, which is deﬁned everywhere e xcept at

x = 0. The associated regular distribution, denoted



′



, is the distribution

“sgn(x)” (meaning “sign of x”) deﬁned by



sgn(x), ϕ(x)



+∞



ϕ(x) −ϕ(−x)



dx.

Therefore, the derivative of f in the sense of distributions is f

′



′



= sgn.

The function x 7→ sgn(x) has a discontinuity at 0 with jump equal to 2.

Moreover, i ts usual derivative is zero almost e verywhere (it is undeﬁned at 0

and zero everywhere else), which shows that

{sgn

′

} = 0 and f

′′

= sgn

′

= 2δ.

We deduce that the next derivatives of f are given by

(k)

= 2δ

(k−2)

for any k ¾ 2.

204 Distributions I

7.5.b Derivative of a function with discontinuity

along a surface SS

Let S be a smooth surface in R

, and let f : R

→ C be a f unction which is

piecewise of C

class, with a discontinuity along the surface S .

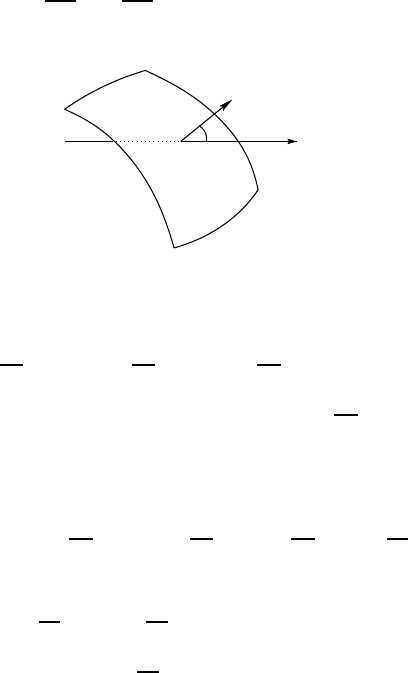
We denote by x

= x, x

= y, and x

= z the coordinates and assume the

surface S is oriented. For i = 1, 2, 3, we denote by θ

the angle between the

exterior normal n to the surface S and the axis (O x

). Arguing as in the

previous section, the following theorem will follow:

THEOREM 7.50 (Derivatives of a function discontinuous along a surface) Let

f be a function with a discontinuity along the surface S . Denoting by σ

(0)

the “jump”

function S , equal to the value of f just outside minus the value just insid e, we have

∂ f

∂ x



∂ f

∂ x



+ σ

(0)

cos θ

. (7.8)

Proof. Assume that f is of class C

on R

\S and that its ﬁrst derivatives admit

a limit on each side of S . We now evaluate the action of ∂ f /∂ x on an arbitrary test

function ϕ ∈ D(R



∂ f

∂ x

, ϕ



= −



f ,

∂ϕ

∂ x



= −

ZZZ

∂ϕ

∂ x

dx dy dz

= −

ZZZ

f (x, y, z)

∂ϕ

∂ x



dy dz

for a smooth surface. Fix now y

∗

and z

∗

and denote by x

∗

the real number such that

∗

, y

∗

, z

∗

) ∈ S (generalizing to the case where more than one real number satisﬁes

this property is straightforward). In addition, put h(x) = f (x, y

∗

, z

∗

). Then we have

f (x, y

∗

, z

∗

)

∂ϕ

∂ x

dx =

h(x)

∂ϕ

∂ x

dx =



∂ϕ

∂ x



= −



∂ h

∂ x

, ϕ



and we can now use Theorem 7.47, which gives



∂ h

∂ x

, ϕ





∂ h

∂ x



+ σ

(0)

∗

, y

∗

, z

∗

) δ(x − x

∗

), ϕ



∂ h

∂ x

ϕ dx + σ

(0)

∗

, y

∗

, z

∗

) ϕ(x

∗

, y

∗

, z

∗

where we have denoted by σ

(0)

∗

, y

∗

, z

∗

) the jump of f across the surface S at the

point (x

∗

, y

∗

, z

∗

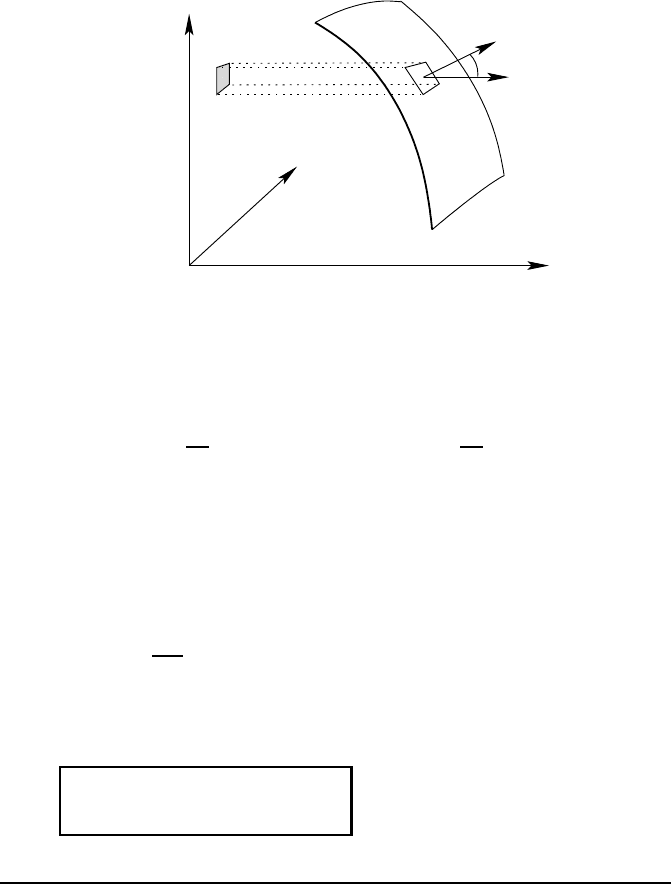
Derivation of a discontinuous func tion 205

But, integrating now with respect to y

∗

and z

∗

, we remark that

(0)

ϕ dy dz =

(0)

ϕ cos θ

since d

s cos θ

= dy dy, as can be seen i n the ﬁgure.

dx dy

To conclude, we write

(0)

ϕ cos θ

s =



(0)

cos θ

, ϕ



Putting these results together, we obt ain



∂ f

∂ x

, ϕ





(0)

cos θ

, ϕ



ZZZ

∂ f

∂ x

ϕ dx dy dz

for any ϕ ∈ D(R

). The same arg u ment performed w ith the partial derivatives with

respect to y or z leads to the stated formula (7.8).

Now we apply this result to a function f differentiable in a volume V

delimitied by a closed surface S = ∂V , and equal to zero outside this volume.

Taking the test function ϕ(x) ≡ 1, we get

ZZZ

∂ f

∂ x

dv −

f cos θ

ds = 0 for i = 1, 2, 3,

or, combining the three formulas for i = 1, 2, 3 in vector form, and noticing

that n = (cos θ

, cos θ

)

ZZZ

grad f d

v =

f n d

s Green-Ostrogradski formula.

More precisely, we should take a test function ϕ equal to 1 on V , but wit h bounded

support. If V is bounded, such a function always exists.

206 Distributions I

The formula (7.8) may also be applied to the components of a vector

function f = ( f

, f

); then, after summing over indices, we get

ZZZ

∂ f

∂ x

v −

cos θ

s = 0,

or equivalently

ZZZ

div f d

v =

( f · n) d

s Green-Ostrogradski formula.

7.5.c Laplacian of a func tion discontinuous

along a surface SS

By applying the results of the previous section, it is possible to compute, in

the sense of distribut ions, the laplacian of a function which is discontinuous

along a smooth surface.

THEOREM 7.51 (Laplacian of a discontinuous function) Let S be a smooth

surface and f a function of C

∞

class except on the surface S . D enote by σ

(0)

the

“jump” of f across the surface S . Denote moreover by

∂ f

∂ n

the derivative of f in the

normal direction n, deﬁned by

∂ f

∂ n

def

∂ f

∂ x

cos θ

= (grad f ) · n,

and let σ

(1)

be the jump of this function. Th en we have

△f = σ

(0)

′

+ σ

(1)

+ {△f }, (7.9)

where δ

′

is the normal derivative of δ: δ

′

cos θ

= δ

′

· n.

Remark 7.52 The action of the distribution δ

′

on any test function ϕ is therefore gi ven by

〈δ

′

, ϕ〉 = −



∂ϕ

∂ n



THEOREM 7.53 (Gr een formula) Let f be a function twice differentiable in a

volume V bounded by a surface S , and let ϕ be a test function. Denoting by n the

exterior normal to S , we h ave

ZZZ

( f △ϕ −ϕ △ f ) d

v =



∂ϕ

∂ n

−ϕ

∂ f

∂ n



s. (7.10)

Proof. Extend f by putting f ( r ) = 0 for any point out side V .

Note that the jump of f accross the surface S at a point r is −f ( r) when crossing

in the exterior direction, and similarly for the other jump functions involved.