Appel W. Mathematics for Physics and Physicists

Подождите немного. Документ загружается.

Physical interpretation of convolution operators 217

(if this expression makes sense), where krk denotes, with a slight abuse of

notation, the f unction r 7→ krk. I t is then easy to compute, in the sense of

distributions, the laplacian of the potential. Indeed, it sufﬁces to compute th e

laplacian of one of the two factors in this convolution. Since we know that

△(1/r) = −4πδ, we obtain

△V =

4πǫ

△



ρ ∗

krk



4πǫ



ρ ∗△

krk



4πǫ

ρ ∗(−4πδ)

= −

Thus we have recovered a classical result:

THEOREM 7.77 (Poisson equation) The la placian of the electrostatic potential cre-

ated by a distribution of charge ρ is

△V = −

7.7

Physical interpretation of convolution operators

We are going to see now t hat many physical systems, in particular mea-

suring equipment can be represented by convolution operators. Suppose we

have given a physical system which, when excited by a n input signal E de-

pending on time, produces an output signal, denoted S = O (E). We make

the assumptions that the operator O that transforms E into S is

• linear;

• continuous;

• invariant under translations, that is, the following diag ram commutes

(this means that composing the arrows from the upper left corner to

the bottom right corner in the two possible ways has the same result):

E(t)

−−−→ S(t)

translation



translation

E(t − a)

−−−→ S (t −a)

218 Distributions I

THEOREM 7.78 If the three conditions stated above h old, then the operator O is a

convolution operator, that is, there exists R ∈ D

′

such that

S = O(E) = E ∗R = R ∗ E

for any E.

The converse is of course true.

Remark 7.79 The case of an excitation depe nding on time is very simple. If, on the other

hand, we consider an optical system where the source is an exterior object and where the

output is measured on a photo-detector, the variable corresponding to the measurement (the

coordinates, in centimeters, on the photographic plate) and the variable corresponding to the

source (for instance, th e angular co ordinates of a celestial object) are diffent. One must then

perform a change of variable to be able to write a convolution relation between the input and

output signals.

Knowing the distribution R makes it possib le to predict the response of

the system to an arbitary excitation. The distribution R is called the impulse

response because it corresponds to the output to an elementary δ input:

−→ O(δ) = δ ∗ R = R.

Note that often, in physics, the operator linking S (t) and E(t) is a differ-

ential operator.

One can then write D ∗ S = E where D is a distribut ion

which is a combination of derivatives of the unit δ.

The distribution R,

being the output corresponding to a Dirac peak, therefore satisﬁes

R ∗ D (t) = D ∗ R (t) = δ(t)

|{z}

E(t)

Since δ is the neutral element for the convolution, the distribution R is

thus the inverse of D for the convolution product. This point of view is

developed in Section 8.4 on page 238. I n general, this operator D is given

by physical considerations; we will describe below the technique of Green

functions (Chapter 15), where the purely technical difﬁculty is to compute, if

it exists, the convolution inverse of D.

Remark 7.80 Experimentally, it is not always easy to send a Dirac function as input. It is

doable in optics (use a star), but rather delicate in electricity. It is sometimes simpler to send

a signal close to a Heaviside function. The response to such an excitation, which is called the

step response, is then S = H ∗R. If we differentiate this, we obtain S

′

= H

′

∗R = δ ∗R = R,

which shows the following result:

THEOREM 7.81 The impulse response is the derivative of the step response.

Consider, for instance, a particle with mass m and position x(t) on the real axis, subject

to a force depending only of time F (t). Take, for example, the excitation E(t) =

F (t) and

the response S(t) = x(t). The evolution equation of the system is S

′′

(t) = E(t).

In the previous example, one can t ake D = δ

′′

, since δ

′′

∗ S = S

′′

Physical interpretation of convolution operators 219

A window

Two stars

through the telescope

A star

Fig. 7.3 — Some objects to look at with a telescope.

If T is sufﬁciently smooth, this differentiation can be performed numerically; however, differ-

entiation is often hard to implement numerically. This is the price to pay.

DEFINITION 7.82 (Causal system) A system represented by a temporal con-

volution operator (i. e. , by a t ime variable) is called a causal system if its

impulse response R(t) is zero on R

∗−

(which means that 〈R, ϕ〉 = 0 for any

test f unction ϕ which is zero for t ¾ 0).

In a causal system, the effect of a signal cannot come before its cause

(which is usually expected in physics).

Example 7.83 (in optics) Look at the sky with a telescop e. Each star is a point-like li ght

source, modeled by a Dirac δ. Represent the light intensity of a star centered in the telescope

by a distribution aδ; then the image of this star after passing through the telescope is given

by a function of the intensity aψ(x, y), showing the diffraction spot due to the ﬁnite size of

the mirror and to the Newton rings.

Any incoherent luminous object (which is indispensable

to ensure linearity with respect to th e light intensity functions), with intensity function i n the

coordinates (x, y) equal to F (x, y), will give an image F (x, y) ∗ψ(x, y) (see Figure 7.3).

The function ψ is studied in Chapter 11, page 320.

220 Distributions I

7.8

Discrete convolution

It should be noted that it is quite possible to deﬁne a discrete convolution

to model the “fuzziness” of a d igitalized picture. Such a picture is given no

longer by a continuous function, but by a sequence of values n 7→ x

with n ∈

[[1, N ]] (in one dimension) or (m, n) 7→ x

m n

with (m, n ) ∈ [[1, N ]] × [[1, M]]

(in two dimensions). Each of these discrete numerical values deﬁnes a pixel.

In t he one-dimensional case, we are given values α

for n ∈ [[1, N ]] (and

we put α

= 0 outside of this interval), and the convolution is deﬁned by

y = α ∗ x with y

+∞

k=−∞

n−k

the support of y being then equal to [[1 − M , N + M ]]. In two dimensions,

the corresponding formula is

y = α ∗ x with y

m n

+∞

k=−∞

+∞

ℓ=−∞

kℓ

m −k,n−ℓ

Photo-processing softwares (such as Photoshop, or the GIMP, w hich is Free —

as in Free Speech — software) provide such convolutions. An example of the

result is given in Figure 7.4 on the facing page.

The dis crete convolution may be written as a matrix operation, with the

advantages and inconveniences of such a representation. Th e inversion of this

operation is done with the inverse matrix when it exists. We refer the reader

desirous to learn more to a book about signal t heory.

—

The exercises for this chapter are found at the end of Chapter 8, page 241.

Discrete c onvolution 221

Fig. 7.4 — A square in Prague, before and after discrete convolution.

Laurent Schwartz, born in Paris in 1915, son of the ﬁrst Jewish surgeon in the

Paris hospitals, grandson of a rabbi, was a student at the École Normale Supérieure.

During World War II, he went to Toulouse and then to Clermont-Ferrand, before

ﬂeeing to Grenoble in 1943. I n 1944, he barely escaped a German raid. After the war,

he taught at th e University of Nancy, where the main part of the Bourbaki group

was located. He came back to Paris in 1953 and obtained a position at the École

Polytechnique in 1959.

He worked in partic u lar in functional analysis (under the inﬂucence of

Dieudonné) and, in 1944, created the theory of distributions. Because of th ese

tremendously important works, he was awarded the Fields M edal in 1 950. He showed

how to use this theory in a physical context.

Finally, one cannot omit, side by side with the mathematician, the political mili-

tant, the paciﬁst, who raised his voice against the crimes of the French state during

the Algerian war and fought for the independence of Algeria [82].

Laurent Schwartz passed away on July 4, 2002.

Chapter

Distributions II

In this chapter, we will ﬁrst discuss in det ail a particular distribution which is very

useful in physics: the “Cauchy principal value” distribution. Notably, we will derive

the famous formula

x ± iǫ

= pv

∓iπδ,

which appears in optics, statistical mechanics, and quantum mechanics, as well as

in ﬁeld theory. We will also treat the topology on t h e space of distributio ns and

introduce the notion of convolution algebra, which will lead us to t h e notion of

Green function. Finally, we will show how to solve in one stroke a differential

equation wi th the consideration of initial conditions for the solution.

8.1

Cauchy principal value

8.1.a Deﬁnition

The function x 7→

does not deﬁ ne a regular distribution, since it is not

integrable in the neighborhood of x = 0. On the other hand, one can deﬁne,

for ϕ ∈ D(R), the limit

+∞

−∞

ϕ(x)

def

= lim

ǫ→0

|x|¾ǫ

ϕ(x)

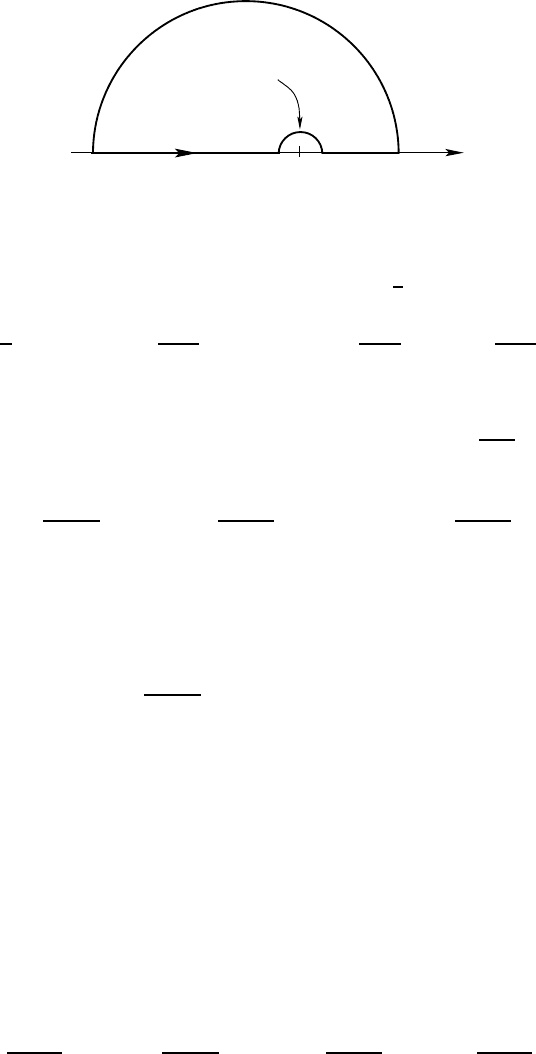
224 Distributions II

(ǫ)

Fig. 8.1 — The contour γ

which provides the deﬁnition of the distribution pv

, given by



, ϕ

= pv

+∞

−∞

ϕ(x)

def

= lim

ǫ→0

Z

−ǫ

−∞

ϕ(x)

dx +

∞

ϕ(x)



This is then generalized as follows:

DEFINITION 8.1 Let x

∈ R. T he Cauchy principal value pv

x−x

is deﬁned

as the distribution on R given by



x − x

, ϕ



= pv

ϕ(x)

x − x

def

= lim

ǫ→0

x−x

|>ǫ

ϕ(x)

x − x

dx.

8.1.b Application to the c omputation of certain integrals

The situation that we are considering is the computation of an integral of the

type

+∞

−∞

f (x)

x − x

dx, with f : R −→ C.

This integral is not correctly d eﬁned without additional precision; indeed, if

f (x

) 6= 0, the function x 7→ f (x)/(x − x

) is not Lebesg ue integrable. One

possibility is to deﬁne the integral in the sense of the principal value.

We will assume that f is the restriction to the real axis of a function

meromorphic on C and holomorphic at x

. Moreover, we will assume that f

decays sufﬁciently fast at inﬁnity to permit t he use of the method of residues.

For insta nce, we will require that this decay holds at least in the upper half-

plane.

Now deﬁne a contour γ

as in Figure 8.1: denote by C

(ǫ) the small h alf-

circle with radius ǫ centered at x

and above the real axis. Letting the radius

of the large circle go to inﬁnity (and assuming the corresponding integral goes

to 0), we have then

f (z)

z − x

dz =

−ǫ

−∞

f (x)

x − x

dx +

+∞

f (x)

x − x

dx +

f (z)

z − x

dz ;

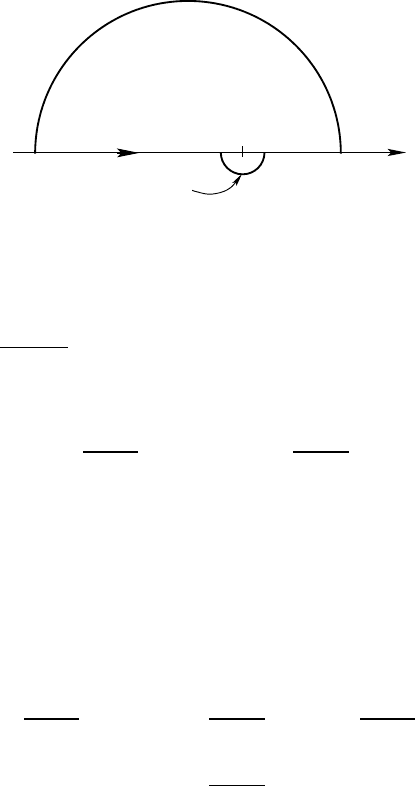
Cauchy principal value 225

−

(ǫ)

Fig. 8.2 — The contour γ

−

but the last integral is equal to

f (ǫ e

iθ

)

ǫ e

iθ

iǫ e

iθ

dθ = −iπ f (x

) + O(ǫ) [ǫ → 0

Thus, taking the limit [ǫ → 0

], we obtain

2iπ

p∈H

Res



f (z)

z − x

; p



= pv

+∞

−∞

f (x)

x − x

dx −iπ f (x

), (8.1)

where the sum

p∈H

is the sum over the poles of f located in the open

upper half-plane H

def

= {z ∈ C ; Im(z) > 0}.

So, to deal with the integral on a contour on which a pole is located,

it was necessary to deform this contour slightly — in this case, by making a

small detour around the pole to avoid it. One may wonder what would have

happened, had another detour been chos en. So take the contour γ

−

deﬁned

as in Figure 8.2. We then have

−

f (z)

z − x

dz = pv

+∞

−∞

f (x)

x − x

dx +

−

f (z)

z − x

= pv

+∞

−∞

f (x)

x − x

dx + iπ f (x

Since the integral on the left-hand side is equal to 2πi times the sum of the

residues located in t he upper half- plane, plus th e residue at x

, wh ich is equal

to 2πi f (x

), the ﬁnal formula is the sa me as (8.1).

8.1.c Feynman’s notation

When evaluating an integral on a contour that passes through a pole, it must

be speciﬁed on w hich side the pole the pole will be avoided (the result depends

only on the side that is chosen, not on the precise shape of the detour).

Rather than going around the pole, R ichard Feynman proposed modify-

ing the initial problem by moving the pole slightly off the real axis while

226 Distributions II

keeping the original contour intact. Suppose the function considered has a

pole on the real axis. Then one can write the symbolic equivalences

⇐⇒

and

⇐⇒

which means that the pole has been moved in the ﬁrst case to x

−iǫ and in

the second case to x

+ iǫ, and then the limit [ǫ → 0

] is taken at the end of

the computa tions.

To see clearly what this means, consider the equalities

f (z)

z − x

dz = lim

ǫ→0

f (z)

z − x

+ iǫ

dz = lim

ǫ→0

f (z)

z − x

+ iǫ

dz,

where γ is the undeformed contour. Indeed, the ﬁrst equality is a consequence

of continuity under the integral sign, and the second equality comes from

Cauchy’s theorem, which, for any given ǫ > 0, justiﬁes deforming γ

into γ,

since no pole obstructs this operation. Thus we get, performing implicitly the

operation “ lim

ǫ→0

,”

f (z)

z − x

dz =

+∞

−∞

f (x)

x − x

+ iǫ

dx = pv

+∞

−∞

f (x)

x − x

dx −iπ f (x

or, in a rather more compact fashion



x − x

+ iǫ

, f





x − x

, f



−iπ



δ(x − x

), f



Symbolically, we write:

x − x

+ iǫ

= pv



x − x



−iπ δ(x − x

and this formula must be applied to a meromorphic function f which is

holomorphic on the real axis.

Similarly, we have the following result:

x − x

−iǫ

= pv



x − x



+ iπ δ(x − x