Appel W. Mathematics for Physics and Physicists

Подождите немного. Документ загружается.

Solutions of exercises 177

Notice that it is of the stated perturbed form, with G(z) = V

/z.

One can show that, if |z| = a, th en Φ

′

(z) is tangent to the circle (i.e., Φ

′

(z) is orthogonal

to the circle).

The stagnation points of the ﬂuid are given by Φ

′

(z) = 0, which gives z = ±a.

 Solution of exercise 6 .6. Notice that the function which is proposed is the imaginary part

z 7−→ α L(z + 1) + β L(z −1) + γ,

where L is the holomorphic logarithm deﬁned on C wit h a cut along the lower half-plane. We

look for the constants α, β, and γ by noticing that on the boundary of the sheet, T = T

for

= θ

= π, T = T

for θ

= 0 and θ

= π, and T = T

for θ

= θ

= 0. We obtain then

T =

− T

+ T

− T

arctan



x + 1



− T

arctan



x − 1



+ T

❧

Chapter

Distributions I

7.1

Physical approach

7.1.a The problem of distribution of charge

We know that a point-like particle with electr ic charge q, placed at a point r

in the usual space R

, produces, at any point r in R

\{r

}, an electrostatic

ﬁeld

E( r) =

4πǫ

r − r

kr − r

. (∗)

If more charges are present, the linearity of the Maxwell equations ensures

that the ﬁelds created by all the charges is the sum of those created by each

charge. However, when working in macroscopic scale, it is sometimes better to

describe the distribution of charges in continuous form; it is then modeled by

a function ρ : R

→ R which associates, to ea ch point, the density of electric

charge at this point. The interpretation of the function ρ is the following:

if r

∈ R

and if d

r = dx dy dz is an elementary volume a round r

, then

ρ( r

) dx dy dz

represents the total charge contained in the elementary volume dx dy dz.

180 Distributions I

The electric ﬁeld at a point r is then (assuming the integral exists):

E( r) =

4πǫ

ZZZ

ρ( r

′

)

r − r

′

kr − r

′

, (∗∗)

and the tota l charge contained in a volume V ⊂ R

Q =

ZZZ

ρ( r) d

Can we reconcile the two expressions (∗) and (∗∗) for the point-like charge

and the density of ch arge respectively? In other words, can we write both

equations in a uniform way?

To express t he point-like charge with the “continuous” viewpoint, we

would need a function δ

describing a point-like unit charge located at r

This function would thus be zero on R

\ {r

}; moreover, when integrated

over a volume V , we would obta in

ZZZ

( r) d

r =

1 if r

∈ V ,

0 if r

/∈ V .

Generalizing, for any continuous function f : R

→ R, we would need to

have

ZZZ

f ( r) δ

( r) d

r = f ( r

). (7.1)

But, according to the theory of integration, since δ

is zero almost ev -

erywhere, the integral (7.1) is necessarily zero also. A “Dirac function” cannot

exist.

One may, following Dirac, use a sequence of functions with constant inte-

gral equal to 1, positive, and that “concentrate” around 0, as for instance:

(x) =

n if |x| ¶ 1/2n,

0 if |x| > 1/2n,

or its equivalent in three dimensions

( r) =

/4π if krk ¶ 1/2n,

0 if krk > 1/2n,

Every time the temptat ion ar ises to use the “δ-function,” the sequence of

functions (δ

)

n∈N

(resp. (D

)

n∈N

) can be used instead, and at the very end of

the computation one must take the limit [n → ∞]. Thus, δ

is replaced in (7.1)

by D

( r − r

), and the formula is written

ZZZ

f ( r) δ

( r) d

r = lim

n→∞

ZZZ

f ( r) D

( r − r

) d

r = f ( r

Physical approach 181

The reader can check that this formula is valid for any f unction f continuous

at r

(see for instance a fairly complete discussion of this point of view in the

book by Cohen-Tannoudji et al. [20, appendix II]). However, this procedure

is fairly heavy. This is what motivated Laurent Schwartz (and, independently,

on the other side of the Iron Curtain, Israël Gelfan d [38]) to create the

theory of distributions (resp. of generalized f unctions), which g ives a rig-

orous meaning to the “δ-function” and justiﬁes the preceding technique (see

Theorem 8.18 on page 232).

In the same manner we will want to des cribe not only the distribution of

point-like charges, but also a charge supported on a sur face or a curve, so that,

if we denote by ρ( r) the function g iv ing t he distribution of charges, we can

compute the total charge contained within the volume V with the formula

Q(V ) =

ZZZ

ρ( r) d

charges i in

the volume V

L ∩V

µ dℓ +

S ∩V

σ d

s +

ZZZ

vol.

( r) d

where ρ

vol.

is the volumic d ens ity of charge, σ the surface distribution on the

surface S , µ the linear distribut ion on the curve L , and q

the point-like

charges.

7.1.b The problem of momentum

and forces during an elastic shock

In this second exa mple, we will look at the problem of an elastic s hock b etween

two objects.

Consider a game of squash. Assuming that at a given time the ba ll reaches

a wall (orthogonally to the surface, to simplify) with velocity v

, and rebounds.

The b all gets “squashed” a little bit, so that the contact lasts for a period of

time ∆t which is nonzero; t hen it rebounds with velocity −v

. Hence the

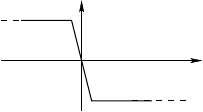
graph of t he speed of the ball as a function of time has the following shape:

Newton’s law stipulates t hat, during the movement, the force f exerted on

the ball is such that f = m˙v; it is therefore proportional to the derivative

of the function graphed above. Now if we wish to model in a simple way a

“hard” collision (where the “squashing” of the ba ll is not taken into account,

for instance, as in a game of “pétanque”), the graph of the speed becomes

182 Distributions I

and the force exerted should still be proportional to the derivative of this

function; in a word, f should be zero for any t 6= 0 and satisfy

+∞

−∞

f (t) dt = v(+∞) − v(−∞) = −2v

Once again, neith er the integral nor the previous derivative can be treated in

the usual sense of functions.

7.2

Deﬁnitions and examples of distributions

We will now present a mathematical tool “δ” which, a pplied to a contin-

uous function f , gives its value at 0, a relation which will be written

δ( f ) = f (0) or 〈δ, f 〉 = f (0).

The notation 〈δ, f 〉 is simply a convenient equivalent to δ( f ) so this means

that δ is a “machine that acts on functions,” associating them with a number.

Now the rule above happens to be linear as a function of f ; so it is natural

to apply it to elements of a certain vector space of functions (that may still be

subject to some choice). This object δ is th us what is called a complex linear

form or linear functional on a space of functions.

So we have

δ : space of functions −→ C,

function 7−→ number.

There remains to make precise on which space of functions the functional δ

(and other useful functionals) will be deﬁned.

DEFINITION 7.1 (Test function) Let n ¾ 1. The test space, denoted D(R

is the vector space of functions ϕ from R

into C, which are of class C

∞

and

have bounded support (i.e., they vanish outside some ball; in the case n = 1,

they vanish outside a bounded interval).

A test function is any function ϕ ∈ D(R

Bourbaki presents the operation of integration as a linear form on a space of f u nctions.

According to L. Schwartz, this abstract approach seems to have played a role in the genesis of

the theory of distributions.

Deﬁnitions and ex amples of distributions 183

When the value of n is clear or ir relevant in the context, we will simply

denote D instead of D(R

Example 7.2 There are an abundance of test functions, but it is not so easy to ﬁnd one. (In

partic u l ar because they are not analytic on R

— c an you see why?)

As an exercise, the reader will show that for a, b ∈ R with a < b, the function

ϕ(x) =







exp



(x −a)(x −b)



if x ∈ ]a, b[ ,

0 i f x ∈ ]−∞, a] ∪[b , +∞[

is a test function on R.

DEFINITION 7.3 A distribution on R

is any continuous linear f unctional

deﬁned on D(R

). T he distributions form a vector space called the topologi-

cal dual of D(R

), also called the space of distributions and denoted DD

′

(RR

)

or DD

′

For a distribution T ∈ D

′

and a test function ϕ ∈ D, the value of T at ϕ

will usually be denoted not T (ϕ) but instead 〈T , ϕ〉. Thus, for any T ∈ D

′

and any ϕ ∈ D, 〈T , ϕ〉 is a complex number.

Remark 7.4 This deﬁnition, simple in appearance, deserves some comments.

Why so many constraints in the deﬁnition of the functions of D? The reason is simple:

the topological dual of D gets “bigger,” or “richer,” if D is “small.” The restriction of the

space test D to a very restricted subset of functions produces a space of distribution which is

very large.

(This is therefore the opposite phe nomenon from wh at might have been e xpected from

the experience in ﬁnite dimensions.

)

The C

∞

regularity is necessary but the condition of bounded support can be relaxed, and

there is a space of functions larger than D which is still small e nough that most interesting

distributions belong to its dual. It is the Schwartz space S , which will be deﬁned on page 289.

A distribution T is, by deﬁnition, a continuous linear functional on D; thi s means that for

any sequence (ϕ

)

n∈N

of test functions that converges to a test function ϕ ∈ D, the sequence

of complex numbers (〈T ,ϕ

〉)

n∈N

must converge to the value 〈T , ϕ〉. To make this precise we

must ﬁrst specify precisely what is meant by “a sequence of test functions (ϕ

)

n∈N

converging

to ϕ.”

DEFINITION 7.5 (Convergence in DD

DD) A sequence of test functions (ϕ

)

n∈N

in D converges in DD

DD to a function ϕ ∈ D if

• the supports of the functions ϕ

are contained in a ﬁxed bounded

subset, independent of n;

For t hose still unconvinced: we may deﬁne a linear fu nct ional on D, w h ich to any test

function ϕ associates

ϕ(t) dt. However, if we had taken as D a space which is too large, for

instance, the space L

loc

of locally integrable functions (see Deﬁnition 7.8 on the next page), then

this functional would not be well-deﬁned since the integral

f (t) dt may have been divergent,

for instance, when f (t) ≡ 1. The functional ϕ 7→

ϕ(t) dt is thus well-deﬁned on the vector

space D of test functions, but not on the space of locally integrable functions. Hence it belongs

to D

′

but not to (L

loc

)

′

Recall that in ﬁnite dimensions the dual space is of the same dimension as the starting

space. Thus, the bigger the vector space, the bigger its dual.

184 Distributions I

• all the partial derivatives of all order of the ϕ

converge uniformly to

the corresponding partial derivative of ϕ: for n = 1, for inst ance, this

means

(p)

cv.u.

−−→ ϕ

(p)

for any p ∈ N.

Now the continuity of a linear functional T deﬁned on D ca n be deﬁned

in the following natural manner:

DEFINITION 7.6 (Continuity of a linear functional) A linear functional T :

D → C is continuous if and only if:











for any sequence (ϕ

)

n∈N

of test functions

in D,

if (ϕ

)

n∈N

converges in D to ϕ,

the sequence 〈T , ϕ

〉 converges in C to

〈T , ϕ〉.

Example 7.7 We can now show that the functional δ deﬁned by δ : ϕ 7→ ϕ(0) is continuous.

Let (ϕ

)

n∈N

be a sequence of test functions, converging to ϕ in D. Hence ϕ

cv.u.

−−→ ϕ, wh ich

implies the simple c o nvergence of (ϕ

)

to ϕ; in particular, ϕ

(0) tends to ϕ(0) in C. This

shows that 〈δ, ϕ

〉 tends to 〈δ, ϕ〉 in C, which e stablishes the continuity of δ.

7.2.a Regular distri butions

Distribut ions can be seen as a generalization of the notion of functions or,

more precisely, of locally integrable functions.

DEFINITION 7.8 A measurable function f : R

→ C is locally integrable if,

for any compact K ⊂ R

, the function f · χ

is integrable on K. The space

of locally integrable functions on R

is denoted L

loc

Functions which are locally integrable but not integrable are those which

have integrability problems at inﬁnity.

Example 7.9 The function x 7→ 1/

|x| is locally integrable (but not integrable on R, for it

decreases too slowly). More generally, any function in L

), L

), or L

) with p ¾ 1,

is locally integ rable.

Any locally integrable function deﬁnes then a distribution by means of

the following t heorem:

THEOREM 7.10 (Regular distributions) For any locally integra ble function f ,

there is an associated distribution, also denoted f , deﬁned by

∀ϕ ∈ D 〈f , ϕ〉

def

f (x) ϕ(x) dx.

Deﬁnitions and ex amples of distributions 185

Such a distribution is called the regular distribution associated to the locally inte-

grable function f .

Proof. It sufﬁces to show that the map ϕ 7→

f (x) ϕ(x) dx is indeed linear (whi ch

is obvious) and continuous.

Let (ϕ

)

n∈N

be a sequence of test functions converging to ϕ ∈ D. There exists a

bounded closed ball B such that B contains t h e supports of all the ϕ

. Since the

function f is locally integrable, we can deﬁne M =

|f | and this M is a ﬁnite real

number.

We then have



f (ϕ

−ϕ)



¶ M

|ϕ

−ϕ| ¶ M V kϕ

−ϕk

∞

, where V is the

ﬁnite volume of the ball B. But kϕ

−ϕk

∞

tends to 0 by the deﬁnition 7.5 and,

therefore, 〈f , ϕ

−ϕ〉 tends to 0. By linearity, 〈f , ϕ

〉 tends to 〈f , ϕ〉.

Remark 7.11 If the functions f and g are equal almost everywhere, the distributions f and g

will be equal, that is, 〈f , ϕ〉 = 〈g, ϕ〉 for any ϕ ∈ D. The converse is also true: if two regular

distributions are equal as functionals, then the corresponding functions are equal almost ev-

er ywhe re. The reader is invited to construct a proof of this fact using th e following property:

any integrable function with compact support can be approximated in the mean by functions

in D. So the notion of distribution is in fact an extension of the notion of classes of locally

integrable functions equal almost everywhere.

Example 7.12 Denote by 1 t he constant function 1 : x 7→ 1 (deﬁned on R). The regular

distribution associated to 1 is thus the map

1 : D −→ C,

ϕ 7−→ 〈1, ϕ〉 =

+∞

−∞

ϕ(x) dx.

Regular distributions will have considerable importance throughout this

chapter, since they are those which “look the most like” classical functions.

They will be used more than once to discover a new deﬁnition when time will

come to generalize to distributions certain concepts associated to functions

(such as the derivative, the Fourier transform, etc.).

7.2.b Singular distri butions

We now deﬁne the Dirac distribution:

DEFINITION 7.13 The Dirac distribution is th e distribution w hich, to any

function ϕ in D(R), associates its value at 0:

〈δ, ϕ〉

def

= ϕ(0) ∀ϕ ∈ D.

For a ∈ R, we deﬁne similarly the Dirac distribution centered at a, de-

noted δ

, by its action on any test function:

〈δ

, ϕ〉

def

= ϕ(a) ∀ϕ ∈ D.

Frequently (this will be justiﬁed page 189), δ

will instead be denoted δ(x −a).

The preceding deﬁnition is easily generalized to the case of many dimen-

sions:

186 Distributions I

The English physicist and mathematician Paul Adrien Maurice

Dirac (1902—1984) was one of the g reat founders of quantum

mechanics. One of his major achievements was to give, for the

ﬁrst time, a correct description of a quantum relativistic electron

(Dirac equation), interpreting the solutions with negative energy

that were embarrassing physici sts as antiparticles. He also showed

how the mathematical theory of groups could bring precious

information concerning parti cle physics. According to Dirac, the

mathematical beauty of a physical theory should be of paramount

importance.

DEFINITION 7.14 (Dirac Distribution on RR

) Let r

∈ R

be a point in R

The Dirac distribution at r

is the distribution deﬁned by its action on any

test f unction in D(R

, ϕ

def

= ϕ( r

) ∀ϕ ∈ D.

As b efore, it will often be denoted δ( r − r

Remark 7.15 We have thu s introduced a notation that may at ﬁrst lead to some

confusion: if T is a distribution, T ( r ) means not the value of T at the point r ,

which would make no sense,

but the distribution T itself; this serves as reminder that

the variable of the function on which T acts is denoted r .

DEFINITION 7.16 The Dirac comb is the distribution X

X (pronounced “sha”

)

deﬁned by its action on any test functions ϕ ∈ D(R):

〈X, ϕ〉

def

+∞

n=−∞

ϕ(n),

that is,

X =

+∞

n=−∞

or X(x)

def

+∞

n=−∞

δ(x −n).

Notice that the distribution X is well deﬁned, because the sum

ϕ(n)

is in fact ﬁnite (ϕ being, by deﬁnition, wit h bounded support).

The continuity is left as an (easy) exercise for th e reader.

The δ distribution is represented graphically by a vertical arrow, as here:

This bears repeating again at the risk of being boring: a distribution i s not a function, but

a linear form on a space of f u nctions.

This is a Cyrillic alphabet letter, corresponding to the sound “sh.”