Appel W. Mathematics for Physics and Physicists

Подождите немного. Документ загружается.

Chapter

Complex Analysis I

This chapter deals with the theory of complex-valued funct ions of one complex

variable. It introduces the notion of a holomorphic function, which is a function

f : Ω → C deﬁned and differentiable on an open subset of C. We will see that

the (weak) assumption of differentiability implies, in strong co ntrast with the real

case, t h e (much stronger) consequence that f is inﬁnitely differentiable. We wil l

then study functions with singularities at isolated points and which are holomorphic

except at th ese points; we will see that their study has important applications to

the computation of many integrals and sums, notably for the computation of the

Fourier transforms that occur in physics. In Chapter 5, we will see how techniques

of conform al analysis provide el egant solutions for certain p roblems of physics in

two dimensions, in particular, problems of electrostatics and o f incompressible ﬂuid

mechanics, but also i n the theory of diffusion and in particle physics (see also

Chapter 15).

4.1

Holomorphic functions

Whereas differentiability in R is a relatively weak constraint,

we will see

during the course of this chapter that differentiability in terms of a complex

variable implies by contrast many properties and “rigid iﬁes” the situation, in

a s ens e that will soon be made precise.

A function f , deﬁned on an open interval I of R and with values in R or C may be

differentiable at all points of I without, for instance, the derivative being continuous. For

instance, if we set f (0) = 0 and f (x) = x

sin(1/x) for all nonzero x, then f is differentiable

at all points of R, f

′

(0) = 0, but f

′

is not continuous at 0 (there is no limit of f

′

at 0 ).

88 Complex Analysis I

The life of Baron Augustin-Louis Cauchy (1789—1857) is quite

eventful since Cauchy, for political reasons (as a supporter of the

French monarchy), went into exile in Italy and then Prague. He

was a long-time teacher at the École Polytechnique. His work is

extremely wide-ranging, but it is to analysis that Cauchy brought

a fundamental contribution: a new emphasis on rigorous argu-

ments. He was one of th e ﬁrst to worry about proving the conver-

gence of various processes (in integral calculus and in the theory

of differential equations); he worked on determinants and intro-

duced the notation of matrices with double i ndices. In complex

analysis, his contributi ons are fundamental , as shown by the many

theorems bearing his name.

4.1.a Deﬁnitions

Let us start by deﬁning differentiability on the complex plane. Let Ω be an

open sub set of the complex

plane C, and let f : Ω → C be a complex-valued

function of a complex variable. Let z

∈ Ω be given.

DEFINITION 4.1 The f unction f : Ω → C is said to be differentiable at

∈ CC

CC if

′

)

def

= lim

z→z

f (z) − f (z

)

z − z

exists, i.e. , if there exists a complex number, denoted f

′

) such that



f (z) − f (z

) − f

′

) ×(z − z

)



= o(z − z

) [z → z

One may ask whether this deﬁnition is not simply equivalent to differen-

tiability in R

, after identifying the set of complex numbers and the real plane

(see sidebar 3 on page 134 for a reminder on basic facts about differentiable

functions on R

). The following th eorem, due to Cauchy, shows that this is

not the case and that C-differentiability is stronger.

THEOREM 4.2 (Cauchy-Riemann equations) Let f : Ω → C be a complex-

valued function of one complex variable; denote by

f the complex-valued function

on R

naturally associated to f , that is, the function

f : R

−→ C,

(x, y) 7−→

f (x, y)

def

= f (x + i y).

While we are speaking of this, we can recall that the study of the complex plane owes

much to the works of Rafaele Bombelli (1526—1573) (yes, so e arly!), who used i to solve algebraic

equations (he called it “di meno,” that is, “[root] of minus [one]”), and of Jean-Robert Argand

(1768—1822) who gave the interpretation of C as a geometric plane. The complex plane is

sometimes called “the Argand plane.” It is also Argand who introduced the mo dulus for a

complex number. The notat ion “i,” replacing the older notation

−1, is due to Euler (see

page 39).

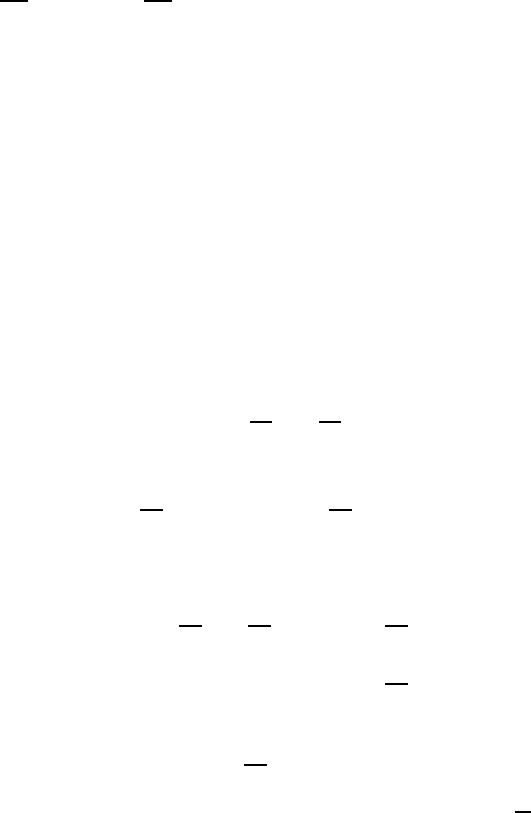
Holomorphic functions 89

Then the function f is C-differentiable at the point z

= x

+ i y

∈ Ω if and only if

f is R

-differentiable

∂

∂ x

, y

) = −i

∂

∂ y

, y







Cauchy-Riemann equation.

Proof

• Assume that f is differentiable in the complex sense at a point z

. We can deﬁne

a linear form d

f (z

) : R

→ C in the following manner:

f (z

)



(k, l)



def

= f

′

) ×



k + il



We have then, according to the deﬁnition of differentiability of f at z



f (x, y) −

f (x

, y

) −d

f (x

, y

)



(x − x

), ( y − y

)





= o(z − z

which shows that

f is R

-differentiable at the point (x

, y

). Moreover, since

f (x

, y

)(k, l) = f

′

)k + i f

′

)l,

it follows that

d f (z

) = f

′

) dx + i f

′

) dy.

Comparing with the formula

f =

∂

∂ x

dx +

∂

∂ y

(see page 134), we get

∂ f

∂ x

= f

′

) and

∂ f

∂ y

= i f

′

and therefore the required e quality.

• C o nversely: if

f is R

-differentiable and satisﬁes ∂

f /∂ x = −i∂

f /∂ y, then

f (x

, y

)



(k, l)





∂

∂ x

dx +

∂

∂ y

d y





(k, l)



∂

∂ x



dx + i dy



(k, l)



∂

∂ x

×(k + il),

which shows, by the deﬁnition of differentiability of

f , that



f (z) − f (z

) −

∂ f

∂ x

×(z − z

)



= o(z − z

and thus that f is differentiable and that its derivative is equal to f

′

) =

∂

∂ x

We henceforth write f instead of

f , except in special circumstances.

In the following, we will very of ten write a complex-valued function in th e

form

f = P + i Q with P = R e( f ), Q = Im( f ).

The relation obtained in the preceding th eorem allows us to write

90 Complex Analysis I

THEOREM 4.3 (Cauchy-Riemann equations) Let f : Ω → C be a function dif-

ferentiable at z

∈ Ω. Then we have the following equations:

∂ P

∂ x



, y

)

∂ Q

∂ y



, y

)

∂ Q

∂ x



, y

)

= −

∂ P

∂ y



, y

)











Cauchy-Riemann equations.

DEFINITION 4.4 Let Ω be an open subset of C. A function f : Ω → C is

holomorphic

at z

∈ CC

CC if it is differentiable at z

, and it is holomorphic

on Ω if it is holomorph ic at every point of Ω. We will denote by H (Ω) the

set of all functions holomorphic on Ω.

If A is a non-empty subset of C, a function f deﬁned on A is holomor-

phic on A if there exist an open neigh borhood Ω

′

of A and a holomorphic

function g on Ω

′

such that g(z) = f (z) for z ∈ A.

The following exercise (which is elementary) is an example of the “rigidit y”

of holomor phic functions that we mentioned before.

DEFINITION 4.5 A domain of C is a connected

open subset of C.

 Exercise 4.1 Show that if f : Ω → C is a f u nction holomorphic on a domain of C, the

following properties are equivalent:

(i) f is constant on Ω;

(ii) P = Re( f ) is constant on Ω;

(iii) Q = Im( f ) is constant on Ω;

(iv) |f | is constant on Ω;

(v) f is holomorphic on Ω.

(Solution on page 129)

4.1.b Examples

Example 4.6 The functions z 7→ z

, z 7→ e

, the polynomials in z, are holomorphic on C.

Example 4.7 The function z 7→ 1/z is holomorphic on C

∗

On the other hand, the function f : z 7→ ¯z is not differentiable a t any

point. I ndeed , let us show, for instance, that f is not differentiable at 0. For

The name holomorphic was introduced by Jean-Claude Bouquet (1819—1885) and his col-

league Charles Briot (1817—1882). Some texts use e quivalently the words “analytic” or “regular.”

A topological space is said to be connected if it is not the union of two disjoint open sets;

in other words, it is a set which is “in one pie ce”; see Appendix A.

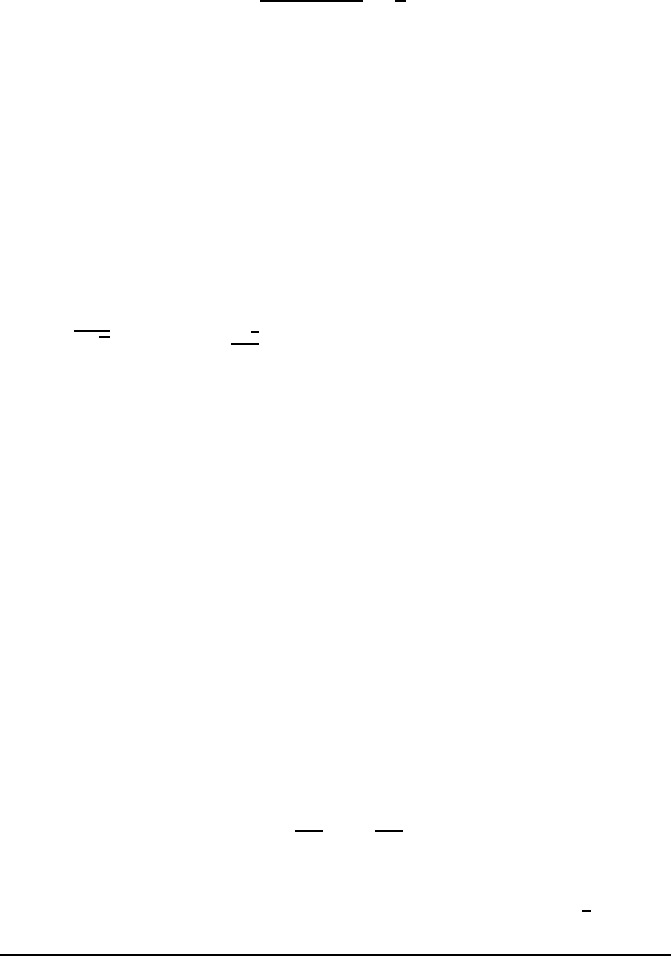
Holomorphic functions 91

this, we compute

f (z) − f (0)

z −0

¯z

If now we let z follow a path included in R approaching 0, this quotient is

equal to 1 thoughout the path, whereas if we let z follow a path included in

the set of purely imaginary numbers, we ﬁnd a constant value equal to −1;

this shows that the quantity of interest has no limit as z → 0, and thus that f is

not differentiable at 0. If we ad d a constant, we see that it is not differentiable

at z

for any z

Example 4.8 The function z 7→ |z| is nowhere holomorphic, and similarly for the functions

z 7→ Re(z) and z 7→ Im(z).

As a general rule, holomorphic functions will be those which depend “on

z only” (and of course sufﬁciently smooth), whereas those functions “that

depend not only on z but also on ¯z” will not be holomorphic, as for instance

|z| =

z · z or Re(z) =

z+z

. One may say that the variables z a nd ¯z are

treated as if the y were independent variables.

4.1.c The operators ∂/∂ z and ∂/∂ ¯z

We consider the plane R

, wh ich we will freely identify with C.

DEFINITION 4.9 We will denote by dx the linear form which associates its

ﬁrst coordinate to any vector (k, l) in R

. Similarly, we denote by dy the

linear form which associates its second coordinate to any vector (k, l) in R

dx(k, l) = k dy(k, l) = l.

We will write, moreover, dz

def

= dx + i dy and d¯z

def

= dx −i dy.

 Exercise 4.2 Show that the differential form dz = dx + idy is the identity (dz = Id

) and

that the differential form d¯z is the complex conjugation.

For any function f : Ω → C, R

-differentiable (and therefore not necessar-

ily differentiable in the complex sense), we have (check sidebar 3 on page 134):

d f =

∂ f

∂ x

dx +

∂ f

∂ y

dy.

The functions z = x + i y and ¯z = x − i y are R

-differentiable on R

≃ C;

moreover, dz = dx +i dy and d¯z = dx −i dy. We deduce that dx =

(dz +d¯z)

For those readers interested in theoretical physics, this treatment “as independent variables”

can be found also in ﬁeld theory, for instance in the case of Grassmann variables.

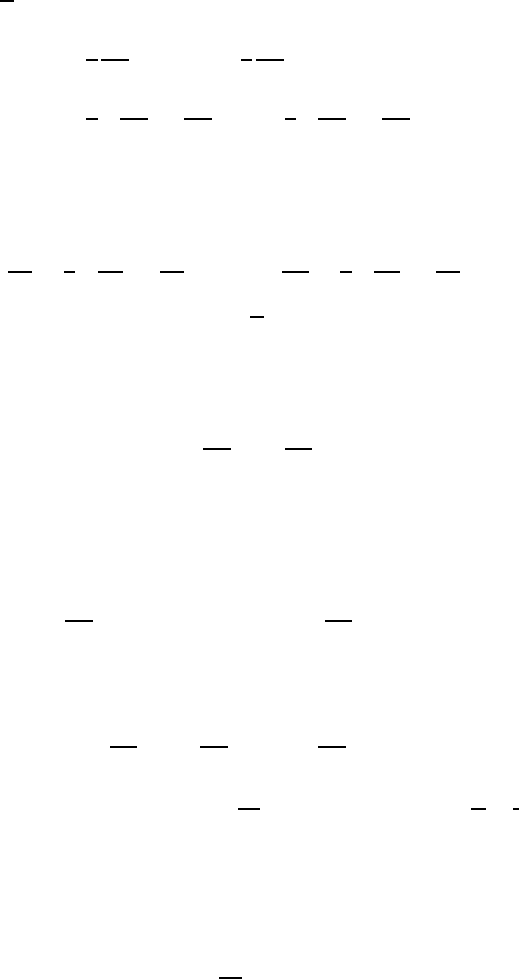
92 Complex Analysis I

and dy =

(dz −d¯z), which allows us to write:

d f =

∂ f

∂ x

(dz + d¯z) +

∂ f

∂ y

(d¯z −dz)



∂ f

∂ x

−i

∂ f

∂ y



dz +



∂ f

∂ x

+ i

∂ f

∂ y



d¯z.

This leads us to the following deﬁnition:

DEFINITION 4.10 We introduce the differential operators

∂

∂ z

def



∂

∂ x

−i

∂

∂ y



and

∂

∂ ¯z

def



∂

∂ x

+ i

∂

∂ y



We will sometimes denote them ∂ and ∂, when there is no ambiguity.

With these operators, the differential of a function R

-differentiable can there-

fore be written in the form

d f =

∂ f

∂ z

dz +

∂ f

∂¯z

d¯z.

We can then write another form of Theorem 4.2:

THEOREM 4.11 (Cauchy-Riemann equations) If f is C-differentiable, that is,

holomorphic, at z

, we have

∂ f

∂ z

) = f

′

) and

∂ f

∂¯z

) = 0.

This last relation is none other than the Cauchy-Riemann condition. One may write

also the two preceding equations as

∂ f

∂ z

) =

∂ f

∂ x

) = −i

∂ f

∂ y

Example 4.12 The function f : z 7→ Re(z) =

z+¯z

is not holomorphic because

∂ f

∂¯z

at e very

point.

Remark 4.13 We could also change our point of vie w and l oo k at functions that can be

expressed in terms of ¯z only:

DEFINITION 4.14 A function f : Ω → C is antiholomorphic if it satisﬁes

∂ f

∂ z

= 0

for all point in Ω.

Cauchy’s theorem 93

Remark 4.15 Be careful not to argue that “∂ f /∂ z = 0 at all points, so the fu nction

is constant,” which i s absurd. The function z 7→ ¯z does satisfy the condition, and

therefore is antiholomorph ic, but it is cert ainly not constant! The quantity ∂ f /∂ z is

equal to f

′

(z) only for a holomorphic function. For an arbitrary function, it does

not have such a clear meaning.

4.2

Cauchy’s theorem

In this section, we will describe various versions of a fundamental result of

complex analysis, which says that, under very general conditions, the integral

of a holomorphic function a round a closed path is equal to zero. We will start by

making precise what a path integral is, and then present a simple version of

Cauchy’s theorem (with proof), followed by a more general version (proof

omitted).

4.2.a Path integration

We now need a fe w deﬁnitions: argument, path, and winding number of a p ath

around a p oint.

DEFINITION 4.16 (Argument) Let Ω be an open subset of C

∗

= C \{0} and

let θ : Ω → R be a continuous function such tha t for z ∈ Ω we have

iθ(z)

|z|

Such a function θ is called a continuous determination of the argument. If

Ω is connected, then two continuous determinations of the argument differ

by a const ant integral multiple of 2π. There exists a unique continuous

determination of the argument

θ : C \R

−

−→ ]−π, π[

which satisﬁes θ(x) = 0 for any real number x > 0. It is called the principal

determination of the argument a nd is denoted “Arg.”

Remark 4.17 One should be aware that a continuous determination of th e arg u ment

does not necessarily exist for a given open subset. In particular, one cannot ﬁnd one

for the open subset C

∗

itself, since starting from argument 0 on the positive real axis

and making a complete circle around the origin, one comes back to this half-axis with

argument equal to 2π, so that continuity of the argument is not possible.

DEFINITION 4.18 (Curve, path) A curve in an open subset Ω in the complex

plane is a continuous map from [0, 1] into Ω (one may also allow other

94 Complex Analysis I

sets of deﬁnitions and take an arbitrary real segment [a, b] with a < b). If

γ : [0, 1] → Ω is a curve, we will denote by eγ its image in the plane; for

simplicity, we will also of ten write simply γ without risk of confusion. A

curve γ is closed if γ(0) = γ(1). It is simple if the image doesn’t “intersect

itself,” which means that γ(s) = γ(t) only if s = t or, in the case of a closed

curve, if s = 0, t = 1 (or the opposite). A path is a curve which is piecewise

continuously differentiable.

DEFINITION 4.19 (Equivalent paths) Two paths

γ : [a, b] → C and γ

∗

: [a

∗

, b

∗

] → C

are called equivalent if their images coincide and the corresponding curves

have the same orientation: γ([a, b]) = γ

∗

([a

∗

, b

∗

]), with γ(a) = γ

∗

γ(b) = γ

∗

(b). In other words, there exists a re-parameterization of the path

∗

, preserving the orientat ion, which transforms it into γ, which means a

bijection u : [a, b] → [a

∗

, b

∗

] which is continuous, piecewise differentiable

and strictly increasing, and such that γ(x) = γ

∗



u(x)



for all x ∈ [a, b].

Example 4.20 Let γ : [0, 2π] −→ C

t 7−→ e

i t

and γ

∗

: [0, π/2] −→ C

t 7−→ e

−2πi cos t

These deﬁne equivalent paths, with image equal to the unit circle.

If γ : [a, b] → Ω is a path, we have of course the formula

γ(b) −γ(a) =

′

(t) dt.

On the other hand, if f : Ω → R is a real-valued function, tw ice continuously

differentiable, then denoting by γ

and γ

the real and imaginary par ts of γ,

we have



γ(b)



− f



γ(a)





∂ f

∂ x



γ(t)



dγ

∂ f

∂ y



γ(t)



dγ



dt, (4.1)

the right-hand side of wh ich is nothing else, in two dimensions, than

∇f ·dℓ.

One must be aware that this formula holds only for a real-valued function.

DEFINITION 4.21 (Integral on a path) Let f : Ω → C be an arbitrary (mea-

surable) function (not necessarily holomorph ic), and γ a path with image

contained in Ω. The integral of f on the pat h γ is given, if the right-ha nd

side exists, by

f (z) dz

def



γ(t)



′

(t) dt. (4.2)

The path γ is called the integration contour.

Cauchy’s theorem 95

One checks (using the change of variable formula) that this deﬁnition

does not depend on the parameterization of the path γ, that is, if γ

∗

is a pat h

equivalent to γ, the right- hand integral is simultaneously deﬁned and gives

the same result with γ or γ

∗

. We then have th e following theorem:

THEOREM 4.22 Let f be a holomorphic function on Ω and γ : [a, b] → C a path

with image contained in Ω. Then



γ(b)



− f



γ(a)



∂ f

∂ z

(z) dz. (4.3)

Proof. We write f = f

+ i f

and then for each of the real-valued f u nctions f

and f

we app eal to formula (4.1). Formula (4.2), applied to ∂ f /∂ z, and the Cauchy

conditions then imply the result.

Remark 4.23 This formula is only valid if f is a holomorphic function. If we take the

example of the function f : z 7→ ¯z, which is not holo mlorphic, we have ∂ f /∂ z = 0

at all points of C. Formula (4.3) does not apply, since otherwise it would follow that

f is identically zero! An extension of th e formula, valid for any complex function

(holomorphic or not) is given in Theorem 4.51 on page 106 (the Green formula).

DEFINITION 4.24 The length of a path γ is the quantity

def



′

(t)



dt.

We t hen have the following intuitive property: the integral of a function

along a path is at most t he length of the path multiplied by the supremum

of the modulus of the function.

PROPOSITION 4.25 If f is holomorphic on Ω and if γ is a path contained in Ω,

then



f (z) dz





sup

z∈γ



f (z)





×L

4.2.b Integrals along a circle

Some integrals can be computed easily using a suitable parameteriz ation of

the path; this is the case for instance for integrals along circles.

Consider the circle C (a ; R) centered at the point a with radius R, with pos-

itive (counterclockwise) orientation; one can use t he parameteriza tion given by

γ : [0, 2π] −→ C,

θ 7−→ a + R e

iθ

and, therefore, we have z = a + R e

iθ

and dz = iR e

iθ

96 Complex Analysis I

PROPOSITION 4.26 (Integral along a circle) Let a ∈ C and R > 0. Let f be a

function deﬁned on an open subset Ω in C containing the circle γ = C (a ; R). Then

f (z) dz =

2π

f ( a + Re

iθ

) iR e

iθ

dθ.

As an example, let us compute t he integral of the function z 7→ 1/z on

the unit circle. The path can be represented by γ : [0, 2π] → C, θ 7→ z = e

iθ

We ﬁnd

2π

iθ

dθ = 2iπ. (4.4)

4.2.c Winding number

THEOREM 4.27 (and deﬁnition) Let γ be a closed path in C, U the complement

of the image of γ in the complex plane. The winding number of γ around the

point z is given by

Ind

(z)

def

2πi

dζ

ζ − z

for all z ∈ U . (4.5)

Then Ind

(z) is an integer, which is constant as a function of z on each connected

component of U and is equal to zero on the unbounded connected component of U .

Proof. See Appendix D.

Example 4.28 A small picture is more eloquent than a long speech.

The picture on the ri ght shows the various values of the function Ind

for

a c u rve in the complex p l ane. One sees th at the meaning of the value of the

function Ind

is ver y simple: for any point not on γ, it gives the number

of times the curve turns around z, t his number being counted algebraically

(taking orientation into account). Being in the unbounded c o nnected com-

ponent of U means simply being entirely outside the loop.

 Exercise 4.3 Show by a direct computation that if γ is a circle with center a and radius r,

positively oriented, then

Ind

(z) =

1 if |z −a| < r,

0 if |z −a| > r.

4.2.d Various forms of Cauchy’s theorem

We a re now going to show that if f ∈ H (Ω), where Ω is open and “has no

holes,” and if γ is a path in Ω, then the integral of f along γ is zero.

We start with the following simple result:

PROPOSITION 4.29 Let Ω be an open set and γ a closed path in Ω. If F ∈

H (Ω) and F

′

is continuous, then

′

(z) dz = 0.