Appel W. Mathematics for Physics and Physicists

Подождите немного. Документ загружается.

The integral according to Mr. Lebesgue 57

Fig. 2.4 — S

n−1

( f ) (dark gray) is less than S

( f ) (light gray).

2.2.b Borel subsets

We now take up the question of measuring the “size” of a subset A of R. As

we will see, it turns out to be impossible to assign a measure to all subsets

of R. It is necessary to restrict which subsets are considered; they are called

“measurable sets.” Since it is nat ural to expect t hat the union A ∪ B of two

subsets which can be measured should also be measurable, and since analysis

quickly requires some inﬁnite unions, t he following deﬁnition is reasonable:

DEFINITION 2.5 Let X be an arbitrary set. The set of subsets of X is denoted

P(X ). A σ-algebra

on X is any subset T ⊂ P(X ) of the set of subsets of X

such that the following conditions hold:

(T1) X ∈ T and ∅ ∈ T ;

(T2) for all A ∈ T , the complement X \ A is also in T ;

(T3) if (A

)

n∈N

is a sequence of elements of T , then

∞

n=0

∈ T .

Hence a σ-algebra T is stable by complement and countable union. More-

over, since the complement of the union of a family of sets is the intersection

of their complements, T is also stable by count able intersections.

Example 2.6 P(X ) is a σ-algebra (the largest σ-algebra on X ); {∅, X } is also a σ-algebra (the

smallest). For a ∈ X ,



∅, X ,{a}, X \{a}



is a σ-algebra.

Consider a subset X of P(X ) (hence a set, the elements of which are

themselves subs ets of X ). The intersection of all σ-algebras containing X is

still a σ-algebra, and of course it is contained in any σ-algebra containing X .

An algebra is a set of subsets stable under complement and ﬁnite u nion. The “σ” preﬁx

indicates the countable operations which are permitted.

58 Measur e t heo ry and the Lebesgue integral

Émile Borel (1871—1956), was ranked ﬁrst at the entrance exami-

nation of both the É cole Polytechnique and the École Normale

Supérieure. He chose the latter school and devoted himself to

mathematics; to Marguerite, daughter of Paul Ap pell (also a fa-

mous writer under the pseudonym Camille Marbo); and to pol-

itics (in the footsteps of Painlevé). In 1941, he was jailed in

Fresnes because of his opposition to the regime of Vichy, and be-

came a member of the resistance as soon as he was freed. In 1956,

he received the ﬁrst Gold Medal from the CNRS. He founded

the I nstitut Henri-Poincaré. Among his most important works,

we c an mention that he studied the measurability of sets, and in

partic u l ar deﬁned the se ts of reals of measure zero and the Borel

sets, on which Lebesgue measure is well deﬁned. He also worked

in probability theory and mathematical physics (the kinetic the-

ory of gas). His student Henri Lebesgue (see page 61) used h is

results to develop his theory of integration.

This is th erefore t he smallest σ-algebra containing X . This leads to the

following deﬁnition:

DEFINITION 2.7 Let X ⊂ P(X ). The σ-algebra generated by X is the

smallest σ-algebra containing X . It is denoted TT

TT (XX

XX ). For A ⊂ X , the

σ-algebra generated by A is the σ-algebra T (A) generated by X = {A}.

Example 2.8 For a ∈ X , the σ-algebra generated by {a} is



∅, X ,{a}, X \ {a}



DEFINITION 2.9 (Borel sets) The Borel σ-algebra is the σ-algebra on R gen-

erated by the open subsets of R. It is denoted B(R). Its elements are called

Borel sets.

It is easy to check th at the Borel σ-algebra is also the σ-algebra generated

by intervals of R of the type ]−∞, a], where a ranges over all real numbers.

In particular, the following sets are Borel subsets of R:

1. all open sets;

2. all closed sets (since their complement is open);

3. all countable unions and intersections of open and closed sets.

However, there are many others! The Borel σ-algebra is much more complex

and resists any simple-minded exhaustive description.

This is of great importance in probability theory, wh ere it is used to reduce the study of a

random variable to the study of its distribution function.

The integral according to Mr. Lebesgue 59

2.2.c Lebesgue measure

It is unfortunately beyond t he s cope of th is book to describe the construction

of the Leb esgue measure in all details. Interested readers are invited to look ,

for instance, in Rudin’s b ook [76] or in Burk’s very clear course [16].

DEFINITION 2.10 A measurable space is a pair (X , T ), where X is an arbi-

trary set and T is a σ-algebra on X . Elements of T are ca lled mea surable

sets.

DEFINITION 2.11 Let (X , T ) be a measurable space. A measure on (X, TT

TT ),

or on X, by abuse of notat ion, is a map µ deﬁned on th e σ-algebra T , with

values in R

def

= R

∪{+∞}, such that

(MES1) µ(∅) = 0;

(MES2) for any countable family (A

)

n∈N

of pairwise disjoint measurable

sets in T , we have



∞

[

n=0



∞

i=0

µ(A

The second property is called the σ-additiv ity of the measure.

A measure space

is a triple (X , T , µ), where (X , T ) is a measurable space

and µ is a measure on (X , T ).

Remark 2.12 Since a measure takes values in R

def

= R

∪{+∞}, it is necessary to specify the

addition rule involving +∞, namely,

x + ∞ = +∞ for all x ∈ R

Note that the usual property “(x + z = y + z) =⇒ (x = y)” is no longer valid in full generality

(e.g., 2 + ∞ = 3 + ∞); however, it holds if z 6= +∞.

The following theorem, due to Lebesgue, shows that there exists a measure

on the Borel σ-algebra which extends the length of an inter val.

THEOREM 2.13 (The Lebesgue measure on Borel sets) The pair (R, B) is a

measurable set and there exists on (R, B) a unique measure µ such that



[a, b]



= |b − a| for all a, b ∈ R.

The idea for the construction of the Lebesgue measure is described in

Sidebar 1 on th e following page.

The Lebesgue measure µ is translation-invariant (i.e., translating a measur-

able set does not change its measure), and is diffuse (th at is, for any ﬁnite or

Note that very similar deﬁnitions will app ear in Chapter 19, concerning probability spaces.

60 Measure theory an d the Lebesgue integral

Sidebar 1 (Lebesgue measure for Borel sets)

Consider the “length” ma p ℓ which associates its length b − a to any ﬁnite

interval [a, b]. We tr y to extend this deﬁnition to an arbitrary subset of R.

Let A ∈ P(R) be a n arbitrary subset of R.

Let E (A) be the set of all sequences A = (A

)

n∈N

of intervals such that A is

contained in

∞

i=0

. For any A = (A

)

n∈N

∈ E (A), let

λ(A )

def

∞

i=0

ℓ(A

and deﬁne the Lebesgue exterior measure of A as follows:

∗

(A)

def

= inf

A ∈E (A)

λ(A ).

Unfortunately, this “exterior measure” is not a measure as deﬁned previously: the

property of σ-additivity (MES2) is not satisﬁed (this would contradict the result of

Sidebar 2).

On the other ha nd, one can show that the restriction of λ

∗

to the Borel σ-algebra

µ : B −→ R

A 7−→ µ(A) = λ

∗

(A)

is a measure (this is by no means obvious or easy to prove). It is the Lebesgue

measure for Borel sets.

countable set ∆, we have µ(∆) = 0). In particular, µ(N) = µ(Z) = µ(Q) = 0.

Note that the converse is false: for instance, the C antor triadic set is not count-

able, yet it is of measure zero (s ee Exercise 2.5 on page 68).

2.2.d The Lebesgue σ-algebra

The Lebesgue measure on Borel sets is sufﬁcient for many applications (in

particular, it is commonly used in probability theory).

Never theless , it is interesting to know that the construction may be reﬁned.

Consider a Borel set A wit h measure zero. There may exist subsets B ⊂ A

which are not of meas ure zero, simply because B is not a Borel set, and hence

is not meas urable. But it seems intuitively obvious that a subset of a set of

measure zero should also be considered negligible and be of meas ure zero (in

particular, measurable). In fact, it is possible to deﬁne a σ-algebra containing

all Borel sets, and all subsets of Borel sets with Lebesgue measure zero, and

to extend the L ebesgue measure to this σ-algebra. This σ- algebra is called the

Lebesgue σ-algebra and is denoted L . We have therefore B ⊂ L . (The

construction of L and of the required extension of the Lebesgue measure are

again beyond the scope of t his book.) We thus have:

The integral according to Mr. Lebesgue 61

Henri Lebesgue (1875—1941), son of a typographical worker,

entered the École Normale Supérieure, where he followed the

courses of Émile Borel. In 1901, he p u blished in his thesis the

theory of the Lebesgue measure, generalizing previous work of

Borel (and also of Camille Jordan and Giuseppe Peano). The

following year, he developed his theory of integration, and used

it to study series of functions and Fourier series. He proved that

a bounded function is integrable in the sense of Riemann if and

only if it is continuous except on a negligible set. In h is l ater

years, Lebesgue turned against analysis and would only discuss

elementary geometry.

PROPOSITION 2.14 Let A be an element of the Lebesgue σ-algebra such that

µ(A) = 0. Then any subset B ⊂ A is in the Lebesgue σ-algebra and sa tisﬁes

µ(B) = 0.

This property is called completeness of the measure space (R, L , µ) or of

the Lebesg ue σ-algebra.

The Borel σ-algebra is not complete, which justiﬁes

the introduction of the larger Lebesgue σ-algebra.

Remark 2.15 In the remainder of this and the next chapter, we will consider the Lebesgue measure

on the Lebesgue σ-algebra, and a measurable set will be an element of L . Note that in practice

(for a physicist) th ere is really no difference between the Lebesgue and Borel σ-algebras.

2.2.e Negligible s ets

DEFINITION 2.16 A subset N ⊂ X of a measure space (X , T , µ) is negligi-

ble if it is contained in a measurable set N

′

∈ T such t hat µ(N

′

) = 0.

In particular, a subset N of R is negligible if and only if it is in th e

Lebesgue σ-algebra and is of Lebesgue measure zero.

Remark 2.17 In terms of the simpler Borel σ-algebra, a subset N of R is negligible if and only

if there exists a Borel set N

′

containing N which is of Lebesgue measure zero. But N itself is

not necessarily a Borel set.

Example 2.18 The set Q of rational numbers is negligible since, using σ-additivity, we have

µ(Q) =

r∈Q



{r}



r∈Q

0 = 0.

DEFINITION 2.19 A property P deﬁned for elements of a measure space

(X , T , µ) is true for almost all x ∈ X or holds a lmost everywhere, ab-

breviated holds a.e., if it is true for all x ∈ X except those in a negligible

set.

This is not the same notion as completeness of a topological space.

62 Measure theory and the Lebesgue integral

Example 2.20 The Heaviside function

H : x 7−→

0 if x < 0 ,

1 if x ¾ 0 ,

is differentiable almost everywhere.

The Dirichlet function

D : x 7−→

1 if x ∈ Q,

0 if x ∈ R \Q,

is zero almost everywhere.

DEFINITION 2.21 Let (X , T ) and (Y , T

′

) be measurable spaces. A function

f : X → Y is measurable if, for any measurable subset B ⊂ Y , the set

−1

(B)

def



x ∈ X ; f (x) ∈ B



of X is measurable, that is, if f

−1

(B) ∈ T for all B ∈ T

′

This deﬁnition should b e compared with the deﬁnition of continuity of a

function on a topological space (see Deﬁnition A.3 on page 574).

Remark 2.22 In practice, all funct ions deﬁned on R or R

that a physicist (or almost any

mathematician) has to deal with are measurable, and it is usually pointless to bother checking

this. Why is that the case? The reason is that it is difﬁcult to exhibit a nonmeasurable function

(or even a single nonmeasurable set); it is necessary to invoke at some point the Axiom of Choice

(see Sidebar 2), whic h is not physically likely to happen. The famous Banach-Tarski paradox

shows that nonmeasurable sets may have very weird properties.

2.2.f Lebesgue measure on RR

Part of the power of measure theory as deﬁned by Lebesgue is that it extends

fairly easily to product spaces, and in particular to R

. First, one can consider

on R ×R the σ-algebra generated by sets of the type A × B, where (A, B) ∈

B(R)

. This σ-algebra is denoted B(R) ⊗ B(R); in fact, it can be shown

to coincide with the Borel σ-algebra

of R

with the usual topology. It is

Consider a solid ball B of radius 1 in R

. There exists a way of partitioning th e ball in

ﬁve disjoint pieces B = B

∪ ··· ∪ B

such that, after translating and rotating the pieces B

suitably — without dilation of any kind — the ﬁrst two and the last three make up two distinct

balls of the same radius, not missi ng a single point:

7−→

It seems that this result ﬂies in the face of the principle of “conservation of volume” during a

translation or a rotation. But that is the point: the pieces B

(or at least some of them) are not

measurable, and so the notion of “volume” of B

makes no sense; see [74].

In the sense o f the σ-algebra generated by open sets.

The integral according to Mr. Lebesgue 63

then possible to prove that there exists a unique measure denoted π = µ ⊗µ

on B(R) ⊗B(R) which is given on recta ngles by the natural deﬁnition

π(A × B) = µ(A) µ(B)

for A, B ∈ B(R). This measure is called the product measure, or the

Lebesgue measure on R

. The construction may be repeated, yielding a Borel

σ-algebra and a Lebesgue measure on R

for all n ¾ 1.

2.2.g Deﬁnition of the Lebe sgue inte gral

Here we give a general deﬁnition of the Lebesgue integral on an arbitrary

measure space (X , T , µ), which — in a ﬁrst reading — the reader may assume

is R with the Lebesgue measure. It yields the same results as the construction

sketched in Section 2.2.a, but the added generality is convenient to prove the

important results of the Lebesgue integ ral calculus.

The ﬁrst step is to deﬁne the integral for a non-negative measurable simple

function (i.e., a function taking only ﬁnitely many values). This deﬁnition

is then extended to non-negative functions, a nd ﬁnally to (some) real- or

complex-valued measurable functions.

DEFINITION 2.23 (Simple function) Let X be an arbitrary set, A ⊂ X a sub-

set of X . The characteristic function of A is the function χ

: X → {0, 1}

such that χ

(x) = 1 if x ∈ A a nd χ

(x) = 0 ot herwise.

Let (X , T ) be a measurable space. A function f : X → R is a s imple

function if there exist ﬁnitely many disjoint measurable sets A

, . . . , A

in T

and elements α

, . . . , α

in R such that

f =

i=1

Now if (X , T , µ) is a meas ure space and f is a non-negative simple function

on X , the integral of f with respect to the measure µ is deﬁned by

f dµ

def

i=1

µ(A

which is either a non-negative real number or +∞. I n this deﬁnition, the

convention ∞×0 = 0 is used if either α

= ∞ or µ(A

) = ∞. If the integral

of f is ﬁnite, then f is integrable.

Remark 2.24 In the case where X = R and µ is the Lebesgue measure, the following notation

is also used for the integral of f with respect to µ:

f dµ =

f (x) dx =

+∞

−∞

f (x) dx.

64 Measure theory and the Lebesgue integral

Example 2.25 Let D be the Dirichlet function, which is 1 for rational numbers and 0 for

irrational numbers. Then D is a simple function (since Q is measurable), and

[0,1]

(1 − D) dµ = 1 whereas

(1 − D) dµ = +∞.

The deﬁnition is extended now to any measurable non-negative function.

DEFINITION 2.26 (Integral of a non-negative function) Let (X , T , µ) be a

measure space and let f : X → R

be a measurable function with non-

negative values. The integral of f is deﬁned by

f dµ

def

= sup

Z

g dµ ; g simple such that 0 ¶ g ¶ f



It is eith er a non-negative real number or +∞. If it is ﬁnite, then f is

integrable.

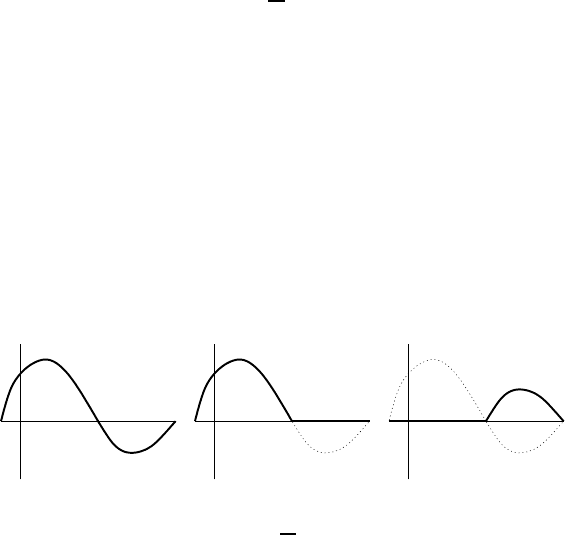
Finally, to deal with real-valued measurable functions f , the decomposition

of f into its non-negative and non-positive parts is used: The non-negative

part of a function f on X is the function f

def

= max( f , 0), and the non-

positive part of f is the function f

−

def

= max(−f , 0). We have f = f

− f

−

and the functions f

and f

−

are non-negative measurable functions.

f f

−

DEFINITION 2.27 (Integrability and integra l of a function) Let (X , T , µ) be

a measure space and let f : X 7→ R be a measurable function, E ⊂ X a

measurable set. Then f is integrable on E with respect to µ or f is µ-

integrable, if

dµ and

−

dµ are both ﬁnite, or equivalently if the

non-negative function |f | is integrable on E. The integral of f on E with

respect to µ is then

f dµ

def

dµ −

−

dµ.

If f is a measurable complex-valued function, one looks separately at the real

and imaginary parts Re( f ) and Im( f ). If both are integrable on X with

respect to µ, then so is f and we have

f dµ =

Re( f ) dµ + i

Im( f ) dµ.

The integral according to Mr. Lebesgue 65

In practice, the deﬁnitions above are justiﬁed by the fact that any mea-

surable function f is the pointwise limit of a sequence ( f

)

n∈N

of simple

functions. If, moreover, f is bounded, it is a uniform limit of simple func-

tions.

As it should, the Lebesgue integ ral enjoys the s ame formal properties as

the Riemann integral. I n par ticular, the following properties hold:

PROPOSITION 2.28 Let (X , T , µ) be a measure space, and let f , g be measurable

functions on X , with values in R or C. Then we have:

i) if f and g are integra ble with respect to µ, then for any complex numbers α,

β ∈ C, the function α f + βg is integrable and

(α f + βg) dµ = α

f dµ + β

g dµ;

ii) if f and g are integrable and real-valued, and if f ¶ g, then

f dµ ¶

g dµ;

iii) if f is integrable, then



f dµ



|f | dµ;

iv) if g is non-negative and integrable and if |f | ¶ g, then f is integrable and

|f | dµ ¶

g dµ.

Finally, under some suitable assumptions,

for any two meas ure spaces

(X , T , µ) and (Y , T

′

, ν), the product measure space (X ×Y , T ⊗T

′

, µ ⊗ν)

is deﬁned in such a way that Fubini’s formula holds: for any integrab le

function f on X × Y , we h ave

X ×Y

f d(µ ⊗ν) =

Z

f (x, y) dν( y)



dµ(x)

Z

f (x, y) dµ(x)



dν( y)

(an implicit fact here is that the integral with respect to one variable is a

measurable function of the ot her variable, so that all integrals which appear

make sense). In other words, the integral may be computed in any order (ﬁrst

over X then Y and conversely). Moreover, a meas urable function f deﬁ ned

on X × Y is integrab le if either



f (x, y) dν( y)



dµ(x) or



f (x, y) dµ(x)



dν( y)

This should be compared with the Riemann deﬁnition of integral, where step functions

are used. It t u rns out that th ere are relatively few functi ons which are uniform limits of step

functions (because step funct ions, constant on intervals, are much more “rigid” than simple

functions can be, deﬁned as they are using arbitrary measurable sets).

Always satisﬁed in applications.

66 Measure theory and the Lebesgue integral

is ﬁnite.

All this applies in particular to integrals on R

with respect to the Lebesgue

measure µ ⊗ µ, and by induction on R

for d ¾ 1. The Fubini formula

becomes

f (x, y) dx dy =

Z

f (x, y) dy



Z

f (x, y) dx



dy.

The following notat ion is also commonly used for integrals on R

f d

µ =

f d(µ ⊗µ) =

f (x, y) dx dy

f (x, y) dµ(x) dµ( y).

2.2.h Functions zero almost everywhere,

space L

of integrable functions

PROPOSITION 2.29 Let (X , T , µ) be a measure space, for instance, X = R with

the Lebesgue σ-algebra and measure. Let f : X → R

∪{+∞} be a non-negative

measurable f unction. Then we have

f dµ = 0 ⇐⇒ f is zero almost everyw here.

Proof. See Exercise 2.7 on page 69.

In particular, if the values of an integrable function f are changed on a

set of measure zero, the integral of f does not change. We have

f = g a.e. =⇒

f dµ =

g dµ.

In the cha pter concerning d istributions, we will see that two functions

which differ only on a set of measure zero should not be considered to be

really different. Hence it is common to say that such functions are equal,

instead of merely

“equal almost everywhere.”

DEFINITION 2.30 (L

spaces) Let (X , T , µ) be a measure space. The space

(X, µ) or simply L

(X) if no confusion concerning µ can arise, is the

This is not simply an abuse of notation. Mathematically, what i s done is take the se t of

integrable functions, and take its quotient modulo th e equivalence relation “being equal almost

everywhere.” This means that an element in L

(X ) is in fact an equivalence class of functions.

This notion will come back during the course.