Appel W. Mathematics for Physics and Physicists

Подождите немного. Документ загружается.

Solutions of exercises 47

iii) Show that the function x 7−→

1 + x

is 1-Lipschitz on R, i.e.,



1 + y

−

1 + x



¶ |y − x|. (1.8)

iv) Show that Φ is a contracting map if a is sufﬁciently small.

v) Show that there exists a u nique solution to the Cauchy problem. Give an explicit

iterative method to solve the system numerically (Picard iterations).

Remark 1.79 In general, all this detailed work need not be done: the Cauchy-Lipschitz theorem

states that for any continous function ψ(x, y) which is locally Lipschitz w ith respect to the

second variable, the Cauchy problem

′

= ψ(t, y),

has a unique maximal solution (i.e., a solution deﬁned on a maximal interval).

SOLUTIONS

 Solution of exercise 1.2. The energy of the circuit at the beginning of th e experiment is

the energy contained in the charged capacitor, namely E = Q

/2C . At equilibrium, when

[t → ∞], no current ﬂows, and the charge of each capacitor is Q /2 (it is possible to write

down the necessary differential equations and solve them to check this). Thus the ﬁnal energy

is E

′

= 2(Q/2)

/C = E/2. The energy which is dissipated by the Joule effect (computed by

the integral

+∞

(t) dt, whe re t 7→ i(t) is the current ﬂowing through the circuit at time t)

is of course e qual to E − E

′

, and does not depend on R.

However, if R = 0, one observes oscill ations of charge in each c apacitor. The total energy

of the system is conserved (it is not possible to compute it from relations in a quasi-stationary

regime; one must take magnetic ﬁelds into account!). In particular, as [t → +∞], the initial

energy is recovered. The explanation for this apparent contradiction is similar to what hap-

pened for Romeo and Juliet: the time to reach equilibrium is of order 2/RC and tends to

inﬁnity as [R → 0]. This is a t ypical situation where the limits [R → 0] and [t → +∞] do

not commute.

Finally, if we c arry the computations even farther, it is possible to take into account the

electromagnetic radiation due to the variati o ns of the elect ric and magnetic ﬁelds. There is

again some loss of energy, and for [t → +∞], the ﬁnal energy E − E

′

= E/2 is recovered.

 Solution of exercise 1.3. Light sources are never purely monochromatic; otherwise there

would indeed be no spatial coherence problem. What happens is that light is emitted in wave

packets, and the spectrum of the source necessarily has a certain width ∆λ > 0 (in a typical

example, t his is order of magnitude ∆ν = 10

−1

, corresponding to a coherence length o f a

few microns for a standard light-bulb; the coherence length of a small He-Ne laser is around

thirty centi meters, and that of a monomode laser can be several miles). All computations must

be done ﬁrst with ∆λ 6= 0 before taking a limit ∆λ → 0. Thus, surprising ly, spatial coherence

is also a matter of temporal coherence. This is often hidden, with the motto being “si nce the

sources are not coherent, I must work by summing intensities instead of amplitudes.”

In fact, when considering an interference ﬁgure, one must always sum amplitudes, and t hen

(this may be a memory from your optics course, or an occasion to read Born and Wolf [14])

perform a time average over a period ∆t, which may be very small, but not too much (depending

on the receptor; the eyes are pretty bad in this respect, an electronic receptor is better, but none

can have ∆t = 0).

48 Reminders concerning convergence

The delicate issue is to be careful of a product ∆t ·∆λ. If you come to beli eve (wrongly!)

that two purely monochromatic sources interfere withou t any spatial coherence defect, this

means that you have assumed ∆t · ∆λ = 0. To see the spat ial coherence issue arise, one must

keep ∆λ large enough so that ∆t ·∆λ cannot be neg lected in the computation.

 Solution of exercise 1.7. Let P

k=1

/k. It is easy to see th at (P

)

n∈N

is a Cauchy

sequence: for any integers k and p, we have



p+k

− P



p+1

However, t his se quence does not converge in K[X ]; indeed, if it were to converge to a

limit L, we would have L ∈ K[X ], and all coefﬁcients of L of degree large enough (¾ N,

say) would be zero, which implies that kP

− Lk ¾ 1/(deg L + 1) if k ¾ N , contradicting that

)

n∈N

converges to L.

This example shows that K[X ] is not complete.

 Solution of exercise 1.9. For any n ∈ N, we have

= n/2 , and for any x ∈ [0, 1], the

sequence



(x)



tends to 0, showing that

lim

n→∞

(x) dx = +∞ whereas



lim

n→∞

(x)



dx = 0 .

 Solution of exercise 1.11. The se quence (ϕ

)

n∈N

converges uniformly to 0.

Notice also the property

(0) = 0, ϕ

′

(0) = 1, ϕ

(k)

(0) = 0 ∀k ¾ 2.

For gi ven ǫ > 0, it sufﬁces to deﬁne Ψ

as t he (p − 1)-st primitive of ϕ

, where N is

sufﬁciently large so that sup

x∈[−1,1]



(p−1)

(x)



¶ ǫ. Here, each primitive is selected to be the

one vanishing at 0 (i.e., the integral from 0 to x of the previous one). It is easy to see that

the successive derivatives of this function satisfy the require condition, and the last property

follows from the construction.

Now let (a

)

n∈N

be an arbitrary sequence of real numbers. For all n ∈ N, one can apply the

previous construction to ﬁnd Ψ

such that

sup

x∈[−1,1]



(n−1)

(x)



·max(1, |a

It is then immediate that the series

converges uniformly to a function f having all

desired properties.

Of course, the function f thus constructed is by no means unique: one may add a term

α(ϕ

′

−1), where α ∈ R, without changing the values of the derivatives at 0.

 Solution of exercise 1.12. Let

(x) = −

4n−1

(4n −1)!

4n+1

(4n + 1)!

for n ¾ 1; the se ries

converges to F (x) = sin x − x.

 Solution of exercise 1.13

i) The power series for f (a + r e

iθ

) may be integrated term by term because of its absolute

convergence in th e disc centered at a of radius r < R. Since we have

2π

i(k−n)θ

dθ = δ

1 if k = n,

0 otherwise,

the stated formula follows.

Solutions of exercises 49

ii) Similarly, expand



f (a + r e

iθ

)



as a product of two series and integrate term by term.

Most contributions cancel out using the formula above, and only th e terms |c

remain.

iii) If f is bounded on C, we have |c

| ¶ kf k

∞

. Letting r → +∞, it follows that c

= 0

for n ¾ 1, which means that f is constant.

iv) The function sin is not bounded on C! Indeed, we have for instance lim

x→+∞



sin(ix)



+∞. So there is no trouble.

 Solution of problem 1

i) (a) Let x ∈ I. For any p, q ∈ N, we have



(x) − f

(x)



¶ sup

y∈I



( y) − f

( y)





− f



∞

and this proves that the sequence



(x)



n∈N

is a Cauchy sequence in R, so it

converges.

(b) Let ǫ > 0 be ﬁxed. There exists N such that



− f



∞

¶ ǫ for all p > q > N .

Let x ∈ I. We then have



(x) − f

(x)



¶ ǫ for any p > q > N ,

and since this holds for all p, we may ﬁx q and let p → ∞. We obtain



f (x) − f

(x)



¶ ǫ for all q > N .

This bound holds independently of x ∈ I. Thus we have shown t hat



f − f



∞

¶ ǫ for any q ¾ N.

Finally, this being true for any ǫ > 0, it follows that the sequence ( f

)

n∈N

converges uniformly to f .

Remark: At this point, we haven’t proved that there is convergence in the norme d

vector space



E, k·k

∞



. It remains to s how that the limit f is in E, that is, that f is

continuous. This follows from Theorem 1.33, but we recall the proof.

Let ǫ > 0 be ﬁxed. From the preceding question, there exists an integer N

such that kf

− f k

∞

¶ ǫ for all n ¾ N , and in particular kf

− f k

∞

¶ ǫ.

Since f

is an element of E, it is continuous. So there exists η > 0 such that

∀y ∈ I |y − x| ¶ η =⇒



( y) − f

(x)



¶ ǫ.

Using the triangle inequality, we deduce from this t h at for all y ∈ I such that

|x − y| ¶ η, we have



f ( y) − f (x)



f ( y) − f

( y)



( y) − f

(x)



(x) − f (x)



¶ 3ǫ.

This proves the continuity of f at x, and since x is arbitrary, this proves th at f

is continuous on I, and hence is an element of E.

(d) For any Cauchy sequence ( f

)

n∈N

in E, the previous questions show that ( f

)

n∈N

converges in E. Hence the space



E, k·k

∞



is complete.

ii) Let f be a ﬁxed point of Φ. Then we have

∀t ∈ I f

′

(t) =



Φ( f )



′

(t) =

t f (t)

1 +



f (t)



Moreover, it is easy to see that f (0) = Φ( f )(0) = 1.

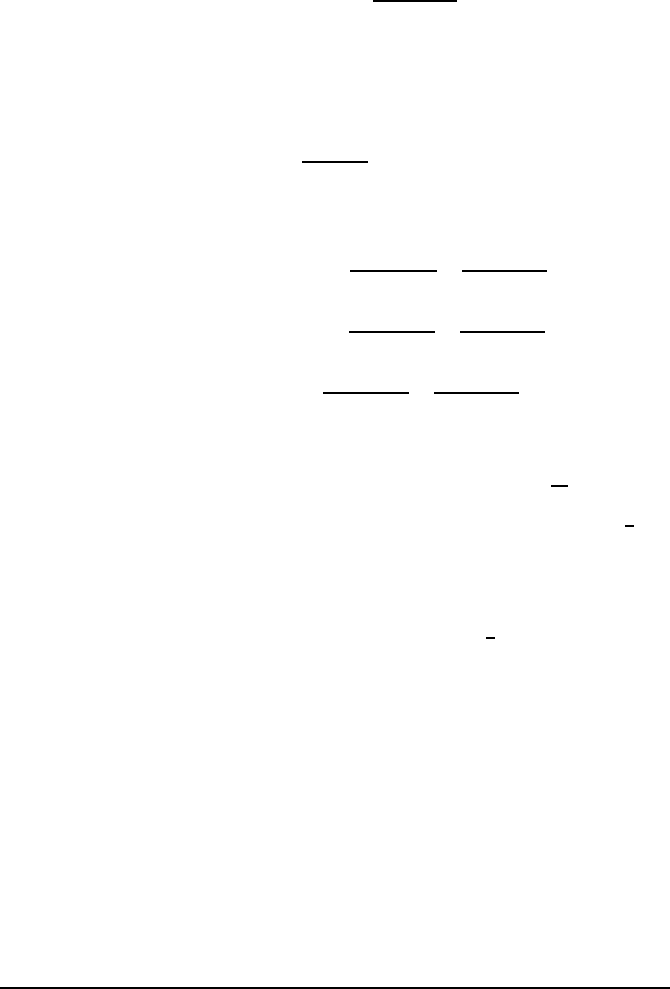
50 Reminders concerning convergence

Conversely, le t f be a solution of the Cauchy problem (E) + (C I). Then Φ( f ) is

differentiable and we have

∀t ∈ I Φ( f )

′

(t) =

t f (t)

1 +



f (t)



= f

′

(t).

The functions f and Φ( f ) have the same derivative on I, and moreover satisfy

Φ( f )(0) = 1 and f (0) = 1.

It follows that Φ( f ) = f .

iii) Looking at the derivative g

′

: x 7→

1 − x

(1 + x

)

we see that



′

(x)



¶ 1 for all x ∈ R. The

mean-value theorem then proves that g is 1-Lipschitz, as stated.

iv) Let f , g ∈ E. Then we have



Φ( f ) −Φ(g)



∞

= sup

t∈I



u f (u)

1 +



f (u)



−

u g(u)

1 +



g(u)





¶ sup

t∈I



f (u)

1 +



f (u)



−

g(u)

1 +



g(u)





f (u)

1 +



f (u)



−

g(u)

1 +



g(u)





by po sitivity. Using the inequality of the previous question, we get



Φ( f ) −Φ(g)



∞



f (u) − g(u)



du ¶ kf − gk

∞

u du =

kf − gk

∞

This is true for any f , g ∈ E, and hence Φ is (a

/2)-Lipschitz; if 0 ¶ a <

2, this

map Φ is a contraction.

v) According to the ﬁxed-point theorem, the previ o u s results show that Φ has a unique

ﬁxed point in E.

According to Question ii), this means that there exists a unique solution of the

Cauchy Problem (E) + (C I) on an interval [0, a] for a <

To approximate the solution numerically, i t is possible to select an arbitrary funct ion

(for instance, simply f

= 0), and construct the sequence ( f

)

n∈N

deﬁned by f

n+1

Φ( f

) for n ¾ 0. This requires computing (numerically) some integrals, which is a fairly

straightforward matter (numerical integration is usually numerically stable: errors do

not accumulate in general

). The speed of convergence of the sequence ( f

)

n∈N

to the

solution f of the Cauchy problem is exponential: with I = [0, 1], the distance (from

the norm on E) between f

and f is divided by 2 (at least) af ter each iterative step. It

is therefore possible to expect a good numerical approximation after few iterations (the

precision after ten steps is of the order of kf

− f k

∞

/1000 since 2

= 1024).

On the other hand, numerical differentiation tends to be much more delicate.

Chapter

Measure theory and the

Lebesgue integral

This chapter is devoted to the theory of integration. After a sur vey of the Riemann

integral and a discussion of its li mitations, we present the Lebesgue integral. This re-

quires a brief discussion of basic measure theory, which is important for probability

theory as well.

Note that the main theorems and techniques of integral calculus (change of vari-

able, justiﬁcation of exchanges of l imits and integrals) are discussed in the next

chapter.

2.1

The integral according to Mr. Riemann

2.1.a Riemann sums

One poss ible way of deﬁning the integral of a function f on a ﬁnite interval

[a, b] is the following: start by subdividing th e interval in n parts, which are

more or less of the sa me size ≈ (b −a)/n , by choosing real numbers

a = x

< x

< ··· < x

= b ;

52 Measure theory an d the Lebesgue integral

a = x

··· ··· x

n−1

= bx

k+1

Fig. 2.1 — The interval [a, b] is here partitioned uniformly, with n subintervals of constant

length (b −a)/n.

then “approx imate” the function f by a “step” function which is constant on

each interval of the subdivision, and takes there the same value as f at the

beginning of the interval:

The sum of the areas of the small rectangles is then equal to

k=1

− x

k−1

) · f (x

k−1

and it may be expected (or hoped) that as n goes to inﬁnity, this value will

converge to some limit. Riemann’s result is that this happens if the approxi-

mations used for f improve steadily as n increases. Th is means th at the values

taken by f on an interval [x, x + ǫ] must be very close to f (x) when ǫ is

small. T his is a continuity assumption for f . Here is the precise result.

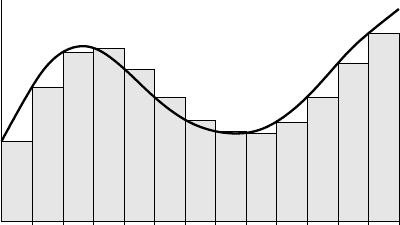
DEFINITION 2.1 (Subdivision) A subdivision of the interval [a, b] is any tu-

ple of real numbers of the type

= (x

)

i=0,...,n

where a = x

< x

< ··· < x

= b.

The step of the subdivision σ

is the length of the largest subinterval:

π(σ) = max

i∈[[0,n−1]]



i+1

− x



A marked subdivision of [a, b] is a pair

′



)

i=0,...,n

, (ξ

)

k=1,...,n



where (x

)

i=0,...,n

is a subdivision of [a, b] and ξ

∈



k−1

, x



for all k.

DEFINITION 2.2 (Riemann sums) Let σ

′



)

, (ξ

)



be a marked subdi-

vision of [a, b] and let f : [a, b] → K be a function with values in K = R

The integral according to Mr. Riemann 53

or C. The Riemann sum of f associated to σ

′

S( f , σ

′

) =

k=1

− x

k−1

) · f (ξ

The following result provides a rigorous deﬁnition of th e integral of a

continuous function on a ﬁnite interval:

THEOREM 2.3 (and deﬁnition of the integral) Let f : [a, b] → K be a contin-

uous function. For any sequence (σ

′

)

n∈N

∗

of marked subdivisions of [a, b], such that

the step of the subdivisions tends to 0 as n tends to inﬁnity, the sequence of associated

Riemann su ms converges. Moreover, the limit of this sequence is independent of the cho-

sen sequence of marked subdivisions. The (Riemann) integral

of the function f is

deﬁned to be this common limit:

f (x) dx =

f = lim

n→∞

S( f , σ

′

)

where (σ

′

)

satisﬁes lim

n→∞

π(σ

′

) = 0.

This result and deﬁnition may easily be extended to piecewise continuous

functions,

and to even larger classes of functions, by means of a small change

in the construction used . Namely, deﬁne a step function on [ a, b] to be a

function ϕ which is constant on th e subintervals of a subdivision

σ = (a

, . . . , a

)

of [a, b]. The integral of a step function ϕ associated to σ and taking the

value y



i−1

, a



is obviously equal to

ϕ =

i=1

−a

i−1

) y

For any function f : [a, b] → R, deﬁne

−

( f ) = sup

Z

ϕ ; ϕ step function with ϕ ¶ f



The notation “d” for differentiation, “dy/dx”, “

” (which originally represented an “s,”

the initial of summa), are due to Gottfried Leibniz (1646—1716), who also invented the name

“function” and popularized the use of the equal sign “=” and of a dot to represent multipli-

cation. Joseph Fourier (1768—1830) invented the notation “

”.

Recall that f : [a, b] → K is piecewise continuous if there exist an integer n and real

numbers

a = a

< a

< ··· < a

= b

such that, for all i ∈ [[0, n −1]], the function f restricted to



, a

i+1



is c o ntinuous and has

ﬁnite limits as x tends to a

from above, and to a

i+1

from below.

54 Measure theory an d the Lebesgue integral

and

( f ) = inf

Z

ϕ ; ϕ step function with ϕ ¾ f



Then f is integrable in th e sense of Riemann, or Riemann-integrable, if

we have I

−

( f ) = I

( f ).

A more delicate is sue is to extend the deﬁnition to functions which are

deﬁned on an ar bitrary interval (not necessarily closed or bounded), such as

]α, β] or [α, +∞[.

2.1.b Limitations of Riemann’s deﬁnition

• Some easily deﬁned functions cannot be approximated by step func-

tions, and the Riemann sums for those functions do not converge

to a common value. This is the case, for instance, for the function

d : [0, 1] → R, which is deﬁned by d(x) = 0 if x is irrational, and

d(x) = 1 if x is rational. This function is therefore not Riemann-

integrable.

• The deﬁnition turns out to be t he very devil to deal with as soon as

questions of convergence of sequences of integrals appear. In particular,

to justify that the integral of the sum of a series is the sum of the series

of integrals, one needs very stringent conditions.

• It also turns out that if we want to deal with a complete space of func-

tions with the norm

|f (t)|dt, not even th e most liberal deﬁnition

of Riemann integral is sufﬁcient. The smallest complete space con-

taining C ([a, b]) is much larger than the space of Riemann-integrable

functions; it is the space L

deﬁned in the next s ection.

2.2

The integral according to Mr. Lebesgue

To solve the problems related to Riemann’s deﬁ nit ion of integrable func-

tion, the idea is to provide an alternate deﬁnition for which a much larger

class of functions will be integrable.

In particular, this s pace of integrable

functions, denoted L

, will turn out to be complete.

From the point of view of trying to obtain a complete space with the norm

kf k



f (x)



dx,

it is always possible to “complete” a metric space, in p articular, a normed vector space; more

precisely, given a normed vector space



E, k·k



, there e xists a complete normed vector space



F , k·k

′



such t h at E is isometric to a dense subspace E

′

of F . Using this isometry, E may

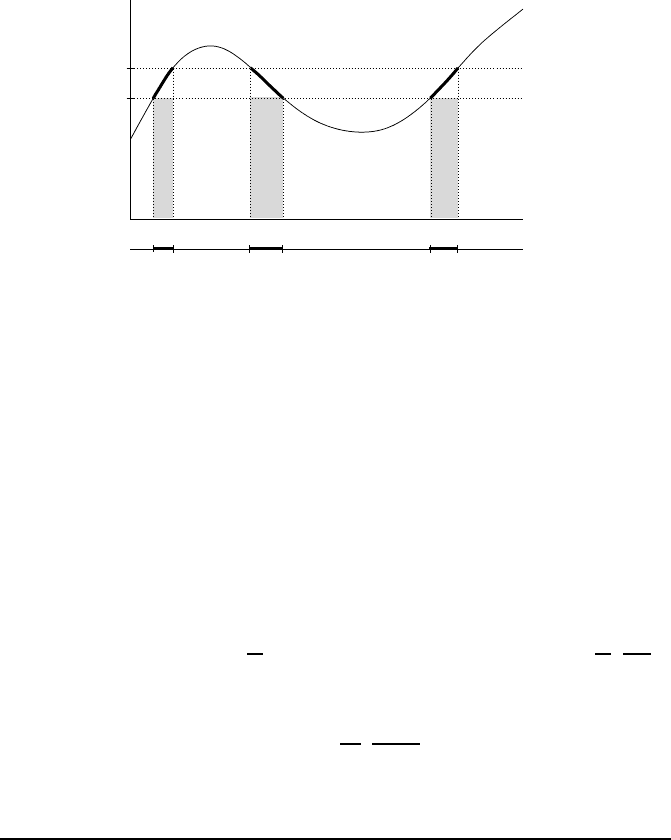
The integral according to Mr. Lebesgue 55

(n)

k+1

Fig. 2.2 — Co nstruc tion of the sets A

(n)

= f

−1



, x

k+1



, where x

= k/2

, with the

value of µ



(n)



·k/2

2.2.a Principle of the method

Lebesgue’s idea to deﬁne the integral of a real-valued function is t he following:

for various possible values (denoted α) of the function, we consider the “size”

of the set of points wh ere f takes the value α (or is suitably close to α). Mul-

tiply the size of this set by α, and repeat with other values, tallying the total

sum t hus obtained. Taking a limit in a suitable manner, this sum converges

to the integral of the function.

In other words, instead of a “vertical” dissection as in R iemann’s method,

one has to perform an “horizontal” dissection a s follows. Assume ﬁrst that

f takes non-negative values. Subdivide the set R

of values in inﬁnitely

many intervals, say of size

. For each subinterval of the type



k+1



consider t he set of real numbers x such tha t f (x) belongs to this interval (see

Figure 2.2):

(n)

= f

−1



k + 1



Denote by µ



(n)



the “size” of this set (temporarily ; this crucial notion

be seen as a dense subspace o f a complete space. The general constructi o n of F is somewhat

abstract (F is the set of Cauchy sequences in E, modulo the equivalence relation u ∼ v, if and

only if u −v is a sequence converging to zero), but it is very powerful. In particular, it p rovides

one construction of the set R of real numbers, starting with Cauchy sequences in Q.

Henri Lebesgue used the following analogy: to sum up a certain amount of money, we can

— instead of adding up the values of all coins as th ey come up one by one — start by putting

together all dimes, all nickels, all $1 bills, and then count the number of each stack, multiply

it by the common value of each coin or bill in the st ack, and ﬁnally add up everything.

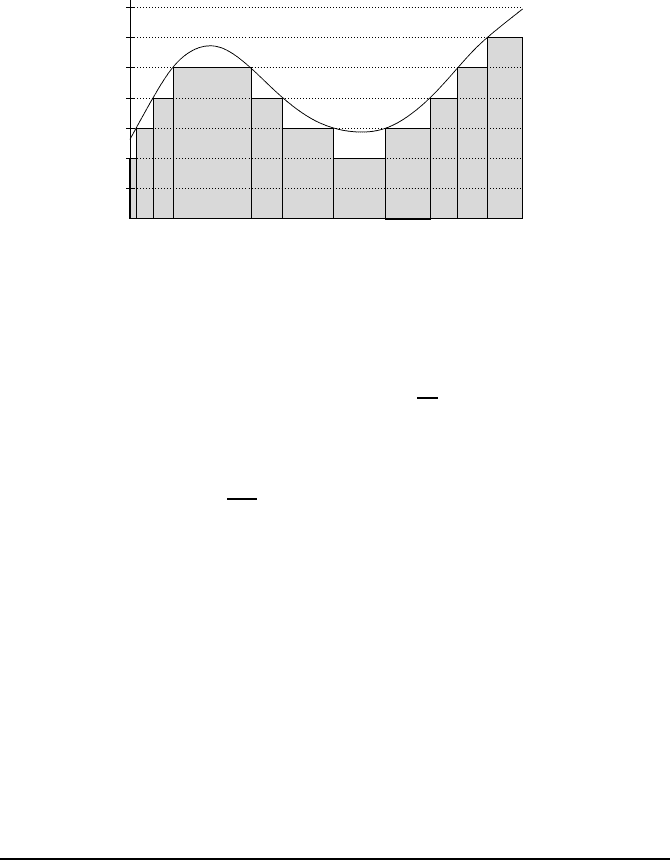
56 Measure theory an d the Lebesgue integral

Fig. 2.3 — Construction o f the integral of f .

of “size” will be mad e precise later), and then deﬁne

( f ) =

∞

k=0



(n)



It is quite easy to check that the sequence



( f )



is increasing (see Fig-

ure 2.4).

Hence it converges in R

= R

∪ {+∞}, and the limit is denoted

f .

The function f is said to be integrable (in the sense of Lebesg ue) if the limit

is ﬁnite.

This is the principle. As can be seen, the issue of evaluating the “size” of

the sets A

(n)

has been left open. This very important point is the subject of

the next sections.

Remark 2.4 Before going farther, we brieﬂy explain what is gained from this new method:

• the set of integrable functions i s vast, be yond human imagination;

• the set of Lebesgue -integrable functions (not yet precisely deﬁned), denoted L

or, to be

precise, L

(R) or L

[a, b ], is complete for the norm kf k =

|f |;

• the theorems of the Lebesgue integral calculus are inﬁnitely si mpler and more powerful

(in particular, concerning the inversion of limits and integrals, or differentiation under

the integral sign), even when applied to very regular functions.

The exac t deﬁnition below will be slightly different, but equivalent; it will not involve a

partic u l ar choice of intervals (bounded by numbers of the form k/2

) to subdivide R

Much larger than the set of Riemann-integrable functions, in parti cular, because even very

irregular functions become integrable. It is t rue that some Riemann-integrable functions are

not Lebesgue integrable, and that this causes trouble, but they are typically functions which

create all the difﬁculties of the Riemann theory.