Алешин Г.В. Оценка качества информационно-измерительных систем
Подождите немного. Документ загружается.


81
∂
ψ
o
- ошибка, сглаженная системой ФАПЧ;
2
0
Τ
=Z
- энергия сигнала без потерь;
f(ТП
фнч
) - относительные потери энергии за счет не идеальности интегри-
рования;
П
фнч
- полоса фильтра нижних частот.
В (3.56) показано, что вкладом в δt за счет нестабильности существующих
стандартов частоты можно пренебречь и ошибка канала синхронизации δt обу-
славливается в основном движением подвижных объектов и астатизмом канала
синхронизации. Поскольку для реальных сигналов и параметров движения объ-
ектов произведение
( )
1−
∋
τ
kk
R
(k-й производной от дальности на
1−
∋
τ
k
) быстро
убывает, ряд (3.97) быстро сходится и в первом приближении следует ограни-
читься лишь R
(1)
.
Тогда δt
∂
из (3.130) определится как
( )
C
NR
t
2
1
∆
τ=δ
∋∂
.
При этом в предположении, что синхронизация осуществляется путем из-
менения тактовой частоты F
T
(R), определяется разность величины максималь-
ной скорости объекта и того ее значения, которое еще отслеживает канал син-
хронизации:
( )
( )
RmaxF
RmaxF
cmaRR
T
T
∋
τ
−=∆
Таким образом, при корреляционной обработке ШШС на формировании
функции неопределенности (выходного сигнала) сказываются расстройки и не-
идеальности приемника.
При этом необходимо отметить следующее.
1. Выходной эффект как многомерная функция расстроек и неидельности
может быть представлен в факторизованном виде (в виде произведений одно-
мерных функций от расстроек и неидеальностей).
2. Функции от расстроек и неидеальностей имеют монотонный характер.
3. Условие обеспечения, необходимого уровня Z
1
(3.I30) предъявляет более
жесткие требования к расстройке и неидеальности, чем сделанные допущения
об их малости, т.е. для того, чтобы при
α
λ
≥>α
0
1
Z
Z
I
необходимо, чтобы, при
равном вкладе в потери выходного эффекта
( )
α
−≤ψ
α
−≤
τ
δ
α
−≤ϕ
∋
∂
1
12
1
1
1
1
0
51
,
t
,a
,
82
5
51
51
12
5
6
≥
−
∂
α≤Π
α−
≤ω
a
фнч
lnT,
T
например, при α=2
( )
.,T;
T
,
,,;
,
t
;,aI
фнч
o
090
480
438010501050
2
<Π≤ω
≤ψ≤
τ
δ
≤
∂
∂
∋
∂
4. Самые жесткие требования предъявляются к полосе пропускания фильт-
ра нижних частот и расстройке ω
∂
по частоте и самые слабые - к дисперсии
суммарной фазовой ошибки
2
∂
ψ
o
.
ВЫВОДЫ
В результате рассмотрения влияния рассмотренных аффектов на корреля-
ционную обработку сигнала можно сделать следующие выводы.
1. Ограничение результирующей полосы высокочастотного тракта от пе-
редатчика до перемножителя приемника приводит к постоянной задержке
(3.54), связанной с длительностью переходных процессов, потерям анергии и к
незначительным искажениям свертки принимаемого и опорного сигналов. По-
стоянное запаздывание учитывается в канале синхронизации, поэтому при оп-
тимизации системы следует учитывать лишь потери уровня выходного эффекта
(3.65) в за висимости от отношения α результирующей полосы высокочастот-
ного тракта к ширине спектра широкополосного шумоподобного сигнала
(ШШС).
2. В режиме автосопровождения по углам флуктуации максимума суммар-
ной диаграммы направленности антенны при моноимпульсном методе вокруг
направления на объект приводят к средним потерям мощности сигнала, зави-
сящим от отношения α ширины диаграммы по мощности к дисперсии устано-
вившейся ошибки сопровождения по углам. Потери существенны уже при α≤8.
3. При условии устойчивого слежения системой ФАПЧ за расстройкой по
частоте эффект Допплера сильнее сказывается на потерях энергии за счет изме-
нения тактовой частоты (длительности элементов) и слабее за счет изменения
несущей частоты. Поэтому взаимная связь тактовой и несущей частоты для оп-
ределения потерь при данное эффекте значения не имеет, играет роль лишь ди-
намическая ошибка слежения за частотой, астатизм фильтра и соответственно
величина радиальной скорости и ее производных. Потери энергии значительно
растут (3.97) с увеличением количества элементов, с уменьшением порядка ас-
татизма и при сложном движении объекта с большей величиной производных
высших порядков.

83
4. Потери энергии выходного сигнала растут пропорционально кратковре-
менной нестабильности тактовой частоты и корню квадратному из количества
элементов ШШС (3.107). Однако лишь для большего количества элементов
ШШС (N≥10
10
) и значительных шумов при простых средствах стабилизации
тактовой частоты
≈
∆
−5
10
T
T
F
F
потери энергии могут быть ощутимыми.
5. При большом количестве элементов ШШС и относительно малых дина-
мических ошибках отслеживания частоты в канале синхронизации потери энер-
гии за счет эффекта Допплера и нестабильности частоты имеют сложную зави-
симость (3.112). Однако при современных стандартах частоты, малых шумах в
канале синхронизации и применяемом количестве элементов практически сле-
дует считаться лишь с потерями энергии за счет суммарных ошибок, включая
динамические при наличии сложного движения объекта и недостаточного по-
рядка астатизма какала синхронизации.
6. Для малых расстроек по частоте и по временной задержке выходной
сигнал (функцию неопределенности) можно представить в виде произведения
одномерных функций от аргументов, характеризующих расстройки и неидеаль-
ности (3.130), что важно при формализации задач оптимизация систем, исполь-
зующих ШШС.
7. Результаты раздела могут оказаться полезными для следующих инже-
нерных расчетов:
а) для расчета влияния
ограниченной полосы пропускания на величину
выходного фазоманипулированного по закону псевдослучайной последова-
тельности сигнала при различных расстройках в канале синхронизации и раз-
личных коэффициентах знаковой автокорреляции ПСП (при расстройке на дли-
тельность элемента);
б) для расчета потерь энергетического потенциала при простpaнственных
флуктуациях диаграммы направленности антенны в режиме автосопровожде-
ния по углам, для расчета соответствующего распределения уровня сигнала и
моментов, распределения для определения оптимального соотношения между
дисперсией ошибки автосопровождения по углу и направленностью антенны,
что позволяет достичь максимальной дальности радиолинии;
в) для расчета потерь энергий сигнала за счет движения объекта при кор-
реляционной обработке сигнала и слежения за задержкой с динамическими
ошибками; получены рекуррентные соотношений для расчета максимально до-
пустимого количества элементов ФМ ПСП сигнала при худшем ожидаемом за-
коне движения;
г) для расчета потерь анергии сигнала за счет нестабильности тактовой
частоты в канале синхронизации; для расчета максимально допустимого коли-
чества элементов сигнала при заданной нестабильности тактовой частоты кана-
ла синхронизации;
д) для расчета потерь энергии сигнала за счет одновременного влияния ди-
84
намических ошибок канала синхронизации и худшего возможного движения
объекта и нестабильности тактовой частоты;
е) для расчета потерь энергии сигнала за счет влияния ошибки синхрони-
зации с нормальным распределением;
ж) для расчета потерь энергии сигнала при корреляционной обработке за
счет одновременного влияния расстроек и неидеальностей;
з) для оценки требований к расстройкам и неидеальности при заданных
потерях энергии.
Рассмотренными в разделе эффектами далеко не ограничивается список
факторов, которые следует учесть при синтезе РТС. Автор счел уместным при-
вести лишь результаты, которые менее всего освещены в литературе.
85
РАЗДЕЛ 4
ПАРАМЕТРИЧЕСКИЙ СИНТЕЗ
ИНФОРМАЦИОННО-ИЗМЕРИТЕЛЬНЫХ СИСТЕМ
4.1. Показатели качества радиотехнических систем
В разделе 2 показано, что наиболее объективным критерием оптимальности
можно считать условный критерий, учитывающий совокупность показателей ка-
чества, представленных в ТТТ.
К современным радиотехническим системам предъявляют множество таких
тактико-технических требований (ТТТ), выполнение которых обеспечивает соз-
данной системе успешное функционирование и решение поставленных задач. К
основным показателям качества РТС, которые так или иначе учитываются при
проектировании, прежде всего следует отнести:
1. Точность измерений параметров движения объекта.
2. Помехоустойчивость передачи информации прямого и обратного каналов.
3. Точность сверки времени и привязки шкал.
4. Время измерений и передачи информации.
5. Надежность функционирования.
6. Электромагнитная совместимость.
7. Скорость передачи информации.
8. Пропускная способность системы.
9. Живучесть.
10. Помехозащищенность.
11. Экономичность.
12. Вес аппаратуры и ее составных частей.
13. Объем аппаратуры и ее составных частей.
14. Прочие показатели качества.
При оптимизации РТС на этапе проектирования, а также для оценки указан-
ных показателей качества удобней выражать их в конкретной числовой форме в
виде вектора, достаточно полно описывающего качество выполнения основной
задачи. Вектор приведенных выше качественных показателей можно использовать
для оптимизации любых РТС. Показатели качества являются взаимосвязанными и
взаимообусловленными. Поэтому более полный их учет приводит принятую мо-
дель системы в большее соответствие с реальной РTC. В этом свете решение зада-
чи оптимизации по критериям 1-14 равноценно глобальному решению при фикси-
рованных значениях 13 независимых критериев или нулевому приближению при
наличии связей между критериями.
86
В разделе сформулирована и решена задача оптимизации однопараметриче-
ской измерительной системы по критерию минимума ошибки измерения парамет-
ра движения ЛА при ограниченных ассигнованиях на систему. В данном разделе
будет формализована и решена задача оптимизации систем на множестве техниче-
ских, сигнальных и структурных параметров, т.е. задача параметрического синтеза
систем с учетом основных критериев.
Идею оптимизации в упрощенном виде можно изложить следующим обра-
зом. Предполагается, что имеется корреляция либо функциональная зависимость
между основными техническими параметрами и стоимостью системы, т.е., что при
улучшении качества стоимость системы, вообще говоря, монотонно увеличивает-
ся. Например, при увеличении мощности либо при уменьшении нестабильности
частоты стоимость системы возрастает. Заданные требования к качественным по-
казателям системы являются ограничениями на те технические параметры, от ко-
торых зависят эти качественные показатели. Например, ошибка передачи инфор-
мации либо измерений параметров движения зависит от отношения сигнал/шум на
выходе каналов. В свою очередь отношение сигнал/шум зависит от таких техниче-
ских параметров, как мощность передатчика, коэффициент усиления антенны, ко-
эффициент шума приемника и т.д.
Если для системы использовать предельные, самые лучшие, технически реа-
лизуемые значения всех параметров, то стоимость такой системы будет чрезвы-
чайно большой и вряд ли оправданной. К показателям качества РTC, работающих
на малых дальностях не предъявляют высоких требований, поскольку реализация
предельных значений параметров представляет собой научно-техническое дости-
жение и требует самых высоких и поэтому неоправданных ассигнований, кроме
того улучшение параметров незначительно и мало сказывается на качественном
показателе.
Даже при слабых требованиях к качественным показателям системы далеко
не все равно, какие технические показатели выбирать. Если один из технических
параметров выбирать технически реализуемым, то суммарные расходы на систе-
мы могут существенно возрасти, в то время как качественные показатели изменят-
ся не существенно. Например, если взять предельный коэффициент усиления ан-
тенны, это потребует дополнительных ассигнований на антенну за счет ассигно-
ваний на передатчик и другие блоки, что позволит снизить мощность передатчика
и другие параметры. Но произведение мощности передатчика на коэффициент
усиления антенны должно при этом уменьшиться при тех же ассигнованиях на
обеспечение этих параметров. То же случится при предельной мощности передат-
чика. Поэтому очевидно, что существуют оптимальные значения параметров, при
которых достигается максимальное отношение сигнал/шум при заданных ассигно-
ваниях на систему. Задача синтеза параметров состоит в том, чтобы найти этот
минимум и значения оптимальных параметров системы и всех ее каналов.
87
4.2. Стоимость блоков системы как ограничение на соответствующие
технические параметры
В условиях ограниченности ассигнований на создание этой системы большое
значение имеет оптимальное распределение средств, отпущенных на создание
РТС, которое обеспечивает наивысшую точность измерителя при заданных затра-
тах. Действительно, при современном состоянии науки и техники наивысшая точ-
ность может быть реализована лишь системой, которая имеет предельно лучшие
параметры. Однако стоимость системы значительно возрастает по сравнению с
чуть менее точными, так как предельное значение каждого параметра является со-
временным научно-техническим достижением. Очевидно, что стоимость имеет ту
же значимость, что и точность.
Стоимость системы зависит от времени, номера серии, года выпуска и т.д., а
период "морального старения" техники соизмерим со сроком службы. Однако
стоимость системы неизменна на соответствующем достаточно коротком интер-
вале времени постепенного эволюционного развития техники и производства и
может быть пересчитана к моменту готовности изделия к сборке. При революци-
онном развитии техники и производства, т.е. при изобретении новых элементов,
принципов работы аппаратуры, методики измерений, способов производства, оп-
тимальность технических параметров меняется, поскольку как стоимость системы,
обеспечивающая при правильной реализации системы заданную ошибку измере-
ния, так и собственно погрешность измерений при ограниченной стоимости реа-
лизации системы может существенно меняться. Потребность в оптимизации тем
более необходима, если оптимизируемые измерители для больших дальностей яв-
ляются сложными системами большой стоимости, на которых одни и те же рево-
люционизирующие факторы сказываются в меньшей степени, чем на малых сис-
темах. Кроме того, подобная аппаратура может быть уникальной и малосерийной.
Последнее обстоятельство свидетельствует о том, что в этом случае затрудняется
или совсем исключается обычная оптимизация аппаратуры за счет серийности
производства, рассчитанная на здоровую инженерную интуицию (метод "проб и
ошибок").
При этом в зависимости от того, какие элементы и узлы использует завод-
изготовитель системы, будем считать, что статистика себестоимостей этих эле-
ментов и узлов взята на соответствующих заводах-поставщиках.
Постановка задачи оптимального построения системы для измерения ради-
альной скорости по критерию качества состоит в том, что в виде многомерной це-
левой функции, выражающей точность измерения частоты Доплера и зависящей
от расстроек и неидеальностей системы, формализуются требования к узлам, бло-
кам системы, которые приобретают определенный смысл (решение) лишь при на-
88
личии ограничений и связей между параметрами.
В технике всегда имеется диалектическое противоречие между техническими
параметрами системы, описывающими качество соответствующих блоков, и
стоимостью разработки и производства соответствующей части системы. Причем,
улучшая технические характеристики, мы вынуждены соответственно увеличи-
вать ассигнования на систему.
Как показано в литературе [39, 40], между параметрами системы и ее стоимо-
стью существует высокая корреляция, либо даже известная функциональная зави-
симость. Это дает основания установить характер зависимости технических пара-
метров системы от ее стоимости как ограничений и искать глобальный экстремум
целевой функции. Решение же задачи позволяет найти не только оптимальное
распределение средств между блоками, но и оптимальные технические параметры
РТС, которые определяют оптимальный в этом смысле выбор блоков при проек-
тировании системы.
Оптимизация РТС измерения радиальной скорости производится по крите-
рию точности, вычисляемой дискриминаторным методом в режиме автосопрово-
ждения, поэтому синтез поисковых и других систем должен осуществляться ана-
логично с учетом других критериев, например, максимальной вероятности обна-
ружения сигнала при заданном времени поиска при заданной вероятности обна-
ружения и т.п.
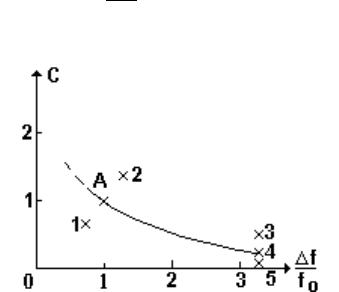
Для случая, когда задача решена, выбор решения проиллюстрируем (рис. 4.1)
на примере зависимости среднеквадратического значения стоимости стандартов
частоты, используемых в качестве задающего генератора (ЗГ), от кратковремен-
ной (за 1 с) нестабильности частоты
∆f
fo
.
Рис. 4.1
Пусть точки 1-5 соответствуют определенным современным стандартам час-
тоты, а зависимость C=C(
∆f f
зг
/
0
) может быть определена следующим образом.
Кривая С есть кривая среднеквадратической регрессии стоимости от пара-
метра относительной нестабильности частоты, полученная путем сглаживания из-
89
вестных значений параметров для известных образцов (стандартов). Неполная эк-
вивалентность стандартов частоты может объясняться различиями весов, объемов,
эксплуатационными условиями, способами определения себестоимости, техноло-
гическими условиями и т.д. Если в результате оптимизации обнаружено, что оп-
тимум точности системы достигается в точке А, то следует выбрать тот стандарт,
который обеспечивает лучший параметр (например, 1 или 2 в зависимости от дру-
гих качеств: надежности, удобства в эксплуатации, объема и т.д.).
Если выбран стандарт 1, то при дальнейшем проектировании и разработки
целесообразно снижать требования к параметру и улучшать другие показатели
так, чтобы стоимость была не большей стоимости в точке А. Когда снизить требо-
вания нельзя, следует ограничиваться выбором стандарта, близкого к оптималь-
ному.
В случае, когда большая стоимость достигается не за счет улучшения качест-
ва стандарта (точка 2), при расчете кривой ее не следует учитывать.
Если попытаться определять оптимум целевой функции для набора реализа-
ций параметра (таких, как точки 1-5), то легко обнаружить, что процедура поиска
оптимума путем перебора комбинаций реализаций для всех ограничений резко
усложняется с ростом размерности задачи и числа реализаций этого параметра.
Действительно, при числе реализаций i-го параметра m
i
, и числа параметров
Nc системы количество вычислений целевой функции при заданных значениях
параметров и количество сравнений по величине равно М =
m
i
i
N
=
∏
1
. Например, при
m
i
=m>10 и Nc>14 M>IO
14
. Если время счета целевой функции равно 1 мкс, то не-
обходимость вычислений пропадает, так как требуется более 10 лет непрерывного
счета. Поэтому представление ограничений по стоимости на параметры в виде не-
прерывных функций среднеквадратической регрессии является лучшим в этих ус-
ловиях способом формализации задачи.
Стоимости Сi блоков системы зависят не только от требуемых Ji, а также от
других критериев, например, надежности, долговечности, веса и т.п. Поэтому Сi
должны определяться при возможно равных условиях и одинаковом назначении
блоков.
Стоимость в процессе оптимизации системы есть многомерная функция рег-
рессии всех фазовых параметров, которые характеризуют расстройки, неидеаль-
ности и другие технические параметры блоков системы, т.е., стоимость представ-
ляет собой выборочное математическое ожидание ансамбля стоимостей при фик-
сированных значениях фазовых параметров и минимальных среднеквадратиче-
ских отклонениях.
Как и любую непрерывную и гладкою функцию, имеющую производные
многих порядков, ее можно представить в виде ряда Тейлора в окрестности точки

90
(X
10
, ..., Xi0)
С Х X C X X C X X
C X
X X X
l l i i i
i
l
i i i j j
ij
l
( ,..., ) ( ,..., ) ( )
( )( )
...,
1 10 0 0 0
1
0 0 0
1
2
= +
′
− +
+
′′
− − +
=
∑
∑
где
′
= =
′′
= = =C
C
X
X X C
C
X X
X
X X X
i
i
i i i
i j
i i j j
0 0 0
2
0 0
∂
∂
∂
∂ ∂
/ ,
/ , .
Коэффициенты разложения можно найти методом наименьших квадратов.
Чем больше выборочных значений С и лучше их группирование вокруг матема-
тического ожидания, тем меньше неопределенности в объективном законе зави-
симости стоимости от фазовых параметров.
На практике всегда может случиться, что сведений о зависимости стоимости
от каких-либо параметров нет или статистика неудовлетворительна - нет доста-
точного числа выборочных значений при большой дисперсии и нет возможности
ее восполнить и ею воспользоваться. Тогда естественно оптимизировать систему
по остальным параметрам, выбрав такое значение не оптимизируемого параметра,
которое чаще используется в современных системах того же класса. При такой
оптимизации качественный показатель системы скорее всего будет хуже, чем при
полной оптимизации, и тем хуже, когда более значимый параметр исключается.
Вероятное ухудшение качественного показателя системы будет существенней, ес-
ли величины его частотной производной по исключаемому параметру больше, ес-
ли допустимый диапазон этого параметра (диапазон использования) больше и ес-
ли, наконец, степень «угадывания» оптимальности параметра при выборе фикси-
рованного значения хуже. Отсюда следует, что если величина производной по па-
раметру и сам параметр малы, то этот параметр можно исключить, заменив посто-
янным значением. Однако, если таких параметров окажется так много, что они
будут определять существенную часть стоимости иди вносить существенные
ухудшения в качественный показатель, то исключать их нужно корректно.
Как ограничения на параметры, или критерий экономической эффективно-
сти, стоимость обладает преимуществами пo сравнению со многими другими кри-
териями.
Первое преимущество - аддитивность: стоимость системы есть сумма стои-
мостей ее отдельных частей и блоков. Это свойство позволяет во многих случаях
упростить задачу.
Следующее преимущество - "тождество эффекта": посредством стоимости
можно сравнить вклад параметров в показатель качества системы. Стоимость, оп-
