Алешин Г.В. Оценка качества информационно-измерительных систем
Подождите немного. Документ загружается.

61
В) при всех
α
ширина выходного эффекта “по нулям” не меняется;
Г) при всех
α
квазиавтокорреляционная функция близка к автокорреляци-
онной по форме,а при
α
≥
8 - и по величине;
Д) уже при
α
≥
2 квазиавтокорреляционная функция имеет линейный ха-
рактер в сторону опережения принимаемого сигнала;
Е) даже при больших
α
при
δ
t<0 имеет место незначительная кривизна
выходного эффекта, обуславливаемая переходным процессом нарастания на-
пряжения после инверсии фазы на
π
;
Ж) величина квазиавтокорреляционной функции на соответствующем
уровне при любом
α
не больше ширины функции автокорреляции неискажен-
ного сигнала.
На основании (3.65) и приведенных замечаний можно сделать следующие
выводы:
1) при оптимизации системы по параметру
α
следует учитывать потери
энергии сигнала за счет ограниченности полосы пропускания радиотракта до
перемножителя при
α
< 8;
2) смещение квазиавтокорреляционной функции на t
1
в сторону запазды-
вания существенно зависит от
α
, однако при оптимизации его можно учесть
как систематическую погрешность системы синхронизации;
3) из свойств Д) и Е) следует, то при
α
< 8 произойдет дополнительное
смещение опорного сигнала в сторону опережения ввиду кривизны на больших
уровнях автокорреляционной функции, участвующей в создании дискримина-
ционной характеристики канала синхронизации. Это смещение существенно
только при малом отношении сигнал/шум;
4) из свойства Ж) следует, что если при каком-либо
α
компенсировать по-
тери энергии за счет увеличения мощности сигнала и учесть смещение, то каче-
ство оценки задержки и условия разрешения по дальности ухудшатся незначи-
тельно;
5) из свойств А), Г) следует, что при учете смещения квазиавтокорреляци-
онную функцию сигнала в зависимости от параметров
α
и
δ
t можно предста-
вить в виде
( )
[ ]
−
τ
δ
−ϕ−τ=Ζ
∋
∋
a
2lnt
10,a
1N
вых
(3.66)
где
( )
a
e
a2
B
a
2ln
10,a1
a−
+−−=Ι−
.
Поэтому в оптимизации системы могут участвовать факторизованные
функции от параметров а
и
δ
t, если предположить, что систематическая по-
грешность синхронизации ln2/a будет устранена при настройке системы.

62
3.3. Влияние ошибки углового сопровождения антенны на
мощность сигнала и оптимальное соотношение между ее
направленностью и качеством угловой стабилизации луча
Вопрос о влиянии угловой нестабильности антенны и об оптимальном со-
отношении ее направленности к величине ее телесных флуктуаций особенно
остро стоит при создании систем с протяженными радиолиниями, которые ис-
пользуют сигналы большой длительности, например, широкополосные шумо-
подобные сигналы.
Необходимость обеспечения заданного энергетического потенциала ра-
диолинии привела к увеличению коэффициента направленного действия (КНД)
применяемых антенн, а, следовательно, к более жестким требованиям к качест-
ву систем угловой стабилизации антенн.
Вначале рассмотрим для простоты одностороннюю радиолинию, у которой
одна из антенн идеально стабилизирована, а другая - только по одному углу
θ
y
.По другому углу
θ
x
антенна флуктуирует. Пусть дисперсия флуктуаций -
Д
x
. В режиме автосопровождения по этому углу обычно дисперсия флуктуаций
меньше ширины диаграммы направленности антенны по половине мощности.
Для этого случая в окрестности максимума хорошей аппроксимацией диаграм-
мы направленности G(
θ
x
) по полю для реальных антенн может быть закон
G
x
x
x
( ) exp( )θ
θ
= −
2
2
2∆θ
. (3.67)
В случае автосопровождения по углу ввиду многопричинности возмуще-
ний и большой постоянной времени системы стабилизации по углу отклонение
θ
x
(t) максимума диаграммы направленности от направления на цель есть слу-
чайный центрированный стационарный процесс с нормально распределенным
отклонением
p
D
D
x
x
x
x
( ) exp(
)θ
π
θ
= −
1
2
2
2
. (3.68)
Найдем плотность распределения вероятности уровня сигнала по полю
p(G)
p G p
G
x
x
( ) ( )= 2 θ
∂θ
∂
. (3.69)
Поскольку
θ
x x
G
= 2
1
∆θ ln
(3.70)
то
63
p G
G
G
x
( ) /
ln
=
−
α π
α 1
1
(3.71)
где
α
x
x
x
D
=
∆θ
2
.
Семейство
( )
G,
x
αρ
представлено на рис. 3.4. Отсюда математическое ожида-
ние уровня сигнала по полю равняется
[ ]
M G
x
x
=
+
α
α 1
, (3.72)
а n-й начальный момент
[ ]
n
GM
x
x
n
+α
α
=
. (3.73)
Рис. 3.4
Зависимости M[G] и M[G
2
] представлены на рис. 3.5.
Из выражений (3.72, 3.73), а также из рис. 3.5 видно, что учет дестабилизи-
рующих факторов целесообразен уже при
α ≤ 8
, а при
α
x
≈1
он просто необ-
ходим, поскольку при
α
x
= 8
средние энергетические потери составляют 10%,
а при
α
x
=1
- 50%. Очевидно, что с уменьшением
α
x
растет роль мультипли-
кативной помехи за счет флуктуаций диаграммы направленности антенны, ко-
торые имеют распределение (3.71), определяемое формами распределения
флуктуаций и диаграммы направленности антенны.

64
Рис. 3.5
На больших дальностях, когда при оптимальной форме сигнала и макси-
мальной мощности передатчика требуется, кроме того, увеличение КНД антен-
ны, т.е. уменьшение
∆θ
, приходится предъявлять более жесткие требования к
системе угловой стабилизации диаграммы направленности антенны. Точность
исполнения поворотной механической части системы и допуски на флуктуацию
диаграммы направленности антенны также определяются выражениями (3.72,
3.73). При увеличении КНД, усложнении и утяжелении поворотной части ан-
тенны время корреляции уровня сигнала также растет. Формулы (3.72, 3.73)
описывают средние энергетические потери за промежуток времени, превы-
шающий время корреляции.
Максимальная дальность радиолинии R
max
с учетом угловых флуктуаций
при заданном максимальном энергетическом потенциале и параметрах радио-
линии следующим образом зависит от параметра
α
.
Для указанной модели односторонней радиолинии
[ ]
R
P G G
P
M
G
п д п м п д
cп м
п дmax
р р р
р
р
2
0 0
2
2
2
16
=
λ
π
, (3.74)
где P
прд
- мощность передатчика, P
с прм
- реальная чувствительность приемника,
G
0 прд
- КНД передающей антенны, G
0 прм
- КНД приемной антенны,
λ
- длина
волны.
Поскольку КНД антенны
( )
прд0
G
можно представить в виде
2
прдy
2
прдx
прд0
1K
G
θ∆θ∆
=
(3.75)
для остронаправленных антенн, выражение (3.74) с учетом (3.75) запишется
следующим образом (рис. 3.6)
( )
прдx
2
прдx
2
прдx
2
2
max
Д2
K
R
+θ∆θ∆
=
(3.76)

65
где K
1
, K
2
- постоянные;
2
прдy
2
прдx
θ∆θ∆
как и прежде ширина ДН передающей
антенны по полю в идеально и неидеально стабилизированных плоскостях со-
ответственно.
Рис. 3.6
Из (3.76) следует, что зависимость
2
max
R
от
прдx
θ∆
более сильная, чем за-
висимость
2
max
R
от
прдх
Д
Действительно
( )
( )
( ) ( )
( )
( )
( )
2
прдx
2
3
прдx
2
прдx
4
прдx2
прдx
2
max
прдx
2
прдx
2
3
прдx
2
прдx
4
прдx2
2
прдx
2
max
Д2K
Д
R
;ДД2K
R
θθ∆+θ∆−=
∂
∂
+θθ∆+θ∆−=
θ∆∂
∂
−
−
Поэтому всегда
( ) ( )
прдx
2
max
2
прдx
2
max
Д
RR
∂
∂
>
θ∆∂
∂
Таким образом, для увеличения дальности действия командной радиоли-
нии целесообразно преимущественно уменьшать ширину ДН антенны по срав-
нению с ошибкой стабилизации по углу. Если переписать (3.76) в виде
α
−θ∆
=
2
1
K
R
2
прдx
2
2
max
, (3.77)
то станет ясно, что целесообразность использования α
х
большего 8 уменьшает-
ся, так как дальнейшее уменьшение Д
х
мало сказывается на увеличении
2
max
R
.
При
8
0x
≥α
потери энергетического потенциала 1-M[G
2
] составляют не более
11 %.
66
Все изложенное нетрудно распространить на реальные радиолинии, где
угловые флуктуации ДН антенн происходят независимо по двум углам на двух
концах радиолинии. В этом случае среднее значение
2
max
R
зависит от
( )
[ ]
∏
=
θ∆
4
1i
ii
GM
для односторонней радиолинии и среднее значение
2
max
R
зависит
от
( )
[ ]
∏
=
θ∆
8
1i
ii
GM
для радиолиний с ретранслированным активным ответом.
Если антенна используется, кроме того, для пеленгации цели в амплитуд-
ном или моноимпульсном методе, то Д
х
и α
х
выбираются из условия обеспече-
ния необходимой точности измерения угла
2
x
−
δθ
, т.е. из условий
( )
2
xx
Д δθ
и
( )
2
xx
δθθ∆
. Однако и при этом возможен случай соизмеримости Д
х
и ∆θ
х
, отку-
да вытекает необходимость учитывать потери энергетического потенциала.
При формализации задачи оптимизации радиотехнических систем рас-
смотренный эффект будет учтен в дисперсии Д
х
ошибки углового сопровожде-
ния. ∆θ
х
будет учтена в КНД антенны.
3.4. Влияние неопределенности в знании частоты на качество
корреляционной обработки сигнала, фазоманипулированного по закону
псевдослучайной последовательности
Чтобы исключить эффекты, связанные в реальным интегрированием, рас-
смотрим корреляционную обработку сигнала с идеальным интегратором.
Запишем излучаемый сигнал в виде
( ) ( ) ( )
[ ]
∑
=
∋τ
ϕ+ω+πτ−λ=
∋
N
i
i
ttacositStS
1
00
. (3.78)
Опорный сигнал имеет аналогичный вид.
Предположим, что тактовая частота независима от несущей.
Принимаемый сигнал имеет вид
( ) ( ) ( )
[ ]
∑ ∑
= =
∋τ
−ϕ+−ω+π
τ−λ=−
∋
N
i
i
i
k
i
tttacostSttS
i
1
33
1
03
, (3.79)
где
i∋
τ
зависит от движения цели, нестабильности частоты генератора такто-
вых импульсов (ГТИ) приемника относительно опорного ГТИ, t
3
- от дальности.
Механизм воздействия эффекта Допплера состоит в том, что длительность
всех элементов соответственно меняется (рис. 3.7) и поэтому одни и те же эле-
менты сдвигаются относительно опорных тем больше, чем ближе к концу пе-
риода.

67
Рис. 3.7
Из рис. 3.7 следует, что, если объект движется с постоянной радиальной
скоростью, при которой последовательность укорачивается по сравнению с ис-
ходной на величину длительности элемента, теряется половина анергии сигнала
(незаштрихованная часть).
Рассмотрим эффект подробнее.
Предположим, что имеется связь с объектом,
0
3
=δt
и свертка (выходной
эффект) ухудшается только за счет эффекта Допплера. Пусть системе фазовой
автоподстройки частоты (ФАПЧ) имеет полосу
T
фапч
1
≈Π
и допустим, что ге-
теродин за время Т не успевает перестроиться за изменениями
( )
tω∆
.
Тогда выходной эффект равен
( )
[ ]
( )
( )
[ ]
∑
∫∫
=
τ
∑
τ
τ
τ−
ω−ω−ω−ω≈Ζ
∋
=
∋
∋
∋
N
i
ii
i
вых
i
k
k
dttcosdttcos
1
0
1
0
1
2
1
2
1
(3.80)
при
∋
=
∋∋
τ<τ−τ
∑
i
k
k
i
1
; (3.81)
где
( )
[ ]
1
2
1
1
0
≈ω−ω
∫
∋
=
τ
∑
i
k
dttcos
(3.82)
при
∋
=
∋∋
τ>τ−τ
∑
i
k
k
i
1
. (3.83)
Кроме того, предположим, что
( )
t
∂
ω
практически не меняется в течение
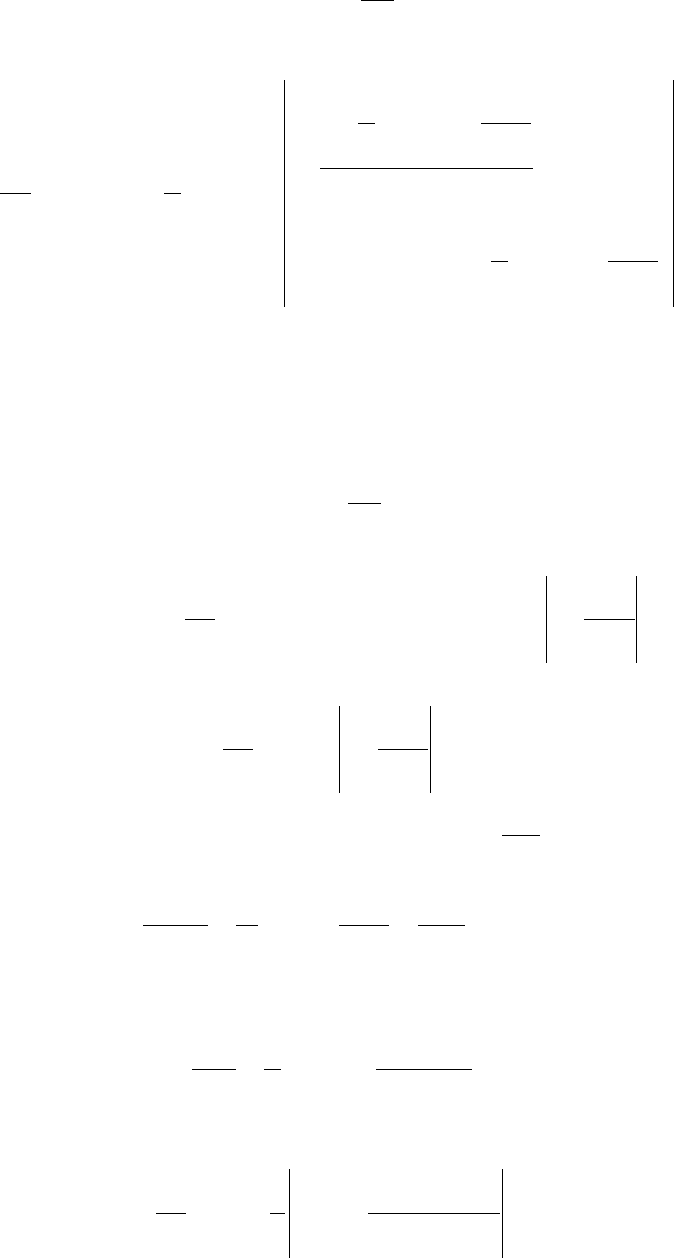
68
длительности элемента и условие (3.83) не выполняется ввиду малости
( )
t
∂
ω
:
( ) ( )
[ ]
πΠ=
π
≤ω−ω
∂∂
2
2
0
фапч
T
T . (3.84)
Тогда (3.80) можно определить как
ω
ω
τω−τω×
×
ω
ω
ω
τω
−τω
−
τ
≈
∑
∑
∑
∑
=
=
∂
∋∂∋∂
∂
=
∂
∋∂
=
∋∂
∋
N
i
i
k
k
i
i
i
k
k
i
N
i
iвых
icos
sin
icosZ
1
1
0
1
0
1
2
1
2
1
2
1
2
, (3.85)
где
( ) ( )
03
ω−τω=τω≈ω
∂∂
ii
i
.
Учитывая (3,84) в виде
N
π
≤τω∆
∋∂
2
, (3.86)
(3.85) можно вычислить следующим образом:
ω
ω
τω−τω
τ
≈
∑
∑∑
= =
∂
∋∂
=
∋∂
∋
N
i
i
k
k
i
N
i
iвых
icosicosZ
1 1
0
1
2
;
или
∑ ∑
=
∋∂
=
∂∋
τω
ω
ω
−
τ
=Ζ
N
i
i
k
k
вых
icos
1 1
0
1
2
; (3.87)
При условии (3.84), когда
Ti ≤τ≤
∋
0
, величину
0
ω
ω
∂
можно записать как
( )
( )
+++=
ω
ω
∂
!
tR
!
t
R
R
C
t
21
1
2
0
0
. (3.88)
Поскольку можно дискретизировать
∋
τ= it
, то
( )
( )
( )
∑
∞
=
−
∋∂
−
τ
=
ω
ω
1
1
0
12
1
k
k
k
i
!k
i
R
, (3.89)
где
( )
KR
k
- производная дальности R. Тогда (3.87) можно записать в виде
( )
∑ ∑ ∑
=
∋∂
=
∞
=
−
∋∋
τω
τ
−
τ
=Ζ
N
i
i
i
k k
kkk
вых
icos
!k
iR
c
1 1 1
1
1
1
2
. (3.90)
Отсюда
69
( )
∑ ∑
=
∋∂
∞
=
−
∋∋
τω
τ
−
τ
≈Ζ
N
i
i
k
kkk
вых
icos
!k
iR
c
1 1
1
1
1
2
. (3.91)
Здесь
∋∂
τω
i
icos
можно представить в виде
( )
( )
( )
2
1
1
2
2
0
222
1
2
1
2
1
−
τωτ
−=
τω
−≈τω
∑
∞
=
−
∋∋
∋
∂
∋∂
k
kk
k
i
i
!k
i
R
C
i
icos
. (3.92)
Тогда (3.93) будет выглядеть следующим образом:
( )
( )
( )
∑ ∑∑
=
∞
=
−
∋∋
∞
=
−
∋∋
−
τ
ωτ
−
τ
−
τ
≈
N
1i
2
1k
k1kk
2
0
1k
k1kk
вых
!1K
iR
C2
1
!K
iR
C
1
1
2
Z
. (3.93)
Из (3.93) следует, что если даже число периодов несущей частоты
∋
τω
0
в
одном элементе псевдослучайной последовательности велико, но меньше 10
5
,
то все равно третье слагаемое мало, так как
1
C
r
<<
υ
и
4
8
4
r
10
103
10
C
max
−
≈
⋅
≈
υ
.
Поэтому для случая, когда
3
103⋅<τω
∋∂
(3.94)
( )
∑ ∑
=
∞
=
−
∋∋
τ
−
τ
≈
N
1i 1k
k1kk
вых
!K
iR
C
1
1
2
Z
(3.95)
Если (3.94) не выполняется, то не справедливо (3.92) и необходимо поль-
зоваться формулой (3.91).
Из (3.94) следует, что по существу потерями в ФАПЧ за счет разности фаз
можно пренебречь по сравнению с эффектом изменения длительности элемен-
тов.
Из (3.95) легко определить Z
вых
непосредственно:
( )
( )
+
τ
−
τ
=
+
⋅
τ
−
τ
≈
∑∑
∞
=
−
∋
∞
=
+
−
∋∋
1k
k1kk
1k
1k
1kk
вых
)!1K(
NR
C
1
1
2
N
1K
N
!K
R
C
1
N
2
Z
(3.96)
Поскольку при
2
N
ZZ0
0вых
∋
∂
τ
===ω
, то (3.96) имеет вид
( )
( )
∑
∞
=
−
∋
+
τ
=
−=α
1k
k1kk
0
вых
!1k
NR
C
1
Z
Z
1
и
( )
( )
∑
∞
=
−
∋
=α−
+
τ
1k
0
k
1kk
0N
!1kC
R
(3.97)

70
где
1<α
∂
- коэффициент, характеризующий относительные потери за счет
данного эффекта.
Например, задаваясь потерями, для случая произвольного движения можно
определить положительный корень алгебраического уравнения (3.97) соответ-
ствующей степени, т.е.
max
NN =
, при котором имеют место потери
∂
α
.
Если произвести усечение ряда (3.97) до
й
производной, то построив
график получившейся функции
F
при
2,1=
и т.д. (рис.3.8), легко увидеть,
что
F
- монотонная и выпуклая функция для любого l.
Рис. 3.8
Поэтому для любого l хорошую сходимость к положительному корню мо-
жет дать метод касательных.
Тогда итерационное выражение для корня
n
N
уравнения порядка l и n
приближения можно записать в виде
( ) ( )
( )
( )
( )
( )
∑
∑
=
−−
∋
=
−
∋
+
τ
α−
+
τ
−=
−
−
−
1k
1k1kk
1k
k1kk
!1kC
NR
!1k
C
NR
NN
1n
1n
1nn
. (3.98)
Из рис. 3.8 и на выражения (3.98) видно, что при уменьшении значения
( )
k
R
с увеличением k и при уменьшении l сходимость (3.98) к
N
улучшается и
практически можно ограничиться первыми приближениями (n=1, 2), принимая
за
R
C2
NN
1
0
α
==
. (3.99)
Для практически интересного случая, когда
( )
1k1kk)k(
RR
−−
τ<τ
,
( ) ( )
( )
( )
( )
( )
( )
( )
∑
∏
∑
−
=
=
∋
−
=
−
−
−
∋
−
+−τ−
+
τ
α
+
−≈
1
1k
k
1i
kk
1k
1k
1n
1kk
1nn
2iR
R
1
!1kC
kNR
1
1NN
