Алексеев Г.В. Классические методы математической физики. Часть 2
Подождите немного. Документ загружается.


u
x
t
ˆu(λ, t) =
1
√
2π
Z
∞
−∞
u(ξ, t)e
iλξ
dξ.
u
ˆu u x
ξ
1
√
2π
e
iλξ
(−∞, ∞)
1
√
2π
Z
∞
−∞
∂u(ξ, t)
∂t
e
iλξ
dξ =
a
2
√
2π
Z
∞
−∞
∂
2
u(ξ, t)
∂ξ
2
e
iλξ
dξ +
ˆ
f(λ, t),
ˆ
f
f x
ˆ
f(λ, t) =
1
√
2π
Z
∞
−∞
f(ξ, t)e
iλξ
dξ.
1
√
2π
Z
∞
−∞
∂u(ξ, t)
∂t
e
iλξ
dξ =
d
dt
1
√
2π
Z
∞
−∞
u(ξ, t)e
iλξ
dξ
=
dˆu(λ, t)
dt
.
I ≡
a
2
√
2π
Z
∞
−∞
∂
2
u(ξ, t)
∂ξ
2
e
iλξ
dξ =
a
2
√
2π
∂u(ξ, t)
∂ξ
e
iλξ
∞
−∞
−
a
2
iλ
√
2π
Z
∞
−∞
∂u(ξ, t)
∂ξ
e
iλξ
dξ.
I = −
a
2
iλ
√
2π
u(ξ, t)e
iλξ
∞
−∞
+
a
2
(iλ)
2
√
2π
Z
∞
−∞
u(ξ, t)e
iλξ
dξ = −a
2
λ
2
ˆu(λ, t).
dˆu(λ, t)
dt
+ a
2
λ
2
ˆu(λ, t) =
ˆ
f(λ, t).

t = 0
ˆu(λ, 0) = 0.
ˆu(λ, t) =
Z
t
0
ˆ
f(λ, τ)e
−λ
2
a
2
(t−τ)
dτ.
ˆu u
u ˆu
u(x, t) =
1
√
2π
Z
∞
−∞
ˆu(λ, t)e
−iλx
dλ.
ˆu(λ, t)
u(x, t) =
1
√
2π
Z
∞
−∞
e
−iλx
dλ
Z
t
0
ˆ
f(λ, τ)e
−λ
2
a
2
(t−τ)
dτ.
ˆ
f
u(x, t) =
1
2π
Z
t
0
Z
∞
−∞
f(ξ, τ)dξdτ
Z
∞
−∞
e
−λ
2
a
2
(t−τ)
e
iλ(ξ−x)
dλ.
λ
Z
∞
−∞
e
−λ
2
a
2
(t−τ)
e
iλ(ξ−x)
dλ =
Z
∞
−∞
e
−λ
2
a
2
(t−τ)
[cosλ(ξ − x) + isinλ(ξ − x)]dλ =
= 2
Z
∞
0
e
−λ
2
a
2
(t−τ)
cosλ(ξ − x)dλ =
√
π
2a
√
t − τ
e
−
(ξ−x)
2
4a
2
(t−τ )
.
u
u(x, t) =
Z
t
0
Z
∞
−∞
1
2a
p
π(t − τ)
e
−
(ξ−x)
2
4a
2
(t−τ )
f(ξ, τ)dξdτ.
f
f ∈ C
1
(Q
T
), lim
x→±∞
f(x, t) = 0, lim
x→±∞
∂f(x, t)
∂x
= 0 ∀t ≥ 0.

ˆ
f
c
(λ) =
r
2
π
Z
∞
0
f(ξ)cosλξdξ,
ˆ
f
s
(λ) =
r
2
π
Z
∞
0
f(ξ)sinλξdξ, 0 < λ < ∞
f(λ) =
Z
∞
0
f(ξ)e
−λξ
dξ, λ = σ + iτ, 0 < σ
0
≤ σ.
u
x
ϕ
α < x < β
u(x, t) =
Z
β
α
ϕ(ξ)
1
2a
√
πt
e
−
(ξ−x)
2
4a
2
t
dξ.
t > 0
x u(x, t)
t > 0
x t
ϕ
(x
0
− h, x
0
+ h) x
0
ϕ
(x
0
− h, x
0
+ h) ϕ
0
Q = 2hρcϕ
0
ϕ
0
ρ c
u(x, t) =
Z
x
0
+h
x
0
−h
ϕ
0
1
2a
√
πt
e
−
(ξ−x)
2
4a
2
t
dξ =
Q
2aρc
√
πt
1
2h
Z
x
0
+h
x
0
−h
e
−
(ξ−x)
2
4a
2
t
dξ.
h
Q
x = x
0
Q
t = 0
x = x
0
lim
h→0
Q
2aρc
√
πt
1
2h
Z
x
0
+h
x
0
−h
e
−
(ξ−x)
2
4a
2
t
dξ.
1
2h
Z
x
0
+h
x
0
−h
e
−
(ξ−x)
2
4a
2
t
dξ = e
−
(ξ
0
−x)
2
4a
2
t
, ξ
0
∈ (x
0
− h, x
0
+ h).

ξ
0
→ x
0
h → 0
Q
2aρc
√
πt
e
−
(x
0
−x)
2
4a
2
t
.
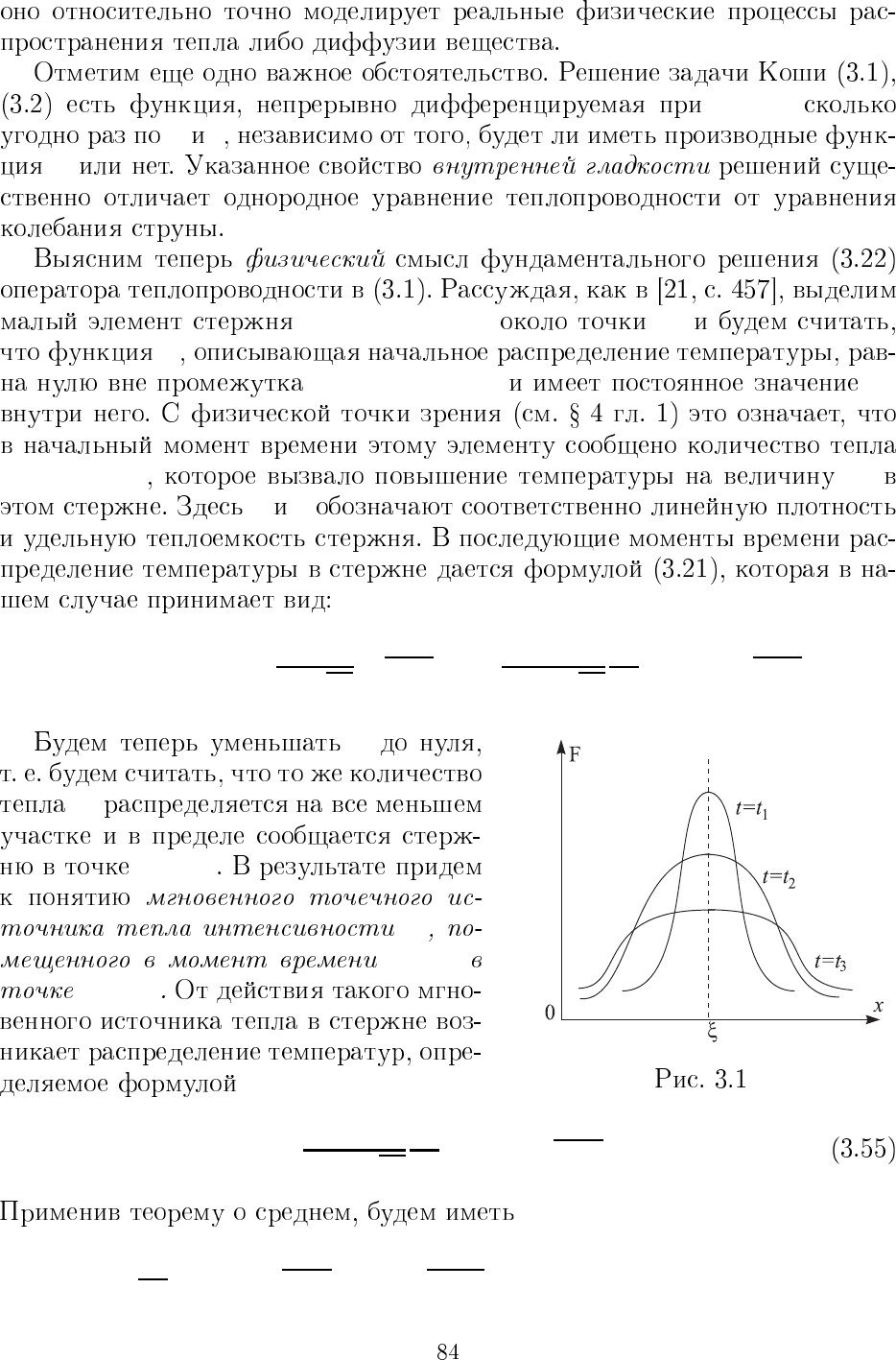
Q = ρc F (x
0
, x, t)
Q = ρc t = 0 x = ξ
F (ξ, x, t) ξ
x t
1
< t
2
< t
3
Z
∞
−∞
1
2a
√
πt
e
−
(ξ−x)
2
4a
2
t
dξ =
1
√
π
Z
∞
−∞
e
−α
2
dα = 1 .
Q = ρc
(ξ −ε, ξ +ε)
ε t > 0
ρc
t = 0
t > 0
x = ξ t = 0
x = ξ

∆u = 0
∆ § 3
∆u = −f,
∆
Ω
f
f
∆u = 0,
Ω
R
n
n ≥ 2
n = 3 n = 2
Ω
e
= R
n
\ Ω
u : Ω → R
Ω Ω
x ∈ Ω
u : Ω
e
→ R
Ω
e
Ω
Ω
e
Ω
e

x ∈ Ω
e
|u(x)| ≤
C
|x|
n−2
.
u
x
Ω
u
Ω
Q ⊃ Ω
Γ Ω
R
3
R
2
R
3
x y z r, θ ϕ ρ ϕ, z
x ∈ R
3
∆
∆u =
∂
2
u
∂x
2
+
∂
2
u
∂y
2
+
∂
2
u
∂z
2
∆u = ∆
r,θ,ϕ
u ≡
1
r
2
∂
∂r
r
2
∂u
∂r
+
1
r
2
sinθ
∂
∂θ
sinθ
∂u
∂θ
+
1
r
2
sin
2
θ
∂
2
u
∂ϕ
2
∆u = ∆
ρ,ϕ,z
u ≡
1
ρ
∂
∂ρ
ρ
∂u
∂ρ
+
1
ρ
2
∂
2
u
∂ϕ
2
+
∂
2
u
∂z
2

r ρ
r
u
θ ϕ
1
r
2
d
dr
r
2
du
dr
= 0, r = |x| > 0.
r
2
u(x) = U(r) ≡ C
1
/r + C
2
C
1
C
2
C
1
= 1/4π C
2
= 0
u(x) =
1
4π|x|
≡
1
4πr
.
R
3
x = 0
x 6= 0
|x|
−1
R
3
\{0}
R
3
1/|x| 1/4π
r
x = (x
1
, x
2
, x
3
)
y = (y
1
, y
2
, y
3
) ∈ R
3
E
3
(·, y) : R
3
→ R
E
3
(x, y) ≡
1
4π|x − y|
=
1
4π
p
(x
1
− y
1
)
2
+ (x
2
− y
2
)
2
+ (x
3
− y
3
)
2
, x 6= y,
Ω R
3
y
y = 0 y 6= 0
y

R
3
y
R
3
ρ
u(x) = U(ρ) = C
1
ln
1
ρ
+ C
2
.
ρ x y
ρ =
p
x
2
+ y
2
.
z z = 0 R
2
C
1
= 1/2π C
2
= 0
u(x) =
1
2π
ln
1
ρ
=
1
2π
ln
1
|x|
, ρ = |x| =
p
x
2
+ y
2
,
R
2
E
2
(·, y) : R
2
→ R
E
2
(x, y) ≡
1
2π
ln
1
|x − y|
=
1
4π
ln
1
(x
1
− y
1
)
2
+ (x
2
− y
2
)
2
, x 6= y = (y
1
, y
2
),
R
2
y ∈ R
2
R
2
y = 0
∆u ≡
∂
2
u
∂x
2
+
∂
2
u
∂y
2
= 0
x 6= y
|x| → ∞
R
2
y
R
2
x = y
Ω ⊂ R
2
y
R
n
n ≥ 3
ω
n
R
n

ω
n
= 2π
n/2
/Γ(n/2) Γ
E
n
(·, y) : R
n
→ R
E
n
(x, y) ≡
1
ω
n
|x − y|
n−2
, x 6= y, n ≥ 3,
|x − y| =
p
(x
1
− y
1
)
2
+ (x
2
− y
2
)
2
+ ... + (x
n
− y
n
)
2
x = (x
1
, x
2
, ..., x
n
)
y = (y
1
, y
2
, ..., y
n
)
Ω R
n
y
R
n
y R
n
y = 0
E
n
(·, y) n = 3
q
y ∈ R
3
(y, q)
y q
u
(y, q) x R
3
u(x) =
q
4π|x − y|
≡ qE
3
(x, y).
E
3
(x, y )
x ∈ R
3
y
u
E(x, y) = −kq∇
x
E
3
(x, y) x
∇ E
3
x k
k = 1 E(x, y)
x ∈ R
3
(y, q)
x
r = |x − y| =
p
(x
1
− y
1
)
2
+ (x
2
− y
2
)
2
+ (x
3
− y
3
)
2
∂r
∂x
i
=
x
i
− y
i
r
,
∂
∂x
i
1
|x − y|
≡
∂
∂x
i
1
r
= −
1
r
2
∂r
∂x
i
= −
x
i
− y
i
r
3
,
∂
∂y
i
(
1
|x − y|
) =
x
i
− y
i
r
3
, ∇
x
1
|x − y|
= −
x − y
|x − y|
3
= −∇
y
1
|x − y|
.
