Алексеев Г.В. Классические методы математической физики. Часть 2
Подождите немного. Документ загружается.


E(x, y) = −kq∇
x
1
4π|x − y|
=
qk
4π
(x − y)
|x − y|
3
.
y q
x ∈ R
3
(y, q)
E
2
(·, y)
R
2
R
3
E
2
(x, y)
x ∈ R
2
y ∈ R
2
E
2
(x, y)
x ∈ R
3
x
1
= y
1
x
2
= y
2
x
3
y
′
= (y
1
, y
2
) ∈ R
2
E
3
(·, y)
y
e
1
l
1
y
′
y
′′
l
1
y h
−q q
q > 0
(y
′
, −q)
(y
′′
, q) x 6= y
′
, y
′′
u(x; y
′
, y
′′
) =
q
4π|y
′′
− x|
−
q
4π|y
′
− x|
.
h = |y
′
−y
′′
| → 0 u(x; y
′
, y
′′
)
h → 0
h q
qh = q|y
′
−y
′′
| = q
1
q
1
(y
′
, −q) (y
′′
, q) h → 0
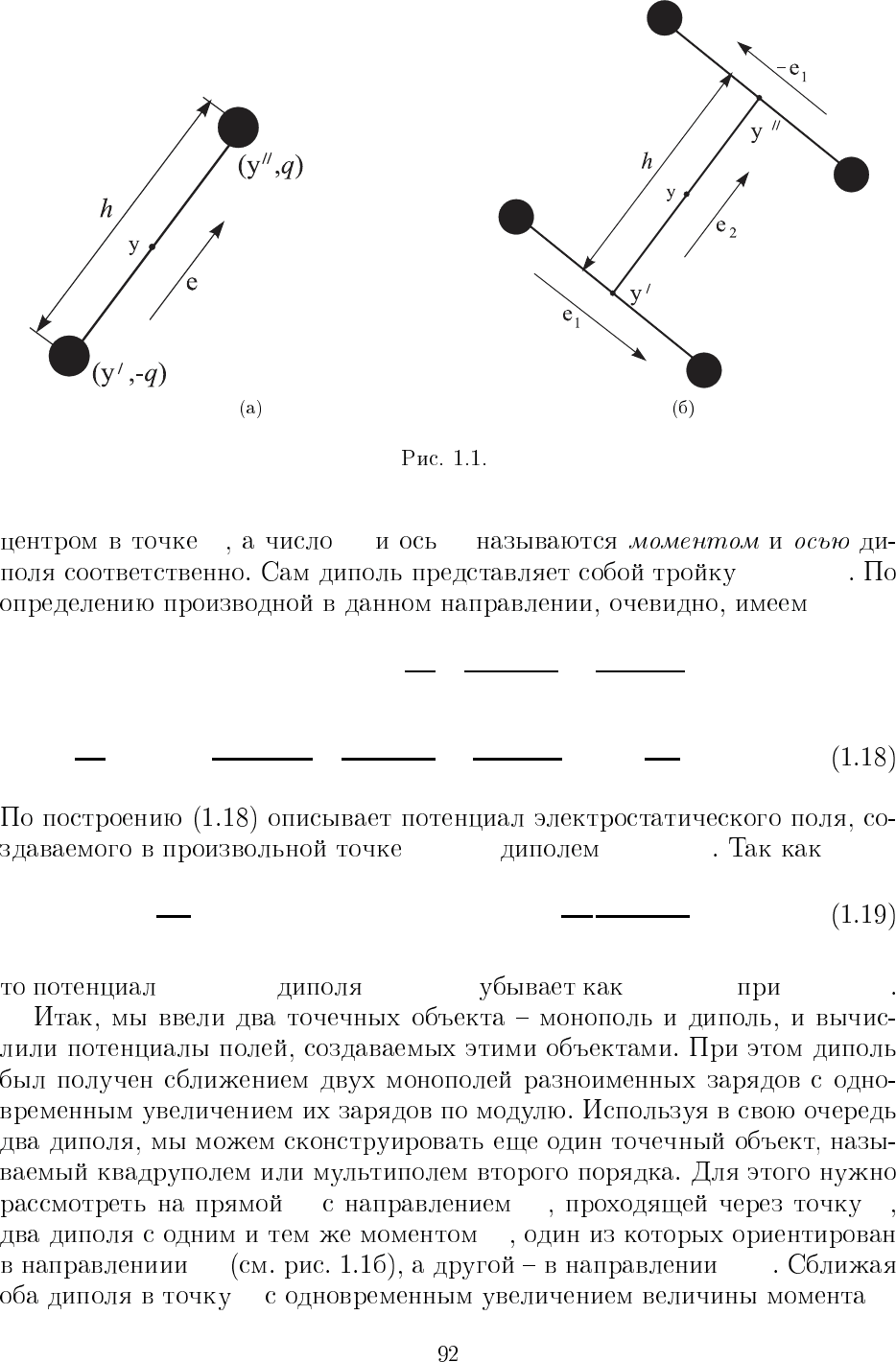
y q
1
l
1
(y, q
1
, l
1
)
u
(1)
(x, y) ≡ lim
|y
′′
−y
′
|→0
q
4π
1
|y
′′
− x|
−
1
|y
′
− x|
=
=
q
1
4π
lim
|y
′′
−y
′
|→0
1
|y
′
− y
′′
|
1
|y
′′
− x|
−
1
|y
′
− x|
= q
1
∂
∂l
1
E
3
(x, y).
x ∈ R
3
(y, q
1
, l
1
)
∂
∂l
1
E
3
(x, y) = ∇
x
E
3
(x, y) · e
1
= −
1
4π
x − y
|x − y|
3
· e
1
,
u
(1)
(x, y) (y, q
1
, l
1
) O(|x|
−2
) |x| → ∞
l
2
e
2
y
q
1
e
1
−e
1
y q
1

2!q
1
h ≡ q
2
= co nst
u
(2)
(x, y) =
q
2
2!
∂
2
∂l
1
∂l
2
E
3
(x, y).
q
2
l
1
l
2
O(|x|
−3
) |x| → ∞
y
u
(3)
(x, y) =
q
3
3!
∂
3
∂l
1
∂l
2
∂l
3
E
3
(x, y),
O(|x|
−4
) |x| → ∞
k u
(k)
(x, y)
u
(k)
(x, y) =
q
k
k!
∂
k
∂l
1
∂l
2
...∂l
k
E
3
(x, y).
l
i
q
k
k
k
E
3
(·, y)
O(|x|
−k−1
) |x| → ∞
E
n
(·, y)
y
R
n
R
n
\{y} E
n
(·, y)
x x → y E
n
(x, y)
n
n ≥ 3 E
n
(·, y)
R
n
\{y}
n = 3 E
n
(·, y)
x ∈ R
n
y ∈ R
n

E
n
r = |x−y|
r = |x − y|
E
n
E
n
R
n
× R
n
→ R
x y E
n
(x, ·) y
x
E
n
(·, y)
E
n
(·, y)
∆
x
E
n
(x, y) = −δ(x, y).
x ∆ E
n
x δ(·, y) n δ
y ∈ Ω δ
δ(x, y)
y
R
∞
−∞
δ(x, y)dx
δ(x, y)
δ(x, y)
δ
D(R
n
) R
n
< δ(x, y), ϕ >= ϕ(y) ∀ϕ ∈ D( R
n
) < ·, ϕ >
ϕ ∈ D(R
n
)
E
n
(·, y)
E
n
(·, y)
Z
R
n
E
n
(x, y)∆ϕ(x) dx = −ϕ(y) ∀ϕ ∈ D(R
n
).

N (y
1
, q
1
) (y
2
, q
2
)
(y
N
, q
N
) y
1
, y
2
, ..., y
N
u(x) ≡ u(x; y
1
, y
2
, ..., y
N
) =
N
X
j= 1
q
j
E
3
(x, y
j
) =
N
X
j= 1
q
j
4π|x − y
j
|
.
Ω ⊂ R
3
ρ : Ω → R (Ω, ρ)
(Ω, ρ)
Ω N
Ω
j
Ω
j
Ω
j
→ 0 N → ∞
(Ω, ρ)
u(x) = U[Ω, ρ](x) =
Z
Ω
ρ(y)dy
4π|x − y|
.
dy Ω
x
x /∈ Ω x ∈ Ω
y → x ∈ Ω
ρ
Ω (Ω, ρ)
(Ω, ρ) ρ
Ω (Ω, ρ)
(Ω, ρ)
(Ω, ρ)

Γ ρ : Γ → R
(Γ, ρ)
u(x) = U[Γ, ρ](x) =
Z
Γ
ρ(y)dσ
y
4π|x − y|
,
dσ
y
Γ y ∈ Γ
x /∈ Γ
x ∈ Γ
ρ Γ
(Γ, ρ) ρ
Γ
ρ Γ
(Γ, ρ)
Γ
n
y
y
y
l
Γ
q = ρ(y)
y ∈ Γ l
n
y
Γ y
(Γ, ρ, n)
u
(Γ, ρ, n)
u(x) = U[Γ, ρ, n]( x) =
1
4π
Z
Γ
ρ(y)
∂
∂n
y
1
|x − y|
dσ
y
.
Γ ρ
Γ
Γ
h
h

n
Z
Ω
E
n
(x, y )ρ(y)dy,
Z
Γ
E
n
(x, y )ρ(y)dσ
y
,
Z
Γ
∂
∂n
y
E
n
(x, y)ρ(y)dσ
y
, x ∈ R
n
.
n ≥ 3
n = 2
1
2π
Z
Ω
ln
1
|x − y|
ρ(y)dy,
1
2π
Z
Γ
ln
1
|x − y|
ρ(y)dσ
y
,
1
2π
Z
Γ
∂
∂n
y
ln
1
|x − y|
ρ(y)dσ
y
,
x
Ω ⊂ R
3
f
x
0
∈ Ω
ω
δ
x
0
f
Ω\ω
δ
ω
δ
x
0
∈ Ω x
0
∈ ∂Ω

δ ω
δ
x
0
δ → 0
Ω ω
δ
f
Ω
Z
Ω
f(x)dx = li m
δ→0
Z
Ω\ω
δ
f(x)dx.
ω
δ
x
0
R
Ω
fdx
ω
δ
n
I = lim
n→∞
Z
Ω\ω
δ
n
f(x)dx,
I
I ω
δ
n
f x
0
∈ Ω
Z
Ω
f(x)dx = lim
n→∞
Z
Ω\B
δ
n
(x
0
)
f(x)dx.

B
δ
n
(x
0
) δ
n
→ 0
x
0
x
0
∈ Ω
R
Ω
f(x)dx
B
δ
n
x
0
δ
n
→ 0
f Ω
n
Ω Q R
3
F
Q × Ω
J(x) =
Z
Ω
F (x, y)dy, x ∈ Q.
x ∈ Q
x
Q Ω R
3
F Q ×Ω x y
J Q
∂F
∂x
i
Q ×Ω J
x
i
Q
∂J(x)
∂x
i
≡
∂
∂x
i
Z
Ω
F (x, y)dy =
Z
Ω
∂F (x, y)
∂x
i
dy , x ∈
Q, i = 1, 2, 3.
J
x
Z
Q
J(x)dx =
Z
Q
dx
Z
Ω
F (x, y)dy =
Z
Ω
dy
Z
Q
F (x, y)dx.
J(x) =
Z
Ω
F (x, y)ρ(y)dy.

F
ρ
R
Ω
|ρ(y)|dy = I = const < ∞
R
Ω
|ρ(y)|dy
F Q × Ω
x
i
i = 1, 2, ..., n m ≤ ∞ J ∈ C
m
(Q)
J
(Ω, ρ) ρ
Ω x Q
Ω F
x ∈ Q y ∈ Ω
F (x, y) =
1
4π
1
|x − y|
,
(x, y) ∈
Q × Ω u
x
i
x ∈ Q u x
i
x
i
∂u(x)
∂x
i
=
1
4π
Z
Ω
∂
∂x
i
1
|x − y|
ρ(y)dy = −
1
4π
Z
Ω
x
i
− y
i
|x − y|
3
ρ(y)dy, i = 1, 2, 3.
x Ω
y = x
x ∈ Ω
ρ
x
i
x ∈ Ω
x ∈ Ω
Ω R
3
ρ Ω |ρ(y)| ≤ M ∀y ∈ Ω
F x ∈ Ω y ∈ Ω x 6= y
y → x ∈ Ω
