Агошков В.И. Задачи и уравнения теории переноса частиц
Подождите немного. Документ загружается.


(2.6)
(2.7)
:.
-20-
~!
J
rtr'J
<lJL'
'f'(r.jt'.E:i)'(~(r.E:r=.",)I,iJ+L.(r,f;EJ
t)
:De
-!
с.
-t
-JL
l (r,
Е:
Е,
i
))+-t,
(r.E,t ) +
.f
~
(r,
'!
Е,
i
);
'f(R,р,Е;f:)=Ч'r(}l)f,i)
при
-j~)i<o;
Ч'(t',J',Е,оJ=
tf.
(f')JW,
E)
,
(2.8)
rne
2Х
...
L:
s
(,.,
Е
,'Е
,)IA"l',i)=гi
J
d-1fL;$
(r,t:E,}'p'.J1-
}l&J1-)l'~COS("'-'I'
~
-t)=
.
()о
О.
.
(м)
1.
I
J..
27
·t L:s,t
(",Е;
i
~
(2т+1)'\.Х{,е
tЕ,~)z.зr
J
obp,F;.r,-,~J4-уJt"1''\.оs{Ч'-'f~1
Внрааение
,'UJUI
ФJвкцви
инте1",l8JlЫlОro
потока
здеоь
имеет
вц
4
1f(",E,i)=2.:J1
tf(r,~IE.t)clj.t.
(2.9)
-.
Замечание.
ЛвиyJ)
чаоть
уравнения
(2.6)
часто
удоdио
предетaв.mrrь
в
дивеРГeJmlоl
фоJll8:
.
2.
•
i.~
...
.L:L(rlJVIf)+~
(~fI)+L:
If
(2.IO)
IГ
Я
rl.
~,..,
dJl"
t ·
:·В.-
Ц
и
JI • R
ДР.
ч
ее
х и
-
с
и
м м
е
т
р
и
ч
и а
11
r
е
ом
вт·р.
11.
ПреДПOJIODII,
что.:D
встъ
ЦIIJ.DЩЦp
!ВООТН
Н
И
Ра,циуса
OOВOвaвJDI
:R
,осъ(
о.
l
)..
осъ
Ц1IJIИВДpIIЧ80хоl
ОDRетрп
и
все
фymщии
(коa)l)ицвевтн,
иоточники,
решение
и
т.д.)
1
а,
""&
--_.-
.
зависят
от
.r
посредотвом
r:::
( %4 +
Xt)
и
1==
Х
З
(рис.
2).
___
X,-.:l
1rловую
зависимость
их
будем
ВН-
puшть
..
через·
yrJIы
е
и
'"
,
где
е
-
yrOJl
Mez.uy
иaпpaвJIеиием
поле
та
нейтрона
и
БеpтивaJIЬJ)
В
точке
(
2:4
t Xl. t
Х)
) "
ч'
-
yro11.
между
прое1ЩИеlнапpaвJIеиия·поле'l'S
нейт
рона
на
ПJIОСROСТЬ
(
~4
,
%1
)
И
%'1
(
О
~
е,
3с
,0
~
ЧJ'
zЖ'
).
Tor-
да
в
переменвнх
(
~
f
~
,jJ*c.ose
t
'V
,
Е
t t )
задача
(I •I t
),
(1.2),
(1,3)
имеет
вид
..
dЧ'
.
d«f
{--;-:т.(
.
Э<f
_ Sin. W
~
) +
1'_
u:
я-
+
jU
~
+.Ji-JU-c.c5tf~
--;:;-
dtp
~itp
- .
2~
~
::
4~
J
t1E'J
d.t/J
I J
df'
<f
(")~.i
,'1",
Е,
{).
:D
E
О
-1
.(~(r-i
Е'
Е
IIL.,{.)+~.
C,.,i,E',E,-t)+
~$
),
)
~),..
...
L..

- 21 -
40~~!
(",
(,
Е
'.
E;I:»)
+
{('"
хо,
E,-t)+
~
(r,
i.
'!'
1/',
E,i);
4'(R,~.}L,Ч',
E.t)=
Ч'r(:l,f,(jI,f,i),
f <
qJ~
.3{
,
Ч'(r.
Н"'Ч',
EJ)=-
tf
r
Сr."Ч'.Е.1),
-1'
Je
<
о
, .
ер
(r,o,}t)
11',
Е,
t.)
=
fr(r.jI(,
'1'.
Е,
t.),
0<
Jl
~
i ;
(2.1I)
~
(2.12)
) .
t('(r,i,}',tfI,E,O)
::
Ч'о
(r,~)},qJ)E),
(2.13)
где
}lо
=
J"
1+
Ji-Jl'-
.J
1-
jU'1.
Ct>S
('"
-
",')
•
Фyшщ1UI
ИВ'l'еrp8JIЬВОro
пото:ка
здеоь
имеет
вид
~
2Ж
\f(r,7l,
E.-t
):
j
CL,
J4
!f
("il,jt,
Ч',
Е,
i).
(2.I4)
-1
.
О
§
з.
I'paвичнIIе
УОJIOВИЯ
06JIaсть1'
Может
6нтъ
образована
pI.ЦOM
зои
С
разJDIЧВШIИ
000"'.
тавами
•.
При
переоечеиии
rpaвиц
раз.цепа
этих
зов
фYВJa1JUI
потока
ие:l'r
ронов
доmшa
быть·
вепрернвноl.
Точнее,
в
таких
СJI1Ч2SiX
необхо-
димо
требовать
непрерывность
от
,.
tp
(.!+
JQ
,Q t
Е
t
-t.
+ r/
lr
(
Е.
»
:как
фymщии
от
~
•
где
~
-
расстояние
вдoJlЬ
ваправ-
J1ения
Q •
При
В1ШОJПIевии
Э'l'Оro
УОJIОВИЯ
уравнение
переноса
запи
сывается
в
фо];N8
(I.I')
по
обе
оторовк
от
поВерхности
р1Зде.па
(а
на
самой
поверхнооти
ДОD80.иметь
место
отмечеШlое
УОJlовие
веп
рернвности
tf
).
Имеиво
в
тalCOM
ОМНОХ8
И
повимается
запись
(1.1')
t
хотя
ранее
мы·
спеnиaльвои
не
вuдеJJЯJIИ
с.пyчal.
мвоroэовиоl
оdJIaети.
-
Отмеченное
выше
условие
вепрернвнос'l'И
<f
(!
+sQ
_~
•
Е.
t + 5/
tr
)
и
преДОТaвJIЯ:ет
..
ообоЙ
1'1ВВJIЧВ08
УОJ!овие
д.шI
tp
на
rp1ВИIJ11X
раздела
зои.
.
06ра.тШl.СЯ
теперь
к
условиям
на
rpaницe.
оБJIaсти
dD
•
Ес
ли
на:Ь
падает
извне
потох
иеЙ'1'роИОВ
ЧJ
r
,
то
на
dJ)
,1WI
ч'
записываетоя
rpa.mгmoe
УСJIOвие
(1.2).
Это
УОJIовие
я:вляетоя.част
ным
случаем
06щеroУСJlОВИЯ
mщa

(З.I)
. .
~
22
-
Ч'
(,:
,Q
>
E;t)"
J
dE'
J
dQ
'R
(1:'
.Q
',.Q
,Е:
E;i}
.
::Ь
е
Q,
~.!!»O
•
tp(!:.Q.',E',1:
)+4'r(!:,Q,E,t)
при
.t
f
dD
w (
~
.lЗ
) <
о
1
r.-e
фyиRЦIIII
R
харехтериэует
возвра.,
в
ОdJlacтъ.:D
ВЬ1JI8тa»-
-.их
из
обlaоти
нейтронов.
Звачевие
R;
о
соответотвует
СJIYЧ8Ю
t
JЮr.ца
IIЗвне
нa:D
па;цает
эа.цаиннl
поток
«р
('
,
а
ВWIетaDltИе
из
J)
веЙ'rpOИН
ие
эадерDВaJ)ТСЯ
rpaиицеl
~'!:>
•
УСJIОВИЯ
:вида
(3.I)
1JCтр8чam'CJI
в
I8ЭJDIЧННX
зaдt1чах
теории
JtЦeJВНX
реаторов:
при
рас-
че'l'8X
ячеек.
расчете
381Q11'1'W
реактора
и
т.д.
"
Рассмотрим
еще
0_
'l'JD1
УСJlОвd
-
периодические.
Пусть
т
!'J)8D18p118J1
мa'lpкq1
•
dd.
т
..
о
•
Оdoзвачим
! = (
~
i
,I<:~
,
I(~)
':вектор
о
Ц8J101IИ0Jl8JIШIМИ
компонентами.
Пуоть
таае
~
=
'"
2жt
v
,
r.цe
~
"j
ER
s
•
ПреДl1OJlODМ,
Ч'tО
все
проотраиство
эапОJПIёiiо
веществом,.
причем
в
точках
.0000JIИ1IaIIЦIIXОЯ
)@yr
ОТ
.цpyra
.
А
на
В8Х!'О1&
ВJU18
2(Ж
'f
~,
овоIО'l':&а
вещеотва одни
и
те
ае.
Поэ-
тому
О'1'ОU8СТВВМ
вое
эти
'1'очхи.
ПоцучеJШое
lIВоroО(Sр18ие
всех
экви
вuell'1'RНX
'1'очек
Dpe.ЦС'1'81UIЯ8'1'
собой
тpexмepm4.
тop:D
•
ROТOpнA
В8анваетosr
фYвдI.шеИ'r8JIЬRоl
оБJIacтью
ЩIJI
2;к
Т
-
периодических
фymt
nИЙ.
Tatt
ваэн:ваютоя
фувкции
.
-:t
(~
),
ДJJЯ
ROторнх
при
Jm60м
Х
И
JШбoм
Ц8JtOЦОJI8ВИОМ
8<Спpmв)UDlВO
равенотво
.t
(~
)=
=
f
(~
+
2«1'.!S.
).
пР;
ПОМОЩИ
разрезов
TOp:D
может
быть
прев
р!Щ9Н
В
ОДВООВИ8Ql)
оБJJaс'1'Ъ
t
например
В
It1б.
-
~
~
)/ё.
~
~/
2,
J
t =
It2,З~
~
'feперъ
пр8ДПQJIОпrь,
~~
..
~
f
e
,
<РО
JlВJUlDrCЯ
2~
I
~ериодичесXИМII
по
прос'1'равствевинм
переменинм,
то
ка
1)
можно
pacoмo-rpeтъ
8tUV1Ч1
Д1DI
)'PlВВ8ВИЯ
переиооа
(I.
I ' ) •
ТoJIЪВO
SJ(eCb
вместо
~
YCJloвdвa
О'l'Нсюtвa.емое
решение
IIaк.ла
...
днвается:
УOJIОвие
2z-T
~
периодичноо'l'И:
(3.2)
10JlО_-
(3.2)
широко
испonзуе'1'ОЯ
в
ззддчах
plсчета
ячеек
в
ядер
ном
peaRТope.
ТaR.
.
еоJ!И
пpeдIIOJIOJtИТЬ
t
ЧТО
R
з
запОJПIено
meоти
rpaНJПМI_JIЧeIRaми,
то
легко
~J1И'1'Ь
0БJIасть
периодичности
])
(рис.
З),
и
здеоь
1В'l'Pиц:\"
имеет
вид

-
23-
~.
~~2·
О
О
л
1/2, .
1=\
ol
О
О
о
1
:l1
Есди ячейки
квадратные,
то
матрица
т
-
единичная.
ОТметJШ.
что
в
не-
)~
которых
нестациоварннх
задачах
теории
ядерных
реакторов
условие
периодич-
Рис.
з.
ности
(например,
С
периодом
'т
)
вак-
мднваетоя
на
решение
эадач:и
и
по
временной
переменноl
(3.3)
с-
(вместо
условия
Капи
(I
.3)
) •
§
4.
СОI1pfDlенное
уравнение
Уравнение.
оопряжеввое
уршнеmm
перенооа
(1.1')
t
иrpaет
ва&
ную
pon
В
теории
ядерных
реактороВ
(в
теории
возмущений.
ва
риациошna:
расчетах
и
Т.Д.)."
Ero
решения,
часто иазнваемне
.шшm-
.
Ж8НННМИ Функци.ями,или
ФУнкпиями
цеШl9СТИ,
имеют
яоmdl:
физичеоКИЙ
смнсл
цеlUlОСТИ
нейтронов
в
реакторе.
"
ЕсJIИ
рассмотреть
ИСХОднyl)
задачу
Д)IЯ
уравнения
перевоса
в
ФО1Ме
(1•1' )- (1•
З)
без
учета
запазДнвапци.х
нейтронов,
то
оопps:-
аеИШUI
R
вей
задача записывается
СJl8дynцим
оdразом~
-t
;i*-
(Q,
V)
'РУ
+
L:
t
If'~'"
~
J
.Н:'
J(L
s
(!:,
Е,Е:,о,
{)
+.
:t>. Q
+
2.:.
(!:,Е
,Е:
{)
+ )lL.,
Cr:,E,E:
i)cp*(r.Q:
E',-l.J
d,Q'
+~;
(!:
,Q,E;t
);
(4.1)
f"(!:,.Q,E;t)=
ч>;
(!:.Я,Е,+)
при
("Еа])
• (.Q,g)>o;
(4.2)
\(>*(!:'
,Q,
Е
.Т):
~;
(!:..Q,
Е),
(4.3)

.. 2-' ..
r.цe
tp*
(
!:
.g
.
Е
• t ) -
фyвIщu
цевиОО'l'И.
1:5
•
~t
•
~
L.
опредеJl8НН
ранее.
(э.цео:ь
имеет
мeo'fO
замена
перемеВIIНX
4
')
р*
.. *
ф
Е
"~E
".
14
•
Ч'r
•
<Р,.
'-
.ацаввне
ркцп.
Ее.
YIIН08IIТЬ
(4.1)
на
ре_П8
JPUВ8JDD1
(1.1'),
а
yp:uJВe-
пе
(1.1')
-
на
<р
~
,~'1'811
реЗУJlЬ'1'атк
ПРОJDrr8I'}8рОDa'1'Ъ
по
оdaоп
'1=
(O;1')x.D
e
-Q.1)
•
внч:ес'1'Ь
ОАВВ"О
.цpyroro,
то
прцеll
R
ив
вео'1'ИOII1
QОО'l'ИОlеивр
оопpgeвиооп
(COOТIIOl8D1)
В88ИМRООП),
_-
ром
ВОПОJlЬЗУемому
в
раэJIIIЧIIНX
раОЧ8'l8X
•
теоретических
ИООJIедо-
В8НIUIX:
1
с
I
в
(4.4)
rJte
+ J
J.fr
«t
d2
ike>
CP(r,g,E,rr)tp;(t,Q,E).
(4.6)
~E
J>-Q
""
•.
PaccftfO'J.'l8l
одно
JIЗ
В08l&)JaIНX
примевеииl
ООО'1'иоmeиия(4
.4)
."
Пред
поло
....
,
Ч'1'О
в
(I.It,1J(I.~)
-eeм:'r
=
О.ЧJо=О
и
при
88Д8ВВOII
ИСТОЧВlПte
•
.f
c
(...
=
1,
••••
No)
требуется
найти
ооответ-
С'l'вуоцее
решение
'Ре..
•
а
затем
опре.цеJlИТЪ
ЧИОJIО
8RТOB
...
некото
poI'O
цроцесса,"
имеЩ8ro
сечение
Ed.,
(1:
,Е
"'
t )
в
объеме
о
:D
aI.
со
Ь
•
Это
ЧИС~О
МОЕет
быть
предотав.лено
функционаJIОМ
• •
'1
•
JJ
..
•
. (
I
. 4
~
•
с

•
,
I
., 25 ., .
7'
l)'Ip·»::JdiJ<kfdQJd~L;~
"т.
(4.7)
о
J)~
.Q. .
7Je
..,.
~-
о
. ,-
EOJIII
теперъ
:в
(4.1)-(4.3)
пpJUIJIТъ
ЧJ
r
::
О,
'р:::
,а
8
=-
~
'"
в
o<1IaCT.
J).c. •
1;
==
О
в
:D'.J)o(
•
то
corJla080
(4.4)
8CКOl108
_OJIО
актов
процвооа
МОаН0
представить
TaIClt8
в
фоple
" .
I~
(tp;)
=:
f
сН
f
d!]dQ
JdE
((~.Q,E,t)
'Р;
.
о
.:D
Q
З>r;
..'
.
Таким
образом,
о'1'НСкав
решение
~oe.
сопраевиоl
ЭЦ8ЧИ.
1&1
uoaем
затем
находить
ЧВOJJa
IoI.
("
(i» = 1
i.
('Р
=.
), l
...
1,
...
,
'(.
Пfтем
ВНЧIICJlеВIISI
птеrралов
(4.8).
Очевцно,
что
такой
пrrъ
поJ.l1
Ч81111J1
Tpedyeмнx
реЭУJIЪтатов
roраэ.цо
экономнее
(осodевво
при
БОА
ax.N
),
чем
птrъ
вепосредотвеввоro
рвшеВJIJI
эцач
ппа
(1.
~
,
)-
.
(1.3)
•
ВНЧIICJlеВИSI
JlRтеrра.и:ов
(4.7).
§
5.
Мвоrorpy1lПOвое
приC1lDeвие
ПоскOJIЬRy
ко8фрициевтнs
JP8Ввевп
(1.1)
IDIeИ
Becыв
саоа
RYI)
зависJDlOОТЪ
от
8верrп.
то
ивпооре.цоuеВН09
реиввив
88Д8Ч
(I.I)-(I.3)
•
(3.1)-(3.3)
в
Бo.lыlивтвеe
CJ17Ч88В
В8СЫВ
88'1'P1дIIII
ТQlЪио.
ПоэтоМу
A7IJI
решения
этих
задач,
как
пpaвuо,
8СПOJlЪЭym
метод
мвоrorрупповоro
при6JПD1еlDlJt.
Первd
8'1'8D
8t'Oro
lIpIId.laeвu
1\
состоит
В
ТОМ,
Ч'l'O
рассматрИВавмu
эвеpre!'Jl1l8OR8Jl
0С1ас1'Ъ
~
.D
f'
=(
Е
tr1tt1 ,
Е
тa~
)
(рис
•
4)
i-t
4-1

-26-
I
rруппа
G
rpуппа
2
rруппа
1
111
•
I
,
,
E
G
E
G
-
1
F2.
Е"
Е
тах
РЕЕ
~
Е
мin
Рис.
4
I
I
J
,
(5.I)
Рве.
5
раэdивается
на
:конечное
ЧИCJIо
Q
интервЗJIОВ.
раздв.певннх
эиер
rиями
E~.
~=1,
...
,
6-1
(про6J1ему
рациОИ8JIЬноro
выоора
{E~3
IIВ
здесь
не
бу,цем
обсyzдатъ).
ка!щнй
энергетический
интервал
на
зывается
"rруппой,
и
номер
rpуппе
присваиваетCJI
по
зиачеВИJ)
.9-
на
границе
с
меньшей
.8верrиеА.
Поpgдок
нумерации
групп
таков,
Ч'1'О
при
возрастании
~.
эиерrин
умеиьшаетCSI.
т.е.
E:J
<.
Е
э
-
1
•
С.пе-
ДОИ8Т8J1ЬВО,
еCJJИ
нейтрон
pc»rд8втся
в'
результате
деления
В
rpYD-
пв
I,
то
ои
..
вт
затем
в
процвссе
замеДJIеllJla
перейти
из
rpyrIIIЬt
I
в
rpyппy
2,
затем
из
группн
2
в
группу
3
и
т.д.
ИJlИ,В
odщвм слу
чав,
из
rруппн
9f
В
rруппу
9 •
где
~
>9'·
•
После
TOro
как
раз
dиевие
энергетического
интервала
выбрано
(И,
ВОЗМОЖНО,
прове.цевн
ДОПOJПlИТeJlЬиве
веodхо.цимые
ИСCJJе.цования
и
расчетн~
мo1tвo
присту'
ПИТЬ
R
получеИИl)
ураввеНИI
мвоroгруппового
прИdJJ:Dеиия.
И
ДJUI
8rol
Ц8JDI
ecn
весиOJIЬИО,
способов.
мы
рассмотрим
JJИIDЬ
JtВa
из
ша.
ЗвJt8
....
ва
R8JЩОМ
из
ивтерва.пов
(E~)
Е
~_.,)
OOOneTO'l'BYUQyIJ
фуВ1CЦИlJ
Ч',СЕ)
t
котораа
вив
a'l'Oro
интерВaJIa
равна
ИУJШ,
а на
(Е
3'
Е,-1)
имеет
иехотоpнl
"пpoфuъ"
(1ИСо
5).
ВН6ерем.цJ1Я
ОIIpeдел&в':
~
воожи
следyпцylJ.
нормировку
этих
функций:
%(Е
1
E
I
-
1
!
Ч's(Е)d.Е=1,
~=1
•...
,G.
..
. .
Кроме
'1'01'0 t
aвaJ10rичвнм
odраэом
эа.ца.цим
еще
о.цву
СИСТeJq
фушщий
{
11';
(E)}:=i
ДJШ
хоторнх
привимае'1'ОЯ
та
же
вормиров-

,.
~
- 27 -
ка
(5.!).
~
D
\11;
(Е)
равна
ИfJ11)
8118
(E
S
I
E~-1
)
.,
ВО8-
IIIOIIIIO?
O'f.D1l88Т01!
0'1'
0/
~
(Е)
профв.пем
(И8
JlCIUIIJ1J88~~
oqчaI
4'3
=Ч';
).
в,дем
исиап
приБJlD8ввое
peIП81Q18
аада
...
(1.1)-(1.3)
в
....
е
G . . .
_
~
liJ
.Q
i
tt
-
L.
ч>
(t._.
)о/о(Е»)
(5.2)
G
8=1
; .
t1
Q8
II8IISВ80'1'l1К8
ФI~
ер
(J)
(!
,Q
t t)
ODpeД8JDDI
()
ПОМOJlP,l)
8'lO-
..
I'uePKllBa-ПеIfРОва.
СИО!'811а
ypaJlИ8md>.
1ЮЗ!lJlJr8_'I
в
8'f01I
__
8fO'-.
,
DpJDI8П'1'8JlЪRО
К
II81II81
аца"е
JDlее!'
....
j
clE
(
~(E)
~f
-+-
(Q,
V)
Ч>
G ...
L:t.
Ч'(Т'-
:D
E
.
-G
J
dE'J
r1Q'(i:.sTLi.t~L.j
)'Р
с;.
l.r,Q:-Е;i)-
:D
e
,
2
-
fэ-fс
)ЧJ;<Е)dЕ=О:
JclE(te
-If.
)ч/'О-(Е')
пpI(.!Еd])
JI-
(~,!1J<O:
:It
с;.
r
В
1
clE
(
'Рс;.
-If
a
)
Ч';
(Е)
=0
при
t
=0
,
,
:D
e
~
: i J •
••
J
G;
IIJJИ,
Ч'1'О
одно
• 1'0
ив,
.
,,"
(S>
,
'G
.L
~
+
'с
Q )
(j)
"(',)
(6) .
~,'
~
J"Q'
(f<J)
dt
_
.,
\1
\f
+
L..
tf
=4--
L-.
а.
1с
t.
gr
9'-"
.Q
IC
(i
J
(
го
Q'
t)
,2:
(В"В>(Г"
,,_
t)
+
,<9'+
p('~
Ч'
-'_
t
-'J~,
1з
i,;
(5.3)
(5.4)
(5.5)
..
при
.r
Е
dD
и·
(.Q,!!J.<o;
при
{=о
J 3
~!,
... , GJ
(5.7)
(5.8)
r.цe
.
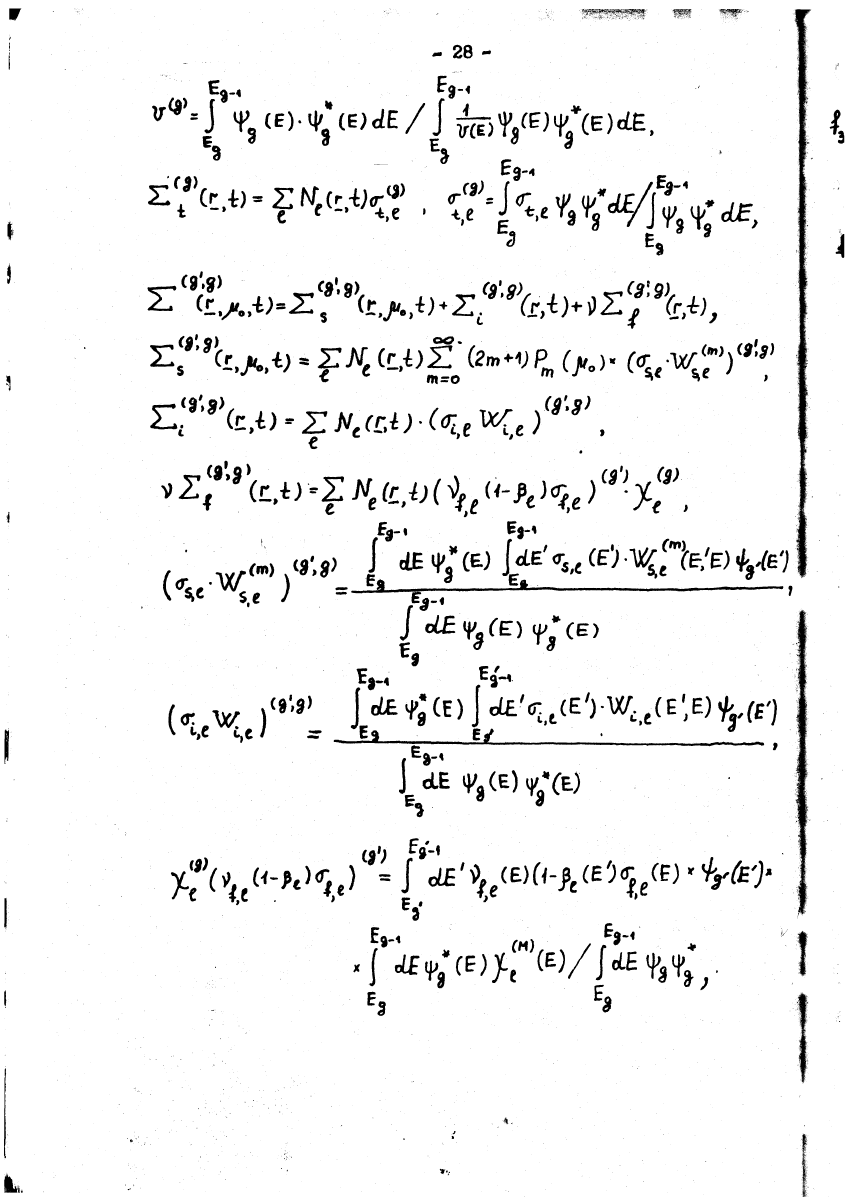
IJ
"":

')
-
29-
.
(5.9)
,
JI
~
(C,E,E-'.,.,i)
-~;
)
Ч',
(Е)
olE;
(6.10)
JJE'
(Ч';
-
Ч';
)СР,(Е)=-о
црв
,.~~D
•
(.Q.~
»0;
(5.П)
:t>e -
J
cil:
(
Ч';
-~*
)
'Уз(Е)=О
IIPJI
f.
='r. (5.12)
:J)e
Задачу
(5.10)-(5.12.)
ft«)DO
ЦPЦC'l8D5
'f8D8.
В
форм
-~
~<i~
~
(Q.
\1
)lf
з
*
+2:
(j~4f
..
~
LJJ.Q
'х
"
dt
t 8
4а-
з'st
.Q.
(5.13)
/
