Афанасьев А.А. Математические основы теории систем управления
Подождите немного. Документ загружается.

где
α
-вещественное число.
Множитель характеризует рост функции (6.7). Если
0>
α
α
,
то, очевидно, эта функция стремится к есконечности при
∞
→
t
б ;
если
0<
α
, то стремится к нулю прифункция
∞
→
t
.
Число
α
называется характеристическим показа унк-
ции (6.7).
телем ф
ТЕЛИ ЛЯПУНОВА
Пусть
6.2.1. ХАРАКТЕРИСТИЧЕСКИЕ ПОКАЗА
()
tx
ϕ
=
- некоторая веществе
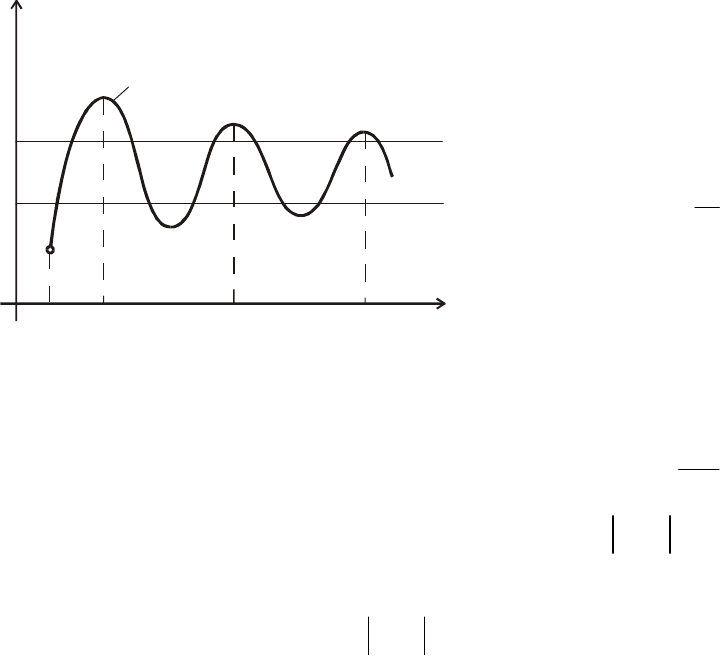
торой показан на рис. 6.1.
д
нная функция, график ко-
Если ля некоторой последовательности
),2,1( K=
∞
→t
k
существуе
k
т конечный или бесконечный предел определенного зна-
а к
(
)
ta
k
k
ϕ
= lim
,
∞→
то функции число называется частичным пределом
a
()
t
ϕ
при
∞
→
t
.
Наибол ий
ных предело
ьш из частич-
в функции
aSup
x
α
=
еде-
называется ее верхним пр
лом:
()
t
t
ϕ
=
α
∞→
mli
.
Аналогично определяется
предел функции
нижний
(
)
t
ϕ
при
∞
→
t
как наименьший
частичных пределов:
из
ее
()
t
t
ϕ
β
∞→
=
lim
.
функции Модуль комплекснозначной
(
)
tf
можно предста-
вить в показательной форме
(
)
(
)
tt
etf
α
=
.
t
ерхний и ниж ункции
α
β
ϕ
()
t
t
1 2
t
0
t
3
t
0
Рис. 6.1. В ний пределы ф
80

Отсюда
()
(
)
t
tf
t
ln
=
α
.
Исследуя рост модуля функции
(
)
tf
на полуоси
∞
<
< tt
0
коэффициента
, ес-
тественно интересуются максимальным значением
()
t
α
.
Число
[
]
fχ
, определяемое по формуле
(
)
[]
t
t
m
f
f
ln
=χ
называют верхним характери
функции .
Аналогичным образом можно
нижний характеристический пок
t
li
∞→
(6.8)
стическим показателем Ляпунова
было бы ввести в рассмотрение
азатель Ляпунова функции
()
tf
(
)
tf
по
[]
15
формуле
[]
(
)
t
tf
ln
∞
, (6.9)
не пользуются
f
t
lim
→
=χ
′
но обычно, следуя Ляпунову, им
[
]
16
.
Свойства характеристических показателей Ляпунова
1
Из формулы (6.8) следует:
1.
()
[]
()
[
]
tftf χ=χ
.
2.
()
[]
()
[
]
tftcf χ=χ
.
3.
Если , то
()
[]
±∞≠α=χ tf
(
)
1lim =
∞→
t
t
e
tf
α
.
Следовательно, для любого
0>
ε
1
Рассматриваемые иногда характеристические числа Ляпунова отличаются
только знаком от показателей (6.8) [53].
81
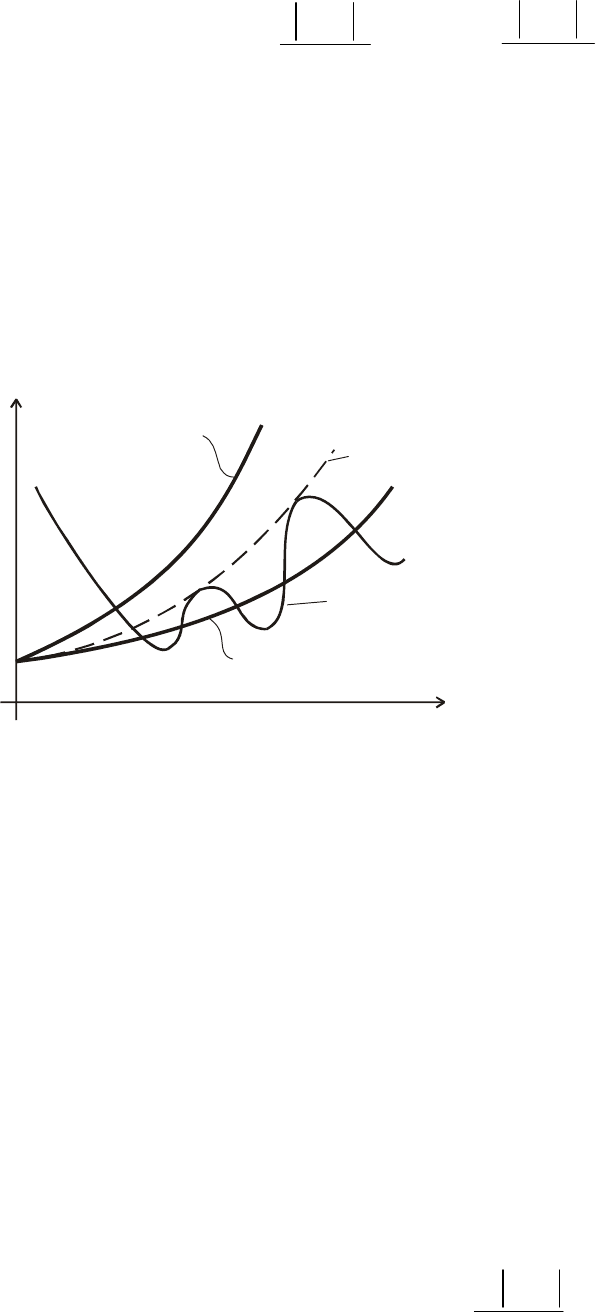
()
0lim
)(
=
+
∞→
t
t
e
tf
εα
,
(
)
+∞=
−
∞→
t
t
e
tf
)(
lim
εα
.
Таким образом, если
()
[]
α
=
χ tf
, то модуль фун
медленнее любой показательной функции
кции
()
tf
растет
t
e
x
)(
ε
+
α
=
и быстрее любой показательной функции (рис. 6.2)
t
e
x
)(
ε
α
−
=
.
4.
Характ
суммы конечного числа
функций
еристический показа-
x
тель
(
)
tf
k
()
mk K,2,1=
не
из
е
падает
шим
⎡
превышает
характеристических пока-
лей эти
с ним, если наиболь-
характеристическим
о из слага
m
⎤
5. оказатель ечно о числа
функций
()
e
(
αε
+)
t
e
(
наибольшего
зат х функций (сов-
показателем обладает лишь
одн емых):
() ()
[]
tftf
k
k
k
k
χ≤
⎥
⎦
⎢
⎣
χ
∑
=
max
1
.
Характеристический п произведения кон г
(
)
не превышает суммы характери-
стических функций:
.
6.
Назовем характеристический показатель функции
гим, если существует конечный предел (независимо
mktf
k
K,2,1=
показателей этих
() ()
[]
∑
=
=
χ≤
⎥
⎦
⎤
⎢
⎣
⎡
Πχ
m
k
kk
m
k
tftf
1
1
() ( )
0
tttf >
от вида стро
числовой последовательности
∞
→
k
t
):
()
[]
(
)
t
tf
tf
t
ln
lim
∞→
=χ
. (6.10)
e
α
t
x
=
⎟
f
(t)
⎟
α
ε
)
t
–
1
t
0
Рис. 6.2. К анализу роста модуля функции ft
c помощью характеристического показателя
Ляпунова =ft
()
[()]
αχ
82

В этом случае верхний (6.8) и нижний (6.9) характеристические
показатели функции совпадают и равн
ы (6.10):
()
(
)
(
)
ttt
t
t
t ∞→
∞→
∞→
tftf
ln
liml
=
ункций
()
и
()
сумме характеристических показателей этих
tf
ln
lim
ln
mi
=
. (6.11)
7.
Если функция
()
tf
имеет строгий характеристический показа-
тель, то характеристический показатель произведения ф
tf
функций
tg
:
равен
()
(
)
[]
(
)
[
]
(
)
[
]
tgtftgtf
χ
+
χ
=
χ
. (6.12)
(
)
tf
(
)
∞
<
<
tt
8.
Под интегралом функции
0
, следуя Ляпуно-
ву, будем понимать:
()
, если
( )
∫
=
t
t
dftF
0
ττ
(
)
[
]
0≥
χ
tf
, (6.13)
, если
() ( )
∫
∞
= dftF
ττ
(
)
[
]
0
<
χ
tf
t
. (6.14)
9.
интеграла не превышает
характеристического показателя подынтегральной функции
Действительно, пусть
Характеристический показатель
(
)
[
]
α
=
χ
tf
, тогда для любого
0>ε
(
)
()
0lim =
ε+α
∞→
t
t
e
tf
.
Следовательно,
(
)
(
)
t
etf
ε
α
+
Μ<
,
де
0>Μ
. г
а) Полагаем
0>
α
, тогда из (6.13) имеем:
(
)
()
() ()
()
[
]
()
ε+α
Μ
<
ε+α
ε+
t
t
t
t
t
t
e
tF
0
00
.
−
ε+α
=τΜ<τ≤
α
ε+ατε+α
∫∫
t
eededtf
Μ
83

Таким образом,
[]
ε
+
α
≤
χ )(tF
.
Так как произвольно, то
(
)
[
]
(
)
[
]
α
=
χ
≤
χ
tftF
0>ε
.
б) Аналогично доказывается утверждение и при
0
<
α
.
1 конечной матрицы
()
[]
tA
0. Характеристический показатель
рис ическим псовпадает с характе т оказателем ее нормы
()
[]
(
)
[
]
tt AA
χ
=
χ
,
где под нормой понимается одна
вы
11. Характеристический показатель суммы онечного числа матриц
не превышает наибольшего из характеристических показателей
,
матрицы одинакового размера, в том числе столб-
цовые (строчные). Так как
из четырех рассмотренных
ше норм ((5.86)-(5.89)).
к
этих матриц.
Пусть
()
[]
()
[]
∑
=
=
N
j
j
tAtA
1
где
()
[]
j
tA
-
()
[]
()
[]
∑
=
≤
N
j
j
tAtA
1
,
то
()
[]
()
[]
()
[
]
()
[]
j
j
N
j
j
tttt AAAA χ=χ≤χ=χ
∑
=
max
1
.
ический показатель произведения конечного числа
матриц не превышает суммы характеристических показателей
этих матриц.
12. Характерист
Характеристические показатели решений однородного
уравнения
Будем рассматривать однородное уравнение
84
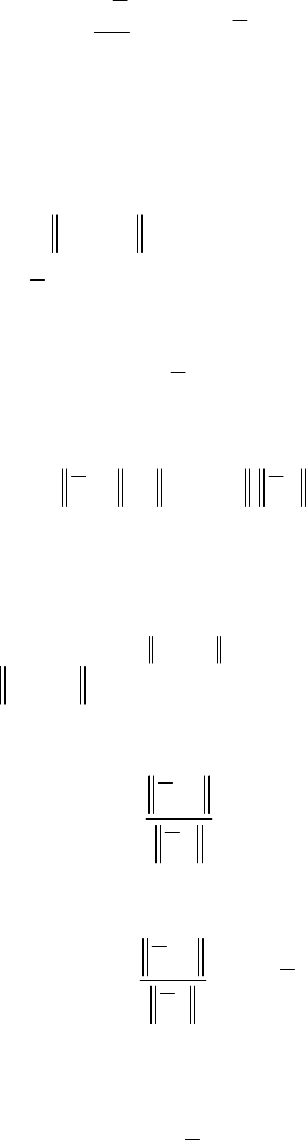
()
[]
xtA
d
t
xd
=
. (6.15)
6.3 (Ляпунова)
Если матрица кусочно - непрерывна и ограничена, т.е.
Теорема
()
[]
tA
(
)
[
]
const
=
≤
ctA
, (6.16)
о к
(
т аждое решение
)
tx
(
)
∞
<
<
tt
0
однородной системы имеет
ограниченный характеристический показатель:
(
)
[
]
ctxc
≤
χ
≤
−
. (6.17)
Действительно, в соответствии с (1.9) справедливо: формулой
(
)
(
)
[
]
0
xtxtx
≤
.
ного решенияПоскольку норма фундаменталь
()
[
]
tx
удовлетворяет,
с учетом (6.16), неравенству
()
[]
()
[]
()
00
ttc
dA
eetx
t
t
−
τ
∫
τ
≤
,
то будем иметь:
≤
()
(
)
(
tct
tx
−
)
tt–c −
00
0
e
x
e ≤≤
. (6.18)
Учитывая, что
(
)
()
[
tx
χ=
⎥⎢
χ
]
tx
⎤⎡
,
получим, находя характеристический показатель всех членов нера-
венства (6.18):
x
⎦⎣
0
(
)
[
]
ctxc
≤
χ
≤
−
.
Неравенство (6.17) справедливо ля любого из независимых
ских показателей решений системы при ограни-
ченности матрицы . Все они принадлежат
n
(6.15)
интервалу
д
решений системы (6.15). Из него вытекает конечность значений ха-
рактеристиче
()
[]
tA
[]
cc,
−
.
Рассмотрим теперь независимых решений
n
85

()
(
)
(
)
txtxtx
n
,,,
21
L
системы (6.15). Для каждого решения
(
)
tx
k
можно определить ха-
акте еский показателр ристич ь
()
[]
(
)
t
t
k
∞→
Множество всех характеристических показателей диффе-
ренциальной системы (6.15) называют ее спектром.
Если характеристические показатели расположим
t
tx
k
k
ln
mli
=χ=χ
. (6.19)
в порядке
возрастания, будем иметь:
x
m
χ
<
<χ<χ K
21
(
)
nm
≤
.
Их количество оказаться меньше
n
, т.к. некоторые может из них
огут совпадать друг с другом.
характеристические показатели
постоян-
ной м
м
Для стационарной системы
совпадают с енными част с веществ ями обственных чисел
атрицы
[]
A
:
jj
λ
=
χ Re
.
Замечание 6.2
ство э
ПРИМЕР 6.1
Нелинейная дифференциальная система может иметь
спектр произвольной природы, например сплошной, содержащий
бесконечное множе лементов.
Скалярное дифференциальное уравнение
)0,0(ln >>= xtx
t
x
d
t
dx
меет общее решение
,
где C– произвольная постоянная, и, следовательно, это уравнение обладает сплош-
ным спектром.
и
tC
ex =
86

6.2.2. ГЕНЕРАЛЬНЫЕ ПОКАЗАТЕЛИ
Введем в рассмотрение другую характеристику поведения
решений уравнения (6.15).
Пусть
[
]
0
)()( xtxtx
=
- какое-нибудь решение этого , где
[]
)(tx
- фундамен- уравнения
а
тальная матрица уравнения (6.15), для которой
[]
Etx >)(
. Назовем
верхним генеральным показ телем этого уравнения
[
]
)(tx
δ
=
α
α
точную нижнюю границу значений , при которы
стоянная такая, что выполняется условие:
х существует по-
0>
α
N
)()(
)(
τ
τ
α
α
xeNtx
t
−
≤
(6.20)
при любых
[
)
∞∈ ,0,t
τ
, таких, что
t
≤
τ
.
Если таких чисел
α
не существует, то полагают:
[
]
+
∞
=
)(tx
δ
.
)(
t
x
Аналогично, нижним генеральным показателем решения
[
]
)(tx
γ
β
=
азывают такую верхнюю границу значенийн
β
, при которых суще-
ствует постоянная такая, что выполняется неравенство:
0>
β
N
,)()(
)(
τ
τ
β
β
xeNtx
t
−
≥
+∞
<
≤
≤
t
τ
0
. (6.21)
Если таких чисел не существует, то полагают
[
]
−∞=)(tx
γ
.
одно Неравенства (6.20), (6.21) можно объединить в
)()(
)(
αβ
τ
x
,
)(
τατβ
−−
≤≤
tt
eN
tx
eN
+∞<
≤
≤
t
τ
0
, (6.22)
откуда следует соотношение
α
β
≤
.
Очевидно, что значения показателей не зависят от способа
определения нормы комплексных векторов.
87
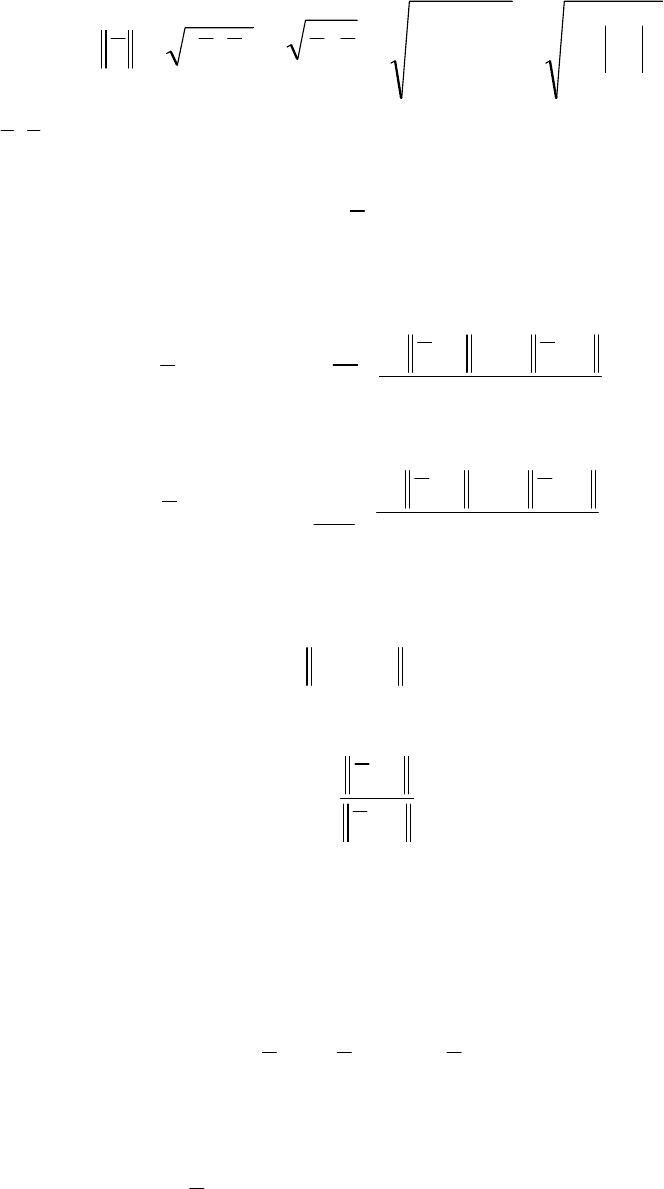
В качестве нормы можно взять длину (модуль) вектора
()
∑∑
==
∗∗
====
n
j
j
n
j
jj
xxxxxxxx
1
2
1
,
,
где
()
yx, - скалярное произведение векторов.
Замкнутый интервал
[]
α
β
,
называется интервалом гене-
ральных показателей вектора
)(
t
x
на оси
+
∞
<
<
t
0
.
Нетрудно проверить,
справедливы формулы:
обращаясь к выражению (6.22), что
−
τ
[]
=α=δ
→τ
−
tx
t
l)(
τ−
∞
∞→τ
t
xtx
)(ln)(ln
mi
, (6.23)
[]
−
τ
τ−
=β=
xtx
x
)(ln)(ln
для е
γ t)(
∞→τ
∞→τ−
t
t
lim
. (6.24)
Если системы уравнений (6.15) выполнено соотношени
[]
CtA
≤
)(
,
то аналогично формуле (6.18) справедлива о
()
ценка:
()
τ−τ−−
≤
τ
≤
tCtC
e
x
tx
e
)(
)(
. (6.25)
Из нее вытекает конечность генеральных по лей и оценка для
них:
казате
C
C
≤
≤
≤
−
α
β
.
Обратимся теперь к независимым решениям
)(),(),(
21
xtxtx
n
K t
системы (6.15), столбцы (векторы) которых образуют матрицу фун-
даментального решения.
я ка
)(t
Дл ждого
x
k
строим по формулам (6.23), (6.24) ин-
тервал генеральных показателей
по
[
]
kk
α
β
,
. Расположим эти интер-
валы на числовой оси
σ
генеральных показателей (рис. 6.3).
88
у интервалы а
на друга, с разделяться от
рые называют регулярности
бе неральных
показателей, также относят к интервалам регулярности.
елей
назы ных
уравнени
Для стационарной сис-
емы
ных показателей вырожда-
тся в точки, совпадающие
частями
исел
янной матрицы .
Отметим важнейшие свойства енераль
шений нестационарного дифференциального уравнения [15,44]:
1.
Пусть
Замкн тые показ телей могут накладываться друг
овпадать и крытыми интервалами, кото-
интервалами [44]. Правую и левую
сконечные полуоси, примыкающие к интервалам ге
Множество замкнутых интервалов генеральных показат
вают спектром решений системы линейных нестационар
й (6.15).
[ ] [ [ ] ]
βα
1 1
β β α α
23 2 3
β β α α
45 4 5
[ ]
σ
Рис. 6.3. Возможные интервалы генеральных
т интервалы генераль-
ю
с вещественными
собственных ч посто-
показателей матрицы фундаме
решения с n=5
нтального
[]
A
г ных показателей ре-
)(
t
x
k
const=
k
. Тогда показатели вектора генеральные
совпадают генеральными показателями вектора
)(
t
x
.
2.
Верхний генеральный пока
)()(
2
затель суммы
1
txtx +
не превы-
шает верхних генеральных показателей векторов
)(),(
21
txtx
и
равен наибольшему из них, если эти показатели различны.
3.
Нижний генеральный показатель ммы су
)()(
21
txtx +
не меньше
нижних генеральных показателей векторов
)(),(
21
txtx
и равен
наименьшему показателю, если эти показатели различны.
4.
Характеристический показатель вектора
)(
t
x
находится внутри
интервала генеральных показателей
[
]
[
]
[
]
)()()( txtxtx
δ
≤
χ
≤
γ
.
5 и .
Есл
[
(
]
0)
0)(lim
=
∞→
tx
t
<
δ tx
, то , причем стремление к нулю име-
ет экспоненциальный характер.
89
