Афанасьев А.А. Математические основы теории систем управления
Подождите немного. Документ загружается.

)
]
() (
[
()
()
0,, >=
∫
+∞
atGty
c
τ
. (6.102)
(6.98) от знака .
При , когда объект (6.97) устойчив, статическую характеристику (6.98)
енно возрастает.
Покажем тем не менее, что статическая характеристика (6.98) и в случае неус-
тойчивого объекта имеет вполне определенное физическое значение и даже может
ю усло-
Действительно, предположим, что объект (6.98) включен в состав замкнутой
устойчивой системы.
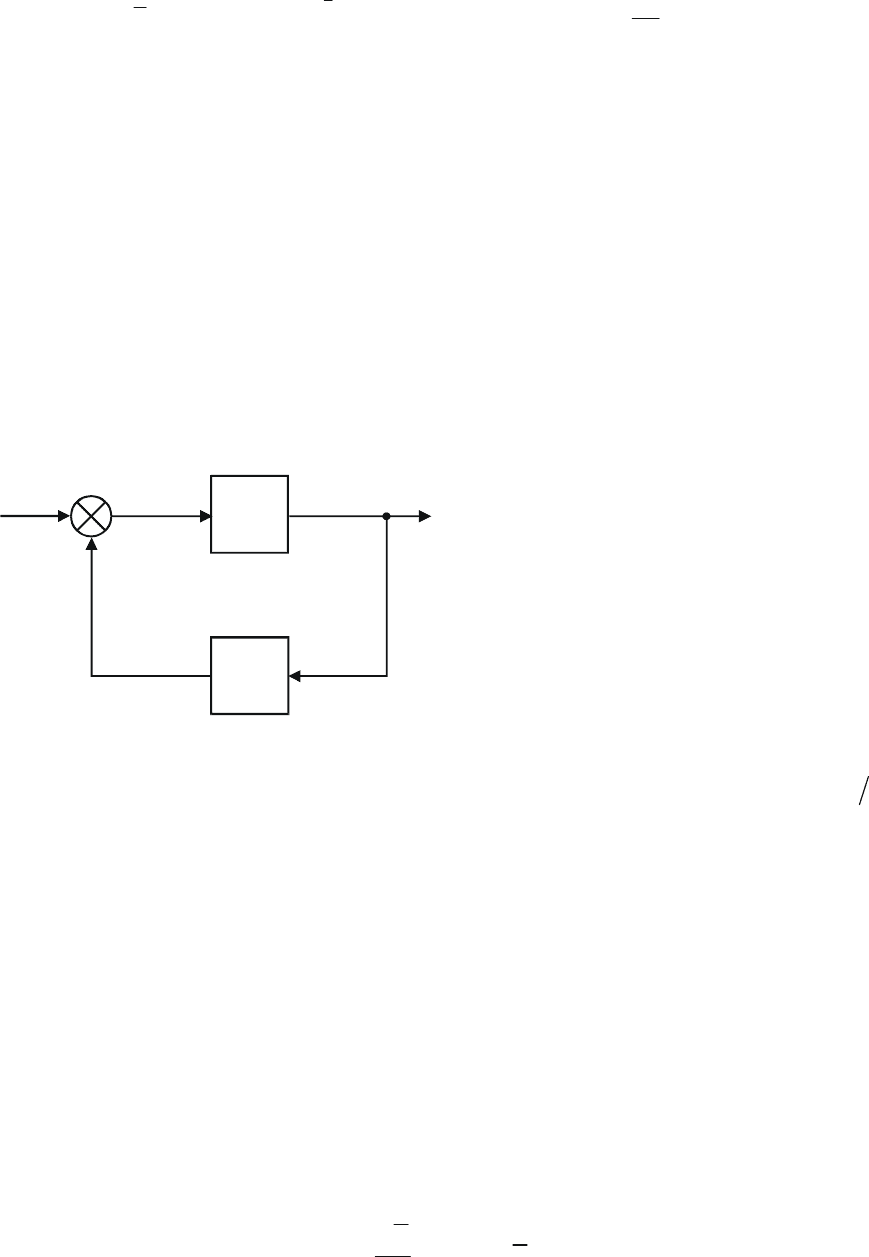
На рис. 6.8 элемент I означает объ-
- соответствующую цепь
−=−=
∫
∞
−
f
dfedf
c
ta
τττ
τ
a
tt
Видим, что формулы (6.101) и (6.102) приводят к одному и тому же результату
независимо
a
0<a
можно получить экспериментально, подавая на его вход постоянный сигнал и за-
меряя сигнал выхода после затухания переходного процесса.
При
0>a
такой эксперимент становится невозможным, так как переходный
процесс в системе неогранич
быть получена экспериментально, если соответству щим образом изменить
вия эксперимента.
ект, а элемент II
коррекции.
g
z
f
I
Если
const
=
=
c
gg
, то в силу ус-
тойчивости в замкнутой системе можно
наблюдать установившийся процесс
const
II
y
Рис. 6.8. Устойчивая замкнутая система
=
=
c
y y
,
const=
=
c
zz
const
,
=
=
c
При этом очевидно отношение
f f
.
cc
fy
не
будет зависеть от входного сиг
нала системы и вида звена коррекции II.
Таким образом, описанный эксперимент фактически дает способ физической
реализации уравнения (6.102) при .
Удобство нахождения статической характеристики объекта по формуле (6.96)
(в данном случае по формуле , что появляется возмож-
ность исследования установ средственно по исходному
равн
оторые понятия, связанные с поведением решений
уравнения
с неустойчивым объектом
I
c
g
0>a
(6.102)) заключается в том
ившихся процессов непо
у ению объекта независимо от его устойчивости или неустойчивости.
6.5.9. УСТОЙЧИВОСТЬ И БИУСТОЙЧИВОСТЬ
Введем нек
()
[]
xtA
d
t
xd
=
(6.103)
на полуоси .
[
)
∞,0
110
1. Устойчивость вправо
Уравнение (6.103) называется устойчивым (точнее, устойчи-
вым вправо), на полуоси
Необходимым и достаточным условием устойчивости уравне-
ия (6.103) является равномерная огранич
решения
если каждое его решение ограничено
[
)
∞,0
.
н енность матрицы фунда-
ментального
(
)
[
]
∞
<
≥t 0
В этом случае существует постоянная , такая, что
txSup
.
0>q
(
)
(
)
0xqtx
<
.
2. Уст ойчивость влево
Назовем уравнение (6.103) устойчивым влево, если существу-
ет постоянная
0>
′
q
, такая, что для любого решения
()
tx
этого
уравнения при всех
0≥
t
выполняется оценка
(
)
(
)
txqx
′
≤
0
.
Устойчивость влево, очевидно, эквивалента равномерной ог-
раниченности матрицы
(
)
[
]
1−
tx
(
)
[
]
∞<=
′
−1
≥0
Sup txq
t
.
3. Биустойчивость
Назовем уравнение (6.103) биустойчивым на полуоси
[
)
∞
,0
,
если оно устойчиво и вправо, и влево
Таким образом, уравнение (6.103) биустойчиво тогда и толь-
.
ко тогда, когда
(
)
[
]
∞<
±
∞<≤
1
0
Sup tx
t
,
или, что равносильно, когда
111

(
)
[
]
∞
<
τ
∞<≤
,Sup
0
tH
t
.
4. Интегрально сравнимые уравнения
Пусть на полуос ния и
[
)
∞,0
заданы два уравне
()
[
]
()
2,1=kx
dt
k
. (6.104)
азовем эти уравнения интегрально
= tA
xd
Н сравнимыми, если выполняет-
ся условие
()
[]
()
[]
∞<−
∫
∞
dttAtA
0
12
.
Лемма 6.1
Если одно из двух интегрально сравнимых уравнений (6.104)
равномерно устойчиво вправо (влево) или биустойчиво, то соот-
ветствующим свойством обладает и второе уравнение [10].
Рассмотрим, в частности, уравнение
()
[]
xtA
xd
=
dt
,
ля матрицы которого справедлид во
()
[]
tA
()
[]
∞<
∫
dttA
0
.
∞
Это уравнение интегрально сравнимо с биустойчивым уравнением
0=
xd
dt
следовательно, и оно биустойчиво.
5. Асимптотически эквив
ния (6.104) ас
если между их решениями
ное соот вие ения
,
алентные уравнения
Назовем уравне имптотически эквивалентными,
можно установить взаимно однознач-
ветст притяж
(
)
(
)
txt
2
x
1
↔
таким образом, что
112
(
)
(
)
[
]
0lim
12
=
−
∞→
txtx
t
.
Признак асимптотической эквивалентности линейных диффе-
ренциальных систем устанавливается следующей теоремой.
нсона)
Пусть решения системы
Теорема 6.8 (Леви
[]
xA
dt
где
[]
A
- постоянная матрица, ограничены на полу
xd
=
, (6.105)
оси
[
)
∞
,0
. То-
гда система
[]
()
[]
ytByA
yd
+=
, (6.106)
dt
где
()
[]
∞<dt
∫
∞
tB
,
стеме (6.105) [16].
0
асимптотически эквивалентна си
Следствие
Пусть
()
[]
ytB
yd
dt
где
()
[]
tB
абсолютно интегрируема на
=
, (6.107)
[
)
0, ∞
. Тогда каждого
решен
для
ия
()
ty
существует
()
C
t
=
∞→
, (6.108)
C
i
i
y
tylim
т.е. все интегральные кри-
вые
()
tyy =
имеют горизонталь-
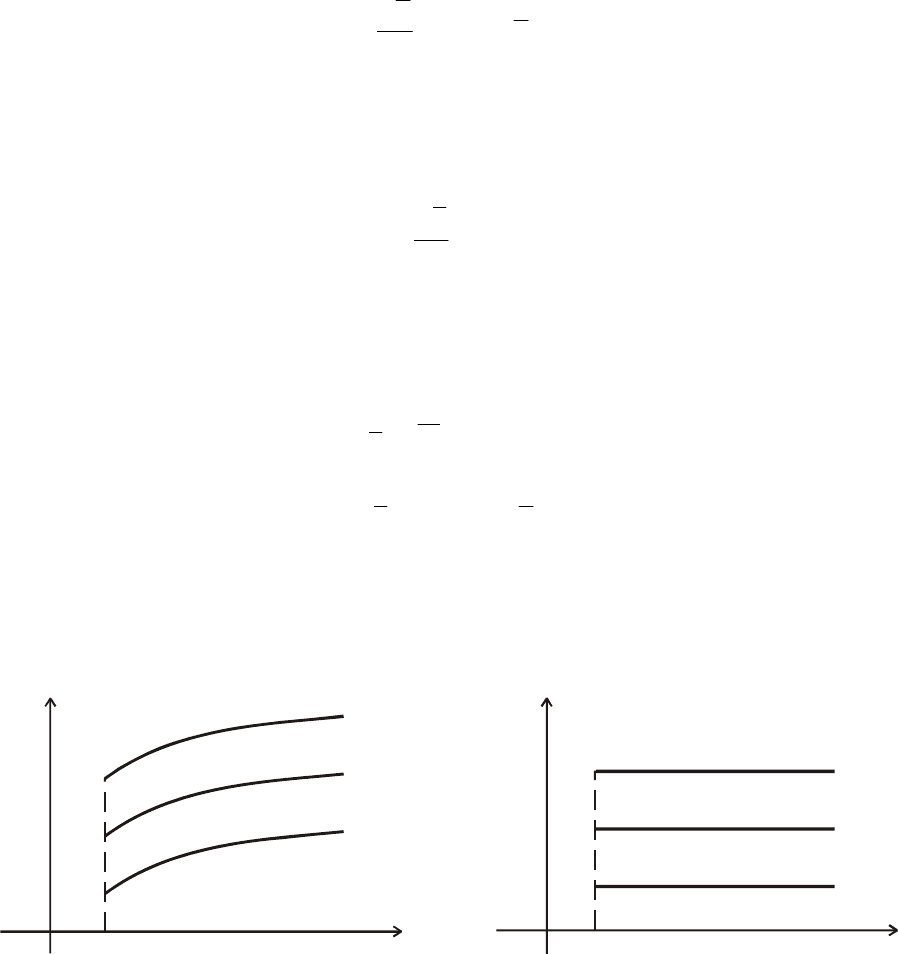
ные асимптоты (рис. 6.9), причем
различные интег
yyt
ii
=()
ральные кривые
t
0
Рис. 6.9. Асимптотика решений
уравнения состояния (6.107)
()
tyy
1
=
и
()
tyy
2
=
имеют раз-
ые горизонтальные асим-
птоты
личн
11
C=
и
y
2
C
и сверх
1
y =
113
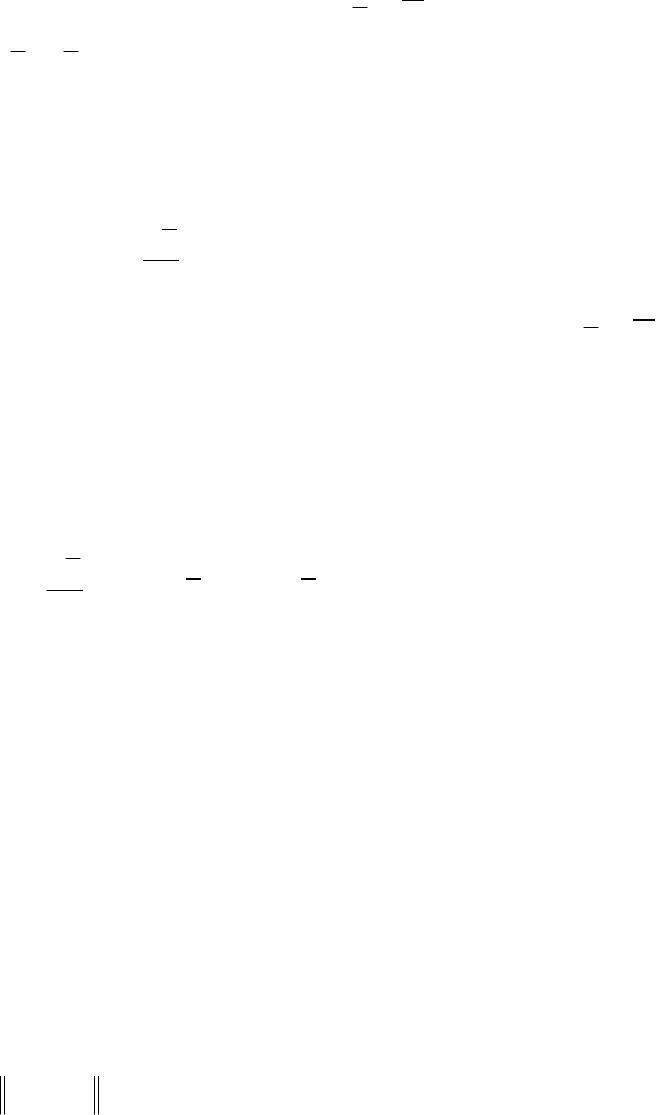
Cy =
того, для каждой горизонтальной прямой существует ин-
тегральная кривая
()
tyy =
, имеющая эту прямую своей асимпто-
ой. т
Действительно, в силу теоремы Левинсона система (6.107)
асимптотически эквивалентна системе
0=
dt
xd
(6.109)
с матрицей . Так как система (6.109) имеет решения
[]
0=А
C
x
=
,
то от
.5.1 ОГО РАСЩЕПЛЕНИЯ
Рассмотрим наряду с исходным уравнением (6.103) уравнение
сюда вытекает предельное соотношение (6.108).
6 0 УСТОЙЧИВОСТЬ ЭКСПОНЕНЦИАЛЬН
()
[]
()
[]
xtBxtA
dt
xd
+=
, (6.110)
оторое будем называть возмущенны
невозмущенным
Теорема 6.9
Пусть уравнение (6.103) допускает экспоненциальное расще-
пление порядка и пусть
к м (исходное уравнение (6.103)
будем называть ).
nm ≤
[]
[
]
mmm
δ
γ
δ
γ
,,,
111
=
Δ
=Δ K
- интерв х показателей независимых решений урав-
нения (6.103). Тогда для любого сколь угодно малого
алы генеральны
0>
ε
су
вует
щест-
такое, что при любой матрице
(
)
[
]
t
,
B
0)( >
ε
δ
удовлетво-
ряющей условию
()
[
]
(
)
+
∞
<
<
∞
−
< ttB ,
ε
δ
,
енное уравнение (6.110) бувозмущ дет допускать экспоненциальное
генеральных показателей,
таких, что если
расщепление порядка
m
с интервалами
[]
[
]
mmm
δ
′
γ
′
=
Δ
′
δ
′
γ
′
=
Δ
′
,,,
111
K
,
то
114
[] []
ε<
′
−
i
i
PP
.
ε<δ
′
−δε<γ
′
−γ
iiii
;,
Из этой теоремы [44] следует, в частности, устойчивость ге-
неральных показателей и проекторов экспоненциально-
ихотомического расщепления по отношению к м
ниям коэффициентов дифференциального уравнения.
воря,
Осуществим в однородном уравнении
д алым возмуще-
Необходимо также отметить, что характеристические показа-
тели решений, вообще го не являются устойчивыми [10].
6.6. КИНЕМАТИЧЕСКИ ПОДОБНЫЕ УРАВНЕНИЯ
()
[]
xtA
dt
xd
=
(6.111)
замену переменных
(
)
[
]
xtCz
=
, (6.112)
где матрица
()
[
]
tC
непрерывнодифференцируема и удовлетворяет
следующим условиям:
()
[]
(
)
[
]
const;const =≤=≤ d
dt
gtC
(6.113) 1)
tCd
на промежутке
[
)
∞
,
0
t
.
2) . (6.114)
Матрицы , обла , на-
зываются матрицами Ляпунова.
Нетрудно показать, ч
()
[]
0det >≥ ftC
()
[]
tC
дающие свойствами (6.113), (6.114)
то если
(
)
[
]
tC
- матрица Ляпунова, то
()
tC
[]
1−
также матрица Ляпунова.
Дифференцируя (6.112), получим:
(
)
[
]
()
[]
dt
xd
tCx
dt
tCd
dt
zd
+=
.
Исключая отсюда
x
с помощью (6.111) и (6.112), имеем:
115

()
[]
ztB
zd
=
dt
, (6.115)
где
()
[]
()
[]
()
[]
()
[]
()
[]
()
[]
11 −−
+= tCtAtCtC
dt
tCd
tB
. (6.116)
Уравнения (6.111) и (6.115) называются кинематически по-
на интервале , если между
ешений этих уравнений установит
оответствие (6.112) с матрицы
добными совокупностями всех
р ь взаимно однозначное
[
)
∞,
0
t
можно
помощью
()
[
]
tC
. с Ляпунова
Если имеем
()
(
)
[
]
0
xtxtx
=
,
то из (6.112) получим:
() ()
[]
()
[]
(
)
[
]
(
)
[
]
(
)
[
]
0
1
0
0CtxtCxtxt = zCtz
−
=
.
Следовательно, фундаментальная матрица уравнения (6.115)
()
[
]
()
[]
(
)
[
]
(
)
[
]
1
0
−
= CtxtCtz
. (6.117)
Из (6.117) имеем также
()
[
]
(
)
[]
(
[
)
]
(
)
[
]
11 −−
τ
C
.
1
0
−
=
ττ
xCz
Отсюда получаем выражение для матрицы Коши уравнения (6.115)
()
[]
()
[]
()
[]
(
)
[
]
(
)
[
]
(
)
[
]
11
,,
−−
=
τττ
CtHztztH =
τ
tC
Z
, (6.118)
де г
()
[]
()
[]
()
[
]
1
,
−
=
ττ
xtxtH
- матрица Коши уравнения (6.111).
0
ные показатели [10].
Теорема 6.1
Уравнения, кинематически подобные на полуоси, имеют оди-
наковые характеристические показатели и одинаковые генераль-
116

Теорема 6.11
Кинематически подобное уравнение (6.115) экспоненциально -
дихотомично на оси в том и только в том случае, когда этим
свойством обладает исходное уравнение (6.111). При этом, если
]
2
P
- проекторы, задающие дихотомию в исходном уравне-
нии, то соответствующие проекторы ля уравнен
ют вид [44]:
[]
1
P
и
д ия (6.115) име-
[
[]
(
)
[
]
[
]
(
)
[
]
1
1
00
~
1−
, (6.119)
= CPCP
[]
~
(
)
[
]
[
]
(
)
[
]
00
1
2
2
−
= CPCP
. (6.120)
6.7. ПРИВОДИМЫЕ У
6.
Нестационарное уравнение (6.111) н
япунову, если оно кинематически под
РАВНЕНИЯ
7.1 ТЕОРЕМА ЕРУГИНА
азывается приводимым по
Л обно стационарному урав-
нению
[]
zB
dt
zd
=
, (6.121)
актеристический и верхний генеральный показатели при-
водимого уравнения совпад
где
[]
const=
.
B
Теорема 6.12
Хар
ают [10]
[
]
[
]
zz
δ
=
χ
.
Эти показатели являются строгими.
Действительно, в соответствии с теоремой 6.10 справедливо:
[]
[
]
[
]
[
]
[
]
[
]
zzzxzx
χ
=
δ
=
γ
=
δ
χ=χ ,
.
Н.П. Еругиным получены необ дихо мые и достаточные условия
приводимости уравнения (6.111).
117
Теорема 6.13 (Еругина)
Линейная дифференциальная система (6.111) приводима то-
гда и только тогда, когда некоторая ее фундаментальная матри-
а может быть представлена
умноженной на экспоненциал произведения независимой
ц в виде матрицы Ляпунова
()
[]
tx
()
[]
1−
t
,
C
переменной t на постоянную матрицу
[
]
B
, т.е. [16]
()
[]
(
)
[
]
[
]
tB
1−
etCtx =
. (6.122)
Доказател
ий
.111) приводима, т.е. с помощью замены
ьство
Докажем необходимость услов теоремы Еругина. Пусть
система (6
(
)
[
]
xtCz
=
(6.123)
реобразуется в стационарное уравнен
орого
п ие (6.121), фундаментальное
)(
t
z
удовлетворяет матричному уравнению решение кот
()
[
]
[]
()
[]
tzB
d
t
tzd
Его решение имеет вид
=
. (6.124)
()
[]
[
]
[
]
tB
eDtz =
, (6.125)
где - произвольная неособенная постоянная матрица. Выбрав
из формул (6.123), (6.125) получим выражение (6.122).
Достаточность условий теоремы также доказывается неслож-
но [16].
Теорема 6.14
Приводимая линейная однородная система асимптотически
устойчива тогда и только тогда, когда все ее характеристиче-
ельство вытекает из того, что характеристические по-
системы совпадают с вещественными частя-
ми собственных чисел матрицы
[]
D
E
,
[]
D =
ские показатели отрицательны.
Доказат
казатели приводимой
[
]
B
.
118
6.7.2. ПРИВОДИМОСТЬ К НУЛЕВОЙ МАТРИЦЕЙ
система
СИСТЕМЕ С
Пусть линейная
()
[]
xtA
xd
=
, (6.126)
dt
,
с помощью преобразования Ляпунова (6.112) преобразуется в сис-
тему
где
()
[]
tA
- ограниченная, непрерывная, действительная матрица
0=
d
t
zd
(6.127)
с нулевой матрицей
[]
B
(матрица
[
]
B
представлена формулой
(6.116)).
Общее решение систем ь ы (6.127) ест
const
=
=
C
z
. (6.128)
Поскольку
[
(
)
(
)
]
(
)
txtCtz
=
,
то из (6.112), (6.113) и (6.128) следует, что решение системы (6.126)
ограничено.
Характер решений исходной сист
на рис. 6.10.
а)
б)
t
0
0
t
Р Решения исходного (а) и приведенного (б) уравнения состояния.
x
z
t
0
t
0
ис. 6.10.
емы и приведенной показан
119
