Афанасьев А.А. Математические основы теории систем управления
Подождите немного. Документ загружается.

1) С нулевым собственным значением
)0(
1
=
λ
. Если это значение
простое, то система (5.7) имеет ограниченное решение, и значит,
она устойчива по Ляпунову. Если значение
0
1
=
λ
кратно, то сис-
тема (5.7) неустойчива.
2) С парой чисто мнимых значений
ω
±
=
λ
j
2,1
, кратность которых
равна или больше единицы. Характер устойчивости аналогичен
предыдущему случаю.
3) С бесконечно удаленным собственным значением . Эта
точка также очевидно принадлежит границе между левой и пра-
вой полуплоскостями.
∞=λ
1
Первый тип границы называют иногда апериодическим, по-
скольку частота мнимого значения
1
λ
равна нулю, второй - коле-
бательным (периодическим).
Устойчивость системы (5.7) является ее внутренним свойст-
вом (определяется местом нахождения собственных значений мат-
рицы - в левой полуплоскости). Она не зависит от начального
значения переменных . Такую устойчивость называют
устойчи-
востью в целом (или "в большом").
[]
A
0
x
Таким образом, для асимптотической устойчивости уравне-
ний состояния (5.7) необходимо и достаточно, чтобы собствен-
ные значения матрицы
[
, являющиеся корнями векового уравне-
ния , обладали отрицательными вещественными час-
тями.
]
A
[][
EA λ−det
]
Вековое уравнение может быть развернуто в виде характери-
стического полинома
0
1
10
=++λ+λ
−
n
nn
aaa K
(5.9)
с действительными коэффициентами. Суждение о знаках вещест-
венных частей корней характеристического уравнения (5.9)
может производиться и без решения самого характеристического
уравнения.
k
α
Возможны два принципиальных подхода к оценке положения
корней относительно мнимой оси комплексной плоскости.
10
Критерии устойчивости первого подхода (назовем их класси-
ческими) базируются на свойствах характеристического уравне-
ния. Критерии устойчивости второго подхода основаны на свой-
ствах самой матрицы
[
.
]
A
5.4. КРИТЕРИИ УСТОЙЧИВОСТИ, СВЯЗАННЫЕ
С ХАРАКТЕРИСТИЧЕСКИМ УРАВНЕНИЕМ
5.4.1. АЛГЕБРАИЧЕСКИЕ КРИТЕРИИ УСТОЙЧИВОСТИ
Они определяют систему неравенств для коэффициентов ха-
рактеристического уравнения.
Утверждение 5.6
У асимптотически устойчивого уравнения состояния все ко-
эффициенты его характеристического уравнения положительны.
Для доказательства представим характеристический полином
в виде произведения
n одночленов
)()()(
10 n
aD
λ
−
λ
λ
−
λ
=
λ K
, (5.10)
где его корни.
),,2,1( nj
j
K=λ
В асимптотической устойчивой системе они могут быть веще-
ственными отрицательными и комплексно-сопряженными с отри-
цательными вещественными частями. Например:
11
α−=λ
;
223,2
ω
±
α
−
=
λ
j
.
Для данных вещественных и комплексно-сопряженных кор-
ней соответствующие одночлены полинома (5.10) будут иметь
только положительные коэффициенты:
11
α
+
λ
=
λ
−
λ
;
.
2
2
2
2232
)()())(( ω+α+λ=ω+α+λ=λ−λλ−λ j
222
)( α+λω− j
Следовательно, характеристический полином, полученный в
результате перемножения одночленов с положительными коэффи-
циентами, будет иметь только положительные коэффициенты.
Это
условие является необходимым, но не достаточным для апериоди-
11
ческой устойчивости. (Если все корни - вещественные отрицатель-
ные (имеем апериодическую устойчивость), то полином имеет
только положительные коэффициенты).
Вместе с тем оно гаран-
тирует отсутствие положительных вещественных корней
(каж-
дый корень обращает полином (5.9) в нуль; положительное число
никогда не обратит в нуль полином вида (5.9) с положительными
коэффициентами).
Поэтому при положительности коэффициентов характеристи-
ческого уравнения неустойчивость (если она имеет место), будет
иметь всегда колебательный характер. Иными словами,
положи-
тельность коэффициентов характеристического полинома -
необходимое и достаточное условие отсутствия апериодической
неустойчивости ("сползания").
)(λD
Критерий Гурвица
Для устойчивости системы коэффициенты характеристиче-
ского полинома не только должны быть положительными, но и
удовлетворять определенным соотношениям. Эти соотношения,
называемые критерием Гурвица, задаются в виде неравенств, со-
блюдение которых является необходимым и достаточным условием
асимптотической устойчивости системы любого порядка.
Для формулирования этих неравенств строится квадратная
матрица Гурвица
n-го порядка из коэффициентов характеристиче-
ского уравнения.
На главной диагонали матрицы располагаются коэффициенты
полинома в порядке возрастания их индексов, начиная (вверху)
и заканчивая (внизу). В нечетных строках располагаются коэф-
фициенты с нечетными индексами, в четных строках - с четными
индексами (номера индексов возрастают слева направо). Все ос-
тальные элементы матрицы считаются нулевыми.
1
a
n
a
12
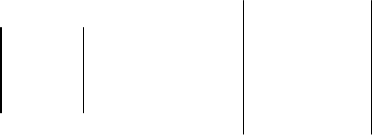
(5.11)
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
−−
−−
nnn
nn
aaa
aa
aaa
aaa
aaaa
aaaa
24
13
420
531
6420
7531
0000
00000
0000
0000
000
000
K
K
KKKKKKKK
K
K
K
K
Для асимптотической устойчивости системы необходимо и
достаточно, чтобы были положительными
n
иагональных мино-
ров (
n
определителей Гурвица) матрицы Гурвица:
д
;
0
11
>=Δ a
0
20
31
2
>=Δ
aa
aa
;
0
0
31
420
531
3
>=Δ
aa
aaa
aaa
; .(5.12)
0>Δ
n
K
Последний определитель связан простым выражением с предпо-
следним
1−
Δ
=
Δ
nnn
a
. (5.13)
Проанализируем критерии (5.12), (5.13) для систем с невысо-
кими порядками. Легко видеть, что для систем первого (
0
2
=
a
) и
второго порядка (
a
) условия
0
3
= 0
1
>
Δ
и
0
2
>
Δ
эквивалентны
положительности коэффициентов характеристических уравнений:
0
10
=
+λ aa
; .
0
21
2
0
=+λ+λ aaa
Следовательно, для этих систем
положительность коэффициен-
тов характеристического уравнения является необходимым и
достаточным условием их асимптотической устойчивости.
Для систем третьего порядка (
0
4
=
a
) с характеристическим
уравнением
0
32
2
1
3
0
=+λ+λ+λ aaaa
условия Гурвица ;
0
1
>Δ 0
2
>
Δ
;
0
3
>
Δ
сводятся к следующим:
1- к положительности коэффициентов
)3,,0( K
=
ja
j
,
13

2- выполнению неравенства
0
30212
>
−
=
Δ
aaaa
(произведение
средних коэффициентов уравнения должно быть больше произве-
дения крайних).
При невыполнении второго условия и при положительности коэф-
фициентов (в этом случае (
0
2
<
Δ
) из (5.13) следует, что и )
имеем колебательную неустойчивость ( два комплексно-
сопряженных корня являются правыми (вещественных правых кор-
ней нет, так как все коэффициенты положительны)).
0
3
<Δ
j
a
Для уравнения четвертого порядка (
0
5
=
a
)
0
43
2
2
3
1
4
0
=+λ+λ+λ+λ aaaaa
при положительности коэффициентов имеется лишь одно условие
устойчивости - положительность предпоследнего определителя
Гурвица (то же условие, что и в системе третьего порядка)
0)(
0
0
2
1430213
31
420
31
3
>−−==Δ aaaaaaa
aa
aaa
aa
.
Действительно, видим, что если
0
3
>
Δ
, то
и
0
30212
>−=Δ aaaa 0
434
>
Δ
=Δ a
.
Критерий Гурвица для систем небольшой размерности (не
выше третьей и четвертой степени) дает возможность аналитически
оценить влияние на устойчивость варьирования какого-либо пара-
метра при постоянстве остальных.
В заключение отметим еще раз условия асимптотической ус-
тойчивости:
-
0>
j
a
для систем первого и второго порядков;
-
0>
j
a
, предпоследний определитель Гурвица положителен
для систем третьего и четвертого порядка.
Оценим границы устойчивости.
Гурвиц показал, что если устойчивую систему приближать к
границе устойчивости, непрерывно изменяя коэффициенты харак-
теристического уравнения, то, прежде всего, станет равным нулю
14

последний определитель Гурвица
1−
Δ
=
Δ
nnn
a
. Очевидно возможны
два варианта выполнения этого условия:
1)
0=
n
a
,
0
1
>
. В этом случае из выражения для характеристи-
ческого полинома (5.9) видно, что при
0
Δ
−n
=
n
a
имеем нулевой ко-
рень (
0=λ
). Это граница апериодической устойчивости (один
действительный корень находится на мнимой оси). Система
«сползает» в неустойчивый режим. Для нее все определители
Гурвица положительны, кроме последнего (
0≤
Δ
n
).
2)
0
1
=Δ
−
,
0>
n
a
. На границе устойчивости имеем пару чисто
мнимых комплексно-сопряженных корней:
1
n
2,1
ω±=
λ
j
. Это гра-
ница колебательной устойчивости. При ее переходе начинается
самораскачивание системы с частотой
1
ω
.
Если и дальше изменять коэффициенты, уводя систему от ус-
тойчивости, то могут стать отрицательными и другие определители
Гурвица, а вновь может стать положительным.
1−
Δ
n
Для определения числа корней, появившихся в правой полу-
плоскости, удобно использовать число смены знаков у элементов
ряда
nnnnn
aa =
Δ
Δ
Δ
Δ
Δ
ΔΔ
−−− 1211210
,,,,, K
.
Очевидно у устойчивой системы все эти элементы положительны.
Рассмотрим последовательно возникающие ситуации:
1. При смене знака
n
a
(с положительного на отрицательный) и по-
ложительности всех определителей, кроме последнего (
n
Δ
меняет
знак с положительного на отрицательный), имеем только одну сме-
ну знака в ряду (у последнего элемента) и, следовательно, один
правый (вещественный) корень.
2. Если
n
a
станет снова положительным, а
0
1
<
Δ
−n
и поэтому
0<
, то имеем две смены знака в ряду у двух последних элемен-
тов и, следовательно, два правых корня.
Δ
n
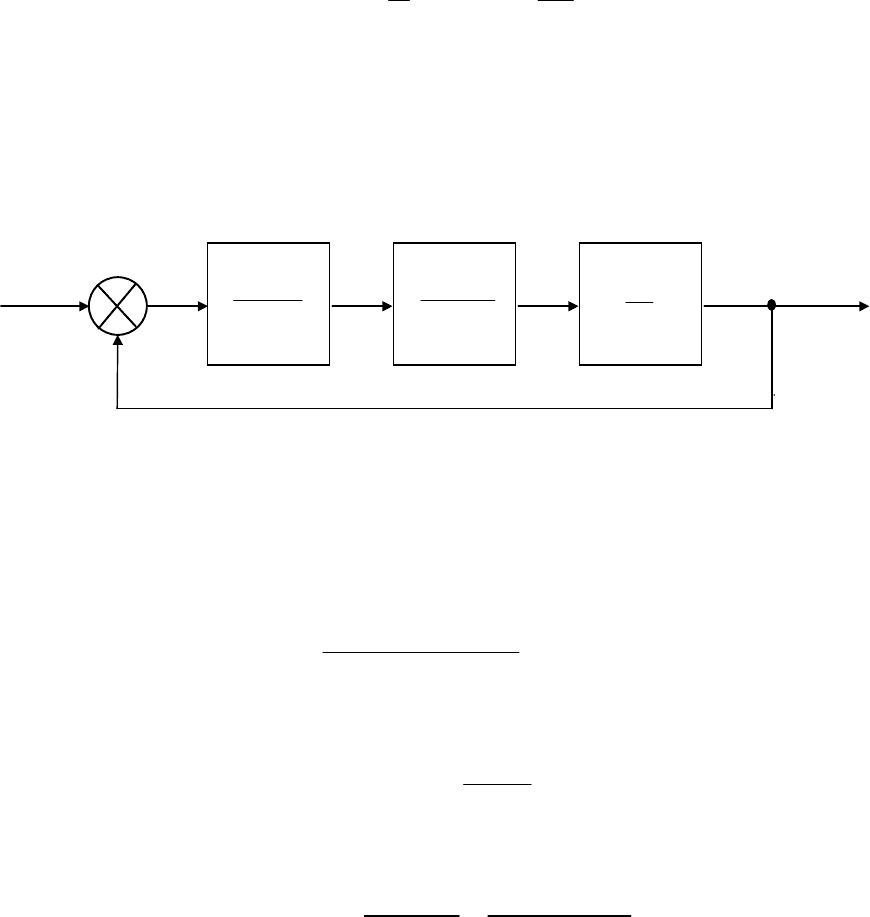
3. При
0
0
=a
(имеем смену знака у первого элемента ряда) грани-
ца устойчивости соответствует бесконечно большому корню. Дей-
ствительно, если уравнение (5.9) поделить на
n
λ
, то будем иметь:
15
0
11
10
=
λ
++
λ
+
n
n
aaa K
.
Отсюда видим, что при корнем уравнения является беско-
нечность .
0
0
=a
∞=λ
ПРИМЕР 5.1
g(t)
s
k
3
1
1
1
+sT
k
1
2
2
+sT
k
x
Рис. 5.5. Структурная схема с астатизмом
первого порядка
Для системы с астатизмом первого порядка имеем передаточную функцию
разомкнутой цепи
.,
)1)(1(
)(
321
21
kkkk
sTsTs
k
sW =
++
=
Обозначая
,
)(
)(
)(
sL
skN
sW =
получим для передаточной функции замкнутой системы:
)()(
)(
)(1
)(
)(
skNsL
skN
sW
sW
s
+
=
+
=Φ
.
Характеристическое уравнение замкнутой системы будет иметь вид
.0)()()()(
2
21
3
21
=++++=+= kssTTsTTskNsLsD
Для его устойчивости по Гурвицу:
).(,0
3021212130212
aaaaTkTTTaaaa >>
+
⇒>−=Δ
Границы устойчивости определяются из равенств
0
1
=Δ
=
Δ
−nnn
a
и
.
0
0
=a
Первая граница: имеем
0
3
=
Δ
=
Δ
n
. Принимаем
21
Δ=
Δ
−n
>0, тогда
.
0
3
=== kaa
n
16

Вторая граница: имеем
0
3
=
Δ
=
Δ
n
21
TTk
гр
. Принимаем >0, тогда
, отсюда
kaa
n
==
3
0
21
=Δ=Δ
−n
21
TT
=
+
. Следовательно,
21
11
TT
k
гр
+=
.
Третья граница: имеем
0
0
=
a
, тогда
0
21
=
TT
.
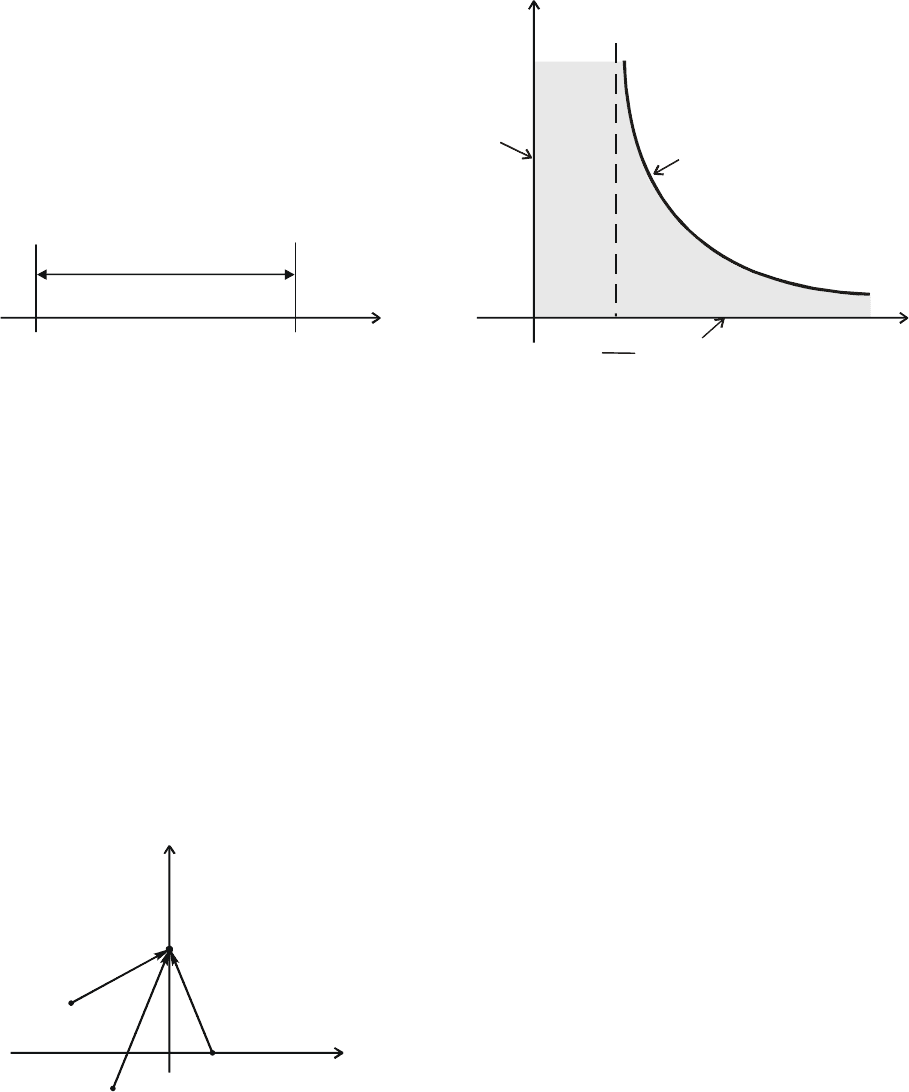
Область устойчивости по одному параметру – коэффициенту усиления k –
показана на рис. 5.6.
Границы устойчивости можно построить в плоскости двух параметров и
при T
2
=const (рис.5.7).
k
1
T
Первая граница совпадает с осью . Вторая граница следует из ра-
венства
)0( =k
1
T
.
1
,1)(
2
1
T
aakT ==−
Она представляет гиперболу с асимптотами
0
1
=
T
и . Третья граница
совпадает с осью .
0=k
)0(
1
=T
k
Видно, что при увеличении постоянных и область устойчивости
сужается. Из рис.5.6 и 5.7 также видно, что при фиксированных значениях и
существует граничное значение коэффициента усиления , при превышении
которого система становится неустойчивой. Наблюдается противоречие между тре-
бованием точности (увеличение ) и устойчивости (ограничение ).
1
T
2
T
k =
1
T
2
T
гр
k
k k
При или стремящихся к нулю имеем
1
T
2
T
∞
→
гр
k
.
Ввиду трудоемкости вычисления определителей Гурвица кри-
терий устойчивости Гурвица обычно применяют для систем с по-
рядками не выше пятого.
Для анализа устойчивости линейных систем высокого порядка
используют табличный критерий Рауса, имеющий алгоритмиче-
ский характер и меньший объем вычислений по сравнению с кри-
терием Гурвица [51].
17
0
k
гр
k
Область
устойчивости
I
II
III
0
k
1
T
2
Интервал
устойчивости
T
1
Рис. 5.6. Область (интервал)
устойчивости системы рис. 5.5 по
одному параметру - коэффициенту
усиления k
Рис. 5.7. Область устойчивости
системы рис. 5.5 по параметрам k и Т
(I, II, III - границы области)
1
5.4.2. ЧАСТОТНЫЕ КРИТЕРИИ УСТОЙЧИВОСТИ
Критерий Михайлова
Представим характеристический полином системы
n-го по-
рядка
n
n
apa +++
n
papD =
−
K
1
10
)(
()(
0
papD
в виде произведения одночленов
)())(
21 n
ppppp −
−
−
=
K
,
где
i
— корни полинома.
p
Будем полагать, что комплексное
число
ωα
j
p
+
=
находится на мнимой
оси
j
комплексной плоскости, т.е.
ω
j
p
=
.
Множитель
)ω(
i
pj
−
на ком-
плексной плоскости представляет со-
бой вектор с концом в точке
ω
j
(вектор, направленный от вычи-
таемого к уменьшаемому).
p
1
p
2
p
3
+1
j
ω
+
j
0
Рис. 5.8. К построению годографа
характеристического полинома
Комплексное число
18
)ω()ω()ω(
210
pjpjajD
−
−
=
K
(5.14)
имеет аргумент
. (5.15)
∑
=
=
n
i
i
pjjD
1
)-ω(arg)ω(arg
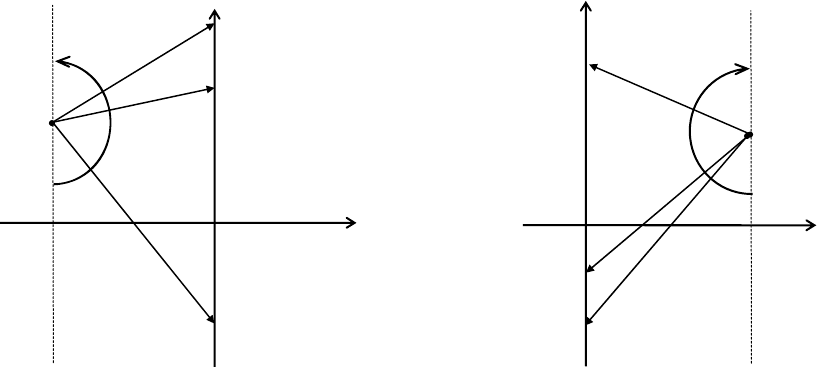
Примем вначале, что корень
p
i
принадлежит левой полуплос-
кости (рис.5.9 а). В этом случае вектор
)ω(
i
pj
−
при изменении
от –∞ до +∞ будет иметь приращение аргумента, равное радиан:
ω
π
∞
<
<
∞
−
=
Δ
ω
. π)-ω(arg
i
pjD
Если корень находится в правой полуплоскости, то, как
видно из рис. 5.9 б,
i
p
∞
<
<
∞
−
−
=
Δ
ω
. π)-ω(arg
i
pjD
+j
+j
ω
j
+1
+1
0
0
а
)
б
)
p
i
p
Рис. 5.9. Приращение аргумента характеристического полинома, вызывае-
мое левым (а) и правым (б) корнем
-π
π
Если все корни характеристического полинома (5.14) принад-
лежат левой полуплоскости, то согласно (5.15) имеем
∞<<∞−
=
Δ
ω
.π)ω(arg n
j
D
(5.16)
Если среди корней характеристического полинома корней
лежат в правой полуплоскости, а остальные
m
)( mn
−
- в левой полу-
19
