Афанасьев А.А. Математические основы теории систем управления
Подождите немного. Документ загружается.

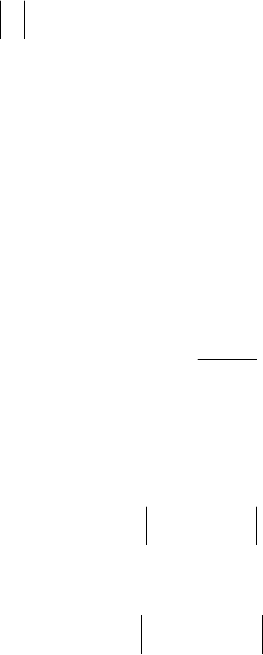
н ивости и др.) системы авто-ие, затухание за период, запас устойч
ческого регулирования [9].
5.7.1 ПОСТРОЕНИЕ КРИТЕРИАЛЬНОЙ МАТРИЦЫ
мати
[]
B
ДЛЯ ПОЛУПЛОСКОСТИ
0Re
<
σ
<
λ
Велич ина
σ
носит название степени устойчивости. Геомет-
рически он арактеризует расстояние от мнимой оси до ближай-
шего
а х
собственного числа (вещественного или комплексного) мат-
рицы (рис.5.41). Параметр
[]
A
σ
в ряде случаев характеризует бы-
строту затухания переходного процесса.
Найдем функцию, отображающую полуплоскость на
соответствии с форм ид
σ<λRe
внутренность единичного круга с центром в начале координат. В
улой (5.73) функция имеет в
σ+
−ρ
+
ρ
=λ
1
1
, (5.97)
т тся влево на величину
σ
. Под-
ставив
. е. граница полуплоскости сдвигае
(5.97) в характеристическое уравнение
[]
0
−
λ
=
EA
посл разований [52]:
, (5.98)
получим е ряда преоб
[]
0
1
=
ρ
−
EB
, (5.99)
где
[
]
[
]
(
)
1
1
2
−
σ−−+= EEAEB
. (5.100)
Для того чтобы собстве
[
]
A
нные числа матрицы находились
левее прямой
σ
<
λe
матрицы
[]
1
B
принадлежал
Матрица
R
обладает
необходимо и достаточно, спектр
внутренности круга.
спектром, если усло-
при
чтобы
единичного
выполняется
1
таким
вие
[]
1
→
k
B
[]
B
0
∞
→
k
.
70
5.7.2. ПОСТРОЕНИЕ КРИТЕРИАЛЬНЫХ МАТРИЦ
[]
B
ДЛЯ
ВЕРТИК ЬАЛ НОЙ ПОЛОСЫ
то спектр матрицы
[
]
A
Будем полагать, ч заключен внутри вер-
икальной полосы, задаваемой пересечен
т ием неравенств:
σ
<
λ
Re
, (5.101)
ξ
>
λ
Re
, (5.102)
причем
σ<ξ
(рис. 5.4
Знание собственного числа матрицы с
5).
наибольшей по модулю
ещественной частью позволяет более
оранту кривой переходного процесса. Например, известно, что
сли
в точно оценить мажоранту и
мин
108 ÷>σξ
е , то дальнейшее увеличение
и не меняет верхнюю ограничительную кри
круг, будем исхо е извес
робно - линейное преобразование (5.97) переводит полу-
этого отношения поч-
т вую переходного про-
цесса - мажоранту [52].
При поиске функции, отображающей полосу на единичный
дить из уж тных зависимостей.
Д
плоскость (5.101) во внутренность единичного круга в корневом
пространстве матрицы
[
]
.
1
B
Преобразование
ξ+
⎟
⎟
⎠
⎜
⎜
⎝
−ρ
−=λ
1
(5.103)
еводит полуплоскость (5.102) (п
⎞⎛
+ρ
1
пер олуплоскость справа от прямой
) во внутренность
ст
е подстановки
ие (5.98) определим
[52]
ξ=λRe
про н
единичного круга в корневом
стра ве новой матрицы
[]
2
B
. Посл
(5.103) в характеристическое
уравнен
[
]
0
2
=
ρ
−
E
(5.104)
где
B
,
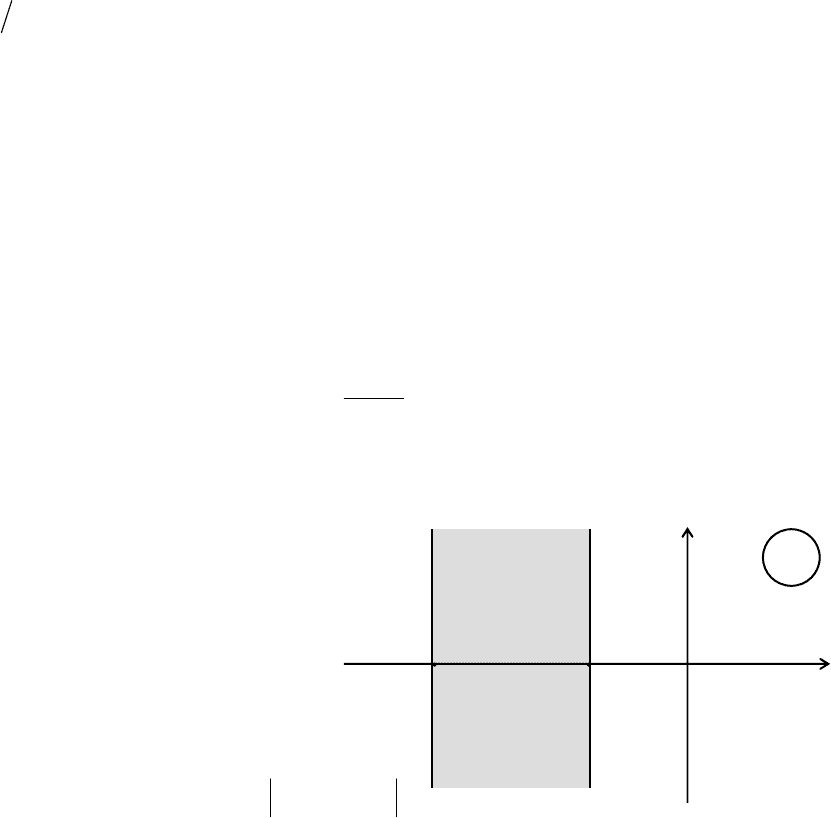
+j
λ
0
σ
ξ
+1
Рис. 5.45. Локализация спектра матрицы [A]
внутри вертикальной бесконечной полосы
71

[
]
[
]
(
)
1
2
2
−
ξ−+−= EEAEB
. (5.105)
Преобразование (5.103) получено путем разворота границы
полуплоскости на угол 180
о
(это равносильно умножению функции
()()
11 −ρ+ρ=λ
на число
1
2
−=j
) и сдви ее влево на величину
0<ξ
.
Пересечение
гу
полуплоскостей (5.101) (5.102) задает вертикаль-
ую полосу.
Пересечение единичных кругов
и совпадает самим этим еди
Таким образом, для того чтобы
л в о лосе
н
корневых плоскостей матриц
[
ничным кругом.
]
1
B
[]
2
B
собственные числа матрицы
[
ежали в ертикальн й по
]
A
Re
<
ξ
необходимо и достаточно, чт
[]
1
B
и
[]
B
лежали внутри ед
оорд
σ
<
λ
,
обы все собственные числа матриц
иничного круга с центром в начале
обходимого и достаточного условия
при
2
к инат.
При выполнении этого не
имеем
[]
0
1
→
k
B
и
[
B
]
0
2
→
k
∞
→
k
.
ТЕРИАЛЬНЫХ МАТРИЦ
ПОЛУПОЛОСЫ
[]
B
5.7.3. ПОСТРОЕНИЕ КРИ
ДЛЯ ГОРИЗОНТАЛЬНОЙ
При жестких ограничениях на величину колебательности сис-
темы спектр собственных чисел матрицы
[
]
A
локализуют в сравни-
тельно узкой полуполосе (рис. 5.46), задаваемой пересечением трех
полуплоскостей:
α
<
λ
Re
, (5.106)
β
<
λ
Jm
, (5.107)
β
−
>
λ
Jm
. (5.108)
Найдем функции, отображающие указанные полуплоскости на
внутренность круга с центром в начале координат.
72

Как известно, дробно-линейное преобразование (5.73) ото-
ражает левую половину комплексной
ренность единичного круга с центром в начале ком-
б полуплоскости
λ
во внут-
координат
плексной плоскости
ρ
.
Если умножим правую часть формулы (5.73) на
j
, то это рав-
носильно повороту вертикальной прямой (границы левой полу-
плоскости) на угол
2π
. Функция
1
1
−ρ
+
ρ
=λ j
будет отображать нижнюю половину плоскости на единичный
руг.
Если границу этой полу-
λ
к
плоскости (линию
0Im
=
λ
)
сдвин вверх на величину
β
ем
j
, то функция
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
β+
−ρ
+ρ
=λ
1
1
j
(5.109)
+j
λ
2β
+1
0
α
будет отображать смещенную
вверх (на величину
β
j
) ниж-
полуплоскость на внут-
ость единичного круга с
ентром в начале координат.
Подставим выражение (5.109) в характеристическое уравне-
ие (
Рис. 5.46. Локализация спектра матрицы [A]
внут
полуполосы
ри горизонтальной бесконечной
нюю
ренн
ц
н 5.98), которое после ряда преобразований можно привести к
виду
[
]
0
3
=
ρ
−
EB
, (5.110)
где
[]
[
]
(
)
1−
β+ EEAj
3
Аналогично верхняя полуплоскость, смещенная вниз на вели-
чину
β
2 +−= EB
. (5.111)
j
, может быть отображена на круг единичного радиуса с
центром в начале координат с помощью функции
73

⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
β+
−ρ
+ρ
−=λ
1
1
j
. (5.112)
Подставив (5.112) в (5.98), получим:
[]
0
4
=
ρ
−
EB
, (5.113)
где
[]
[
]
(
)
1−
β−− EE
4
2+= AjEB
Полученн матрица
[]
4
B
явл
по отношению к матрице
[]
3
B
. След
этих матриц комплексно- сопряжен
(наприм
. (5.114)
ая яется комплексно- сопряженной
овательно, и собственные числа
ы. Поэтому одну этих матриц
ер, ) можно из рассмотрения при локализа-
ции спектра риц
обы спектр матрицы при-
неравенствами (5.106)- (5.108),
ния следующих двух условий:
и при
из
[]
4
B
мат
исключить
[]
A
. ы
[]
A
Таким образом, для того чт
надлежал полуполосе, задаваемой
необходимо и достаточно выполне
[]
B 0→
k
1 3
[]
0→
k
B
∞
→
k
.
таточно узкой, то в исследуемой
цесс, близкий к апериодическо-
Я ОБЛАСТИ,
ИМЕЮЩЕЙ ФОРМУ ТРАПЕЦИИ
Если выбрать полуполосу дос
системе получим переходный про
му.
5.7.4. ПОСТРОЕНИЕ КРИТЕРИАЛЬНЫХ МАТРИЦ ДЛ
Отношение мнимой части
β
(угловой частоты колебаний) к
вещественной
α
(коэффициенту затухания) собственного числа
матрицы называется колебательностью
α
β
=μ
.
Целесообразно ограничивать колебательность, т.к. это приво-
дит к увеличению затухания колебания за период.
74
Задание определенной колебательности эквивалентно распо-
ожению спектра исходной матрицы
[
]
A
проведенными
л в области, образованной
двумя симметричными лучами, из начала координат
од уп глом
ϕ
к вещественной оси (рис.5.47). Причем
μ
=
ϕ
t
g
.
Трапецеидальная фигура на
5.47 может рассматриваться
область пересечения четырех
олуплоскостей.
Область в виде вертикальной
полосы (рис.5.45) ранее была
представлена двумя критериаль-
ными матрицами
2
рис.
как
п
[]
1
B
и
[
]
B
2
(см.
формулы (5.100) и (5.105)).
Найдем теперь функцию,
отображающую полуплоскость с
верхней границей в виде прямой с
точками 1 и 2. Выражение для нее
получим из формулы (5.73), уве-
личив аргумент ее правой части
на угол
()
ϕ
−
π 2
:
⎟
⎠
⎞
⎜
⎛
−
π
+ρ
=λ
1
j
⎝
ϕ
−ρ
2
1
e
.
сле подстановки (5.115) в характеристическое уравнение
.98) можем найти
(5.115)
По
(5
[
]
0
5
=
ρ
−
EB
, )
где
(5.116
[] []
(
)
1
5
2
−
ϕj
−−+= EeAjEB
. (5.117)
Критериальная матрица
[
]
6
B
для полуплоскости с нижней
прямолинейной границей, через точки 3 и 4 (рис.5.47),
будет комплексно сопряжена матрицей
проходящей
с
[
]
5
B
. Поэтому матрицу
можно исключить из .
[]
6
B
рассмотрения
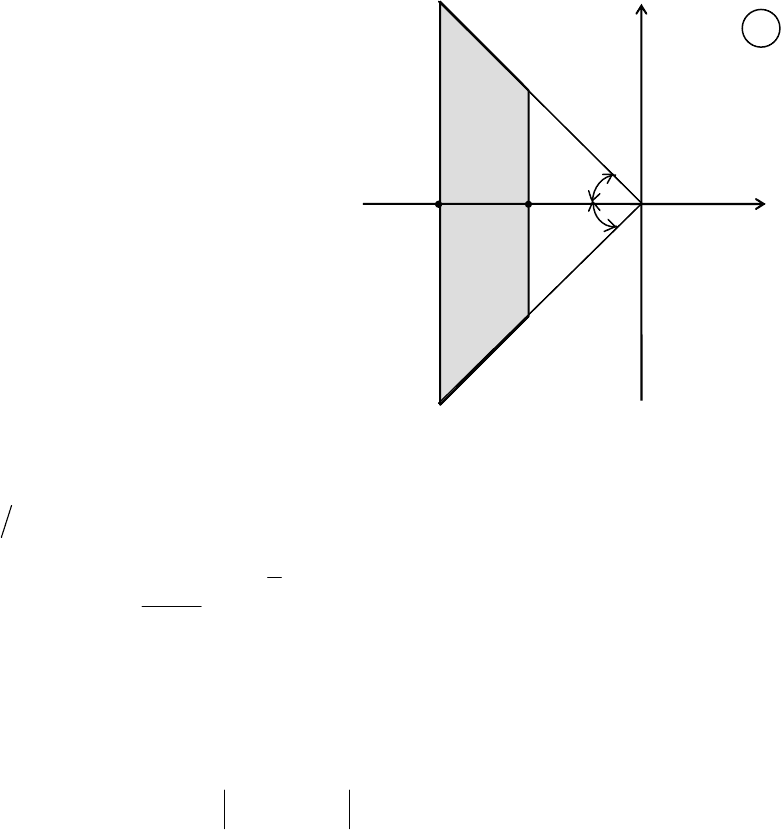
σ
ϕ
+j
λ
1
0
ξ
3
ϕ
+1
4
Рис. 5.47. Локализация спектра матри-
цы внутри области, имеющей форму
трапеции
75

76
Критерий формир зом. уется следующим обра
[
]
A
й
Для того чтобы спектр исходной матрицы принадлежал
заданной трапеции в левой половине корневой комплексной плоско-
мо и достаточно выполнение условисти , необходи :
λ
[] []
[
]
;0;0;0
521
→→→ BBB
при
kkk
∞
→
k
. (5.118
евая сторона трапеции, задаваемая прямой
)
Если л
ξ
=λRe
,
отодвигается влево до бесконечности, то второй предел в условиях
(5
Если вместо трапеции за-
(5.118) исключаются
.118) снимается.
дается область, ограниченная
двумя лучами (рис.5.48), то из
+j
λ
+1
0
ϕ
ϕ
условий
первых два.
Рис. 5.4
внут и,
8. Локализация спектра матрицы
ри област ограниченной двумя
лучами
ГЛАВА ШЕСТА
НИЯ
6.1. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ
УРАВНЕНИЙ СПЕЦИАЛЬНОГО ВИДА
6.1.1. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ ПЕРИОДИЧЕСКИХ СИСТЕМ
Я
УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ НЕСТАЦИОНАРНЫХ
УРАВНЕНИЙ СОСТОЯ
НЕСТАЦИОНАРНЫХ
Из структуры решений линейных систем с периодической
матрицей
(
)
[]
tA
, рассмотренных в главе 3, следуют выво б их
устойчивости:
ды о
1) Линейная однородная п дичес
ной матрицей уст только тогда, когда все
ее мультипликаторы
ерио кая система с непрерыв-
()
[]
tA
ойчива тогда и
j
ρ
расположены или на границе еди- внутри
(
)
1≤ρ
j
. ничного круга
2) Для асимпто одимо и достаточ-
но, чтобы все мульти ь внутри единичного
тической системы необх
пликаторы ее находилис
(
)
1<ρ
j
. круга
6.1.2. УСТОЙЧИВОСТЬ ЛИНЕЙНОЙ СИСТЕМЫ С ПОЧТИ
ПОС
ых приведено
6.1
ТОЯННОЙ МАТРИЦЕЙ
Рассмотрим две теоремы, доказательство котор
в
[]
16
.
Теорема
Пусть система
[]
xA
d
t
xd
=
, (6.1)
ва ригде
[]
A
постоянная матрица размерности n, устойчи п
∞
→
t
.
Тогда система
77

[]
()
[]
{}
ytBA
d
t
yd
+=
, (6.2)
определена на интервале
()
[]
tB
[
)
∞
,
0
t
где матрица и интегрально
ограничена по норме:
()
[]
∞<
∫
B
t
0
, 6.3)
такж
∞
dtt
(
е устойчива при
∞→
t
.
Теорема 6.2
Если систе при
∞→
t
ма (6.1) асимптотически устойчива , то
система (6.2) также асимптотически устойчива, если
()
[]
0→tB
при
∞
→
t
. (6.4)
Замечание
верной, ес
6.1
Теорема 6.2 остается ли
(
)
[
]
ktB
<
при
T
t
≥
, где
положительное
число
k
достаточно . мало
Следствие теоремы 6.2
линомиальными коэффициентами Линейная система с по
[] [] []
{}
yAtAtA
dt
m
mm
+++=
−
K
1
10
, (6.5)
[]
),,1,0( mkA =
yd
где
k
K
- постоянные матрицы размера n, асим-
птотически устойчива, если все собственные числа
),,1( nj K=
j
λ
матрицы
0
A
имеют отрицательные вещественные части
[]
(
)
0Re <
j
λ
.
Действительно, полагая
()
[]
τττ
t
m
=
+
,
1
1
ddttmt
m
m
m
=+=
+
+
,1
1
1
,
части (6.5) на
m
t
будем иметь, разделив левую и правую
78

[]
()
[]
{}
yBA
d
τ
yd
τ
+=
0
,
где
[
]
[
]
()
[]
()
[]
()
[]
11
11
++
++
mm
mm
ττ
Так как
1
1
++=
m
m
B
τ
K
.
A
A
()
[
]
0→
τ
B
при
∞
→
t
при
∞
→
τ
, причем
∞→
τ
, то
рассм емы
6.2.
ВА
Решения линейной однородной системы
атриваемое следствие непосредственно вытекает из теор
6.2. ПОКАЗАТЕЛИ ЛЯПУНО
()
[]
xtA
dt
xd
=
(6.6)
на временном интервале
∞
<
<
tt
могут рассматриваться как
0
функции
(
)
jtxx
jj
, n,,2,1 K
=
=
с тремя типами поведения:
1.
Ограниченные функции, модул
меньше некоторой положительной .
2.
Убывающие функции, модуль которых при
ь которых при
tt >
, всегда
величины
0
∞→
t
стремится к
нулю.
3.
Неограниченные функции, модуль которых при
∞→
t
стрем
е модуля комплекснознач
ит-
ся к бесконечности.
Ляпунов предложил изменени ной (в
общем случае) функции
(
)
(
)
(
)
txjtxtx ImRe
+
=
сравнивать с показательной функцией
t
e
α
, (6.7)
79
