Афанасьев А.А. Математические основы теории систем управления
Подождите немного. Документ загружается.

чивости неприменимы алгебраические критерии устойчивости.
Частотные критерии Михайлова и Найквиста для систем с запазды-
ванием сохраняют все свои формулировки.
При практическом исследовании устойчивости более удобен
критерий Найквиста. Рассмотрим некоторые особенности систем с
запаздыванием, пользуясь критерием Найквиста.
Из выражения для амплитудно-фазовой характеристики ра-
зомкнутой системы
τω
0τ
)ω()ω(
j
ejWjW
−
=
(5.37)
следует, что наличие запаздывания не меняет амплитудную час-
тотную характеристику:
)ω()ω(
0
AA
=
,
но существенно влияет на фазовую частотную характеристику:
τω)ω()ω(
0
−
ϕ
=
ϕ
,
причем
−∞=
ϕ
∞→
)ω(lim
ω
.
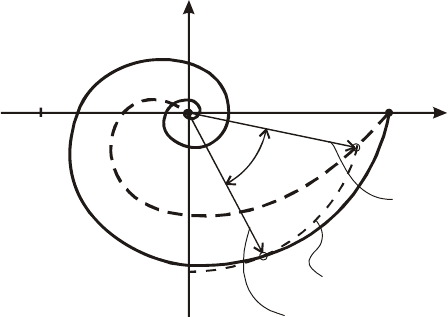
Вектор
)ω(
j
W
дополни-
тельно поворачивается отно-
сительно вектора в
отрицательном направлении
на угол . Этот угол с рос-
том возрастает. Поэтому
годограф вектор
)ω(
)ω(
0
jW
τω
ω
а
j
W
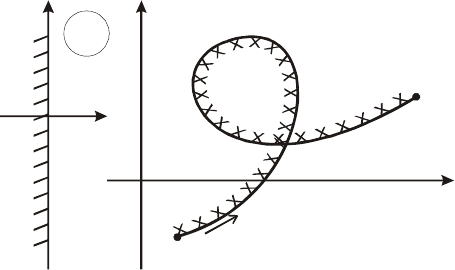
имеет спиральную форму, за-
кручиваясь у начала коорди-
нат (рис.5.29).
граф
1).
В
ая за
Пусть система без за-
паздывания устойчива и в разомкнутом и замкнутом состояниях.
Это значит, что частотный годо
)ω(
0
j
не охватывает точку
W
(-
ведем звено запаздывания и будем увеличивать запаздыва-
ние
τ
, наблюд деформацией годографа
)ω(
0
jW
. При некото-
ром значении
пр
ττ =
годограф пройдет через точку (-1) и, следова-
40
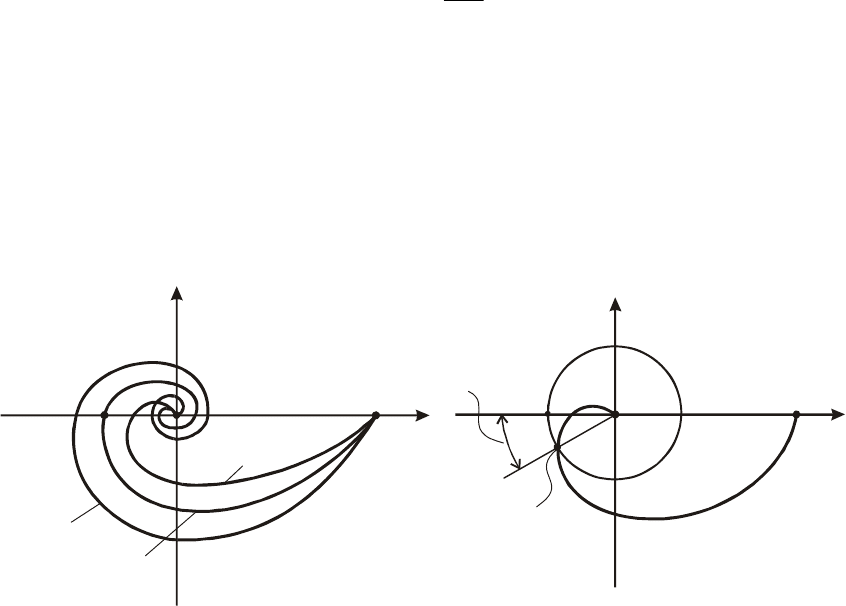
тельно, система окажется на границе устойчивости (рис.5.30). При
пр
ττ <
система устойчива, при
пр
ττ >
– неустойчива.
Значение предельного запаздывания
пр
τ
легко может быть
найдено графически. Для этого провед ужность единичного
радиус
ем
а с центром в начале плоскости, ко-
в точке с частотой
).
Предельное время запазд
окр
комплекснойкоординат
ывания
торая пересечет частотный годограф
)ω(
0
jW
c
ωω =
среза (
составит
c
пр
ω
γ
τ =
. (5.38)
В тех случаях, когда звено запаздывания находится в цепи ме-
стной обратной связи (его нет в прямой цепи), его влияние будет
другим. В зависимости от структуры системы это влияние может
системы
чтобы
быть
по
Зап
благоприятным, т.е. может улучшать устойчивость
аналогии с инерционной обратной связью.
ω=0
асы устойчивости, вводимые на основе критерия Найкви-
ста
Система автоматического регулирования не должна находить-
ся на границе устойчивости. Она должна обладать некоторым запа-
сом устойчивости, с тем, возможные вариации параметров
не нарушили ее устойчивость и не ухудшили качественные показа-
тели.
+j
+1
0
-1
ω=∞
τ=τ
пр
пр
τ=0
+j
+1
τ>τ
0-1
ω=∞
Wj
0
()
ω
γ
=
τω
пр c
=ω
c
ω=0
ω
Рис. 5.30. Деформация годографа Wj
при увеличении в звене запаздывания
()
ω
τ
времени запаздывания
τ
пр
Рис. 5.31. К определению предельного
41
Частотный критерий Найквис воляет оценить запас ус-
той
та поз
чивости системы по виду частотной характеристики ее разомк-
нутой цепи. Запасы устойчивости характеризуют удаление частот-
ного годографа разомкнутой цепи
)ω(
j
W
от критической точки (-
1).
На практике используют два запаса устойчивости: запас по
фазе и запас по амплитуде (по коэффициенту усиления).Они могут
ки,находиться либо с помощью годографа частотной характеристи
либо с помощью логарифмических амплитудно-фазовых частотных
характеристик.
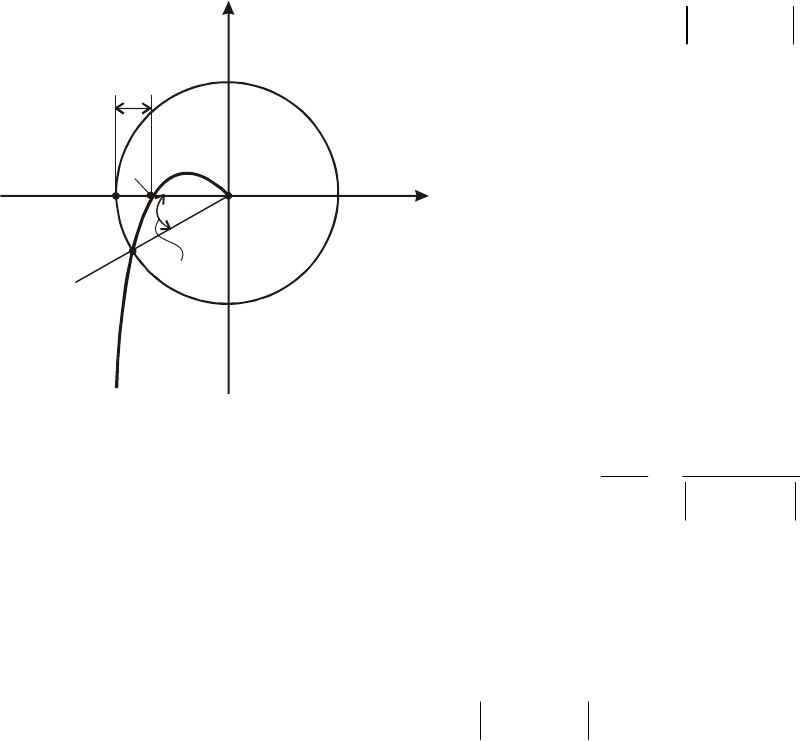
Запас устойчивости по фазе представляет собой угол
c
γ
(рис.5.32) между отрицательной полуосью и лучом, проходящим
через точку пересечения годографа
)ω(
j
W
Этой
с единичной окружно
. точке соответствует
амплитуда частотной характеристики
-
час-
стью с центром в начале координат
тота среза , для которой
равна единице
c
ω
+j
+1
0
-1
Δϕ=γ
c
ω=∞
Δ
A
ω
π
1)ω()ω(
cc
=
=
jWjA
.
Запас устойчивости по фазе
обеспечивает сохранение устой-
туде может характеризовать-
ся отрезком
чивости системы при увеличе-
нии запаздывания в прямой цепи
системы.
Запас устойчивости по ам-
пли
A
Δ
(рис.5.32). Чаще
оценивают этот запас отношени-
ем
,1
)(
π
jWk
показывающим, во сколь
1
ω
==β
k
пр
>
ко раз может быть увеличен коэффициент
усиления системы
k
Рис. 5.32. К определению запаса
устойчивости замкнутой системы
по фазе и амплитуде
при сохранении ее устойчивост
Запас устойчивости по амплитуде можно выразить в лога-
рифмическом масштабе
и.
)ω()ω(lg20βlg20
ππ
LjWL
зап
−
=
−==
.
42

Запасы устойчивости (рис. 5.33) показаны в виде соответст-
вующих отрезков, имеющих положительный знак для устойчивой и
отрицательный – для неустойчивой системы.
Численные значения запасов устойчивости выбирают исходя
из требований, предъявляемых к переходным процессам.
Выделение облас-
тей устойчивости
– способ Д-
разбиений
Коэффициен-
ты характеристиче-
ского уравнения
системы автомати-
ческого регулиро-
вания являются
функциями пара-
метров всех звень-
ев, входящих в
прямые и обратные
цепи. Некоторые
параметры (коэф-
фициенты усиле-
ния, постоянные
времени, времена
запаздывания) мо-
гут в процессе конструирования и настройки системы изменяться в
определенных пределах с целью обеспечения необходимых рабо-
чих показателей (точности, качества регулирования и др.). В этом
случае необходимо оценить возможные диапазоны варьирования
параметров системы, не вызывающих нарушения ее устойчивости.
Например, при варьировании какого-либо параметра можем
умозрительно предположить, что существуют интервалы значений
Π
L
зап
< 0
1
L, дБ
L
зап
> 0
1
2
1
ω
c2
γ
c
> 0
ϕ,
рад
ω
,c
-1
ω
,c
-1
γ
c
< 0
-/2
π
-
π
ω
π
ω
π
ω
c1
-3 /2
π
Рис. 5.33. Определение запаса устойчивости системы по
амплитуде и фазе с помощью логарифмических
амплитудных и фазовых частотных характеристик
43

Π
, при которых характеристический полином имеет только левые
корни. Эти интервалы на рис.5.34 отмечены жирными отрезками.
Аналогично для двух, трех и большого числа варьируемых
параметров, можно представить плоские и объемные области, для
которых система регулирования устойчива.
Сформируем задачу нахождения области устойчивости в про-
странстве параметров. Обозначим через – число правых корней
характеристического полинома степени , тогда
m
n mn
−
– число ле-
вых корней этого полинома (в предположении, что корней на мни-
мой оси нет).
В пространстве
параметров
можем
выявить некоторые
области ,
которым соответствуют правых и
),,2,1( ki K=
,(mD
i
Π
)mn −
m mn
−
левых корней полинома
. Например, если характеристический полином имеет
третью степень , то возможно существование в пространстве
параметров следующих четырех D – областей с конкретными зна-
чениями левых и правых корней:
),,1,0 nK=
0
П
Рис. 5.34. Интервалы значений параметра П, для
которых все корни характеристического полинома
являются левыми
(m
)3( =n
)0,3(),1,2(),2,1(),3,0( DDDD
,
из которых только первая является областью устойчивости.
Значениям параметров на границах D – областей соответст-
вуют корни характеристического уравнения (один или несколько),
лежащие на мнимой оси (
ω
λ
j
=
). Для этих корней, очевидно, спра-
ведливо
0)ω(
=
j
D
,
где – характеристический полином.
n
nn
aaaD ++λ+λ=λ
−
L
1
10
)(
Будем считать, что искомые параметры входят в состав коэф-
фициентов характеристического уравнения линейно, т.е. в характе-
ристическом уравнении они представлены только первой степенью
и отсутствуют их произведения. В этом случае характеристическое
уравнение имеет вид
)λ()λ()λ()λ(
110 kk
DDDD
Π
+
+
Π+
=
K
,
44

где – известные полиномы (в общем случае,
возможно, все n-й степени).
)λ(,),λ( ),λ(
10 k
DDD K
Ставится задача нахождения всех значений параметров
, при которых замкнутая система устойчива.
),,2,1( kj
j
K=Π
В зависимости от числа искомых параметров рассматривае-
мый метод называется методом D разбиения по
k
параметрам.
Чаще всего число
k
принимает значения 1,2 или 3.
D-разбиение по двум параметрам
Рассмотрим наиболее часто встречающийся на практике слу-
чай, когда два параметра
1
Π
и
2
Π
входят в характеристическое
уравнение линейно
0)λ()λ()λ()λ(
22110
=
Π
+
Π
+
= DDDD
. (5.39)
Найдем значения и
1
Π
2
Π
, при которых характеристическое урав-
нение (5.39) имеет пару чисто мнимых корней
i
jωλ
±
=
. (5.40)
После подстановки (5.40) в (5.39) получим уравнение
0)ω()ω()ω()ω(
i22i11i0i
=
Π
+
Π
+
= jDjDjDjD
. (5.41)
Входящие в него комплексы можно представить вещественными и
мнимыми слагаемыми
).ω()ω()ω(
),ω()ω()ω(
),ω()ω()ω(
i2i2i2
i1i1i1
i0i0i0
jjYjXjD
jjYjXjD
jjYjXjD
+=
+=
+
=
Тогда уравнение (5.41) распадается на два
, (5.42)
⎭
⎬
⎫
−=Π+Π
−=Π+Π
),ω()ω()ω(
),ω()ω()ω(
i0i22i11
i0i22i11
YYY
XXX
решая которые по формулам Крамера получим
,
Δ
Δ
,
Δ
Δ
2
2
1
1
=Π=Π
(5.43)
где
45

,
)ω()(ω
)ω()(ω
Δ
21
21
ii
ii
YY
XX
=
(5.44)
.
)ω()(ω
)ω()(ω
Δ;
)ω()(ω
)ω()(ω
Δ
01
01
2
20
20
1
ii
ii
ii
ii
YY
XX
YY
XX
−=−=
(5.45)
Для конкретного значения из формул (5.43) можем найти
соответствующие значения и
i
ω
1
Π
2
Π
.
Формулы (5.43) при изменении от 0 до +
∞ определяют
кривую D – разбиения на плоскости двух параметров
i
ω
1
Π
и .
2
Π
При изменении от -∞ до 0 кривая D – разбиения вторично
проходит те же самые точки, т.е. прочерчивается еще раз. Следова-
тельно, для нахождения этой кривой достаточно варьировать от
0 до +
∞.
i
ω
i
ω
Кривая D – разбиения в плоскости параметров
1
Π
и явля-
ется образом мнимой оси комплексной плоскости корней характе-
ристического полинома.
2
Π
Можно показать [18], что значения
1
Π
и
2
Π
, рассматривае-
мые по способу нахождения как функции частоты , обладают
свойством четности
ω
)ω()ω();ω()ω(
2211
−
Π
=
Π
−Π=Π
,
а определители и , наоборот, являются нечетными функ-
циями частоты . Четными являются также функции и .
Нечетными – и .
1
ΔΔ,
ω
2
Y,
2
Δ
0
21
X,X
0
X
1
Y Y
Особые прямые
При изменении определители (5.44), (5.45) непрерывно из-
меняются. При некоторых частотах
ω
i
ωω
=
может возникнуть си-
туация, когда все определители обратятся в нуль. Из формул для
определителей (5.44), (5.45) следует возможность такого варианта
при пропорциональности чисел:
)ω(
)ω(
)ω(
)ω(
)ω(
)ω(
0
0
2
2
1
1
i
i
i
i
i
i
Y
X
Y
X
Y
X
==
.
46
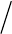
В этом случае одно уравнение в (5.42) является следствием друго-
го, т.е. эти уравнения линейно зависимы, следовательно, вместо
двух уравнений (5.42) нужно рассматривать одно, например пер-
вое:
)ω()ω()ω(
02211 iii
XXX
−
=
Π
+
Π
. (5.46)
Это уравнение определяет в плоскости параметров и
1
Π
2
Π
для
фиксированной частоты
i
ωω
=
прямую линию, называемую особой
прямой.
Чтобы выявить особые прямые, необходимо фиксировать все
значения , при которых определители одновременно
обращаются в нуль.
ω
21
ΔΔΔ, и
Если коэффициенты характеристического уравнения и
зависят от параметров
n
a
0
a
1
Π
и
2
Π
(
a
3n2211 nnn
aaa
+
Π+Π
=
;
), то в число частот следует включить
соответственно и
032021010
aaaa +Π+Π=
0ω =
i
i
ω
∞
=
i
ω
.
Поскольку функции и нечетные, то очевидно
21
Y,Y
0
Y
0)0()0(Y(0)Y
021
=
=
=
Y
.
Четность функций не требует их обязательного
обращения в 0 при . Поэтому уравнение (5.46) может быть
особой прямой и при
021
XX,X и
0
0
ω =
ω
=
i
.
Если для полинома
)
λ
(D
вместо
λ
взять величину обратную
(
λ1
), то условие будет соответствовать особой прямой (ес-
ли зависит от и ) при значении
0
0
=a
1
Π Π
0
a
2
∞
=
ω
.
Таким образом, для получения особых прямых нужно:
1)
принять равным нулю свободный член
n
a
характеристическо-
го полинома
)
λ
(D
, если он зависит от параметров
1
Π
и
2
Π
.
Получаем особую прямую для частоты
0ω
=
:
0
32211
=
+
Π
+
Π
=
nnnn
aaaa
;
2)
принять равным нулю коэффициент
0
a
полинома (в слагае-
мом с наивысшей степенью), если он также зависит от пара-
метров
1
Π
и
2
Π
. Получаем особую прямую для частоты
∞=ω
:
47
0
03
=+
202010 1
Π
+
Π
=
a
;
aaa
обращаются в оп-
ределители
3)
найти частоты
i
ω
, при
которых одновременно
нуль
0
2
ΔΔΔ
1
=
=
=
. Каждой
ая.
я D
из этих частот
i
ω
со-
ответствует особая
прям
Штриховка границ D – раз-
биений
Как уже отмечалось,
крива – разбиения в плоскости параметров
1
Π
и
Π
является
образом мнимой оси комплексной пл -
ческого полинома.
Нанесем на мнимую ось
2
оскости корней характеристи
штриховку слева, помня, что левая
системы.
, то будем штриховать левую сторону D – по от-
ы. Поэтому ее штрихов-
полуплоскость является областью устойчивости
Будем перемещаться вдоль D – кривой, увеличивая
ω
от - ∞ в
положительном направлении. Если при таком движении определи-
тель
0Δ >
кривой
ношению к направлению перемещения [18]. При изменении
ω
от -
∞ до + ∞ D – кривая будет пройдена дважд
ка будет двойной (рис.5.35.б).
Особая прямая, соответствующая частоте
∞
<
<
i
ω0
, снабжа-
ется двойной штриховкой, причем сторона штриховки меняется
пр о-
в
ересекает D – кривую (таких то-
ч
а
шт D -
мой особой прямой обращены навстречу друг другу.
Если на частоте в рассматриваемой точке определитель
только принимает нулевые значение, не меняя знака, то эта особая
прямая не штрихуется (рис.5.37).
только в одной точке ямой, для которой соблюдаются два усл
ия:
1)
в этой точке особая прямая п
ек может быть несколько, (рис.5.36)),
2)
в ней определитель меняет зн к.
В окрестности этой точки риховки – кривой и рассматривае
Δ
i
ω
Δ
0
0
П
1
П
2
а
ω=+∞
) б)
Δ
>0
ω=−∞
j
ω
α
ω=
0
λ
Рис. 5.35. Мнимая ось комплексной плоскости
арактеристического полинома (а) и ее обра
плоскости двух параметров – D – кривая (б
х з
на )
48
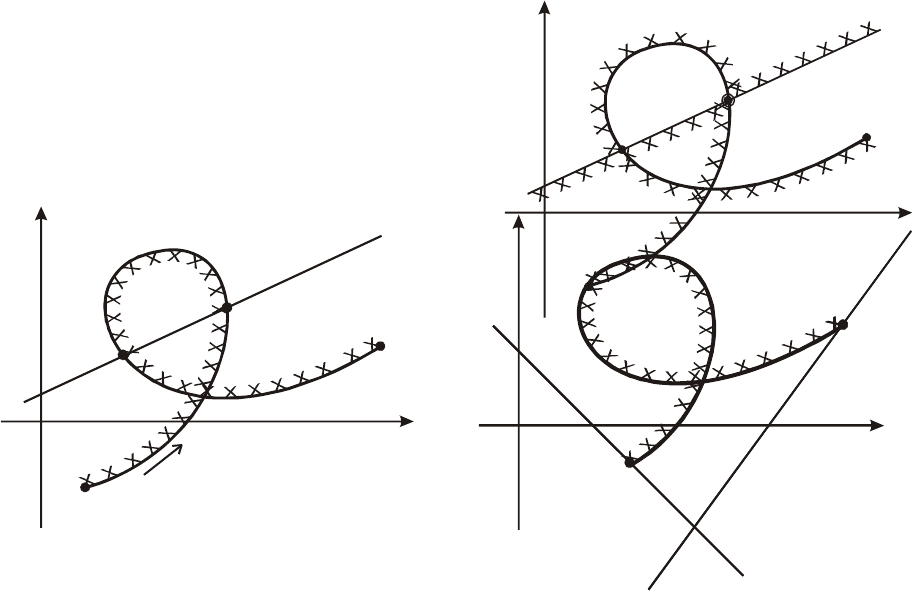
Особые прямые, соответствующие частотам
0ω =
и
∞
=
ω
,
снабжаются одинарной штриховкой. Выбор стороны штриховки
производится аналогично предыдущей особой прямой (рис.5.38).
Если известно распределе орней в одной из областей D –
разбиения, то, пользуясь изложенными выше п лами штрихов-
ки границ, легко найти распреде-
ление корней в других областях.
На рис. 5.36
÷5.38 через
)(mD
обозначим области, для ко-
торых число правых корней равно
ние к
рави
ивости. Определив для
и значения параметров
и подставив их в характеристическ
известными критериями устойчивости
и будет неустойчива.
е
Запишем характеристическое уравнение в виде
m
. Область
)0(D
является областью устойч
какой-либо внутренней точки этой област
1
и
Π
ий полином (5.39),
можем , подтвер-
2
Π
,
пользуясь
дить устойчивость системы для выбранных значений параметров
1
Π
и
2
Π
.
Если область
)0(D
отсутствует, то при любых значениях па-
раметров
1
Π
2
Π
система
D – разбиени по одному параметру
0
П
П
1
D
(2)
D
(4)
D
(4)
Δ∞
=0; 0< <
ω
ι
ω
=0
ω=ω
i
Δ
=0
Δ
<0
2
D
(2)
D
(2)
>0
D
(0)
Δ
Δ
<0
ω±∞
=
Рис. 5.36. Особая прям
пересекает D-
ая с
∞<ω<
i
0
причем
кривую в нескольких точках,
в одной определитель
Δ
меняет знак
0
П
1
П
2
D
(2)
D
(2)
D
(3)
D
(3)
D
(4)
D
(0)
ω
=0
/ /
/ /
/
/
/
/
Δ
>0
ω=±∞
/
/ /
/ /
/ /
/
/
/
/ /
/ /
/
/
/
/ /
/ /
/ /
/
/ /
////////
//
/////
/
//
/
//
/
//
/
ми, соответствующими частотам
ωω∞
//
Рис. 5.38. D-кривая с двумя особыми
прямы
и
ii
=0 =
0
П
1
П
2
Δ∞
=0; 0 <
ω
i
<
ω=±∞
Δ
>0
ω
=0
=0
Δ
>0
Δ
Рис. 5.37. Особая прямая с
есекает D-кривую в нескольких
точках, причем в них определитель
принимает нулевое значение,
не меняя знака
0< <
ω∞
Δ
i
пер
49
