Афанасьев А.А. Математические основы теории систем управления
Подождите немного. Документ загружается.

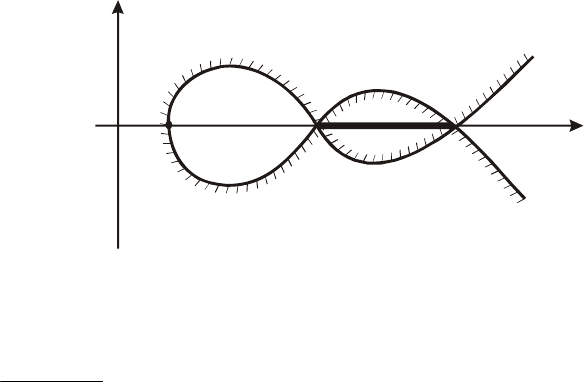
)λ()λ()λ(
110
0
=
Π
+
= DDD
Такая запись предполагает, что параметр
1
. (5.47)
Π
, влияние которого на
ь исследуется, вхустойчивост одит в характеристическое уравнение
линейно.
Найдем значение пара-
метра
1
Π
, выводящее систе-
му на границу устойчивости.
это коВ м случае рнями поли-
нома будут комплексно-
сопряженные мнимые числа
ω
λ
j
±
=
. (5.48)
После подстановки (5.48) в
(5.47) получим:
)ω()ω(
)ω(
ω(
1
0
1
jD
jD
−=Π
, (5.49)
т.е. параметр
1
Π
определится как комплексное число. С точки зре-
ния физической реализации этого параметра нас будут интересо-
вать значения его вещественной части, при которых система будет
устойчивой.
)
0
D
(2)
D
(1)
D
(2)
D
(0)
X
jY
ω
=+
∞
ω
=
–
∞
ω
=0
Рис. 5.39. D-кривая в плоскости одного
параметра, имеющего вещественную (X)
имнимую (Y) части
jYX +=
-
граф ве
сла мог
Задаваясь значениями
ω
от -∞ до +∞, можем получить годо
ктора (5.49).
В силу четности первого гае о
)(
ω
X
и нечетности вто-
рого слагаемого
)ω(
Y
, годогра относительно
оси (рис.5.39).
ф будет
D – кривую можно построить, задав
∞, т ассчи
и
симметричен
вещественной
аясь значениями
ω
от 0 до
+ .е. по формуле (5.49) р тать только половину
D
– кривой,
а затем дополнить зеркальным отображением относительно веще-
ственной ос
X
.
Пробегая мнимую ось комплексной плоскости корней снизу
верх (рис.5.35.а), будем пробегать ее об
один раз. Поэтому штриховка у этой кривой одинарная.
р
й к
в вещественной
в раз –
D
– кривую только
D
– кривая является г аницей
D
– разбиений с различным
числом правых корней. Область, у которо все орни левые
)0( =m
, я ляется областью устойчивости. Интервал
50
о нутри этой области задает интервал значений параметрси в а
Π
,
при которых система устойчива. На рис.5.39 этот интервал показан
жирным отрезком оси
X
.
D– разбиение при нелинейном вхождении параметров
в коэффициенты характеристического уравнения
1
Π
и
2
Π
Допустим два параметра входят в характеристиче
ское уравнение нелинейно
-
D
(5.50)
0),λ,(
21
=
Π
Π
. (5.50)
ω
λ
j
=
Подставляя в и выделяя вещественную и
плексн выражения, получим соответственно
мни-
двамую части ком
уравнения:
ого
.0),ω,(
212
=ΠΠ
;0),ω,(
211
=
Π
Π
f
(5.51)
даваясь значениями
ω
, можем решить их тем или ины
параметров
f
За м
тодом относительно неизвестных
ме-
1
Π
и , т.е. для
2
Π
за-
данного
ω
получим точку на плоскости параметров
1
Π
и
2
Π
.
Следовательно, уравнения (5.51) позволяют получить
D
–
кривую - образ мнимой оси на комплексной плоскости корней ха-
рактеристического уравнения.
При перемещении вдоль
D
– кривой в направлении роста час-
тоты
ω
штриховка наносится слева, если определитель матрицы
Якоби неявных функций
2
2
1
2
2
1
1
1
Δ
Π∂
∂
Π∂
∂
Π∂
∂
Π∂
∂
=
ff
ff
(5.51)
положителен.
51
5.
е) базируются на использовании характеристиче-
ю вычислительную задачу, особенно в
чных особенно-
тей
ации по полученному характеристическому полиному
х уравнений,
представленных в нормальной форме Коши [11, 20, 48].
5.5.
венные
исла матрицы.
Обычно конфигурация этой области либо наперед задана
г, полоса, ко
геометричес
Методы локализации дают информацию об интегральном
л матрицы, не указывая о
ется достаточной в первом приближении
ля суждения об устойчивости системы. Ее це
5. МЕТОДЫ ОЦЕНКИ УСТОЙЧИВОСТИ, НЕ СВЯЗАННЫЕ
С ПОСТРОЕНИЕМ ХАРАКТЕРИСТИЧЕСКОГО
ПОЛИНОМА
Классические методы исследования устойчивости (алгебраи-
ческие, частотны
ского полинома. Методу тем развертывание векового определителя
с целью получения указанного полинома представляет достаточно
трудоемкую самостоятельну
системах большой размерности.
Все методы построения характеристического полинома, в том
числе свободные от действия частных промежуто
с матриц, например типа вырождения ( к таким методам отно-
сится метод Леверрье и его модификации), аккумулируют ошибки
при округлениях. В результате физически устойчивая система при
ее идентифик
может трактоваться как неустойчивая.
Оценка неустойчивости системы может производиться на ос-
нове анализа матрицы исходных дифференциальны
1. ПРИБЛИЖЕННАЯ ОЦЕНКА УСТОЙЧИВОСТИ НА ОСНОВЕ
МЕТОДОВ ЛОКАЛИЗАЦИИ СОБСТВЕННЫХ ЧИСЕЛ МАТРИЦЫ
Методы локализации собственных чисел матрицы позволяют
указать ту часть (область) комплексной плоскости корней характе-
ристического уравнения, в которой расположены все собст
ч
(кру льцо и т.д.), либо представляет пересечение задан-
ных ких фигур.
расположении всех собственных чисе
месте расположения каждого конкретного числа.
Эта информация явля
д нность заключается в
52

том, что она может быть получена простыми легко реализуемыми
ствами.
Ориентировочное знание области распределения всего спек-
позволяет указать первона-
параметров системы.
Круги (неравенства) Гершгорина
В 1931 г. С. А. Гершгорин пред
мето
сред
тра собственных значений матрицы
чальные значения важнейших
ложил простой метод локали-
зации собственных чисел матрицы. Согласно этому ду все соб-
ственные числа
i
λ
квадратной матрицы
[
]
A
размерности n распо-
ложены в пересечении областей
D
и
'D
. Область
D
явл етя ся объе-
динением n круговых областей, задаваемых неравенствами:
),,2,1( niPa
iiii
K
=
≤
λ
−
, (5.52)
∑
=
=
n
l
ili
aP
1
-сумма всех элементов i-ой стгде
≠
ij
атрицы без диагонального элемента.
Область
D
′
является объединением n круговых областей, за-
ваемых неравенствами:
роки по модулю
м
да
),,2,1( niQa
iiii
K
=
≤
λ
−
, (5.53)
где
∑
=
n
ii
Q
- сумма
≠
=
ki
k
k
a
1
всех элементов i-го столбца по модулю
без диагонального элемента
.
Уравнение состояния
[]
xA
dt
xd
=
(5.54)
является устойчивым, если пересечение областей будет на-
ходиться слева от мнимой оси комплексной плоскости .
DD
′
λ
Локализация собственных чисел матрицы
[
]
A
по Гершгорину
включает следующие действия:
53
1. Вычислить строчные и столбцовые суммы матрицы
уравнения (5.54), учитывая диагональные элементы
о при суммировании опускаются).
2.
На плоскости комплексного переменного
i
P
не
i
Q
[]
A
ii
a
( ни
λ
a
D
построить сис-
тему из 2 кругов с центрами в точках и радиусами,
равными (для кругов объединения и (для
кругов объединения
n
i
P
ii
)
n
i
Q
n
D
′
).
Пересечение этих объединенных областей и укажет эту
часть комплексной плоскости, в которой все собст-
вен
,
D
расположены
D
′
ные числа
i
λ
матрицы
[]
A
.
ПРИМЕР 5.3
Имеем систему дифференциальных уравнений (5.54) 4-го порядка с матри-
цей
[]
A
вида
⎡
−− 00,25,5
[]
⎥
⎥
⎥
⎥
⎦
⎢
⎢
⎢
⎢
⎣
−−
−
−−
=
1,24,13,01,0
00,44,35,0
1,021,33,0
A
.
Области
D
и
D
′
определяют-
ся следующими неравенствами:
Область
D
⎤
−
1,
1,32
;8,11,2
,9,30,4
,5,21,3
,3,55,5
4
3
2
≤λ−−
≤λ−−
≤λ−−
≤λ−−
О
1
бласть
D
′
-5,5
-3,1
-5-11
0
3
∅
⋅
2
5
,
3
∅
⋅
2
5
,
7
+1
1
+
j
D
D’
-3 -1-7-9
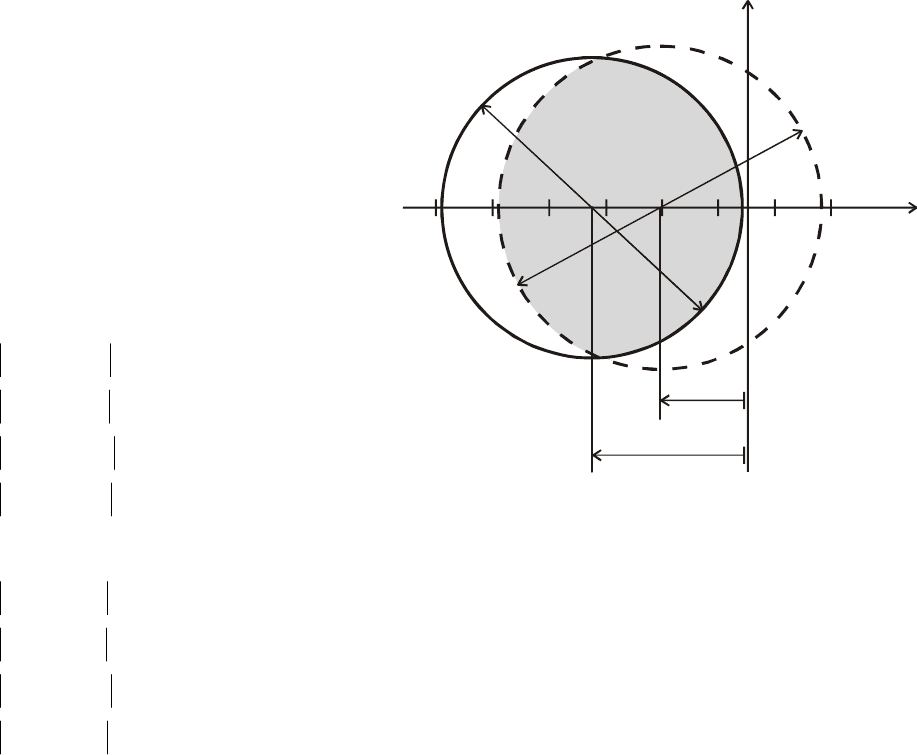
Рис.5.40. Пересечение объединений кругов D и D`-
область локализации собственных чисел
матрицы А из примера 5.3
[]
.2,3
4
≤λ−
На рис. 5.40 указано пересечение областей
D
,
D
1,2
1,3
5,5
1
−
≤λ−−
≤λ−−
,7,30,4
3
2
≤λ−−
,7,5
,9,0
′
. Видим, что все собствен-
ные матрицы левые, т.е. система (5.54) устойчива
[]
A
.
54
Метод Гершгорина локализации собственных чисел матрицы
ется наиболее прост
тую) оценку границ
Существуют другие более точные методы локализации [48],
связан
, вместо
кругов, овалов Кассини. Поэтому метод Гершгорина наиболее при-
емлем для ее устой-
Расщепление матриц
Локализация собственных чисел матрицы может произво-
ся на основе те
им
явля ым. Он дает сравнительно грубую (более
прос спектра матрицы.
использование которых о с применением более трудоемких
операций. Например, метод Брауэра требует построения
оперативной оценки матрицы с точки зрения
чивости.
дить ории проекторов.
Как известно (см. главу 2), представление матрицы с простым
спектром через проекторы и собственные числа еет такой вид:
[]
[
]
[
]
[
]
PPPA
n
n
λ
+
+
λ
+
λ= K
,
2
2
1
1
г
[]
,2,1(, jP
j
j
K
), nλ
.
=
де -
Допустим, первые
собственные числа и проекторы матрицы
[]
A
)( mn
−
собственны
спектра матрицы на две части
Введем в рассмотрение следующие суммы:
]
, (5.55)
де - левый и правый прое
х чисел расположены в
левой, остальные - в правой полуплоскости.
Расщепление
m
P(A
[] [][] [
∑∑
−
==
n
k
mn
k
PPP
21
)(;) A
+−==
mnkk 11
[][]
г кторы матрицы
21
)(,)( AA PP
[
]
A
, со-
ответствующие
[
]
A
, лежащим слева собственным числам матрицы
и справа от мнимой оси. Считаем, что спектр матрицы не лежит на
мнимой оси.
Ранги матриц и
[]
1
)( AP
[
]
2
)( AP
соо
праведливо равенство
тветственно равны числам
)( mn −
и
m
. Для введенных проекторов с
[]
[
]
EPP
=
+
21
)()( AA
. (5.56)
55

, соответствующую
р
Рассмотрим последовательность матриц
екуррентной формуле
[] [] []
(
)
1
1
2
1
−
+
+=
nnn
AAA
, (5.57)
где
K,2,1=n
;
[] []
AA =
1
.
∞
→n
справедливо Можно показать [11], что для
[]
(
)
[]
(
)
[
]
AA PPA
12
−
=
. (5.58)
матрицы
∞
Будем называть расщепителем
[
]
A
матрицу
()
[]
[]
−= AR
1
A
∞
. (5.59)
2
Из формулы (5.56), (5.58), (5.59) следует:
()
[]
()
[]
AA REP +=
2
1
1
, (5.60)
()
[]
()
[]
AA REP −=
2
2
. 61)
Формулы (5.59) - (5.61) позвол етить на вопрос, как ло-
1
(5.
яют отв
кализованы собственные числа матрицы
[
]
A
:
1.
Если расщепитель матр
()
[]
ER
2
1
=A
ицы , то весь спектр матри-
цы лежит в левой полуплоскости. В этом случае
[
]
EA −=
.
∞
2 ли расщепитель матрицы
[]
()
E
2
1
−
, то весь спектр матри-
ости. В этом случае
. Ес
R =A
цы лежит в правой полуплоск
[
]
EA =
∞
.
сщепляться и в более Спектр матрицы на две части может ра
сложном случае. В качестве исходной матрицы возьмем смещен
ную матрицу
-
[]
[
]
EAA
=
1
σ
−
, (5.62)
где - вещественное число.
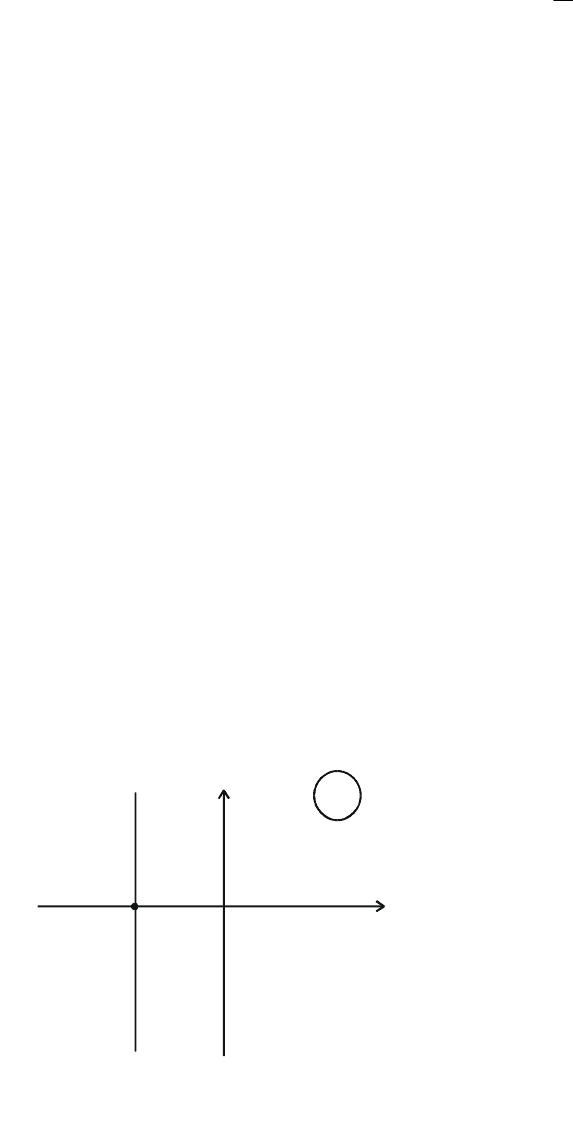
Прямая
σ
σ
=λRe
левее и
(рис. 5.41) раз
две части: правее прям
деляет спектр матрицы
[]
A
на
ой
σ
=
λ
Re
. Предполагаем, что на
. самой прямой нет точек спектра
56
Части с р пектра, асположенной левее прямой
σ
=λRe
, будет
соответствовать проектор
(
[
)
]
1
1
AP
.
[
]
1
A
Собственным числам матрицы , находящимся правее пря
ой
σ=λRe
, будет соответствовать проектор
()
-
м
[
]
2
1
AP
.
Расщепитель смещенной
(
)
[
]
1
AR
ищется по рекуррентной
формуле (5.57). Если получим
()
[]
ER
1
=A
, о (5.60),
2
то, согласн
1
(
)
[]
EP
=
1
1
A
,
(
)
[
]
2
1
=
AP 0
[
]
A
и, следовательно, спектр матрицы будет р
ой
асполагаться левее
прям .
величину
σ=λRe
σ
, можем оценить запасВарьируя устойчивости
матрицы
[]
A
, т.е. найти такое значение
0
σ
=
σ
<
0
, которое макси-
мально близко к вещественной части крайнего собственного числа.
Определение проектора матрицы
[
]
A
, соответствующего час-
ти спектр ого внутри заданной области
ть льная полоса
а, расположенн
β<λ
<
α
Re
а) Заданная облас - вертика (рис. 5. 42)
трицы
[
]
{
}
EA
β
−
, соответствующий
енным
Проектор смещенной ма
β=Reλ
собственным числам, располож вее оси ле :
()
[]
(
)
[
]
EAEA
β
−
+
=
β
− REP 5,0
1
, (5.63)
де - расщепитель матрицы
()
[]
EA β−R
[
]
{
}
E
β
−
A
.
Аналогично, проектор матрицы
г
[
]
E
α
−
A
, соот
собственным значениям, лежащим
ветствующий
слева оси
α=
λ
Re
,
(
)
[
]
(
[
AE
)
]
EA
α
−
+
=
α
−
RE5,0
1
P
(5.64)
где
Рис. 5.41. Комплексная плоскость
с прямой
Re λσ=
λ
+j
,
[
(
)
]
EA
α
−
R
- расщепитель
[
]
{
}
E
α
−
A
.
Если из (5.63) вычесть (5.64),
то получим выражение для проек-
+1
0
σ
тора матрицы
[
]
, соответствую-
щего собственным числам, з
ченным внутри полосы
A
аклю-
57

β<λα e
:
()
[]
< R
(
)
[]
(
)
[
]
EAEA
α
−
−
β
−
=β<λ<α RRP Re
, (5.65)
δ<λ
<
γ
m
I
б) Заданная область - горизонтальная полоса
Аналогичные рассуждения позволяют записать ормулу для
проектора матрицы
[]
A
, соответствующего собственным числам,
заключенным внутри горизонтальной полосы (рис. 5.42)
<
ф
γ
m
I δ<λ
:
()
[]
()
[]
(
)
[
]
EAEA γ
−
−
−
δ
−
−
=δ
<
λ< jRjRI
m
γP
Если
собственные
. (5.66)
проекторы окажутся равными единичн
числа матрицы
ой матрице, то все
[
]
A
, будут находиться в вертикальной
ла
и оризонтальной полосе. При нулевом значении указанных про-
екторов собственные чис матрицы
ли г
[
]
A
находятся вне этих полос.
в) Заданная область –
прям
β<λ
оугольник (
<
α
,
Re
δ
<λ<
γ
m
I
)
Проект
ориентирова
венные числа
олучим ,
(5.65)
):
ор матрицы ,
нны
в
2-3-4, рис. 5. 42),
перемножая фор-
и (5.66) (см. разд.
}
)
+j
λ
α
[]
A
й на собст-
нутри пересе-
чения полос ( внутри прямо-
угольника 1-
п
мулы
2.12
()
[]
()
[]
()
[]
{
()
[]
(
[
{}
,*
*
Im;Re
EAEA
EAEA
γ−−−δ−−
α−−β−=
]
=
δ
<
<
γ
β<λ<
α
jRjR
RR
P
(5.67)
проектор (5.67) отличен от нуля, то хотя бы одно собст-
венное число матрицы заключено внутри прямоугольника 1-2-
Если
[]
A
+
4
3
β
0
2
1
γ
j
Рис. 5.42. Прямоугольник 1 - 4 - пересечение
бесконечных
и гори
j
δ
вертикальных
зонтальных полос
58
3 ю матрицу, то весь -4. Если этот проектор представляет единичну
спектр матрицы находится внутри прямоугольника 1-2-3-4.
Покрывая комплексную плоскость прямоугольной сеткой,
можем мат-
рицы.
[]
A
, очевидно, ответить на вопрос о локализации спектра
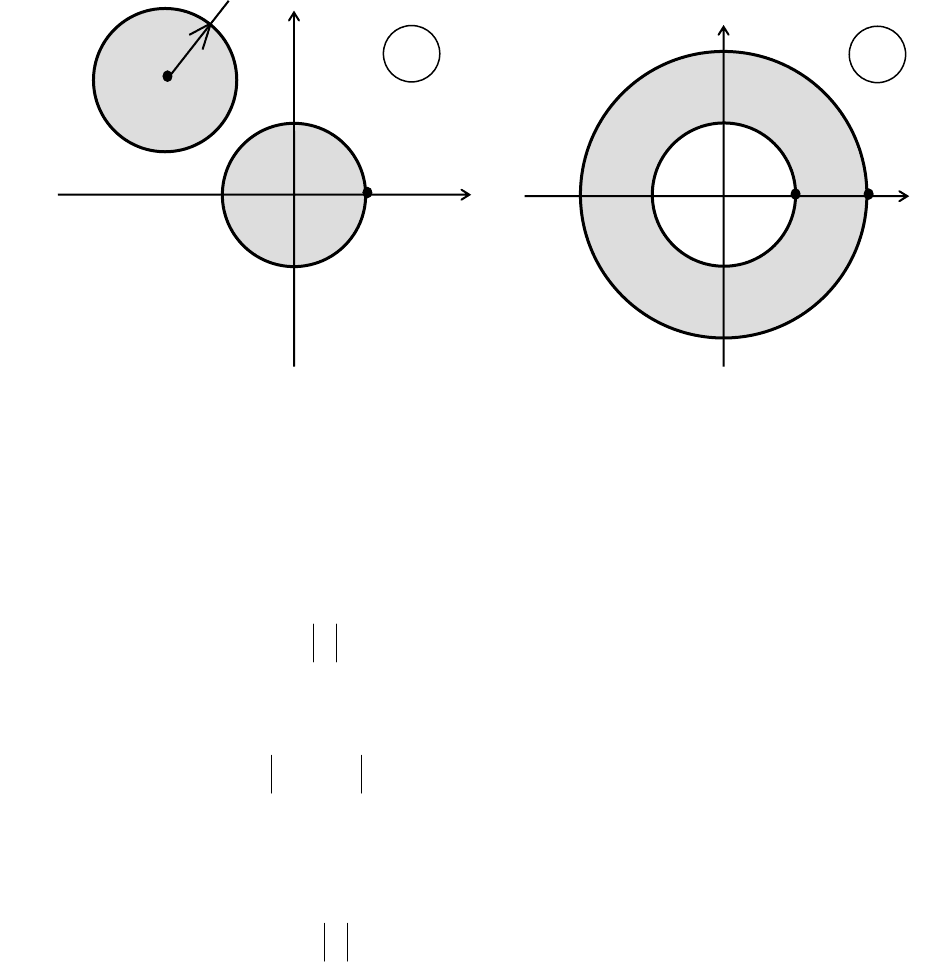
г) Заданные области –круг, кольцо
Известны формулы [11] для проекторов круга радиусом
ρ
(рис. 5.43а):
(
)
[
]
(
)
[
]
ρ
+
=
ρ
<
λ BREP 5,0
, (5.68)
где
[]
[
]
}
[
{
ρ
= AAB
{
ρ+ E
]
}
1−
ρ− E
;
[
]
(
)
[
]
ρ
+
=
ρ
<
λ
−λ
,00
5,0)( BREP
, (5.69)
где
[]
[]
()
{
}
[
]
(
)
{
}
1
00,0
−
ρ
λ+ρ−λ−ρ+= EAEB
кольца (рис.
5.43,б):
A
(
)
[
]
(
)
[
]
(
)
[
]
β α
−
=
β
<
λ
<α BB RRP
. (5.70)
ρ
0
0
+
+
j
β
α
+
0
+
j
λ
0
ρ
а
)
б
)
λ
λ
Рис. 5.43. К вычислению проекторов матрицы [A], соответствующих круговым (а) и
кольцевым (б) областям
59
