Афанасьев А.А. Математические основы теории систем управления
Подождите немного. Документ загружается.

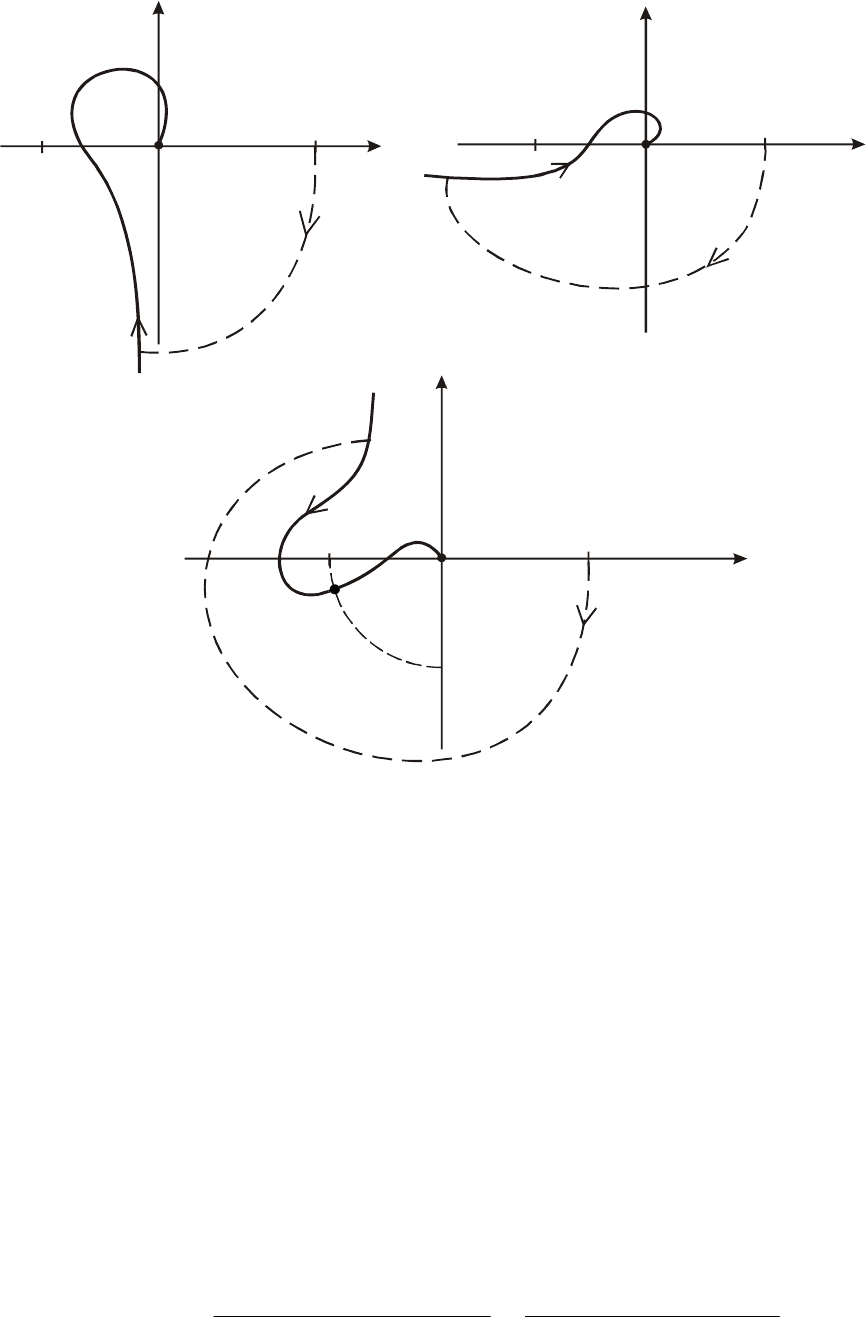
-1
0
+1
+j
б)
-1
0
+1
а)
+j
-1
0
+1
в)
+j
+
-
ω
=0
ω=∞
(
β
≠
0)
k
/
β
3
ν=1
ω=∞
ν=3
ω=0
(β≠0)
ω=0
(β≠0)
k
/
β
k
/
β
2
ω=0
(β=0)
ν
=2
ω=0
(β=0)
ω=∞
ω=0
(β=0)
ω
c
Рис. 5.22. Замкнутая система устойчива: расположение годографа
)( ωjW
для
систем, находящихся после размыкания на границе апериодической устойчивости
(а, б, в – астатические системы соответственно 1-го, 2-го и 3-го порядков)
2.2. Граница устойчивости колебательная
Аналогичным образом может применяться этот критерий и
при наличии у характеристического полинома разомкнутой систе-
мы пары сопряженных мнимых корней (
s
01γγ,
ωj
±
=
+
1γγ,
βs
). Сдвигают
эти корни в левую полуплоскость, считая
0
ωj
±
−
=
+
, а затем
рассматривают частотный годограф разомкнутой системы
)ω(
j
W
при .
0β →
Пусть передаточная функция разомкнутой системы имеет вид
)(]ω)β[(
)(
)())((
)(
)(
2
0
2
1γγ
sQs
skN
sQssss
skN
sW
++
=
−−
=
+
.
30
Из выражения для частотной характеристики
)ω(]ω)βω[(
)ω(
)ω(
2
0
2
jQj
jkN
jW
++
=
следует:
1)
2
0
0β
ω
)0(
k
W =
→
;
2)
приращение аргумента комплекса
2
0
2
ω
при из-
менении
ω
от
ε
до
εω
)βω( ++= jA
0
+=ωω
0
-
0
−= ω
0
+
(
ε
– бесконечно
малое положительное число) с условиями
0
ωε ; εβ
<
<
равно (
π-
)
<<
2
.
Следовательно,
π)ω(argΔ
0
-
0
ωωω
=
+
<<
jW
.
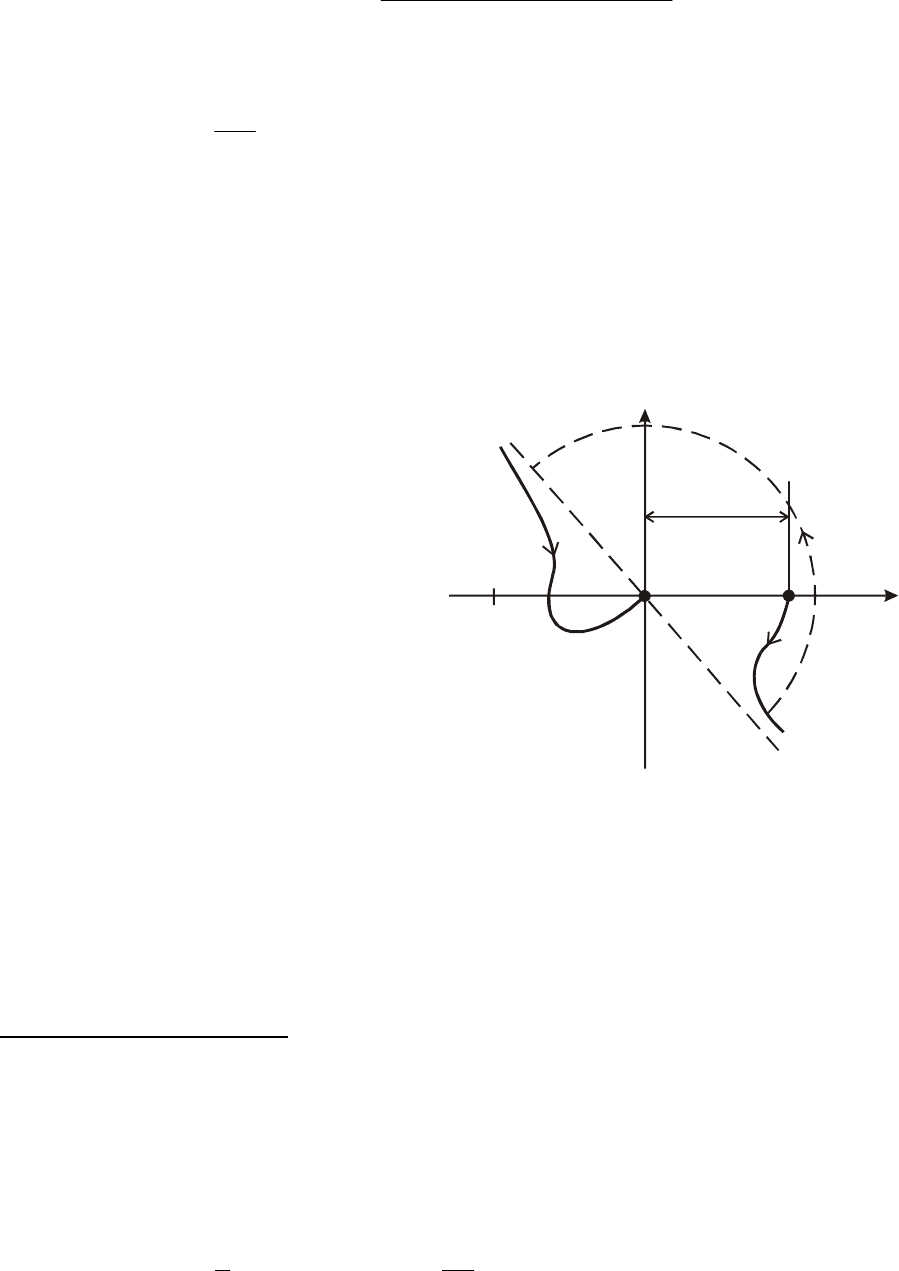
Участок годографа час-
тотной характеристики
)ω(
j
W
для интервала частот
рис.5.23 показан
пунктирной линией в виде по-
луокружности достаточно
большого радиуса, диаметром
которой является отрезок
асимптотической прямой го-
дографа, проходящей через
начало координат. При
линия годографа асимптотически приближается к
этой прямой, уходя в диаметрально противоположных направлени-
+
<<
0
-
0
ωωω
(
0
=βω→ω )0
+j
+1
0
-1
2
Действительно, комплексу в окрестности
можно придать вид: , где
верхние знаки соответствуют , нижние - ; и - беско-
нечно малые второго порядка.
2
0
2
)( ω+β+ω= jA
εββω+β+ε
0
2
(2j m
ω=ω
+
00
εω=ω=ω m
m
00
βω+εω±≈ω±=
000
22)2 jA
ε−ω
0
ε+
2
β
εβ
=ω
−
0
Очевидно
0tgarcarg =
ε
β
=
−
A , π−=
ε
−
β
=
+
tgarcarg A , π−=−=
−+
ω∠ω∠ω
Δ
+−
AA
A
argarg
arg
00
.
ω+ε=ω
00
+
K/
ω
0
2
ω=∞ ω=
0
ω=
0
−
ω
−ε
0
Рис. 5.23. Замкнутая система устойчива:
расположение годографа Wj для
системы, находящейся после размыкания на
границе колебательной устойчивости
()
ω
31
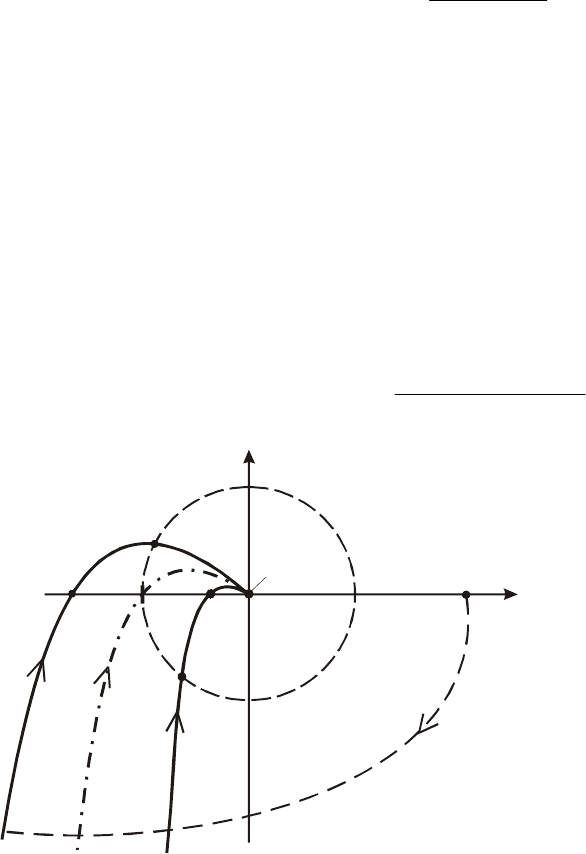
ях в бесконечность. Положение асимптотической прямой задается
аргументом комплекса
)(
)(
0
0
ω
ω
=
jQ
jkN
B
.
Видим, что в рассматриваемом случае годограф частотной ха-
рактеристики не охватывает точку (-1), следовательно, замкнутая
система устойчива.
ПРИМЕР 5.2
Обратимся к предыдущему примеру 5.1, в котором рассматривалась
астатическая система первого порядка (
1γ
=
) с передаточной функцией в разомк-
нутом состоянии
)1)(1(
)(
21
++
=
sTsTs
k
sW
. (5.26.)
Частотные годографы этой
системы для трех значений коэф-
фициента усиления представле-
ны на рис.5.24. Кривая 1 построе-
на п
гр
k
k
ри
k
<
и соответствует ус-
тойчивому состоянию замкнутой
системы. Кривая 3 – п
гр
k
и
соответствует неустойчивой замк-
нутой систем
ри
е.
1)ω(
π
−
k >
Критерий Найквиста позво-
ляет определить граничное значе-
ние коэффициента усиления ,
при котором частотный годограф
(кривая 2) проходит через точку
(-1):
гр
k
W
=
,
здесь – частота, при кото-
рой годограф пересекает отрицательную действительную полуось.
π
ω
При частоте имеем
π
ωω =
0)ω(Im
π
=
jW
. (5.27)
Так как числитель передаточной функции (5.26) вещественный, то условие
(5.27) выполняется при обращении в нуль мнимой части знаменателя
W
:
)ω( j
32

[]
0)ω1(ω)ω1)(ω1(ωIm
21
2
ππ2π1ππ
=−=++ TTTjTjj
.
Отсюда:
или
01ω
21
2
π
=+− TT
21
π
1
ω
TT
=
. (5.28)
На этой частоте знаменатель представляет действительную величину, равную
[]
).(ω)ω1)(ω1(ωRe
21
2
π2π1ππ
TTTjTjj +−=++
Обратим внимание, что в соответствии с формулой (5.28) величина не
зависит от коэффициента усиления . Следовательно, имеем с учетом (5.28)
π
ω
k
21
21
2
π
11
)(
)(Re)ω(
TT
k
TT
k
jWjW
+
−=
+ω−
=ω=
π
π
. (5.29)
После приравнивания этой формулы к отрицательной единице
21
11
TT
kk
гр
+==
. (5.30)
Выражение (5.30) было получено ранее в примере 5.1 исходя из критерия
Гурвица. Формуле (5.29) теперь можно придать вид
гр
kkjW
−
=
)ω(
π
.
3.Система в разомкнутом состоянии неустойчива
Пусть характеристический полином разомкнутой системы
имеет l корней в правой полуплоскости. В соответствии с
формулой (5.17) имеем для приращения аргумента
)(sL
)ω(
j
L
при из-
менении от 0 до +
∞
ω
)2(
2
π
)ω(argΔ lnjL −=
. (5.31)
Потребуем, чтобы система была устойчива в замкнутом со-
стоянии. Для частотного годографа ее характеристического поли-
нома
)ω(
j
D
, согласно критерию Михайлова, должно выполняться
равенство:
njD
2
π
)ω(arg Δ
ω0
=
∞<<
. (5.32)
33

Введенная выше вспомогательная функция
)ω(
)ω(
)ω(1)ω(
jL
jD
jWjF =+=
должна иметь, согласно (5.31), (5.32), следующее приращение ар-
гумента при изменении
ω
от 0 до +∞:
2
π2π)2(
2
π
2
π
)ω(arg)ω(arg)ω(argΔ
l
llnnjLjDjF ==−−=Δ−Δ=
.
Отсюда следует формулировка критерия Найквиста:
Для устойчивости замкнутой системы автоматического ре-
гулирования необходимо и достаточно, чтобы частотный годо-
граф передаточной функции разомкнутой системы
)ω(
j
W
при из-
менении от 0 до +
∞
охватывал
ω
2l
раза в положительном на-
правлении точку (-1), где l – число правых корней характеристиче-
ского полинома разомкнутой системы.
Например, если передаточная функция разомкнутой системы
принимает вид
1
)1(
)(s
0
0
−+
++
=
K
K
n
m
sc
sbk
W
,
т.е. характеристический полином имеет отрицательный свободный
член , то число правых действительных корней l будет
равно нечетному числу ( и т.д.)
)1( −=
n
c
3,1=l
3
.
3
Свободный член характеристического полинома )())(()(
210 n
ssssssasL −−
−
=
K
равен
nrr
n
n
sssssaa KK
1210
)1(
+
−= ,
где
r
– число действительных корней.
Произведение двух комплексно-сопряженных корней по-
ложительно при любых значений и . Поэтому
22
ωα)ω-α)(ωα( +=+ jj
0)s(s
n1
α ω
r
>
+
K . Имеем также
. Поскольку
rnrn −
−−=− )1()1()1(
r
n − – число четное, то . Следовательно,
и, значит, правые комплексно-сопряженные корни не могут
обусловить отрицательный знак свободного члена .
1)1( =−
−rn
n
r
n
sssaa K
210
)1(−=
n
a
34
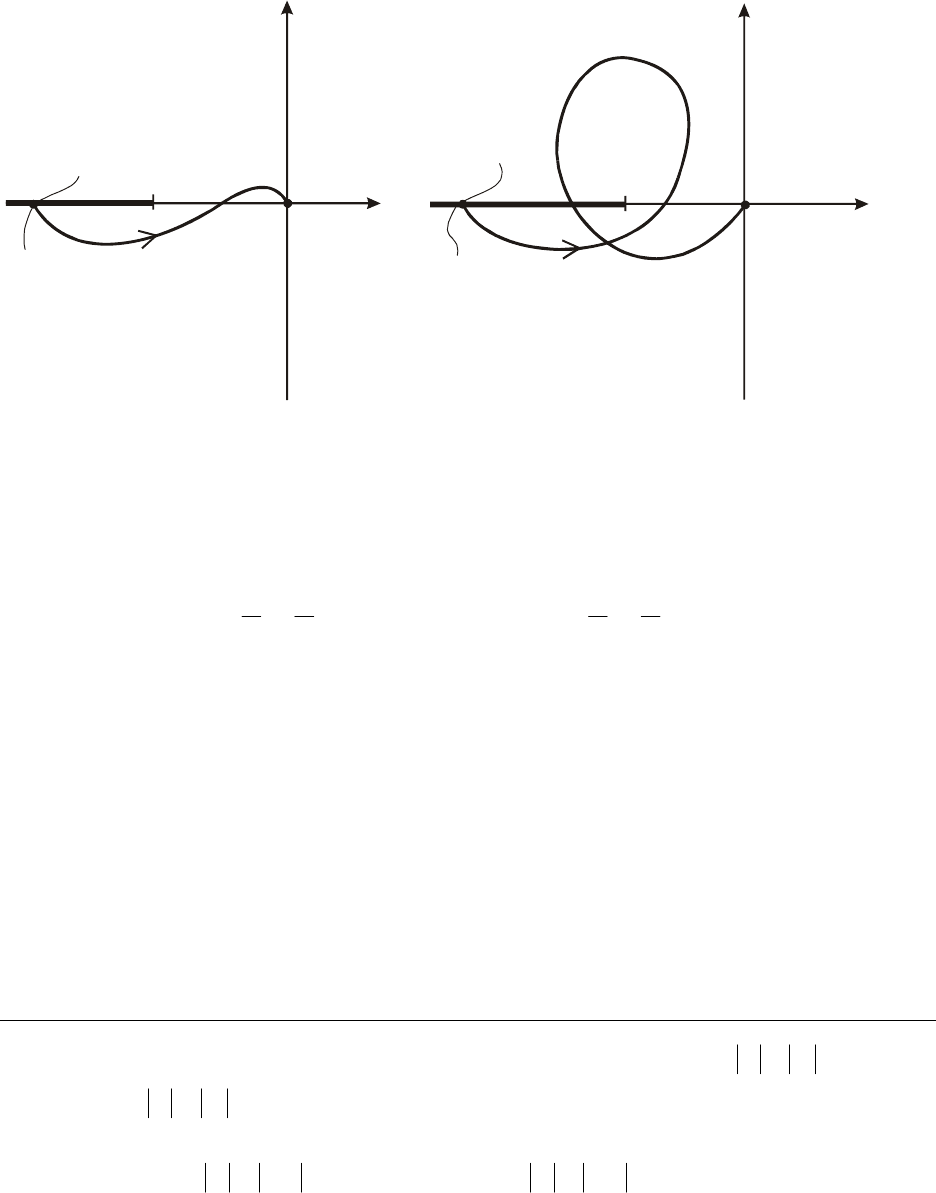
Годографы частотных характеристик разомкнутых систем, у
которых характеристические полиномы имеют один правый дейст-
вительный корень (
l
на рис.5.25,а), и три правых действитель-
ных корня (
1=
3
=
l
на рис.5.25,б), показаны на рис.5.25.
+1
+j
+1
0
-1
-k
+j
0
-1
-k
б)
а)
+
+
ω=0
ω=∞
l=
1
l=
3
ω=∞
ω=0
Рис. 5.25. Замкнутая система устойчива: годограф Wj для системы, имеющей
в разомкнутом состоянии характеристический полином с одним (а) и тремя (б)
правыми действительными корнями
()
ω
Точка (-1) охватывается годографом в положительном направлении
в первом случае
2
1
2
=
l
раза, во втором –
2
3
2
=
l
раза. Следователь-
но, в соответствии с критерием Найквиста обе системы в замкну-
том состоянии будут устойчивы.
Возможна другая формулировка критерия устойчивости Найк-
виста, не требующая подсчета числа охватов годографом точки (-
1). Эта формулировка базируется на определении числа переходов
частотного годографа
)ω(
j
W
через отрицательную полуось левее
точки (-1). Каждому переходу сообщают знак (плюс или минус) в
зависимости от направления перехода.
Если все
r
действительных корней левые, то
r
r
r
sssss KK
121
)1(−= , поэтому
[
]
0)()1(
110
2
>−=
+ nrr
r
n
ssssaa KK
n
a, т.е. всегда положительно.
r
действительных корней имеем правых, то Если из l
)()1()()1()1(
110110 nlrlr
l
nlrlr
lrr
n
ssssassssaa KKKK
+−−+−−
−
−=−−=
l
0
. Следователь-
но, при нечетных имеем
<
n
l
0>
n
aa , при четных – .
35
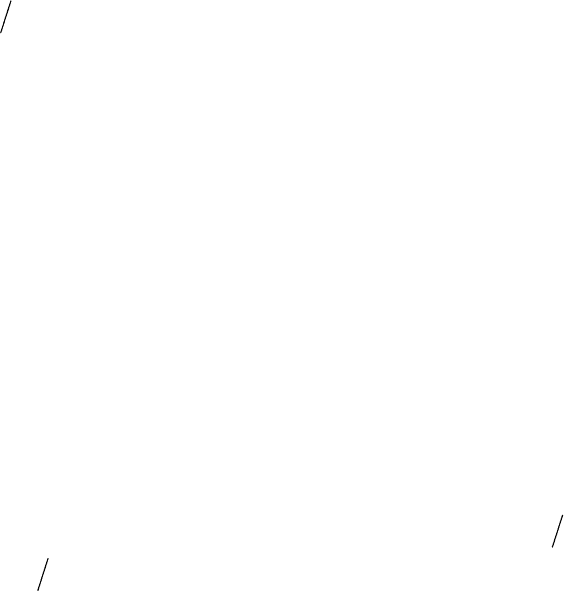
Переход считается положительным, если при возрастании
годограф переходит из верхней полуплоскости в нижнюю (т.е. в
положительном направлении – против часовой стрелки). Переход
будет отрицательным, если годограф пересекает отрицательную
ось снизу вверх (из нижней полуплоскости в верхнюю).
ω
Начало годографа (при
0ω
=
) на отрицательной полуоси ле-
вее точки (-1) принимается за половину перехода (рис.5.25).
Формулировка критерия Найквиста, базирующаяся на числе
переходов через полуось
(-1))(-
÷
∞
и пригодная для всех трех рас-
сматриваемых случаев, имеет такое содержание:
Для устойчивости замкнутой системы автоматического ре-
гулирования необходимо и достаточно, чтобы алгебраическая
сумма переходов частотного годографа передаточной функции
разомкнутой системы
)ω(
j
W
через отрицательную полуось левее
точки (-1) была равна
2l
, где l – число правых корней характери-
стического полинома разомкнутой системы.
Для систем, находящихся в разомкнутом состоянии на грани-
це устойчивости, число l считается равным нулю, а годограф
)ω(
j
W
берется с дополнением в бесконечности.
Например, на рис.5.22,в число переходов годографа для аста-
тической системы третьего порядка равно нулю (с учетом пунк-
тирного дополнения). На рис 5.21,б имеем годограф системы с
. Число переходов также равно нулю.
0=l
Наконец, на рис 5.25 показан годограф с нецелым числом пе-
реходов, для которых идентификация числа "охватов" точки (-1)
несколько затруднительна. Применение критерия Найквиста в по-
следнем варианте для этих случаев особенно эффективно. Видим,
что система на рис.5.25.а имеет
1
=
l
, а число переходов
)21(+
.
Для рис.5.25,б имеем
)23(+
перехода при
3
=
l
. Следовательно,
обе системы в замкнутом состоянии устойчивы.
Применение критерия Найквиста при использовании лога-
рифмических частотных характеристик
Отметим три очевидных обстоятельства:
36

1) Годограф частотной характеристики
)ω(
j
W
устойчивой сис-
темы пересекает отрицательную полуось при некоторой частоте
правее точки (-1) (кривая 1 на рис.5.24). Это значит, что ам-
плитудная логарифмическая характеристика для этой частоты
меньше нуля (отрицательна):
π
ωω =
0)ω(log20)ω(
ππ
<
=
jWL
.
Частота , для которой
с
ω 0)ω(
c
=
L
π)
π
, называется частотой среза. Она
меньше частоты (
π
ω ω(
−
=
ϕ
, рис.5.24).
Если годограф
)ω(
j
W
больше не пересекает отрицательную
полуось левее точки (-1), то выполнение неравенства
πc
ωω
<
(5.33)
является необходимым и достаточным условием для обеспечения
устойчивости замкнутой системы.
На рис.5.26 показаны амплитудно-фазовые частотные харак-
теристики астатической системы первого порядка из примера 5.1.
Кривые 1,2,3 амплитудных характеристик отличаются друг от дру-
га только коэффициентом усиления
k
.Для первой кривой –
,
гр
kk <
1
πc1
ωω
<
, для второй −
гр
kk
=
,
πc2
ωω
=
,
для третьей – , .
гр
kL log20
2
=
π
ω
c3
ω >
гр
kk >
3
При варьировании коэффициента усиления
k
сдвигаются
только амплитудные характеристики, фазовая характеристика оста-
ется без изменения. Только первая характеристика удовлетворяет
условию (5.33).
2) Годограф частотной характеристики
)ω(
j
W
пересекает отри-
цательную полуось левее точки (-1) (кривая 3, рис.5.24.) Имеем для
точек пересечения оси:
0)ω(log20)ω(
ππ
>
=
jWL
,
π)ω(arg)ω(
ππ
−=
=
jW
ϕ
.
3) Точки логарифмической фазовой характеристики
π)ω(
π
−
=
ϕ
,
для которых и пересечения горизонтальной прямой с ор-
динатой ( ) совершаются снизу вверх (в сторону возрастания
0)ω(
π
>L
π−
ϕ
),
при росте являются положительными переходами, сверху вниз –
отрицательными переходами.
ω
37

L
3
L
2
ω
,
c
-1
ω
,
c
-1
-20 дБ/дек
L, дБ
0
-40 дБ/дек
-60дБ/дек
10
4
ϕ,
рад
ω
π
ω
π
L
1
10
1
1
2
3
1/T
1
10
2
ω
C1
ω
C2
ω
C3
10
3
1/T
2
10
4
10
3
10
2
10
1
−π/2
−π
−3/2π
10
-1
Рис. 5.26. Логарифмические амплитудные (а) и фазовые (б) частотные
х
арактеристики астатической системы первого порядка из примера 5.1. с кривыми
1,2,3, имеющими соответственно коэффициенты усиления kk, kk, kk
123
<=>
гр гр гр
При этих условиях критерий устойчивости формулируется так:
Система автоматического регулирования устойчива тогда и
только тогда, когда алгебраическая сумма переходов левее часто-
ты среза (
c
ω
c
ωω0
<
≤
) равна
2l
, где l – число правых корней ха-
рактеристического полинома разомкнутой системы.
На рис.5.27 показаны логарифмические амплитудно-фазовые
характеристики для астатической системы третьего порядка, у ко-
торой l=0. Видим, что алгебраическая сумма переходов на частот-
ном интервале равна нулю. Следовательно, эта система в
замкнутом состоянии будет устойчивой.
c
ωω0 <<
38
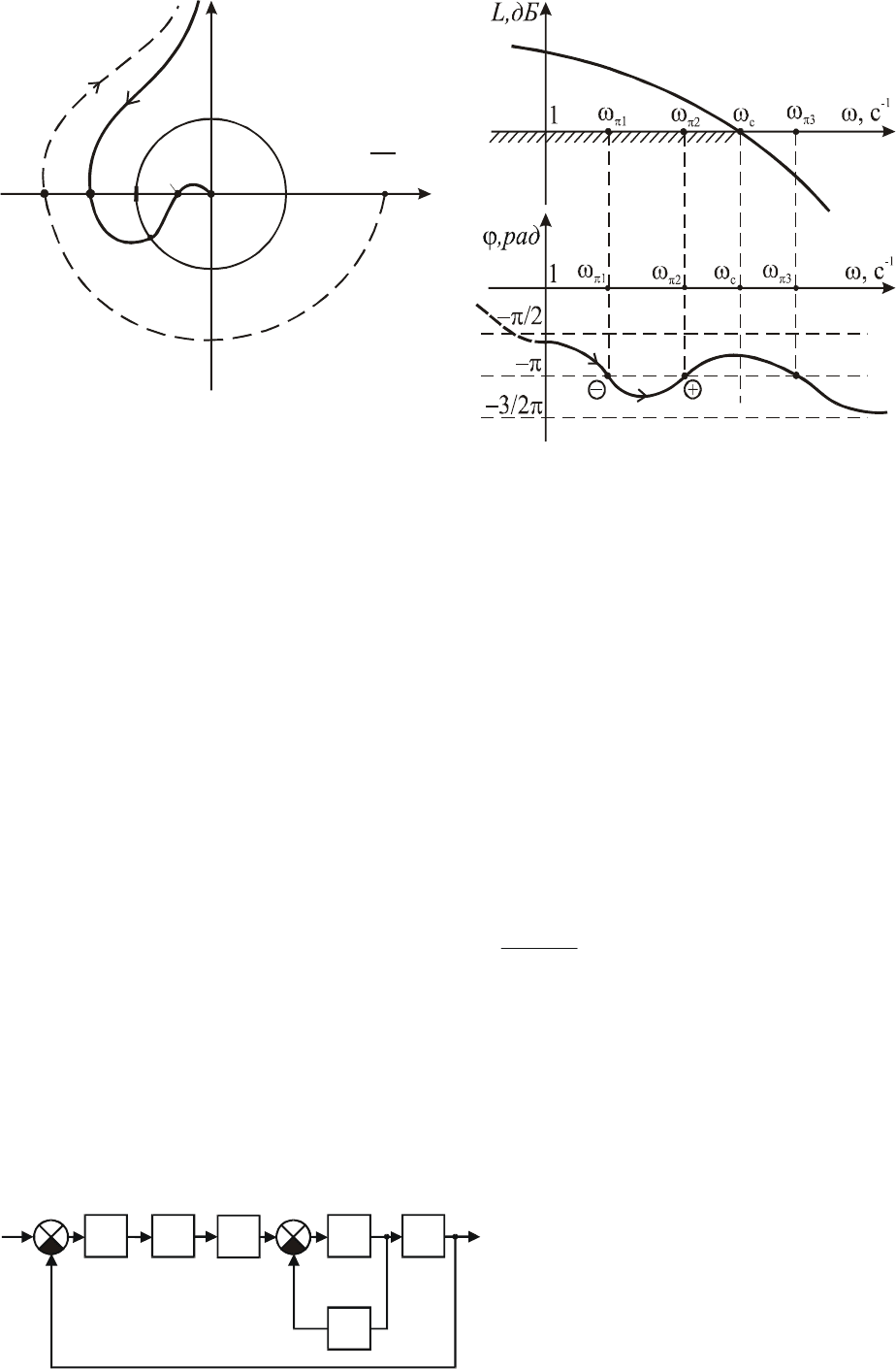
(+)
-1
ω
π
2
+1
+j
(-)
0
а)
ω
π
3
(β
≠0)
ω=0
ω=∞
ω
c
ω
π
1
k
β
3
б)
в)
Рис. 5.27. Годограф Wj (а), логарифмические амплитудная (б) и фазовая (в)
частотные характеристики астатической системы третьего порядка,
устойчивой в замкнутом состоянии
()
ω
Применение частотных критериев устойчивости
для систем с запаздыванием
Звено запаздывания имеет передаточную функцию вида
τs
τ
)(
−
= esW
(5.34)
Если это звено находится в прямой части системы и не охвачено
местной обратной связью (рис.5.28), то передаточная функция ра-
зомкнутой цепи имеет вид
τsτs
0τ
)(
)(
)()(
−−
== e
sL
skN
esWsW
, (5.35)
где – передаточная функция разомкнутой системы без запаз-
дывания.
)(
0
sW
Характеристическое уравнение замкнутой системы с запазды-
ванием
(
)()( += kNsLsD
будет трансцендентным. По-
этому для оценки его устой-
39
g
W
τ
x
Рис. 5.28. Структурная схема системы со
звеном запаздывания W в прямой части
τ
