Афанасьев А.А. Математические основы теории систем управления
Подождите немного. Документ загружается.

плоскости, то очевидно при изменении от –∞ до +∞ приращение
аргумента составит:
ω
)2(ππ)(π)ω(arg mnmmn
j
D
−
=
−
−
=Δ
. (5.17)
Таким образом, изменение аргумента характеристического
полинома однозначно связано с расположением его корней на ком-
плексной плоскости.
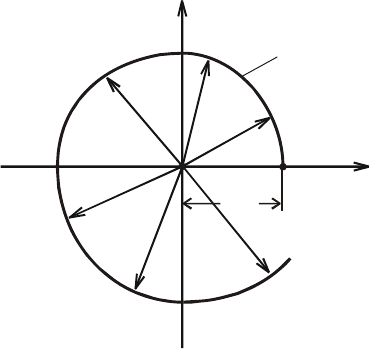
Построим годограф вектора
ω)(
j
D
, выделив его вещественную
и мнимую части
ω
1
ω
2
ω
3
ω
4
ω
5
ω
6
X
jY
0
a
n
Рис. 5.10. Годограф
х
арактеристического полинома
(годограф Михайлова)
Dj
()
ω
,
)(ωjω)(ω)
j
Y
X
(D
+
=
. (5.18)
Вектор
ω)(
j
D
, построенный в
декартовых координатах
ω),(
X
)(ω
jY
, при изменении от –∞ до
+∞ вращается и своим концом опи-
сывает кривую, которая называется
годографом характеристического
полинома
, или годографом (кривой)
Михайлова
(рис.5.10).
ω
Многочлен
(5.19)
L
K
++−=
=+++=
−−
−
4
2
2
42
2
ω
)ω)ω()ω(
nnn
nnn
aaa
jajaajX
−
4
4
ω
(
является четным относительно , т.е.
ω
)ω()ω(
−
=
X
X
. (5.20)
Многочлен
(5.21)
)ω-ω(
)ω()ω(jω)ω(
53
31
5
5
3
31
K
K
−+=
=+++=
−−
−−
nnn
nn
aaaj
jjaajY
ω
5
−
−
n
a
является нечетным относительно , т.е.
ω
)ω()ω( −−=
Y
Y
. (5.22)
Отметим, что при имеем:
0ω =
0(,)0( )0
=
= YaX
n
.
20
При
+∞=∞∞= )(ω
X
или
∞
-
,
+
∞
=
∞
)(
Y
или .
∞-
Знак предельных значений зависит от степени . При поло-
жительных значениях коэффициентов полинома имеем для
:
n
i
a
+∞=
ω
⎪
⎪
⎪
⎭
⎪
⎪
⎪
⎬
⎫
+∞=+∞==
−∞=+∞==
−∞=−∞==
+∞=−∞==
+∞===
;;;5
;;;4
;;;3
;;;2
;;;1
YXn
YXn
YXn
YXn
YaXn
n
и т.д.
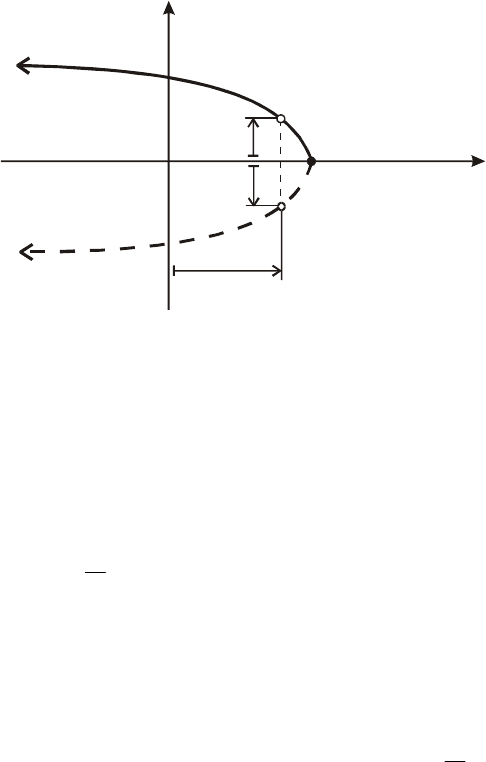
Уравнения (5.20) и
(5.22) свидетельствуют о
симметрии кривой Михайло-
ва относительно веществен-
ной оси (рис. 5.11).
Обычно ограничиваются
половиной интервала изме-
нения
ω, берут его от 0 до
+
∞, т.е. не фиксируют поло-
вину кривой, являющейся
зеркальным отражением дру-
гой половины относительно
вещественной оси. В этом случае при изменении от 0 до +
∞ и
при наличии корней только в левой полуплоскости приращение ар-
гумента
ω
ω)(
j
D
составит:
y
1
0
X
jY
ω=ω
1
-y
1
ω=−ω
1
ω=ω
0
x
1
ω→+∞
ω→−∞
Рис. 5.11. Симметрия годографа Михайлова
относительно вещественной оси
njD
2
π
)ω(arg
ω0
=Δ
∞+<<
. (5.24)
Отсюда следует формулировка критерия Михайлова.
Система будет устойчива тогда и только тогда, когда при
возрастании
ω от 0 до +
∞
вектор
ω)(
j
D
повернется на угол
n
2
π
,
где n — степень характеристического полинома.
21
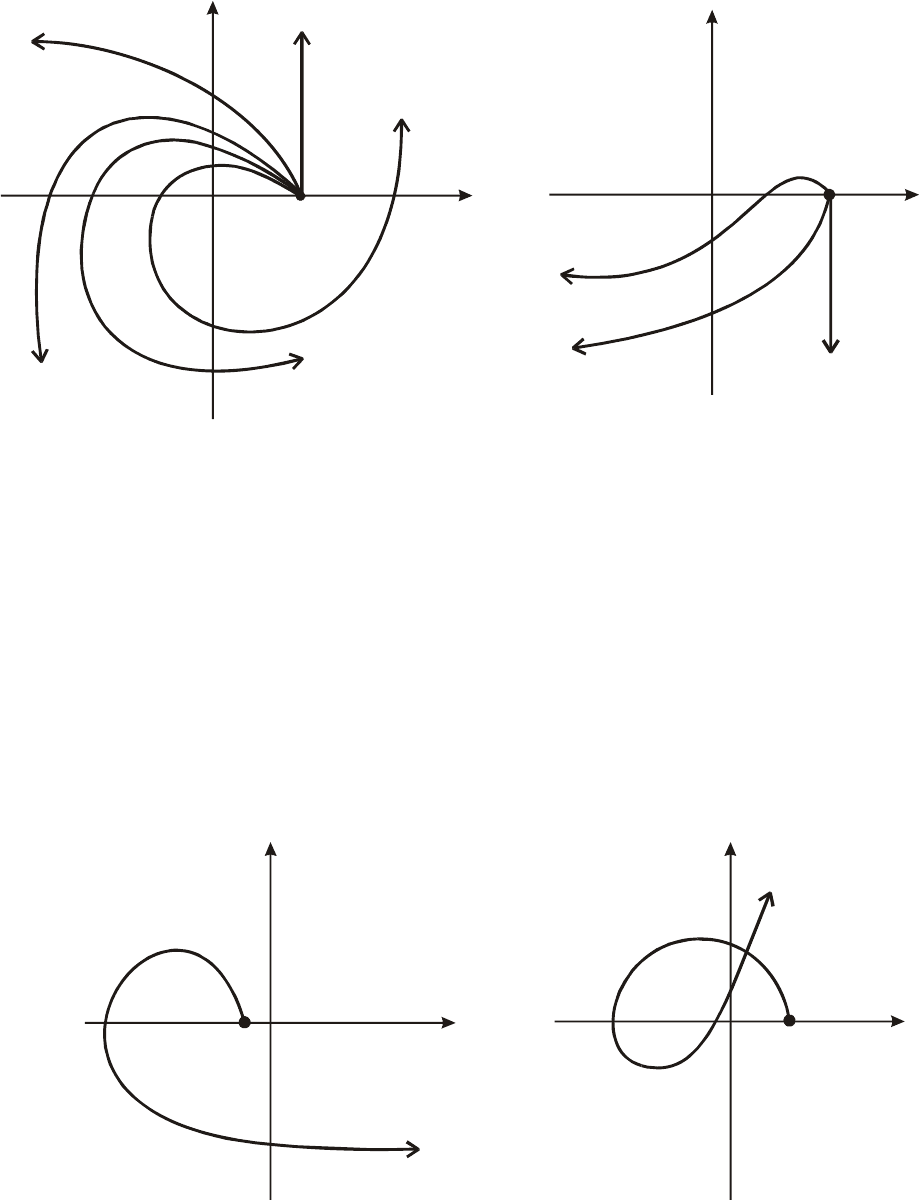
Другими словами, требуется, чтобы при изменении от 0 до
+
∞ годограф, начиная с положительной части вещественной оси,
последовательно проходил квадрантов в положительном направ-
лении (против часовой стрелки) (рис 5. 12).
ω
n
Типичные годографы устойчивых систем, удовлетворяющих
условиям (5. 23), показаны на рис.5.12 для значений
5,,2,1 K
=
n
.
На рис.5.13 – 5.15 показаны годографы неустойчивых систем.
0
X
a
n
n=1
2
3
n=4
n=5
+∞
+∞
ω→+∞
ω=0
+jY
ω→+∞
ω→+∞
.12. Годографы Михайлова устойчивых
систем 1,2,…,5 порядков
n=
n=
ω→
ω→
Рис. 5
0
X
n=1
n=2
n=3
+jY
ω→+∞
ω→+∞
ω→+∞
Рис. 5.13. Годографы Михайлова
неустойчивых систем
1, 2, 3 порядков
ω=0
ω=0
n=5
ω→+∞
ω→+∞
XX
+jY
+jY
0
0
Рис. 5.14. Годограф Михайлова
неустойчивой системы 4-го порядка
(начало во втором квадранте)
Рис. 5.15. Годограф неустойчивой
системы 5-го порядка
(неохват начала координат и 4-го
квадранта)
22
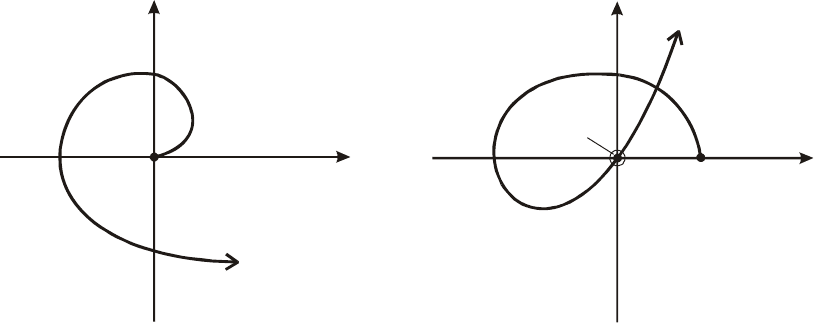
Все они не удовлетворяют условию последовательного охвата
квадрантов в положительном направлении с началом кривой на по-
ложительной части вещественной оси.
n
Рассмотрим кривую Михайлова, когда система находится на
границе устойчивости.
1. Характеристическое уравнение имеет нулевой корень
В случае нулевого корня
)0(
=
n
a
кривая начинается из начала
координат (рис.5.16.а).
2. Характеристическое уравнение имеет пару мнимых
комплексно – сопряженных корней
В случае нахождения на границе пары комплексно – сопря-
женных корней:
01,
ωjp
ii
±
=
+
кривая Михайлова при частоте
0
ωω
=
проходит через начало координат (рис.5.16.б).
0
0
X
X
n=5
n=4
+jY
+jY
ω→+∞
ω→+∞
ω
=0
ω
0
ω
=0
а)
б)
Рис. 5.16. Годографы систем, находящихся на границе устойчивости
3. Вариация коэффициентов характеристического уравнения
На границе устойчивости системы все корни характеристиче-
ского уравнения, кроме
0
ωj
±
, должны находиться в левой полу-
плоскости. В этом случае при малом изменении коэффициентов
характеристического полинома можно добиться перехода мнимых
корней в левую полуплоскость. Этой операции будет соответство-
вать малая деформация кривой Михайлова, после которой кривая
23
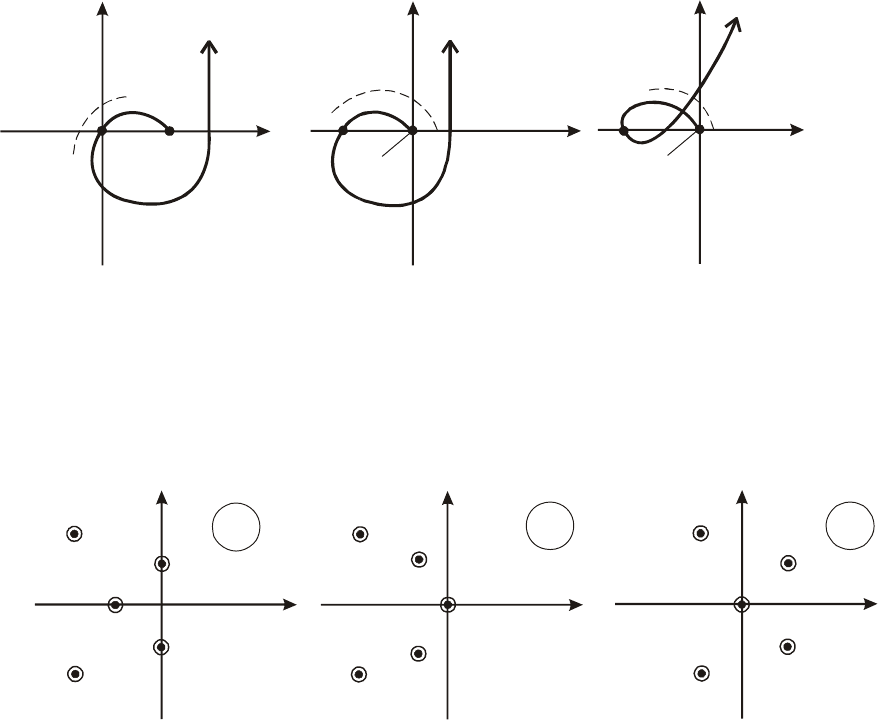
будет последовательно обходить в положительном направлении
квадранты, не проходя через начало координат (рис.5.17.а и
ис.5
озникнуть и при наличии нуле-
ого
полуплоскости, то малое изменение коэффициентов не обеспечит
переход системы в устойчивое состояние (рис.5.17,в и 5.18,в).
чивости Михайлова может быть сформулиро-
ан и
ет ос
ости
равно порядку характеристического полинома n (рис.5.19,а).
р .18.а).
Аналогичная ситуация может в
в корня (рис.5.17.б и рис.5.18.б).
Однако если кроме граничных корней есть и корни в правой
0
X
n=5
0
X
n=5
0
X
n=5
+jY
+jY +jY
ω=
0
ω=
0
ω=
0
б)
а)
в)
ω→+∞
ω→+∞
ω→+∞
Рис. 5.17. Деформация годографа Михайлова системы 5-го порядка при малой
вариации коэффициентов ее характеристического уравнения:
а, б - исходная система находится на границе устойчивости; в - неустойчива
+1
+1
+1
p
+j
+j
+j
а)
б)
в)
p p
Рис. 5.18. Расположение корней исходной системы 5-го порядка
с годографами рис.5.17
Критерий устой
в в другом виде:
В устойчивой системе годограф Михайлова поочередно пере-
сека и координат, начиная с положительной половины оси X
при
0ω =
. Число таких последовательных пересечений в точн
24
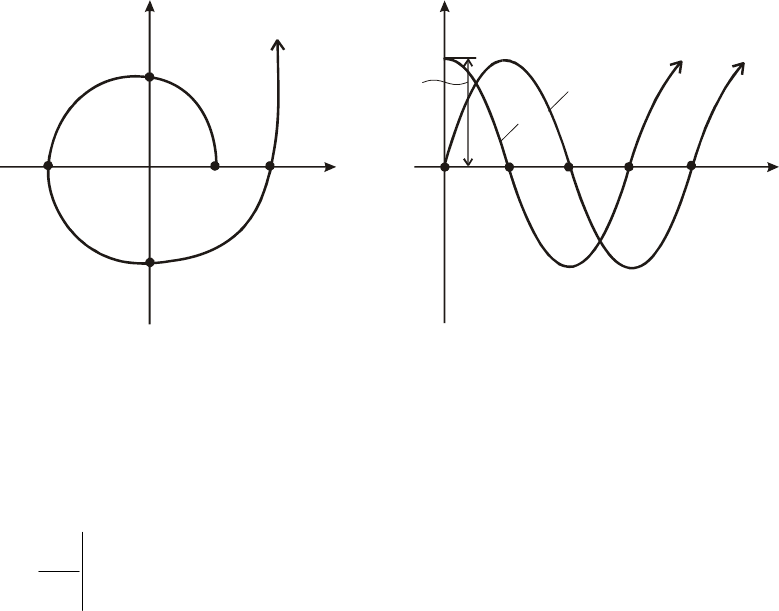
0
0
Y
X
a
n
a
n
X
X,Y
+jY
ω
=0
1
ω
5
ω
5
ω
ω
4
ω
3
ω
2
ω
=0
1
ω→+∞
а)
б)
ω
3
ω
2
ω
4
Рис. 5.19. К альтернативным формулировкам критерия устойчивости Михайлова
Для обеспечения устойчивости необходимо и достаточно вы-
полнение следующих условий:
1.
;
0)0( >=
n
aX
2.
0
ω
0ω
>
=
d
dY
(кривая идет вверх от оси X);
3.
Корни уравнений
0)ω(0)ω(
=
=
Y
и
X
вещественные, положи-
тельные и перемежающиеся (рис. 5.19.б), т. е. между двумя со-
седними действительными (положительными) корнями уравне-
ния
0)ω( =
Y
лежит один действительный (положительный) ко-
рень уравнения
0)ω(
=
X
.
Существование комплексных корней уравнения
0)ω(
=
X
или
0)ω( =
Y
или отсутствие перемежаемости этих корней свиде-
тельствуют о неустойчивости системы.
Заметим, что при повышении порядка системы
)54(
÷
>n
объ-
ем вычислений, связанных с применением критерия Михайлова,
существенно возрастает. В этом случае отдают предпочтение таб-
личному критерию Рауса.
Критерий Найквиста
Этот критерий позволяет судить об устойчивости замкнутой
системы по виду частотной характеристики (годографа) разомкну-
той системы, которая может находиться как аналитически, так и
опытным путем. Последнее обстоятельство сообщает критерию
важное преимущество по сравнению с другими критериями.
25

Рассмотрим критерий Найквиста для нескольких типичных
видов разомкнутых систем.
1. Система, устойчивая в разомкнутом состоянии
Ее передаточная функция имеет вид
1
)1(
)(
)(
)(
1
10
1
10
+++
+++
==
−
−
K
K
nn
mm
scsc
sbsbk
sL
skN
sW
,
причем .
nm <
)(
s
L
– характеристический полином разомкнутой
системы в нормированной форме (
1
=
n
c
).
Образуем вспомогательную функцию
)(
)(
)(
)()(
)(1)(
sL
sD
sL
skNsL
sWsF =
+
=+=
, (5.25)
где – характеристический полином замк-
нутой системы, имеющий, как известно, передаточную функцию
)1()()(
0
+++= kscsD
n
K
)()(
)(
)(1
)(
)(
skNsL
skN
sW
sW
s
+
=
+
=Φ
.
Знаменатель вспомогательной функции (5.25) – характеристи-
ческий полином разомкнутой системы
)(
s
L
, имеющий ту же сте-
пень n, что и характеристический полином замкнутой системы
)(
s
D
.
Поскольку разомкнутая система устойчива, то согласно кри-
терию Михайлова при изменении
ω от 0 до +∞ приращение аргу-
мента
)ω(
j
L
равно
n
2
π
.
Если потребовать устойчивости и замкнутой системы, то, со-
гласно критерию Михайлова, приращение аргумента вектора
)ω(
j
D
при изменении ω от 0 до +∞ будет равно
n
2
π
. Отсюда из
формулы (5.25) следует:
0)ω(arg)ω(arg)ω(arg
=
Δ
−
Δ=Δ
j
L
j
D
j
F
.
26
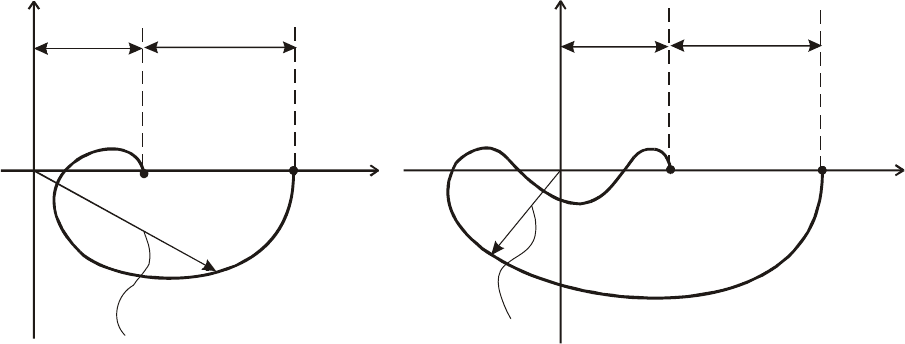
Поэтому годограф вектора
)ω(
j
F
в этом случае не должен охваты-
вать начало координат (рис.5.20. а).
+j
1
k
+1
0
1
k
а)
+1
Fj
()
ω
ω=∞
ω=0
+1
+j
1
k
+1
0
1
k
б)
ω=∞
Fj
()
ω
ω
=0
Рис. 5.20. Годограф вспомогательной функции F j =1+W j для системы,
устойчивой в разомкнутом состоянии
() ()
ωω
Обратим внимание, что при
)ω(0ω
j
F
=
, как видно из фор-
мулы (5.25), равняется
k
+
1
, а
1)(
=
∞
F
.
Если рассматривать годограф частотной характеристики ра-
зомкнутой системы
)ω(
j
W
, то из (5.25) для него имеем:
1)ω()ω(
−
=
j
F
j
W
.
Видим, что
0)(,)0(
=
∞
=
W
k
W
.Следовательно, этот годограф отли-
чается от рассмотренного ранее
)ω(
j
F
только сдвигом влево на (-
1).
Формулировка критерия Найквиста для этого случая гласит:
Для устойчивости замкнутой системы необходимо и доста-
точно, чтобы частотный годограф передаточной функции ра-
зомкнутой системы при изменении
ω от 0 до +∞ не охватывал
точку -1 (рис.5.21).
Обратим внимание, что критерий Найквиста оперирует с го-
дографом передаточной функции разомкнутой системы
)ω(
j
W
, а
не с годографом характеристического полинома замкнутой систе-
мы
)ω(
j
D
(в нормализованной форме) при обращении к критерию
Михайлова.
27
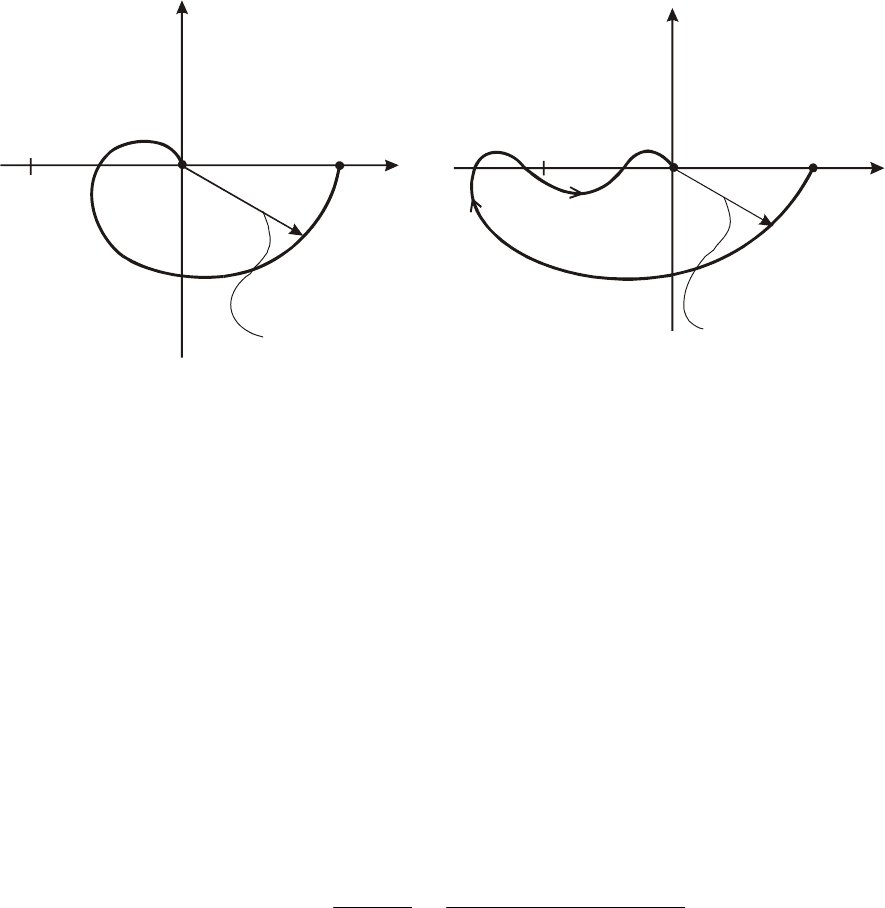
Отметим также, что для графика (рис 5.21,а) увеличение ко-
эффициента усиления
k
может вызвать неустойчивость замкнутой
системы. А для графика рис.5.21,б, наоборот, уменьшение коэффи-
циента усиления
k
может привести замкнутую систему в неустой-
чивое состояние.
+j
+1
0
-1
k
а)
+j
+1
0
-1
k
б)
+
-
W(j )
ω
W(j )
ω
ω=∞
Рис. 5.21. Замкнутая система устойчива: расположение годографа Wj для
системы остающейся после размыкания устойчивой
()
ω
,
2. Система в разомкнутом состоянии находится на границе
устойчивости
2.1. Граница устойчивости апериодическая
Будем полагать, что характеристический полином разомкну-
той системы
)(
s
L
кроме корней в левой полуплоскости имеет и ну-
левые корни – система находится на границе апериодической ус-
тойчивости. Передаточная функция разомкнутой системы в этом
случае имеет вид:
.1;1;
,
)1(
)1(
)(
)(
)(
γ
γ
γ
0
==<
++
++
==
−
mn
n
m
bcnm
scs
sbk
sL
skN
sW
K
K
Такую передаточную функцию имеют астатические системы.
Показатель степени называется порядком астатизма.
γ
28

При обосновании критерия в предыдущем случае предполага-
лось, что корни характеристического полинома
)(
s
L
находятся в
левой полуплоскости вне мнимой оси. Сведем рассматриваемый
случай к предыдущему, сдвинув нулевой корень влево на величину
. Следовательно, разомкнутая система становится устойчивой с
характеристическим полиномом вида:
β
)1()β()(
γ
γ
γ
+++=
−
K
n
scssL
Оценим вид частотного годографа
)ω(
j
W
системы, устремив
сдвиг
β
к нулю. Очевидно,
1)
ν
0β
0ω
β
ω)(lim
k
jW =
≠
→
, где
ν
β
k
– большее положительное число на
вещественной оси;
2)
ν
ωβ
0ωβ,
ω)(
ω)(lim
j
k
jW =
<<
→
, – естественный предел при отсутствии
искусственного параметра
β
.
Точке
0ω
=
рис.5.22 соответствует дуга окружности большо-
го радиуса. Эти три рисунка (а, б и в) относятся к астатическим
системам первого, второго и третьего порядков. На каждом годо-
граф разомкнутой системы не охватывает точку (-1). Следователь-
но, при замыкании все три системы будут устойчивы.
Критерий устойчивости Найквиста для рассматриваемого слу-
чая может иметь такую редакцию:
Для устойчивости замкнутой астатической системы авто-
матического регулирования, которая в разомкнутом состоянии
находится на границе апериодической устойчивости, имея нулевые
корни характеристического полинома, необходимо и достаточно,
чтобы частотный годограф передаточной функции разомкнутой
системы, начиная от точки на действительной оси (при
0ω
=
), не
охватывал точку (-1) при изменении от 0 до +
∞.
ω
29
