Афанасьев А.А. Математические основы теории систем управления
Подождите немного. Документ загружается.

5.6. МАТРИЧНЫЕ КРИТЕРИИ УСТОЙЧИВОСТИ
сти позволяют получить ин-Матричные критерии устойчиво
формации об устойчивости стационарного уравнения состояния
ат
5.6.1. ОБЩИЙ ПРИНЦИП ПОСТРОЕНИЯ МАТРИЧНЫХ КРИТЕРИЕВ
УСТОЙЧИВОСТ
Допустим, на комплексной плоскости
(5.54) на основе специальных тестовых испытаний его м рицы ко-
эффициентов
[]
A
.
И
λ
корней характери-
ения стического уравн матрицы
[
]
A
размерности
n
выбрана неко-
торая область
G
. Это может быть вся левая или не-
которая часть заданной конфигурации.
полуплоскость
Отобразим область
G
с помощью конформного преобразова-
ния на внутренность единичного круга.
Будем полагать, что спектр атрицы
м
[
]
A
целиком находится
внутри области
G
и что существует оператор
H
, который, дейст-
вуя на матрицу
[]
A
, преобразует ее в матрицу
[
]
B
, спектр которой
целиком заключен внутри единичного Принадлежность
пектра матрицы единичному к
Для такой матрицы справедливо тестовое равенство
круга.
с ругу можно легко проверить.
[]
B
[
]
0lim =
∞→
k
k
B
. (5.71)
Действительно, согласно формуле ( .312 ) матрицу и ее сте-
[]
B
пени можно выразить через проекторы
[
]
j
P
и собственные значе-
ния
()
nj
j
,,2,1 K=ρ
:
. (5.72)
Поскольку
[] []
j
k
j
k
PB
∑
=
n
ρ
j
=1
1
<
ρ
j
, то справедливость равенства (5.71) очевид-
а. н
60

5.6.2. ПОСТРОЕНИЕ КРИТЕРИАЛЬНОЙ МАТРИЦЫ ДЛЯ ЛЕВОЙ
[]
B
ПОЛУПЛОСКОСТИ (ОБЛАСТЬ
G
-ЛЕВАЯ СКОСТЬ)
Из теории функций комплек
ПОЛУ
го переменного известно [45],
то с помощью дробно- линейного пре
ПЛО
сно
ч образования
1
1
−ρ
+
ρ
=λ
(5.73)
утр ность круга единичного радиуса с центром в на-
але
можно левую половину комплексной плоскости
λ
конформно ото-
бразить на вн ен
ч координат комплексной плоскости
ρ
.
При таком отображении о разом мнимой оси комплексной
плоскости
λ
будет являться окружность единичного радиуса ком-
плексной плоскости
ρ
, причем точкам мнимой оси
0
б
=
λ
и
j
−
=
λ
будут соответствовать точки окружности
1
−
=
ρ
и
j
=
ρ
.
Подставим в характеристическое уравнение матрицы
[
]
A
[
]
0
=
λ
−
E
(5.74)
A
выражение (5. 73). Полученное уравнение
[]
EA
1
1
−ρ
+ρ
−
после ряда
преобразований [52] примет вид:
[
]
0
=
ρ
−
EB
, (5.75)
где
[]
[
]
{
}
1
2
−
−+= EAEB
. (5.76)
Выражение (5.75) является характеристическим уравнением
ля матрицы
[
]
B
д .
Таким образом, если собственные значения матрицы
[
]
A
при-
надлежат левой полуплоскости
λ
, то собственные значения матри-
цы
[]
B
, определяемые формулой (5.76), заключен утри единич-
ного круга. Если среди собственных
ы вн
значений матрицы
[
]
A
есть
им будут соответствовать собственные значения мат-
представители, расположенные на мнимой оси или в правой полу-
плоскости, то
61

р
[]
B
, расположенные на границе единичного круга или вне
его.
Матричный критерий мптотической устойчивости форму-
ся сле
ицы
аси
лируе дующим образом.
ы (5.76), нахо-
ился единичного круга.
Выполнимость этого условия можно установить по факту
т
внутри
Для асимптотической устойчивости системы (5.54) необхо-
димо и достаточно, чтобы спектр тестовой матрицы
[]
B
, полу-
ченный из матрицы
[]
A
с помощью формул целиком
д
убывания всех элементов матрицы
[
]
k
B
. Возве иден е матрицы в
степень рекомендуется выполнять так, чтобы каждая следующая
м
. (5.77)
но
[]
B
атрица являлась квадратом предыдущей:
[] []
()
K,2,1
2
== mBB
m
k
Опыт показывает, что вычисления мож прекратить, если
модульные значения каждого элемента матрицы
[
]
k
B
не превыша-
ют значения
n1
(n-порядок матрицы
[
]
A
).
Критерий устойчивости можно окончательно сформулировать
в таком виде.
Для о чтобы исходное уравнение состояния (5.54) было
имптотически устойчиво, необходимо и достаточно, чтобы
преобразованная матрица
[]
k
B
стремилась к нулевой матрице пр
∞→
тог
ас
и
k
, где
[]
{
2+= EB
[]
A
}
.
практической реализации этого
еркой выпо
1−
− E
условия можно ограни-При
читься пров лнения неравенства
()
(
ji
n
b
k
ij
,,2,1,
1
K=≤
,
)
n
(5.78)
на все элементы матрицыраспространяемого
[
]
k
B
.
62
5.6.3. ПОСТРОЕНИЕ КРИТЕРИАЛЬНОЙ МАТРИЦЫ
[]
B
ДЛЯ КРУГ
В ЛЕВОЙ ПОЛУПЛОСКОСТИ
А
(ОБЛАСТЬ
G
- ЛЕВОЙ КРУГ В
ПОЛУПЛОСКОСТИ)
Использование критериальной матрицы
[
]
B
для левой полу-
плоскости в форме выражения (5.76) имеет некоторые неудобства,
связанные с наличием трудоемкой процедуры обращения матрицы.
Этот недостаток можно устранить, если вместо левой полуплоско-
ти рассматривать круг радиуса
R
с центром
точке
на вещественной оси с
в [20]. Отобразим этот круг в комплексной плоскости
()
R−
λ
корней характеристического уравнения матрицы
[]
A
на единичный
круг с центром в начале координат комплексной плоскости
ρ
при
помощи функции
R
λ
+
=
ρ
1
. (5.79)
Подставим
()
R1−ρ
=
λ
, нное из формулы (5.79), в характеринайде -
стич
а
еское уравнение (5.74). После несложных преобразований по-
лучим для новой критери льной матрицы
[
]
B
:
[
]
0
=
ρ
−
EB
, (5.80)
где
[
]
[
]
EB RA
+
=
. (5.81)
е числа исходной м ы
[
]
A
Тогда, если все собственны атриц
уравнения состояния (5.54) находятся в
диуса
нутри указанного круга ра-
R
левой полуплоскости, то ма собственные числа трицы
[
]
B
йчивости системы (5.54) фор-
йчивости уравнения состояния
тобы при
принадлежат единичному кругу.
Критерий асимптотической усто
мируется следующим образом:
Для асимптотической усто
(5.54) необходимо и достаточно, ч достаточно большом
радиусе выполнялось условие
R
[] []
{}
0
1
→+=
−
k
k
RAEB
при
∞
→
k
. (5.82)
Круг радиуса в левой полуплоскости (рис. 5.44) должен
быть таких размеров, чтобы вобрать в себя весь спектр устойчивой
R
63
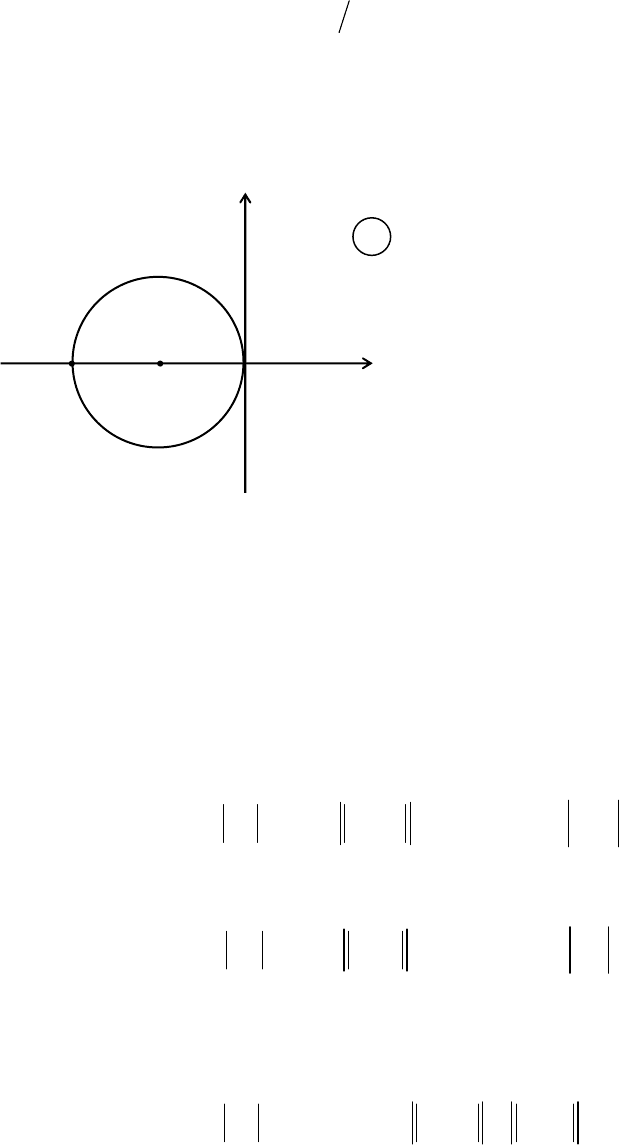
матрицы . Однако выбор чрезмерно большого радиуса
[]
A
R
ведет
двум :
во- , из-за ограниченного числа разрядов ЭВМ некото-
рые матрицы
к опасностям
первых
элементы
[]
RA
будут восприниматься как ,
во- , матрица будет близка к ед
бует числа
нулевые
вторых
увеличения
[]
B
иничной, что потре-
k
для проверки выполнения
Обычно в качестве грани-
неравенства
(5.78).
цы радиуса
R
выбирают его
и котором наблюда-
λ
значение, пр
ется нескольких
ое начальное
значение радиуса
аннулирование
элементов матрицы
[]
1−
RA
.
Приближенн
-2R -R +1
0
+j
] с помощью круга
радиуса
R
, охваты-
вающего весь спектр матрицы
[
]
A
, можно получить, используя
методы локализации собствен-
Рис. 5.44. Локализация собственных чисел
устойчивой матрицы [A
R в левой полуплоскости
ных чисел матрицы, изложенные
неравенств
выше.
В частности, из
Гершгорина (5.52), (5.53) вытекают следующие оценки наибольше-
го по собственного числа матрицы
[
]
A
модулю , не
е нормы
превосходящие
е :
[]
∑
=
=≤λ
n
j
ij
i
aA
1
I
max
max
, (5.83)
[]
∑
=
=≤λ
n
i
ij
j
aA
1
II
max
max
. (5.84)
Из неравенств (5.83), (5.84) получаем оценку Фробе-
ниуса
объединения
[
]
[
]
)
. (5.85)
,(min
III
max
AA≤λ
64
5.6.4. ОЦЕНКА УСТОЙЧИВОСТИ ПО ИТЕРИАЛЬНОЙ МАТРИЦЕ
[]
КР
B
БЕЗ ВОЗВЕДЕНИЯ В СТЕПЕНЬ
Возможны оценки устойчивос
е про-
сравни-
тельно трудоемка.
ка устойчивости по нор
Будем следующие легко вычисляемые нормы:
ти системы по виду матрицы
[]
B
без возведения ее в степень. Актуальность таких (боле
стых) оценок очевидна, т.к. процедура умножения матриц
Оцен мам матрицы
[]
B
рассматривать
[]
∑
=
=
n
j
i
i
bB
I
max
j
, (5.86)
1
[]
∑
=
n
ji
bB
II
max
, (5.87)
=
i
j
1
[]
∑
=
n
ji
ij
bB
,
2
III
, (5.88)
[
]
ji
b
.
ji
nB
,
IV
max=
(5.89)
Для того чтобы исследуемая система была асимпто-
тически устойчива и
(5.54)
[
]
0→
k
B
при
∞
→
k
, достаточно, чтобы
любая из четырех норм рицы мат
[
]
B
(5.86)- (5.89) была меньше
единицы
[
]
1
<
B
. (5.90)
Это неравенство следует из свойств нормы по определению
[]
[
]
[
]
[
]
k
kk
BBBB ≤≤≤
−
K
.
[]
1
[
]
Поэтому если
1<B
, то
0→B
и, следовательно,
k
[
]
0→B
при
∞→
k
k
.
Следует подчеркнуть, что условие (5.90) для устой
ляется достаточным (взятым с запасом).
чивости яв-
65

Если одна из норм матрицы
[
]
B
меньше единицы, то рассмат-
риваемая система является заведомо устойчивой и нет нужды воз-
водить матрицу
[]
B
в степень, реализуя более “тонкий” критерий.
б устойчивости системы должен быть иссле-
дован дополнительно. С этой целью переходим к умножению мат-
рицы
, выстраивая две последовательности:
Если все нормы (5.86) – (5.89) оказываются большими едини-
цы, то из этого не следует, что система является неустойчивой. В
этом случае вопрос о
[]
B
[] []
[
]
4
; BB
82
; B
и т.д.,
[
] []
[
]
842
;; BBB
и т.д.
енты матрицы
[]
k
B
, с некоторого
k
начнут Элем уменьшаться,
ли устойчива Одновременно умень-
атр второй последовательности, так что
при некотором
стремясь к нулю (ес
шаются и нормы м и
система
ц во
).
k
получим:
[
]
1<
k
B
.
Это условие является необходимым и достаточным для су-
ждения об устойчивости си
Таким образом, оценк ти по значению норм мат-
ицы
) или (5.81) строится матрица
стемы.
а устойчивос
р производится в следующей последовательности:
1.
По формулам (5.76
[
]
B
.
. По формулам (5.86) (5.89) вычисля
единицы, то анализируемая
следует присту-
пить к возведению матрицы в степень, последовательно отслежи-
вая
2 ются четыре нормы матрицы
÷
[]
B
. Если одна окажется меньше сис-
тема асимптотически устойчива.
3.
Если все нормы оказались больше единицы, то
нормы матриц
[] []
[
]
[
]
K;
k
B
.
сли при некотором
K ;;;;
842
BBB
норма
[
]
k
B
k
Е стане
дается и рассматриваемую систему следует
считать асимптотически устойчивой.
т меньше единицы, то
условие
[]
0→
k
B
соблю
66
Оценка устойчивости по следу матрицы
След матрицы
рмацию об устойчивости исследуемой системы.
Теорема 5.1
Если при исследовании устойчивости системы (5.54) выпол-
тся неравенство
[]
B
[]
B
[]
∑
=
n
bBSp
(5.91)
=i
ii
1
может дать инфо
няе
[
]
nBSp ≥
, (5.92)
тогда среди собственных чисел
),,2,1( ni
i
K
=
ρ
найдется хотя
ы од справедливо неравенство: б но, для которого
1>
ρ
i
.
Доказательство этой теоремы несложно. Известно
[
]
17
, что
для следа матрицы
[]
k
B
справедливо равенство
[]
k
n
kk
k
BSp ρ++ρ+ρ= K
21
. (5.93)
Из условия теоремы
[]
nBSp
n
i
i
≥ρ=
∑
=1
.
Предположим, что система устойчива, тогда
, (
),,2,1 ni L
=
1
<
ρ
i
,
следовательно,
n
n
i
i
<ρ
∑
=1
,
но
∑∑
==
ρ>ρ
n
i
i
n
i
i
11
.
67

[]
nBSp
n
i
<=ρ
∑
. Поэтому и
i
=1
ницы. Теорема доказана.
образом, если модуль следа матрицы
Следовательно, условие (5.92) будет иметь место только для
неустойчивой системы, для которой модуль хотя одного собствен-
ного числа будет больше еди
[
]
B
Таким равен или
ольше ( - порядок матрицы), т
асимптотически неустойчива.
ва. Требуются дополнительные действия, связан-
ые с
б о исходная система (5.54)
n n
Условие (5.92) является только достаточным для неустойчи-
вости. Если это условие не выполняется, то нельзя утверждать, что
система устойчи
н характером изменения следов матриц
[
]
[
]
[
]
k
BSpBSpBSp K,,
42
.
k
, то
Если начиная с некоторого следы трех оследовательных степе-
система рассматривается как устой-
чивая.
5.6.5. ОЦЕНКА УСТОЙЧИВОСТИ ПО ВЕЛИЧИНЕ НАИБОЛЬШЕГО
ПО МОДУЛЮ СОБСТВЕННОГО ЧИСЛА МАТРИЦЫ
[]
B
Очевидно знание наибольшего по модулю собственного числа
матрицы позволяет однозначно судить б устойчивости исход-
.
Если
п
ней матрицы
[]
k
B
убывают
[]
B
о
ного уравнения состояния
1max
≤
ρ
i
i
, (5.94)
о с
венства в вы-
Максимальное по модулю собственное значение матрицы
3). Будем нумеровать
собственные значения матрицы
т истема асимптотически устойчива при наличии неравенства
и находится на границе устойчивости в случае ра
ражении (5.94).
[]
B
можно определить с помощью формулы (5.9
[
]
B
в порядке убывания их модулей
n
ρ
>
ρ
>ρ K
21
.
68

Получим из (5.93)
[]
k
k
n
k
k
BSp=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎟
⎠
⎞
⎜
⎜
⎛
ρ
ρ
++
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
ρ
ρ
+ρ
11
2
1
1 K
.
⎝
При
∞→
k
имеем
[]
k
k
k
BSp
∞→
=ρ lim
1
.
Следовательно,
[]
k
k
BSp≅ρ
1
, (5.95)
где
k
достаточно велико.
Чтобы избежать извлечения корней высокой степени, можно
вычислить, кроме того, матрицу
[
]
1+k
B
, для которой
[]
11
2
1
1
1
+++
+
ρ++ρ+ρ=
k
n
kk
k
BSp K
.
Сопоставляя это выражение с (5.93), найдем:
[
]
[
]
kk
BSpBSp
1
1
+
≅ρ
. (5.96)
5.7. МАТРИЧНЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ КАЧЕСТВА
СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ НА
ОСНОВЕ ПОСТРОЕНИЯ КРИТЕРИАЛЬНЫХ МАТРИЦ
УСТОЙЧИВОСТИ
[
]
B
ДЛЯ ОБЛАСТЕЙ
матрицу
СПЕЦИАЛЬНОГО ВИДА
До сих пор мы рассматривали критериальную
[
]
B
мат-
,
которая отображает левую корневую полуплоскость исходной
ицы во внутренность единичног
строении аналогичной матрицы
р о круга. Встает вопрос о по-
[]
A
[
]
B
можно
, которая отображала бы на
ных чисел исходной
атри в областях, реализовать необходимы
оцесса, перерегулирова-
еди-
ничный круг области специального вида левой корневой полуплос-
кости матрицы
[]
A
. Локализуя спектр собствен
м е по-цы
[]
A
этих
казатели качества (время переходного пр
69
