Афанасьев А.А. Математические основы теории систем управления
Подождите немного. Документ загружается.

[]
0)(t >x
γ
Если же , то существует последовательность
+∞→
k
t
такая, что
+
∞
=
∞→
)(lim
k
k
tx
причем, стремление к беско-
нечности происходит быс й экспоненты.
ИЯ
Рассмотрим
трее некоторо
6.3. УСЛОВИЕ ОГРАНИЧЕННОСТИ НА ПОЛУОСИ
РЕШЕНИЙ НЕОДНОРОДНОГО УРАВНЕН
уравнение
()
()
[]
() ()
tftxtA
d
t
txd
+=
. (6.26)
Пусть матрица по норме интегрально ограничена
[]
)(tA
()
[]
MdA
t
t
≤
∫
+
ττ
1
,
[
)
∞
∈
,0t
. (6.27)
Пусть выполняется условие (6.27). Для того чтобы уравнение
(6.26) с н льны
Теорема 6.4
ача м условием
(
)
00
=
x
(6.28)
имело ограниченное на полуоси решение при ждой ограниченной
на полуоси функции
ка
(
)
tf
непрерывной , необходимо и достаточно,
чтоб й генеральный показатель уравнения (6.26) был от-
рицателен [15].
6. СТАТОЧНОЕ УСЛОВИЕ АСИМПТОТИЧЕСКОЙ
УСТОЙЧИВОСТИ ОДНОРОДНОГО УРАВНЕНИЯ
Пусть
ы верхни
4. ДО
()
[]
xtA
dt
xd
=
, (6.29)
90
где
()
[]
∞<tASup
и
{
}
m
χ
χ
K,
1
- спектр характеристических по-
казателей системы (6.29), причем
nm
≤
.
Теорема 6.5
Для асимптотической устойчивости линейной однородной
системы (6.29) достаточно [16], чтобы наибольший ее характе-
ристический показатель был бы отрицательным, т.е.
max
<
χ
0
=
χ
k
. (6.30)
я любого решения однородного уравнения (6.29) справед-
ливо неравенство[16]:
Теорема 6.6 (неравенство Важевского)
Дл
()
() () ()
()
∫∫
Λ
tt
dd
x
ττττλ
)
где
≤≤
tt
etxtxet
00
00
, (6.31
()
2
∑
=
j
x
- евклидова норма вектора
j
tx
()
tx
;
()
t
λ
и
(
)
tΛ
- наименьшее и наибольшее собственное число эр-
митово - симметризованной матрицы
()
[]
()
[]
()
[]
{}
At At At
H
=+
∗
1
2
причем
,
(
)
[
]
(
)
[
]
T
tAtA =
∗
;
()
t
λ
и
(
)
tΛ
являются корнями характеристического уравне-
ния
(
)
[
]
{
}
0det =− EtA
H
λ
.
Следствие 1
Для асимптотической устойчивости линейной однородной
системы (6.29) достаточно выполнения условия
при
[
)
∞
∈
,
0
tt
()
0
<
−
≤
Λ ht
,
91
г - положительная постояде h нная.
Следствие
Спектр характеристических показателей линейной системы
целиком распол
2
(6.29) ожен на отрезке
[
]
Ll,
, где
()
t
d
l
t
()
t
d
L
t
t
t
∫
∞→
=
0
mli
ττλ
,
t
t
∫
Λ
=
∞→
0
mli
ττ
.
истемы (6 Для асимптотической устойчивости с .29) доста-
точно
0
<
L
.
6.5. РАСЩЕПЛЕНИЕ РЕШЕНИЙ
ОДНОРОДНОГО УРАВНЕНИЯ ОБЪЕКТА
.1. П НС
Рассмотрим однородное уравнение
6.5 ЛИНЕЙНОЕ РОСТРА ТВО РЕШЕНИЙ
ОДНОРОДНОГО УРАВНЕНИЯ
()
[]
xtA
dt
xd
=
, (6.32)
в котором матрица
()
[
]
tA
сти
n
кусочно разме -непрерывна и ог-
раничена;
рно
∞
<<∞−
t
.
Если
()
tx
- решение уравнения (6.32),
α
- число, то
()
tx
α
-
также решение. Кроме того, сумма двух (или боле шений (6.32)
- также ре ени о множ решений уравнения
инейным пространством, котор у ем обозна-
чать через
tR
. Его размерность равна порядку
n
уравнения (6.32).
Действительно, пусть
()
[]
е) ре
ш е. Поэт му ество векторов
(6.32) является л ое б д
()
(
)
(
)
[
]
txtxtx K=
(6.33)
фундаментальная матрица уравнен
являются линейно-независимые решения уравнения (6.32).
n1
- ия (6.32), столбцами которой
92
(
)
(
)
tRtx
∈
Произвольное решение допускает однозначное
представление
(
)
(
)
[
]
xtxtx
=
, (6.34)
где
[]
T
n
xxxx K
21
,=
- постоянный вектор.
Формулу (6.34) с учетом (6.33) можно записать в эквивалент-
ной форме:
() ()
k
n
k
k
n
n
xtxxt)(xxtxxtxtx
∑
=
=+++=
1
21
)()( K
. (6.35)
21
Таким образом, произвольный вектор
(
)()
tRtx ∈
единствен-
ным образом представляется в виде линейной комбинации ли-
нейно независимых векторов
n
(
)
(
)
nktx
k
K,2,1=
. Очевидно векторы
()
tx
k
образуют базис пространства
(
)
tR
.
Как и в любом линейном пространстве, в
(
)
tR
пространстве
можно выделить подпространства, т.е. множества решений, в свою
я линейными пространствами.
Пусть, например задана совокупность решений
очередь, являющихс
,
()( )
rktx
k
K,2,1=
. Они образуют линейную оболочку
() ()
const,
1=
kk
k
==
∑
k
CCtxtx
линейного пространства
r
(
)
(
)
tRtR ∈
~
размерности
n
r
≤
.
Расщепим пространство
(
)
tR
на прямую сумму подпро-
странств решений, обладающих некоторыми специальными свой-
нествами. Разобьем систему зависимых векторов
()
tx
k
, не меняя их
порядка, на
n
s
≤
групп
BB ,,
1
K
. означим через
()( )
sjtR
j
,...,2,1
Об
S
~
=
линейную оболочку векторов
()
tx
k
j
-й группы,
имеющей размерность
j
n
(в нее линейно - независимых
векторов). При этом всегда справедливо
входит
j
n
:
nn
S
j
j
=
∑
=1
, (6.36)
93
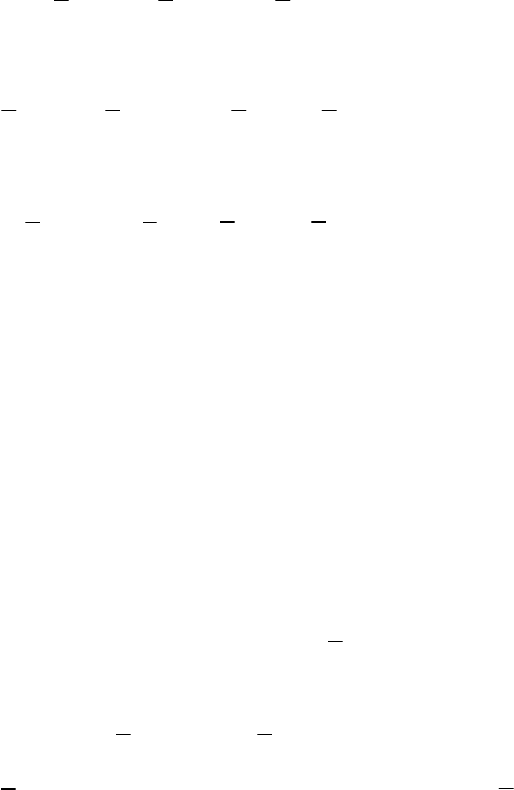
(
)()
(
tRtRtR
S
+++
~
~
~
21
K
)
(
)
tR=
, (6.37)
т ространство
()
tR
расщепляется на прямую сумму подпро-
странств
()
tR
j
.е. п
~
. Следует отметить, что расщепления вида (6.37) оп-
ределяются . Например, для неоднозначно
2
=
n
из равенств
() ()
(
)
tR
2
tRtR
1
~
~
(
)
(
)
(
)
tRtRtR
31
~
~
+=
= +
,
не следует в общем случае, что
(
)
(
)
tRtR
32
~
~
=
.
чки ве во
ак равенство:
В самом деле для линейной оболо кторов справедли
к
()
(
)
(
)
txctxctx
2
2
1
1
+=
,
, напримертак и такое , равенство:
() ()
(
)
(
)
[
]
tx
2
+
,
txctxctx
1
2
1
1
+=
поскольку векторы
()
tx
1
и
(
)
(
)
(
)
txtxtz
21
+=
также образуют фундаментальную матрицу.
6.5.2. ПРОЕКТОРЫ НЕСТАЦИОНАРНОЙ ИСТЕМЫ ЛИНЕЙНЫХ
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Установим связь между произвольным расщеплением про-
условий.
С
странства
()
tR
и численным пространством начальных
Обозначим через
n
R
−
-мерное линейное численное простран-
тво начальных условий. с
Между линейными пространствами
R
и
(
)
tR
существ
имно однозначная связь - каждый вектор
ует вза-
Rx
∈
0
един-
твенное решение
определяет
с
()
(
)
[
]
0
xtxtx
=
()
tx
однозначно определяет вектор
0
x
и каждое решение . Поэтому
прямому разложению (6.37) соответствует прямое разложение про-
транства начальных условий: с
94

S
RRR
~
~
1
++= K
. .38)
Прямое разложение (6.38) порождает полную группу проекто-
ров (матриц проектирования)
(6
[
]
(
)
siP
i
,...1
=
,
обладающих свойствами:
[] [] []
[
]
(
)
iPPPP
jiii
== 0,
2
,
[]
EP
s
i
i
=
∑
=1
. )
Если произвольны
j≠
(6.39
й постоянный вектор
i
Rx
~
0
∈
, то справедливо
[
]
00
xxP
i
=
. (6.40)
Аналогичное равенство имеет место и для произвольного решения
()
Rtx
i
()
t
~
∈
:
(
)
[
]
(
)
(
)
txtxtP
i
=
. (6.41)
Найдем выражение для матрицы проектирования . Учи-
тывая (6.40), имеем:
()
[]
i
tP
()
(
)
[
]
(
)
[
]
[
]
00
xPtxxtx
i
xt
=
=
.
Принимая во внимание, что
(
)
[
]
(
)
txtxx
1
0
=
,
получим:
−
()
(
)
[
]
[
]
(
)
[
]
(
)
xt
1−
txPtxtx
i
=
.
Сравнивая это выражение с формулой (6.41), найдем:
()
[]
(
)
[
]
[
]
(
)
[
]
1−
= txPtxtP
i
i
. (6.42)
Из зависимостей (6.39), (6.42) следуют соотношения:
, (6.43)
()
[]
()
[][]
()
[]
EtxPtxtP
i
i
i
i
==
∑∑
=
−
= 1
1
1
ss
()
[]
()
[][]
(
)
[
]
(
)
[
]
[
]
(
)
[
]
()
[]
i
ii
i
tPtxPtxtxPtxtP ===
2 −− 112
, (6.44)
()
[]
()
[
]
(
)
[]
[
]
[
]
(
)
[
]
0
1
==
−
txPPtxtPtP
ji
ji
. (6.45)
95
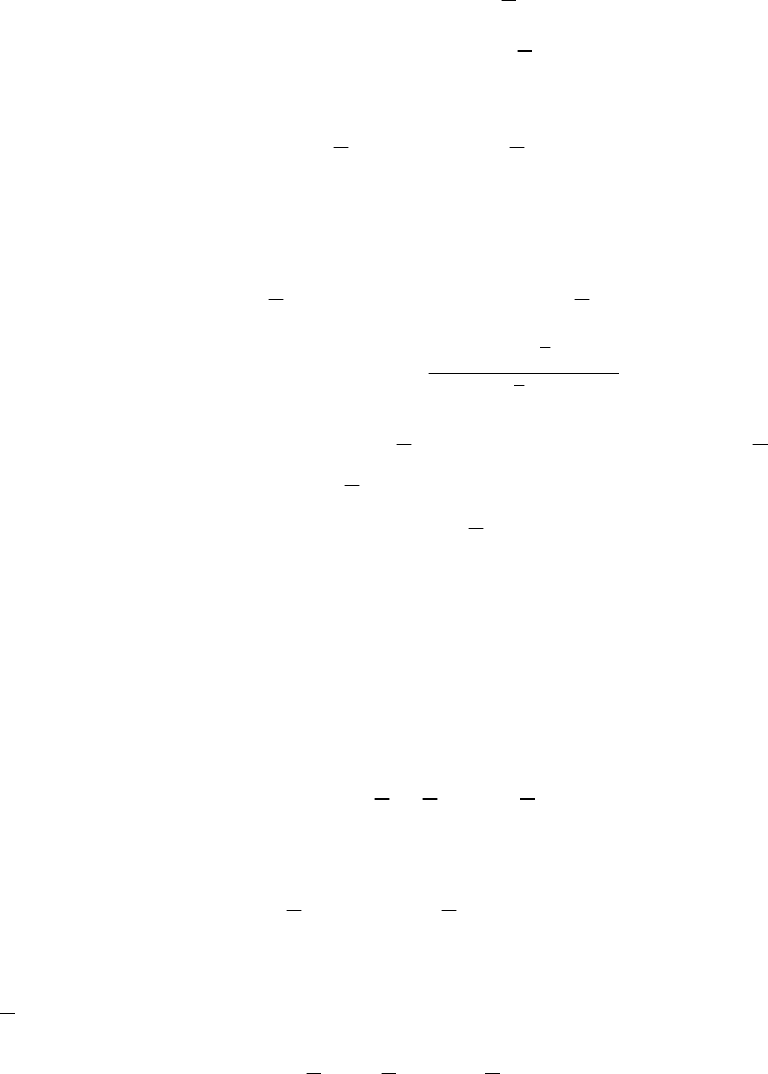
Формулы (6.43) - (6.45) подтверждают, что матрицы яв-
если -
()
[]
i
tP
свойстваляются матрицами проектирования, аналогичными
ми обладают постоянные матрицы
[
]
i
P
.
Матрицы называются матрицами проектирования
ешения однородного уравнения (6.32) на подпро
()
[]
i
tP
р странства
()
tR
i
~
.
()
tR
i
~
(
)
t
на подпростран
x
ство ы спроектировать векЧтоб тор ,
т.е. получить независимое решение
(
)
tx
i
, необходимо
ваться формулой
воспользо-
()
(
)
[
]
(
)
txtPtx
i
i
=
, (6.46)
которая в развернутом виде имеет очевидный геометрический
смысл:
() ()
[]
[
]
(
)
[
]
(
)
i
x
x
0
0
i
i
txPtxtx
421
−
=
Умножая слева вектор
tx
1
43
. (6.47)
в (6.47) на матрицу
()
[
]
1−
tx
(
)
tx
, полу-
аем начальный вектор
0
x
t к мо-ч , т.е. возвращаемся от момента
менту . Полученный вектор
0
x
0=
t
проектируем на подпростран-
ство
i
R
~
с помощью проектора
[
]
i
P
. Затем от момента
0=
t
возвр
аемся к моменту t с помощью умножения слева на матрицу
()
[]
tx
.
а-
щ
Формула (6.42) для проекторов
(
)
[
]
i
tP
может быть легко полу-
ена линейно - незавч и другим путем. Возьмем произвольные иси-
мые векторы
n
xxx
0
2
0
1
0
,,, K
и уравнения (6.32) найдем соответствующее решение однородного
()
(
)
[]
(
)
nixtxtx
ii
K,1
0
==
. (6.48)
Образуем матрицу , столбцами которой являются векторы
()
[]
tT
()
tx
i
()
[]
[
()
(
)
(
)
]
[
(
)
]
[
]
Ttxtxtx
n
=K
2
,
, (6.49)
txtT =
1
96
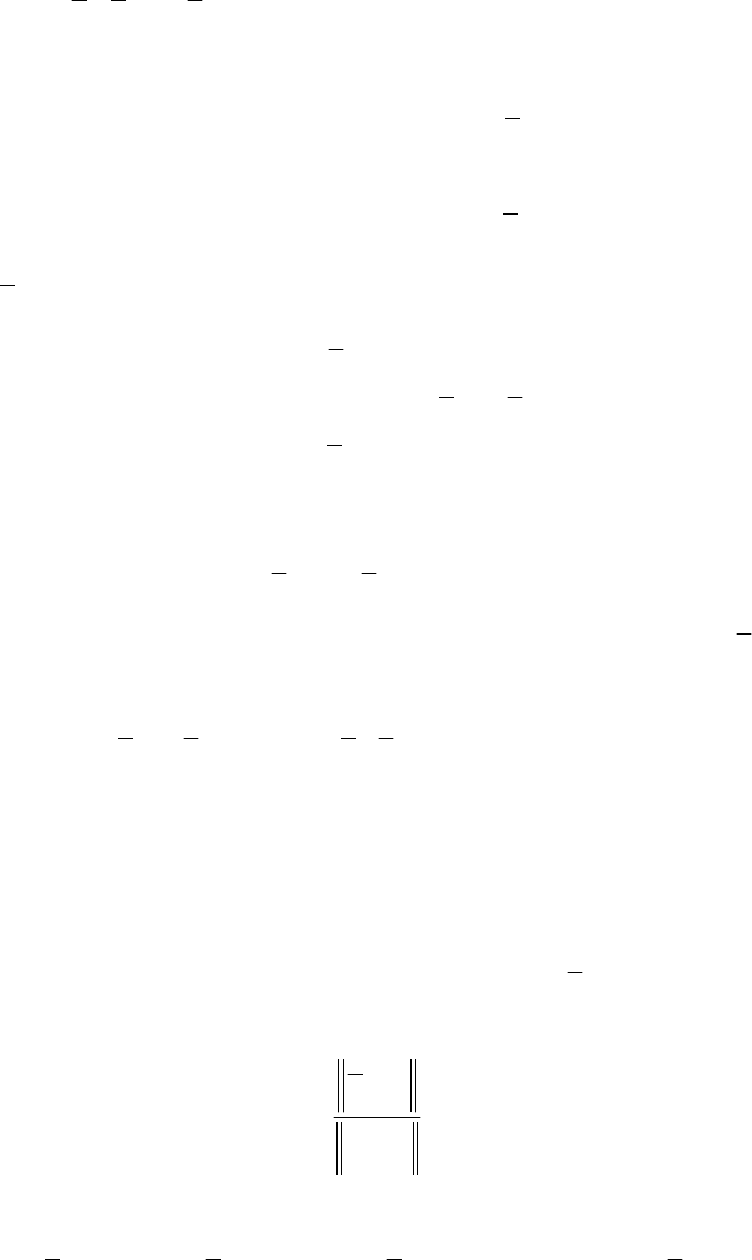
[]
[
]
n
xxxT
0
2
0
1
0
K=
где .
Найдем матрицу, обратную матрице
(
)
[
]
tT
()
[] []
()
[]
(
)
()
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
==
−−−
ty
ty
txTtT
n
M
1
111
, (6.50)
где
()
ty
i
- i-я стро атрицы
()
ка м
[
]
Tt
−1
. Тогда очевидно
[]
()
0,
0
1
0
y
⎤⎡
0
n
y
⎥
⎦
⎢
⎣
о следует
1
ii
yyT =
⎥
⎥
⎢
⎢
=
−
M
(эт из равенства (6.50), взятого для , т. к.
()
[]
Ex
=
0
0
=
t
),
(
)
(
)
[
]
1
0
−
= txyty
ii
. (6.51)
(
)
[]
(
)
tx
i
i
tP
, соответствующих векторам Для проекторов , по-
формулу:
лучим с учетом выражений (6.48), (6.51)
()
[]
() ()
(
)
[
]
(
)
[
]
(
)
[
][ ]
()
[]
11
00
−−
=== txPtxtxyxtxtytxtP
i
iiii
i
. (6.52)
МЫ
ИЯ
В соответствии с формулой (6.22) для
6.5.3. ГЕНЕРАЛЬНЫЕ ПОКАЗАТЕЛИ ГРУПП НЕЗАВИСИ Х
РЕШЕНИЙ НЕСТАЦИОНАРНОГО ОДНОРОДНОГО УРАВНЕНИЯ
СОСТОЯН
()
),,1( sitx
i
K=
ре-
шения будет справедливо неравенство
() ()
τ
−
α
α
τβ
β
τ
−
≤≤
t
i
i
t
i
i
i
i
eN
x
tx
eN
)(
)(
, (6.53)
где
[]
[
]
[
]
[
]
[
]
[
]
)()()()()()(
1
ττ
iiii
xxPtxxPtxxtxtx
−
===
.
00
ii
Введем обозначение
97
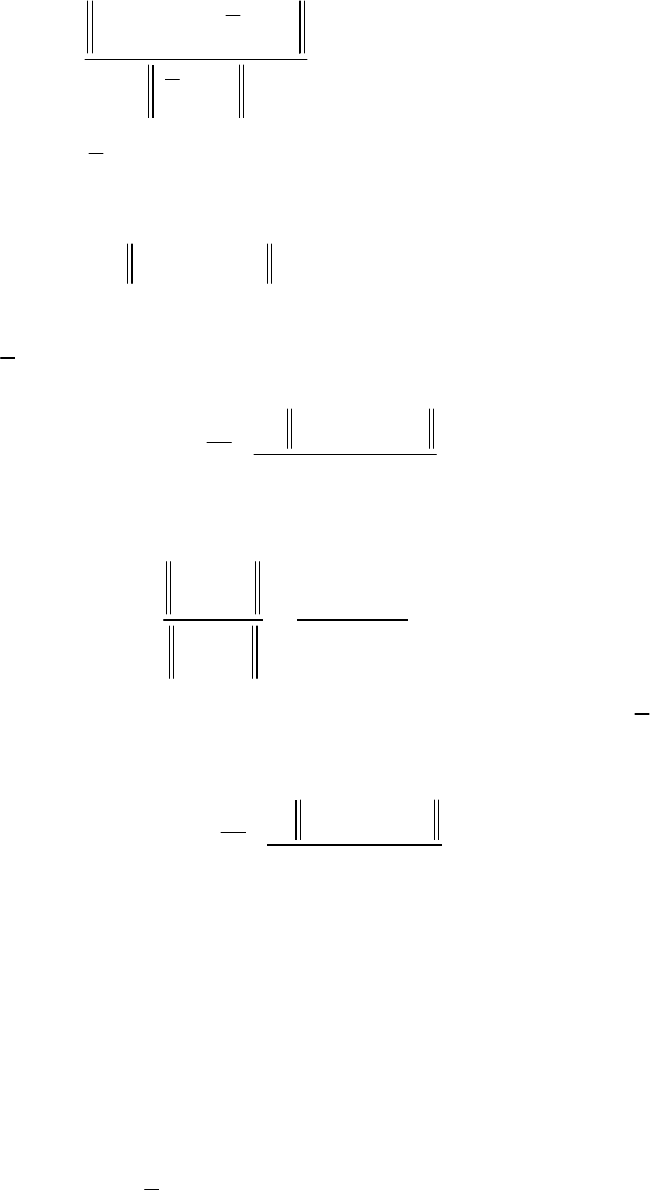
()
[]
(
)
[
]
[
]
(
)
[
]
, τ=τ xPtxtH
i
i
1−
- Коши для i - й группы независимых решений.
Тогда и
матрица
меем из (6.53)
()
[
]
(
)
()
()
τ
ττ
−t
i
i
xtH
,
Поскольку вектор
α
α
τ
≤
i
i
i
eN
x
.
()
τ
i
x
произвольный, то можем его выбрать рав-
ным единичным. В этом случае
()
[]
(
)
τα
α
τ
−
≤
t
i
i
i
eNtH ,
.
следует выражение для верхнего генеральногоОтсюда показателя
решения
()
tx
i
i
α
(
)
[
]
τ
τ
α
τ
−
=
∞→−
t
tH
i
t
i
,ln
mli
. (6.54)
Учитывая, что из (6.53) имеем
()
()
()
i
N
tx
i
β
нахождение нижнего ого показателя решения
i
e
x
t
i
τβ
τ
−−
≤
,
генеральн
()
tx
i
мо-
жем свести к предыдущему случаю:
(
)
[
]
τ
τ
β
τ
−
−=
∞→−
t
t,ln H
i
t
i
mli
, (6.55)
где
[]
(
[
)
]
[
]
(
)
[
]
1
),(
−
τ=τ txPxtH
i
i
.
улы показа-
тели (верхние и нижние) i-й группы независимых решений совпа-
д
ши:
Форм (6.54), (6.55) показывают, что генеральные
ают с генеральными показателями соответствующих матриц Ко-
()
(
)
[
]
i
i
i
ttx α=τδ=δ ,][ H
, (6.56)
98
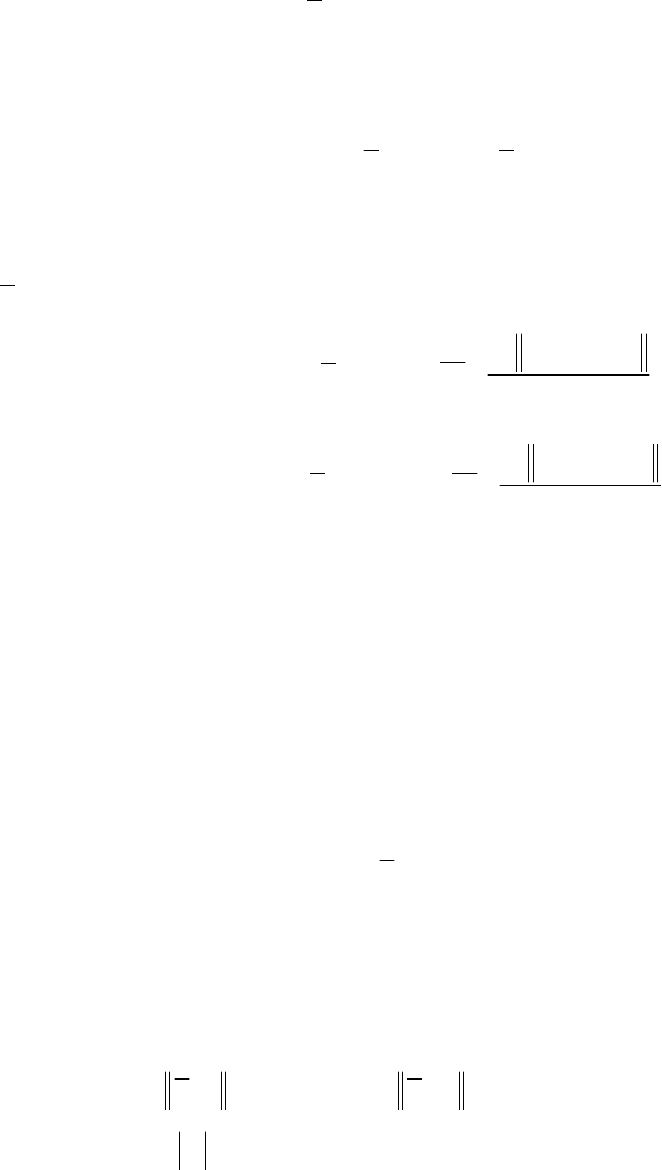
(
)
(
)
[
]
i
β
. (6.56)
i
i
ttx =τδ−=γ ,][ H
Для существования интервалов регулярности необходимо,
чтобы
(
)
(
)
][][
1ii
txtx
ii
+
γ<δ
.
Если , то формулы (6.54), (6.55) позволяют найти вы-
ажения генеральных показателей про
[]
EP
i
=
для р извольного решения
()
tx
:
()
[]
(
)
[
]
τ
τ
δα
τ
−
==
∞→−
t
tH
tx
t
,ln
mli
, (6.58)
()
[]
(
)
[
]
τ
τ
γβ
τ
−
t
t,
−==
∞→−
H
tx
t
ln
mli
торы образуют полную группу), легко получить выраже-
ние для матрицы Коши через ее проекции
. (6.60)
Для асимптотической устойчивости произвольного решения
уравнения (6.32) необходимо и достаточно, чтобы верхний гене-
ральный показатель
. (6.59)
Принимая во внимание формулы (6.39) (они показывают, что
проек
[]
i
P
()
[]
()
[]
∑
=
=
S
i
i
tHtH
1
,,
ττ
(
)
[
]
tx
δ
α
=
, определяемый по формуле (6.58),
был отрицателен:
0
<
α
.
В этом случае все решения уравнения (6.32) удовлетворяют
оценке вида
(
)
(
)
(
)
τ
τ
ν
xeNtx
t
−
−
≤
,
+∞
<
≤
<
∞
−
t
τ
, (6.61)
где N и
α
ν
=
- положительные постоянные.
6.5.4. ГЕНЕРАЛЬНЫЕ ПОКАЗАТЕЛИ СМЕЩЕННОГО УРАВНЕНИЯ
СОСТОЯНИЯ
Смещенное уравнение состояния имеет вид
99
