Афанасьев А.А. Математические основы теории систем управления
Подождите немного. Документ загружается.


()
[]
{}
zEtA
d
t
zd
(6.62)
где
σ
−=
,
σ
- скалярный, в общем случае комплексный, параметр.
: Решения уравнений (6.32) и (6.62) тесно связаны
()
(
)
t
etxtz
σ
−
=
, (6.63)
()
[]
(
)
[
]
(
)
τ
σ
τστ
−
−
=
t
tHtH ,,, e
, (6.64)
де
()
[]
σ
τ
,,tH
г - матрица Коши смещенн
) следуют выражения для генеральных
ешений:
ого уравнения.
Из формул (6.63), (6.64
показателей произвольных р
()
[]
[
(
)
]
Re
−
δ
δ
σ
= tx
, (6.65)
tz
()
[]
[
(
)
]
Re
−
γ
γ
σ
= tx
. (6.66)
раведливы и для независимых реше-
tz
Аналогичные выражения сп
ний.
100
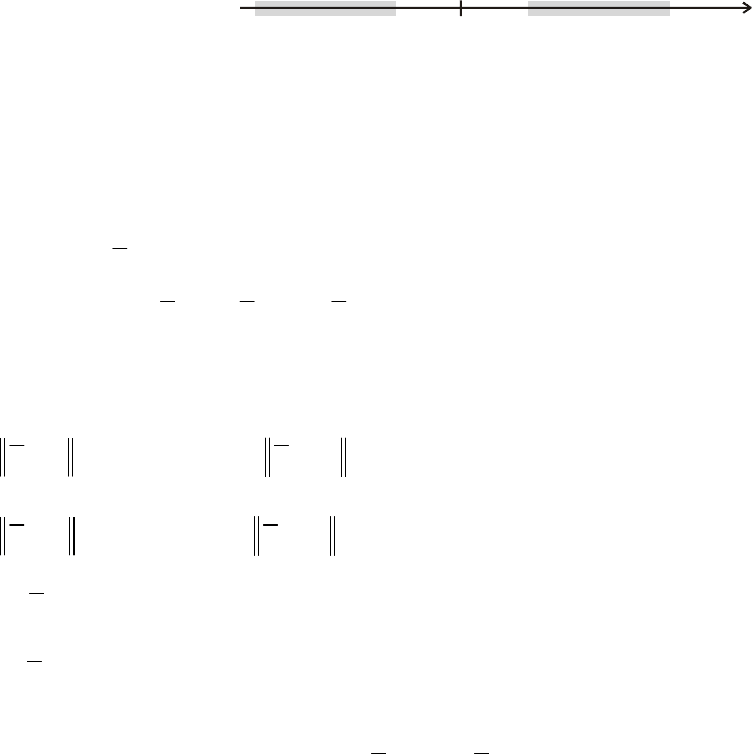
6.5.5. ЭКСПОНЕНЦИАЛЬНАЯ ДИХОТОМИЯ РЕШЕНИЙ
(РАСЩЕПЛЕНИЕ РЕШЕНИЙ НА ДВА)
Будем говорить, что линейное пространство решений
уравнения (6.32) допускает экспоненциально - дихотомическое
расщепление на оси генеральных показателей, если расщепля-
ется в прямую сумму подпространств
()
tR
()
tR
(
)
tR
1
~
,
(
)
tR
2
~
:
(
)
(
)
(
)
tRtRtR
21
~
~
+=
, (6.67)
причем верхний генераль-
ный показатель подпро-
странства
(
)
tR
1
~
отрицате-
лен, а ниж ген ль
показател
()
ний
ера ный
ь подпространст-
ва
tR
2
~
положителен (рис.
6.4).
иеКаждое решен
()
(
)
tRtx
∈
состоит из суммы двух решений:
(
)
(
)
(
)
txtxtx
21
+
=
, (6.68)
причем существуют положительные постоянные
2121
,,,
ν
ν
NN
, та-
ие, что к
()
(
)
(
)
τ
τν
1
11
1
xeNtx
t−−
≤
, (6.69)
()
(
)
(
)
τ≥
τ−ν
2
22
2
xeNtx
t
,
+∞<
≤
<
∞
−
t
τ
. (6.70)
()
[
]
0
11
<
−
=
=
ν
δ
δ
tx
, (6.71)
()
[
]
0
222
>
=
=
ν
γ
γ
tx
. (6.72)
Неравенствам (6.69), (6.70) будет соответствовать характер
зменения во времени норм решений
и
(
)
tx
1
и
()
tx
2
, показанный на
рис. 6.5.
Пусть
21
~
~
R
RR +=
[ ]
γ δ
2
2
[ ]
γ δ
1 1
σ
Рис. 6.4. Интервалы генеральных пок тел
дихотомического расщепления реш й
0
аза ей
ени
однородного уравнения состояния
с нестационарной матрицей
(6.32)
101
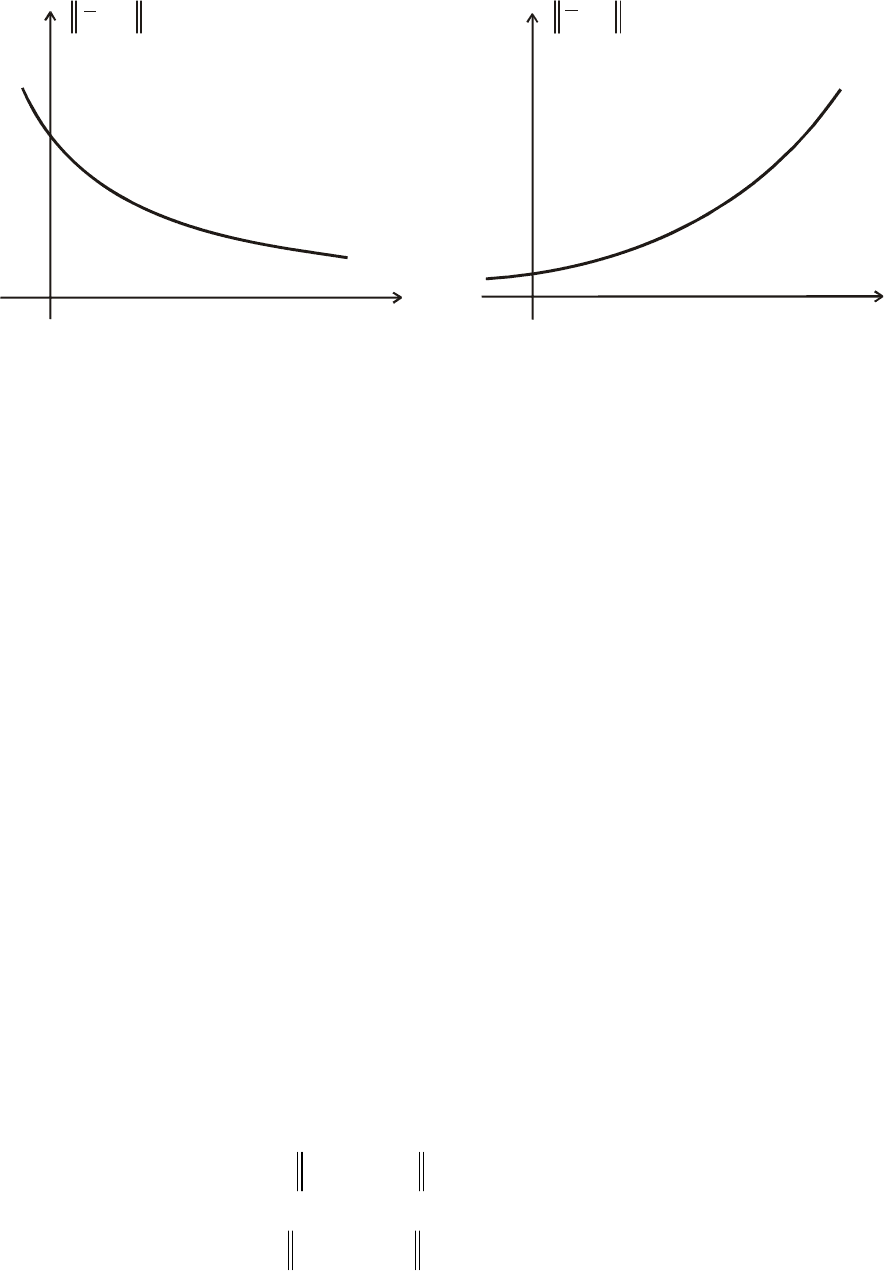
соответствующее начальных условий для начального
момента и , - матрицы проектирования на
расщепление
0
0
=t
[]
1
P
[]
2
P
1
~
R
и
2
~
R
.
Причем
[] []
1
2
1
PP =
;
[
][]
2
2
2
PP =
;
[
]
[
]
0
2
1
=PP
;
[
]
[
]
EPP =+
.
2
1
Тогда матрицы
()
[]
(
)
[]
[
]
(
)
[
]
1
1
−
= txP
1
txtP
()
, (6.73)
[
]
(
)
][
[
]
(
)
[
]
1
2
−
txPt
2
= xtP
матрицами проектирован
Для матриц Коши
, (6.74)
являются ия в пространстве .
()
tR
()
[]
)(
(
)
[
]
[
]
()
(
)
[
]
1
21
,
−
=
ττ
xPtxtH
21
(6.75)
имеем
()
[]
0,
1
1
<δ=τδ tH
,
(
)
[
]
0,
2
2
<
γ
−
=
τ
δ
tH
,
т.
е.
()
[]
(
)
τν
τ
−−
≤
t
eNtH
1
1
1
,
, (6.76)
()
[]
(
)
τν
τ
−−
≤
t
eNtH
2
2
2
,
, (6.77)
+
∞
<
≤<∞−
t
τ
.
t
а)
б)
t
0
0
рм р
епл
Рис. 6.5. Характер изменения во времени но ешений, принадлежащих
дихотомическому расщ ению
x
1
()
t
x
(
t
2
)
102
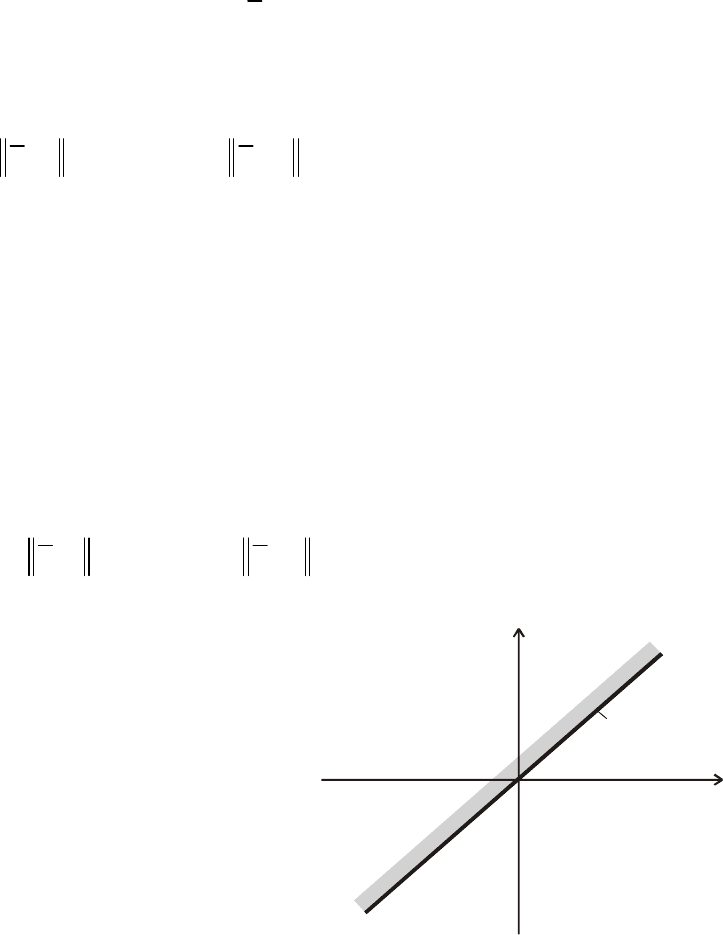
Отметим два важных частных случая:
1)
Верхний генера
льный показатель
δ
уравнения (6.32) отрицате-
лен
(
)
[
]
0
<
δ
tx
.
В этом случае все решения уравнения (6.32) удовлетворяют оцен-
вида ке
(
)
,)()(
τ
τ
ν
xeNtx
t
−
−
≤
+∞<
≤
<
∞
−
t
τ
,
1
R
со-
ν
,
N
где - по пространство
сов тво
стоит из нулевого вектора
ложительные постоянные. Под
падает со всем пространством
R
. Подпространс
2
R
[
]
EP
=
1
,
[
]
2
P 0
=
.
Уравнение (6.32) асимптотически устойчиво при
t
→∞
.
2)
Нижний генеральный показатель
γ
положителен. В этом случае
все решения удовлетворяют оценке
()
(
)
(
)
,
τ
τ
ν
xeNtx
t
−
>
−
∞
<
≤
<
+∞
τ
t
,
где
ν
,
N
- положительные п -о
стоянные Подпространство
t
.
R
2
совпадает со всем пространст-
вом
R
, а подпространство
1
R
t=
τ
состоит из нулевого вектора
[]
0
1
=P
,
[]
EP =
2
и этом все р
я (6.32) эк
возрастают при
0
τ
t
τ
≥
.
Пр ешения уравне-
ни споненциально
∞
→
t
. Урав-
лностью неус-нение (6.32) по
тойчиво.
Рис. 6.6. Область определения
матрицы Коши
103

Обратим внимание, что матрица Коши является функцией
двух переменных
+
∞
<
≤
<∞−
t
τ
. (6.78)
Из неравенства (6.78) следует, что областью определения мат-
ицы Коши является полуплоскость, рр асположенная выше прямой
t
=τ
(рис. 6.6).
ОНЕНЦИАЛЬНАЯ ДИХОТОМИЯ
енциальной дихотомичности уравнения
6.5.6. ЭКСП
СТАЦИОНАРНОГО ОБЪЕКТА
Для экспон
[]
xA
dt
xd
=
(6.79)
с постоянной матрицей необходимо и достаточно, чтобы
вещественной частью,
дихотомично, то, как
на всей временной оси (если
ремится к бесконечности при
[]
A
матрица
[]
A
не имела собственных чисел с
равной нулю.
с Е ли решение однородного уравнения
показано выше, оно не ограничено
решение устойчиво, то оно ст
−∞→
t
).
При наличии мнимого собственного
нение (6.79) имеет одно ограниченн
()
[]
,
1
числа матрицы урав-
ое независимое решение:
[]
A
0
max
<
α
=
τδ tH
()
[]
,
2
, (6.80)
=
τ
γ
tH
где
0
min
>
α
, (6.81)
λ
α
Re
max
=
- вещественная часть ближайшего к мнимой оси
собственного числа матрицы
[
]
A
, лежащего в ле-
вой полуплоскости;
λ
α
Re
min
=
- вещественная часть ближайшего к мнимой оси
собственного числа матрицы
[
]
A
, лежащего в
правой полуплоскости.
104
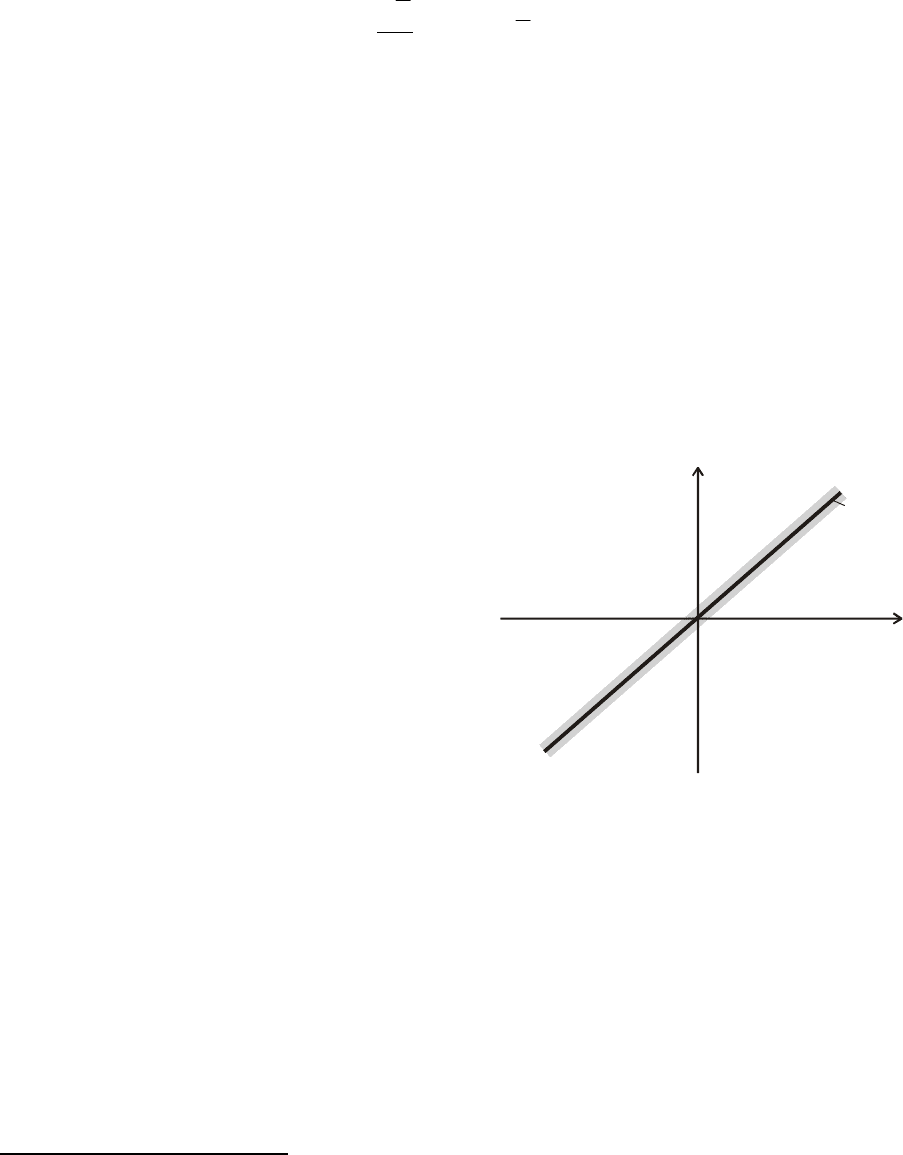
6.5.7. ФУНКЦИЯ ГРИНА ЭКСП ЦИАЛЬНОГО
я од
ОНЕН ОБЪЕКТА
Дл нородного уравнения объекта
()
[]
xtA
d
t
xd
=
(6.82)
имеем
[]
1
P
и
[
]
2
P
- проекторы, определяющие экспоненциальную
дихотомию решений.
Матрицы Коши (6.75) по норме
.76), (6.77).
Матрицу
,
удовлетворяют оценкам
(6
+∞<<
()
[]
()
[]
()
[]
⎨
⎧
τ<τ−
ττ
=τ
ttH
>ttH
tG
при,
при,
,
1
∞
−
t
,
τ
(6.83)
⎩
2
бу ывать главной функцией Грина .
1.
На плоскости
дем наз
2
Рассмотрим свойства функ-
ции Грина:
t
0
Рис. 6.7. Область определения
t=
τ
τ
[(
τ
,
t
(рис. 6.7)
области выше прямой
)
,
τ
]=[( )]
Gt Ht,
τ
1
[( )]=[( )]
Gt, Ht,
ττ
2
−
(< )
t
τ
(> )
t
τ
функция Грина совпадает с
первым выражением (6.83) в
τ
=
t
, -
со вторым выражением (6.83)
в области ниже прямой
τ
=
t
.
На самой прямой
τ
=
t
функ-
ция Грина не определена, т.к.
она терпит на этой прямой
разрыв, причем
)
]
()
[]
функции Грина
(
[
(
)
[
]
[
]
(
)
[
]
(
)
[
][ ]
()
[]
0,0
1
2
1
1
txPtxtxPtxttG +=+−−
−−
()
[ ][] []
{}
()
[]
()
[]
()
[]
,
11
21
txtxtxPPtx
ttG
==+
=
−−
.E
(6.84)
Аналогично
()
][
(
)
[
]
EttGttG
−
=
−
−
+
0,0,
.
2
Для главной функции Грина проекторы
[
]
P
12()
задают дихотомию решения (6.82)
ппу. и образуют полную гру
105

2. Функция Грина ограничена, удовлетворяя оценке
[]
τν
τ
−−
≤
t
eNtG ),(
<
<
∞
−
t
,
τ
+
∞
, , (6.85)
где
ν
,
N
- положительные постоянные.
Ограниченность следует из задания функции формулами
(6.83).
3. и всех
τ
≠
t
Пр функция Грина удовлетворяет дифференциаль-
ным уравнениям:
[]
()
[][]
GtA
G
=
t
∂
∂
, (6.86)
[]
[]
()
[]
tAG
G
−=
∂
τ
∂
, (6.87)
(6.83).
) Есл
которые получаются при непосредственном дифференцировании
4 и верхний генеральный показатель уравнения (6.82) отрица-
телен
(
)
[]
0,
<
τ
δ tH
,
что соответствует устойчивому уравнению (6.82), то
[]
[
]
0,
21
=
= PEP
и выражение для функции Грина имеет вид
()
[]
(
)
[
]
⎧
,,,
⎩
⎨
<
=
.,0
,
τ
τ
τ
τ
t
tG
(6.8
t>tH
8)
В этом случае (объект экспоненциально дихотомичен и устой-
чив) функция Грина совпадает с весовой (импульсной) функцией
()
[]
,,
τ
tU
задающей решение неоднородного уравнения
3
()
[]
()
tfytA
d
t
yd
+=
(6.89)
в следующем виде:
3
Весовая функция - оригинал передаточной функции, является решением
матричного уравнения
()
[
]
()
[]
()
[]
()
∂τ
∂
τδ
Ut
t
At U t E t
,
,=+
.
τ−
106

() ( )
[]
() ( )
[]
()
dssfstUytUty
t
∫
+=
τ
ττ
,,
. (6.90)
Если нижний генеральный показатель уравнения (6.82) положи-
телен (уравнение неустойчиво)
(
)
[
]
0, >
τ
γ
tH
,
то
[
]
[
]
EPP
=
=
21
,0
и для функции Грина имеем выражение
()
[]
()
[]
⎩
⎨
⎧
<−
=
.,,
,,0
,
ττ
τ
τ
ttH
t>
tG
6.5.8. УСТАНОВИВШИЙСЯ РЕЖИМ ДВИЖЕНИЯ РЕГУЛЯРНОГО
ОБЪЕКТА
(6.89). Рассмотрим неоднородное уравнение объекта Его ре-
шение
()
ty
будем считать установившимся, если оно аничено на
временной оси
огр
()
+
∞
<
<
∞
−
=
< tcty ,const
.
Объект (6.89) будем называть регулярным, если для любого
ограниченного входного сигнала
()
+∞<<∞−=< tdtf ,const
(6.91)
уравнение (6.89) имеет единственное установившееся решение.
Объект (6.89) будем называть нерегулярным, если хотя бы
ля одного ограниченного входного сигнала
т установившегося решения.
Теорем
объекта (6.89) необходимо и достаточно,
чтобы однородное уравнение, соответствующее (6.89) было экс-
поненциально дихотомическим
д уравнение (6.89) не име-
е
а 6.7
Для регулярности
[
]
44
.
107

1. Рассмотрим выражение
4
() ( )
[]
()
∫
+∞
=
τττ
dftGty ,
, (6.92)
∞−
которое в развернутом виде можно записать:
() ( )
[]
() ( )
[]
()
∫∫
+∞
−=
t
dftHdftHty
ττττττ
1
,,
. (6.93)
∞− t
Принимая во внимание оценки (6.85), (6.91), из (6.93) можем полу-
чить неравенство
2
()
() ()
ν
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
τ+τ≤
∫∫
∞+
−τν−
∞−
τ−ν−
dN
dededNty
t
t
t
t
2
. (6.94)
Следовательно, функция (6.92) ограничена
()
const
=
≤
Cty
.
(
)
ty
Дифференцируя (6.93) по t, получим [15], что удовлетво-
яет неоднородному уравнению (6.89), т.е
м, выраже дает о-
вившееся решение.
.
В частном случае, когда уравне
р . функция (6.93) является
решением уравнения (6.89).
Таким образо ние (6.93) единственное устан
2 ние (6.89) устойчиво (имеем
()
[]
0, <τδ tH
,
[] []
0,
21
=
=
PEP
), из (6.93) получим известное вы-
ражение для в жденного решения ыну
() ( )
[]
()
∫
∞−
=
t
dftHty
τττ
,
. (6.95)
В случае, когда
()
[]
0, >τ
γ
tH
(уравнение (6.89) неустойчиво),
налогично получаем:
а
Решением уравнения (6.89) может быть выражение типа (6
интервалом интегрирования [15]
4
.92) с конечным
[]
ab,
()
()
[]
()
()
[]
()
yt Ht f d Ht f d
a
t
t
b
=−
∫∫
,,τττ ττ
12
τ
.
108
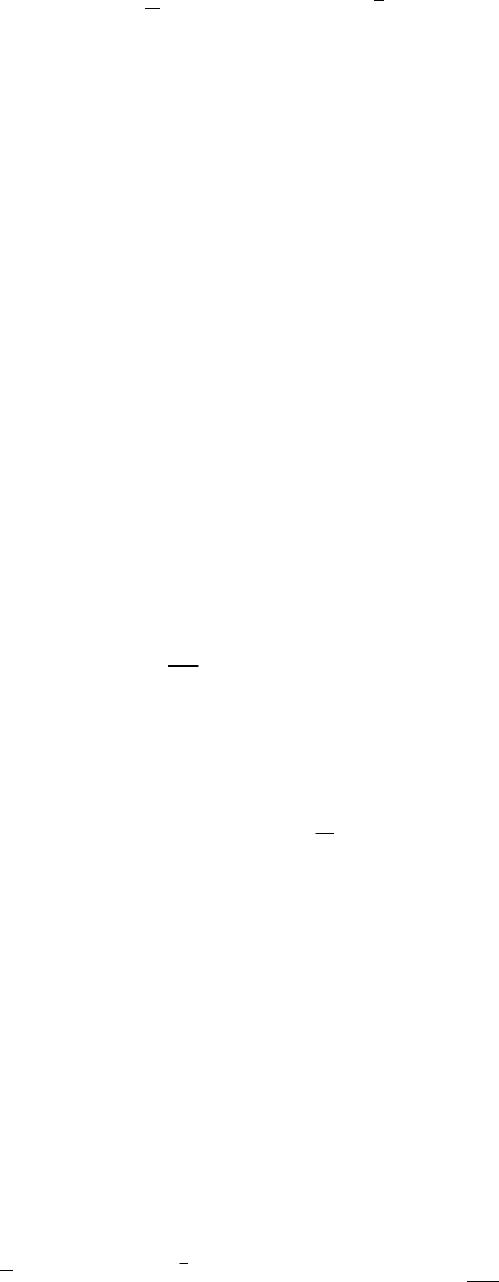
() ( )
[]
()
∫
∞
−=
t
dftHty
τττ
,
. (6.96)
л тся “физически невозможным”, т.к. его
нел еали
ПРИМЕР
Возможность существования ограни
можно показать на таком примере.
Пусть имеем простейший объект, описываемый уравнением с
го порядка
Это решение яв яе
ьзя р зовать экспериментально, поскольку переходный про-
цесс в системе неограниченно возрастает. Однако решение (6.96)
можно подтвердить и из опыта, если объект охватить обратной це-
пью, сообщающей ему устойчивость [44].
Выражение (6.96) позволяет получить аналитически устано-
вивший режим объекта, физическая реализация которого в прин-
ципе возможна после обеспечения устойчивости объекта схемными
путями.
6.2
ченного установившегося решения (6.96)
остояния перво-
const, =+= afay
dt
dy
, (6.97)
который экспоненциально дихотомичен при
0
≠
a
.
Если положить
const
=
=
c
ff
, то
const
=
=
c
находится из уравнения
yy
cc
fy
1
−=
a
которое является уравнением стат о
, (6.98)
ическ й характеристики объекта (6.97) и имеет
смысл при любом
0≠a
. Функция Грина объекта (6.97) при
0<a
имеет вид:
()
[]
(
)
[]
(
)
[
]
(
)
[
]
()
⎩
⎨
⎧
<
==
=
−
−
,,0
,,,
,
1
τ
τττ
τ
τ
t
>textxtH
tG
ta
(6.99)
при
вшееся решение в соответствии с формулами (6.95), (6.96) будет:
0>a
()
[]
()
()
⎩
⎨
<−=−
=
−
.,,
,
ττ
τ
τ
tetH
tG
ta
(6.100)
Установи
⎧
,,0
t>
τ
() ( )
[]
()
()
0,, <−===
∫∫
∞−
−
∞−
a
a
f
d
c
τ
fedftGty
t
c
ta
t
τττ
τ
; (6.101)
109
