Афанасьев А.А. Математические основы теории систем управления
Подождите немного. Документ загружается.


Теорем а 7.2
Если хотя бы одно собственное значение
()
nj
j
,,2,1 K=
λ
матрицы
[]
A
квазилинейного уравнения (7.8)
ельной вещественной частью, то
обладает положи-
т положение равновесия
a
x
=
неустойчиво.
Теорема 7.3
Если среди собственных значений матрицы
[
]
A
квазилинейно-
го уравнения (7.8) имеется нулевое значение
(
)
0
=
λ
j
или два чисто
мнимых значения
(
)
jj
ω±=
λ
, а остальные значения
имеют отрицательные вещественные ст устойчивости
положения равновесия
собственные
об
ча и, то
a
x
=
нельзя судить линейному уравне-
ного слагаемого
по
нию без учета малого нел еин й
(
)
y
.
g
значений матрицы
[
он не представляет ин-
Этот случай расположения собственных
называют критическим. Для практики
указан-
с начений. твенные зна-
должны находиться на достаточно большом асстоянии от
границы устойчивости (большем некоторой величины , называе-
запасом у
7.2. УСТОЙЧИВОСТЬ В “МАЛОМ” НЕАВТОНОМНЫХ
Рассмотрим неавтономную систему
]
A
ых
чения
тереса, так как соответствует граничному расположению
н обственных з В реальных системах собс
р
d
мой стойчивости).
НЕЛИНЕЙНЫХ СИСТЕМ
()
txf
dt
xd
,=
. (7.10)
Будем предполагать, что вектор-функция
(
)
txf ,
дважды не-
прерывно дифференцируема в некоторой области:
Hxt
<
≥ ;0
.
Пусть
()
tx η=
- некоторое решение системы (7.10), удовле-
творяющее условию
130
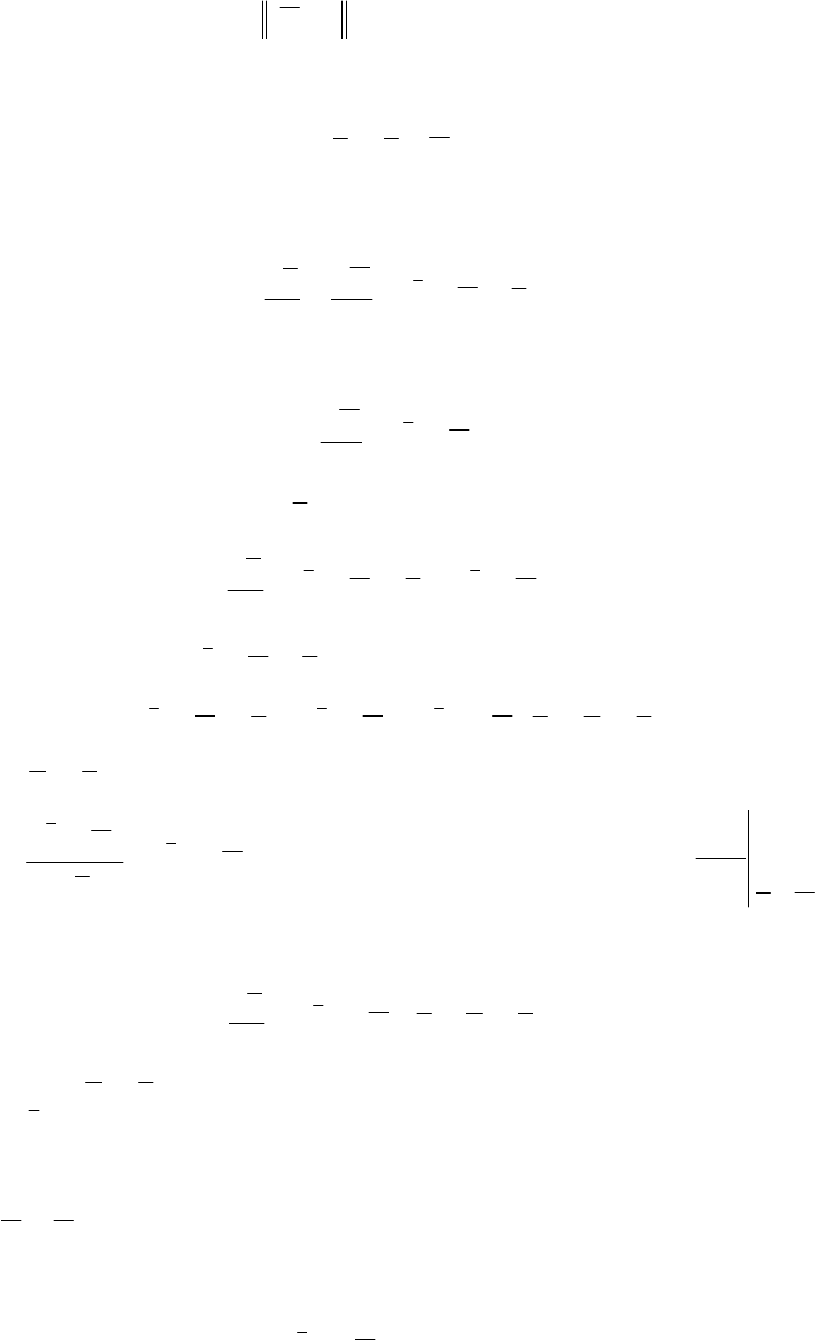
(
)
Ht
<
η
при
0≥
t
.
удем полагать это решение невозмущенн
Положим
Б ым движением системы
(7.10).
η
−
=
x
y
- отклонение решения от возмущенного движения. Тогда из (7.10)
имеем:
(7.11)
()
ytf
dyd
+η=
dtdt
η
+ ,
.
Принимая во внимание, что
()
η=
η
,tf
d
t
d
,
получим для отклонения
y
:
()()
η−+η= ,, tfytf
dt
yd
. (7.12)
вая Расклады
()
ytf +η,
в ряд Тейлора, запишем:
()
(
)
(
)
(
)
ytgytftfytf
x
,,,, +η
′
+η=+η
,
()
−ytg ,
где остаточный член;
()
()
η
′
=
∂
,tf
x
x
- матриц с элементами
η,tf∂
а Якоби
)(tx
x
j
η=
∂
.
Следовательно, уравнение (7.12) можно переписать
f
i
∂
в таком виде
()
[]
()
ytgytf
d
t
y
x
,, +η
′
=
,
d
(7.13)
()
где
0,lim
0
=
→
ytg
y
.
Квазилинейное уравнение (7.13) называют первой вариацией
неавтономной системы (7.10) отн льосите но невозмущенного реше-
ния
()
tη=η
, или уравнением неавтономной системы в вариациях,
или линеаризованным неавтономным уравнением.
Если обозначим
(
)
(
)
(
)
[
]
tAttf
x
=η
′
,
,
131

то
уравнение (7.13) запишется так:
()
][
(
yyt
)
A
d
t
yd
=
. (7.14)
0+
(
)
t
η
=
η
Невозмущенное решение системы (7.10) называется
симптотически устойчивым, если
удет решение для отклонения
а асимптотически устойчивым
б
(
)
ty
.
решен Асимптотическая устойчивость ия
(
)
t
η
=
η
означает,
что если величина
()
(
)
(
)
000
η
−
=
xy
достаточно мала, то
(
)
(
)
0lim
=
t
,
−
η
∞→t
tx
то есть точки фазовой траектории возмущенного решения
()
tx
при
∞→
t
неограниченно сбл ами фазовой траектории ижаются с точк
невозмущенного решения
()
tη
.
Устойчивость траектории называют также орбитальной ус-
тойчивостью.
положим теперь, что правая часть уравнения (7.10) пе-
риодична во времени
Пред
()
(
)
txfTtxf ,, =−
,
где
T
- период.
Невозмущенное решение
(
)
t
η
=
η
также периодично и имеет
ериод
T
п . Тогда уравнение в вариация
ную систему с периодическими коэффициентами.
Если все характеристические уравнения в ва-
риациях для данного период ения
х (7.14) представляет линей-
Теорема 7.4 (Ляпунова)
показатели
ического реш
j
x
(
)
t
η
имеют отрица-
ки усто
тельные вещественные части, то это периодическое решение
асимптотичес йчиво при
∞
→
t
.
132
7.3. СТРУКТУРА РЕШЕНИЙ АВТОНОМНОЙ СИСТЕМЫ
Лемма 7.1
Если автономная система
)(xf
dt
=
(7.15)
допускает невозмущенное решение
xd
(
)
t
η
=
η
, не являющееся тож-
дественной постоянной (точкой равновесия), т.е.
0)( ≠η
•
t
, то
)(ty
•
η=
(7.16)
является решением ее уравнения в вариациях.
Доказательство
Дифференцируя по t тождество
))(()( tft η=η
•
s
,
получим:
)())(()( ttft
d
t
d
x
•
•
ηη
′
=η
s
или, с учетом (7.16), имеем:
yf
dt
yd
x
)(η=
′
s
. (7.17)
Сравнивая (7.17) с (7.13), убеждаемся в справедливости лем-
мы.
Лемма 7.2
Если автономная система (7.15) допускает - периодиче-
ское решение
T
()
tx η=
, то для соответствующего уравнения в ва-
иях
риац
yf
dt
yd
x
)(η
′
=
s
, (7.18)
133
представляющего собой л иодическую систему, по
оди
инейную пер
меньшей мере н из ее мультипликаторов
1
=
ρ
, т.е., по меньшей
мере, один из характеристических показателей системы (7.18) яв-
ляется нулевым.
Доказательство
С огласно лемме 7.1,
T
- периодическим решением уравнения
в отклонениях (в вариациях) будет зависимость
0≠
η
=
dt
d
y
(производная от периодического решения будет также периодиче-
ласно замечанию 3.1 (глава 3) перио-
(7.18) будет иметь, по крайней мере,
один мультипликатор . Тогда соответствующий ему характе-
ен нулю
ской функцией). Поэтому сог
дическая однородная истема с
1=ρ
ристический показатель будет рав
01ln
1
ln
1
=ρ=λ =
T
T
.
7.5
.15) допускает
Теорема
T
Пусть автономная система (7 - периодиче-
ское решение
()
tη
, не являющееся тождественной постоянной
)0( ≠
η
=
dt
d
y
, причем уравнение в ва
ния имеет один простой нулевой характеристический показатель,
а остальные - с отрицательными действительны
риациях (7.18) этого реше-
м частями. То-
да п
для
и
г ериодическое решение
(
)
tη
асимптотически орбитально ус-
тойчиво при
∞→
t
.
Если
()
Δ
<
η
−
)0(0x
,
где дос
Δ>0
таточно малое число, то (см. рис. 7.1)
(
)
(
)
lim 0
=
η
−
∞→
ttx
t
.
Следующая теорема [41] посвящена классификации ений
автономной системы
реш
(7.15).
134
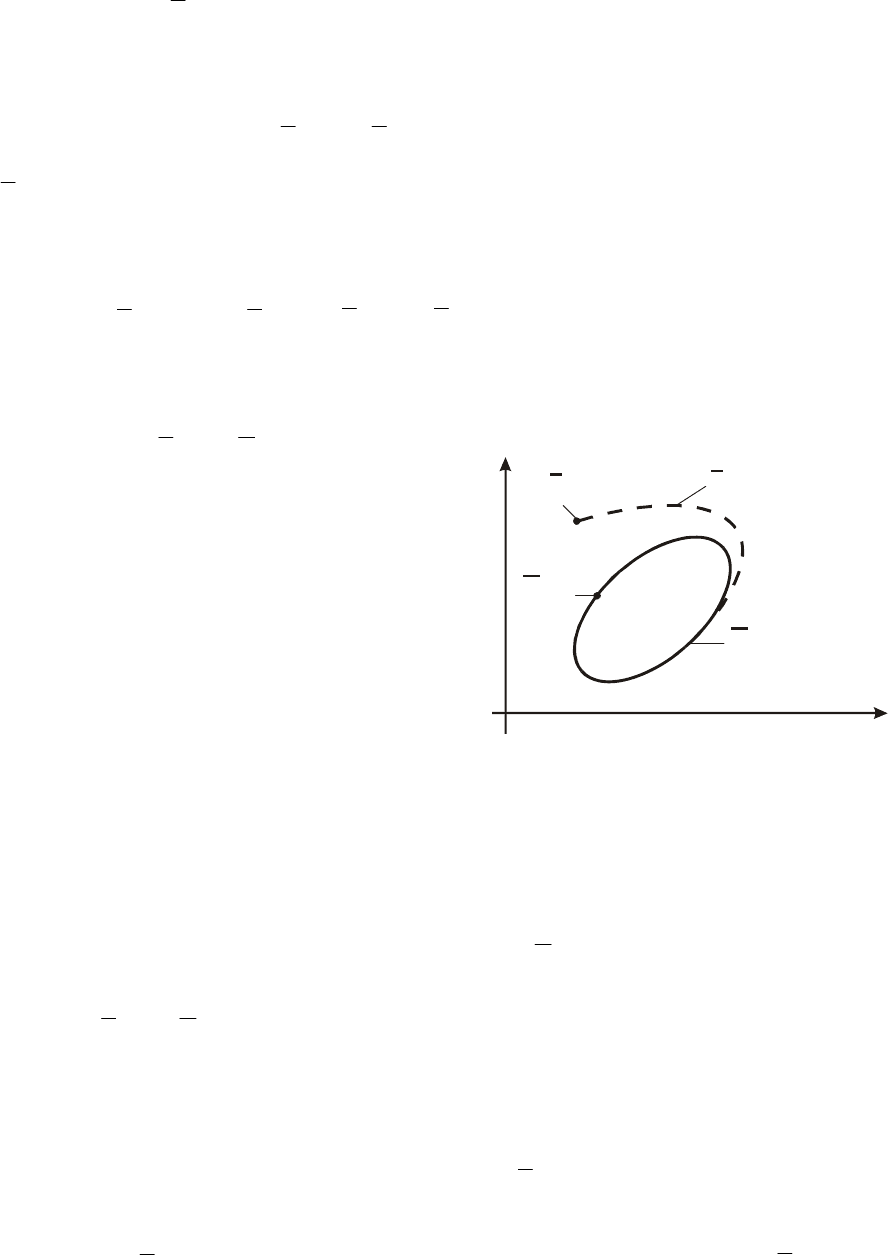
Тео
Решение
рема 7.6
()
tx
автономной системы (7.15) может быть толь-
ко одного из с иледующ х трех типов:
а) непериодическое, для которого
(
)
(
)
2
tx
1
tx
≠
при
21
tt
≠
.
()
tx
- гладкая кривая без
б) периодическое, для кото тся такое постоянное
самопересечений;
рого найде
0>
T
(период), что
()()
txTtx ≡
+
, а
(
)
(
)
2
t
1
xtx
≠
Ttt <<
<
21
0
при .
Имеем замкнутую гладкую кривую (цикл);
в) постоянное, для которого
()
atx ≡
.
без самопересече-
Отметим, что траектория, о
личная от точки покоя, представ
x
n
x
(
t
)
x
(0)
зовая траектория - точка. Фа
Траектории, отвечающие ре-
шениям указанных типов, называ-
ются соответственно незамкнутой
(траектория
η
(0)
η
()
t
ний), замкнутой и точкой покоя.
Замкнутая траектория иначе
называется циклом.
x
1
0
Рис. 7.1. Периодическое решение
асимптотически орбитально
устойчиво
т-
-
ляет собой ориентированную линию, т.е. линию, вдоль которой
указано направление, принятое за положительное.
Отметим также, что точка покоя
a
называется устойчивой
оот (с ветственно асимптотически устойчивой, неустойчивой), если
решение
()
atx
≡
системы (7.15) является устойчивым (асимптоти-
чески устойчивым, неустойчивым) (см. тео ему 7.1). р
Предельное поведение траекторий
Рассмотрим какое-либо решение
(
)
tx
системы (7.15) и соот-
ветствующую траекторию l.
Точка называется предельной точкой решения
(
)
tx
∗
x
(или
траектории l) при
+
∞→
t
, если существует последовательность
135
моментов
+∞→
k
t
, такая, что
(
)
∗
→ xtx
k
. Совокупность всех таких
точек называется предельным множеством для рассматриваемого
решения при
+∞→
t
.
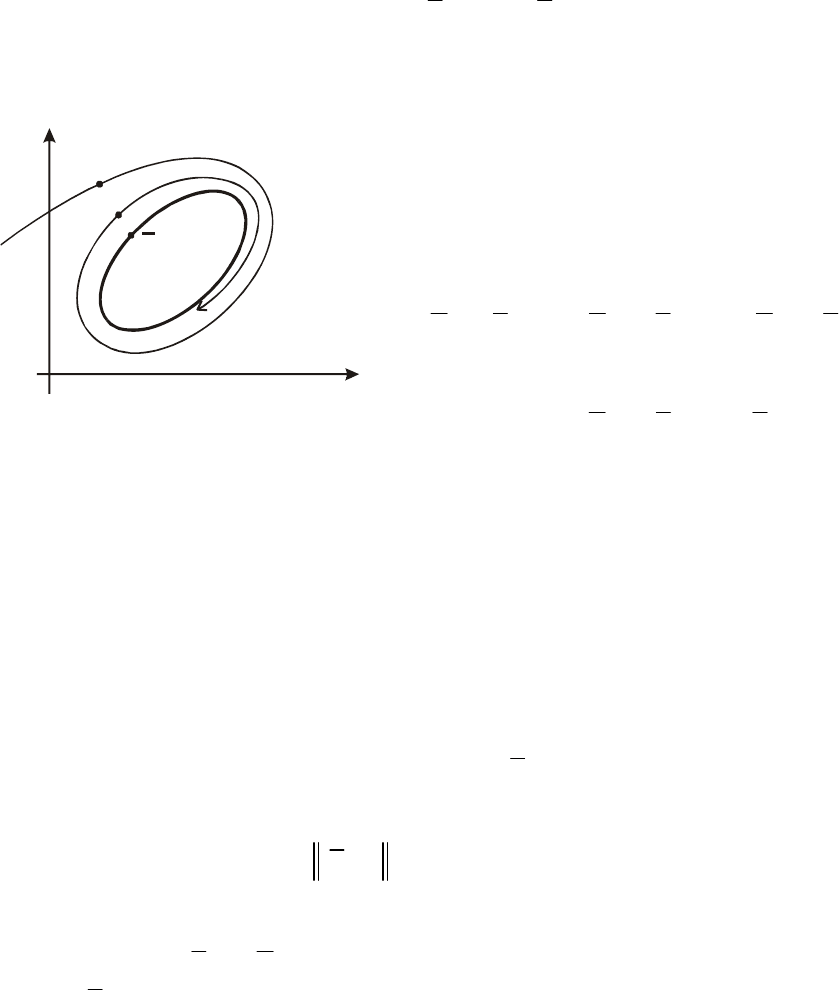
Траектория l спиралевидно при-
к циклу l
*
(рис. 7.2). Нетруд-
видеть, что этот цикл и служит пре-
множеством для l при
ближается
но
дельным
+∞→
t
.
точек Для
(
)
(
) ()
kk
txatx =atxa
=
=
K,
22
,
11
имеем
(
)
∗
= x
.
∞→
= txa
kk
t
k
lim
Замкнутая траектория является
своим предельным множеством присобственным
∞
→
t
.
1.
Предельное замкнуто как точечное множество в n -
ме
Рассмотрим некоторые свойства предельных множеств.
множество
рном пространстве (т.е. содержит все свои предельные точ-
ки).
2.
Для того чтобы предельное множество было пустым, необхо-
димо и достаточно, чтобы линия
(
)
tx
при
+
∞→
t
уходила в бес-
конечность, т.е. чтобы
()
∞
→tx
при
∞
→
t
.
3.
Для того предельное множество состояло из единствен-
ной точки
чтобы
a
x
=
∗
, необходимо и достаточно, чтобы траекто-
рия
()
tx
входила в эту точку при
t →
+
∞
.
аектория (цикл) называется устойчивой, если
траектории ающиеся снаружи или внутри цикла, спирале-
видно приб
Замкнутая тр
, начин
лижаются к циклу (рис. 7.3, а).
Если траектории (внутренние и наружные) удаляются от цик-
ла, то имеем неустойчивый цикл (рис. 7.3, б).
x
1
0
x
2
a
1
a
2
l
x
*
l
*
Рис. 7.2. l - предельное
множество траектории l
*
136

или внутри) траекто-
р дятся, то имеем полуустойчи-
Если на одной стороне цикла (снаружи
ии устойчивые, а на другой - расхо
ый ц
О И ФАЗОВАЯ ПЛОСКОСТЬ
еаризации, описываются линейными
двух (реже - нескольких) существен-
но нелинейных звеньев этой системы составляются нелинейные
уравнения (или используются нелинейные характеристики). В об-
щем случае в векторной запис
уравнения имеют вид:
в икл.
а) б)
в)
Рис. 7.3. Замкн
у
тые траектории (циклы)
у
стойчивого (а), не
у
стойчивого (б)
и по уустойчивого (в) типал
7.4 ФАЗОВОЕ ПРОСТРАНСТВ
При составлении уравнений динамики нелинейной системы
се з нв венья, поддающиеся ли
уравнениями. Для одного или
и нелинейные дифференциальные
() ())
tgg
в
,
, (7.19)
(
txf
dt
xd
з
,,=
где
t
[]
T
n
xxxx
K21
=
- координат
ы состояния системы;
() ()
tgtg
вз
,
- соответствен возмущающие воз-
действия.
При рассмотрении переход
нат
но задающие и
ных процессов, вызванных началь-
твия ными отклонениями коорди (внешние воздейс
()
tg
и
(
)
tg
з в
с постоянными (т.е. для
тационарных систем) уравнения (7.19) примут ф
отсутствуют) и для систем параметрами
с орму
137
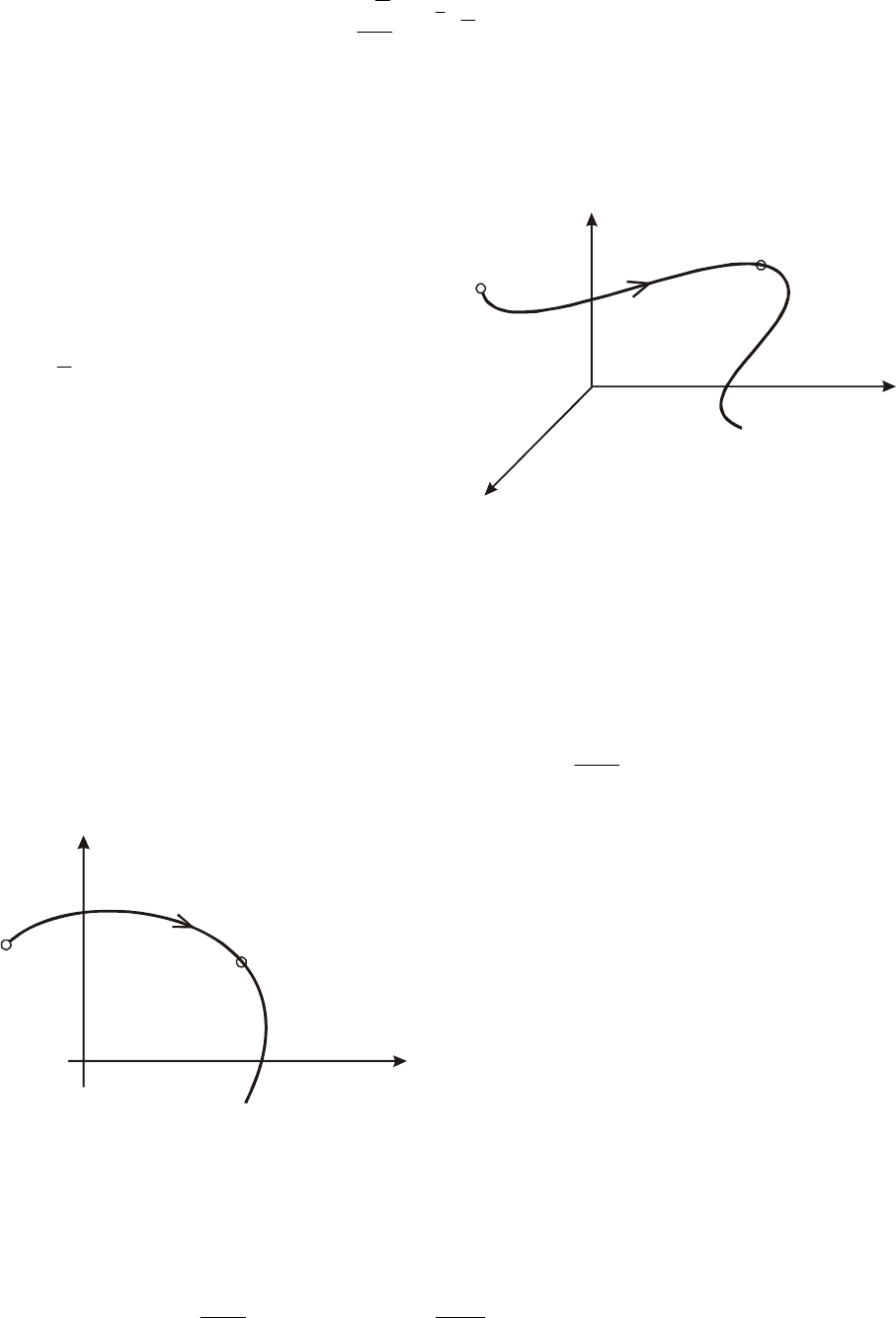
()
xf
dt
xd
=
. (7.20)
стем широко используется
м образуют координаты со-
Для исследования нелинейных си
етод фазового пространства, которое
системы в момент изобра-
жается точкой координа-
стояния системы
n
xxx ,,,
21
K
.
В этом пространстве
(рис.7.4) начальное состояние
0
tt =
()
с
0
tM
тами
()
0
tx
, а процесс во времени,
.е. решение уравнения (7.20)
ая времени t, называ-
ется изображающей точкой.
Значение правой части
т
() () ()
txtxtx
n
,,,
21
K
,
изобразится в виде некоторой
кривой, которая называется фа-
зовой траекторией системы.
Текущая точка М на ней, соответствующ
()
ni
dt
f
i
i
,,2,1 K==
dx
формуле (7.20) является анало-
скорости
i
v
изображающей
в механической системе.
Картина, которую образуют
фазовых траекторий,
название: фазовый портрет
(7.20).
Для двумерных систем
в
гом
точки
несколько
носит
системы
(
)
2
=
n
лагается
фазовая траектория распо-
на плоскости (рис.7.5).
Уравнения (7.20)
2
принимают вид
для
=n
() ()
212
2
211
1
,,, xxf
dt
dx
xxf
dt
dx
==
. (7.21)
Mt
()
0
Mt
()
3
n
0
равнения
x ,...,x
x
2
x
1
Рис. 7.4. Фазовая траектория у
состояния
x
2
Mt
()
0
0
Рис. 7.5. Фазовая траектория
двумерного уравнения состояния (7.20)
Mt
()
x
1
138
ся
из (7.21) пу
Дифференциальное уравнение фазовой траектории получает
тем исключения времени t:
(
)
()
211
212
1
2
, xxfdx
=
. (7.22)
Точки равновесного состояния системы определяются нуле-
выми значениями скорости
, xxfdx
0,0
21
==
dt
dx
dt
dx
.
Поэтому в этих точках имеем
()
,0,
211
=
xxf
(
)
,
212
=
xxf 0
, (7.23)
что создает неопределенность правой части уравнения (7.22). Сле
тельно, решения уравнен
(7.21) ками на фазовой плоскости.
Наряду с обычным изображением решения системы (7.20)
применяют
-
дова ий (7.23) - точки равновесия системы
- являются особыми точ
()
t
k
x
также изображение в виде
()
k
k
xf
dt
dx
=
.
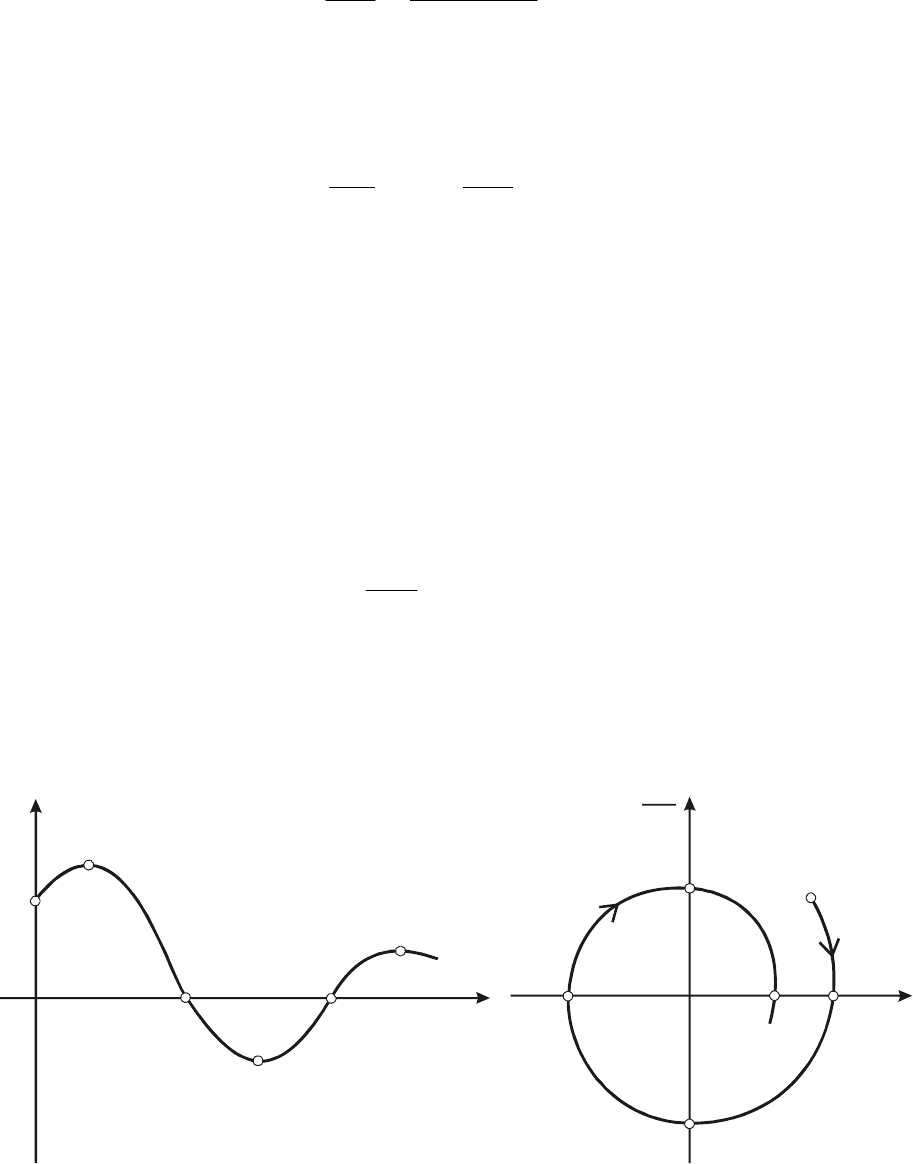
В колебательный процесс этом случае, например, затухающий
.(рис 7.6, а) изобразится в виде сходящейся спиралевидной кривой
(рис.7.6, б).
0
x
0
1
x
1
t
C
D
A
F
F
A
B
C
D
E
E
dt
B
dx
1
Рис. 7.6. Способы изображения координатных составляющих решения уравнения
состояния (7.20)
139
