Афанасьев А.А. Математические основы теории систем управления
Подождите немного. Документ загружается.


()
(
)
(
)
τ
τ
= ytRty ,,
, (8.17)
где
() ()
τ=
=τ
t
tyy
начальное ачение переменных.
щем функцию Ляпунова
- зн
И
()
ytV ,
, удовлетворяющую в силу систе-
мы (8 уравн
.16) дифференциальному ению (8.13)
() ()
(
FV
t
ytV
d
t
ytdV
grad
,,
⋅+
∂
)
()
ytWyt ,),( −=
∂
=
е
, (8.18)
гд
()
ytW ,
- определенно положительная функция, непрерывная
и дифференцируемая по t и
y
в облас
Функцию
ти .
G
()
ytW ,
будем считать заданной, например, в виде
положительно определенной квадратной формы (8.7):
() ()
[]
()
ji
n
j
ji
T
yytbytByytW
∑
=
==
1
,
.
овий
i
,
Предполагая выполнение усл
()()
(
)
0,lim,0,,lim
0,0
=
=
τ ytVytR
,
из формулы (8.18) после ряда преобразований можем получить вы-
ражение для функции Ляпунова
τ
≥→∞→ tyt
[
]
11
2
:
() ()()
)
dstyts
∞
,,
. (8.19)
(
RsWytV
∫
= ,,
t
2
Действительно, интегрируя (8.18) с учетом (8.17), будем иметь:
∫∫
∞∞
−=
tt
dstytsRsWds
ds
tytsRsdV
)))(,,(,(
)))(,,(,(
Поскольку
0)))(,,(,(
=
∞=
s
tytsRsV ,
то
()()
()
dstytsRsWytVtytsRsV
t
t
∫
∞
∞
−=−= ),()))(,,(,(
Этот результат совпадает с формулой (8.19).
,,, .
160
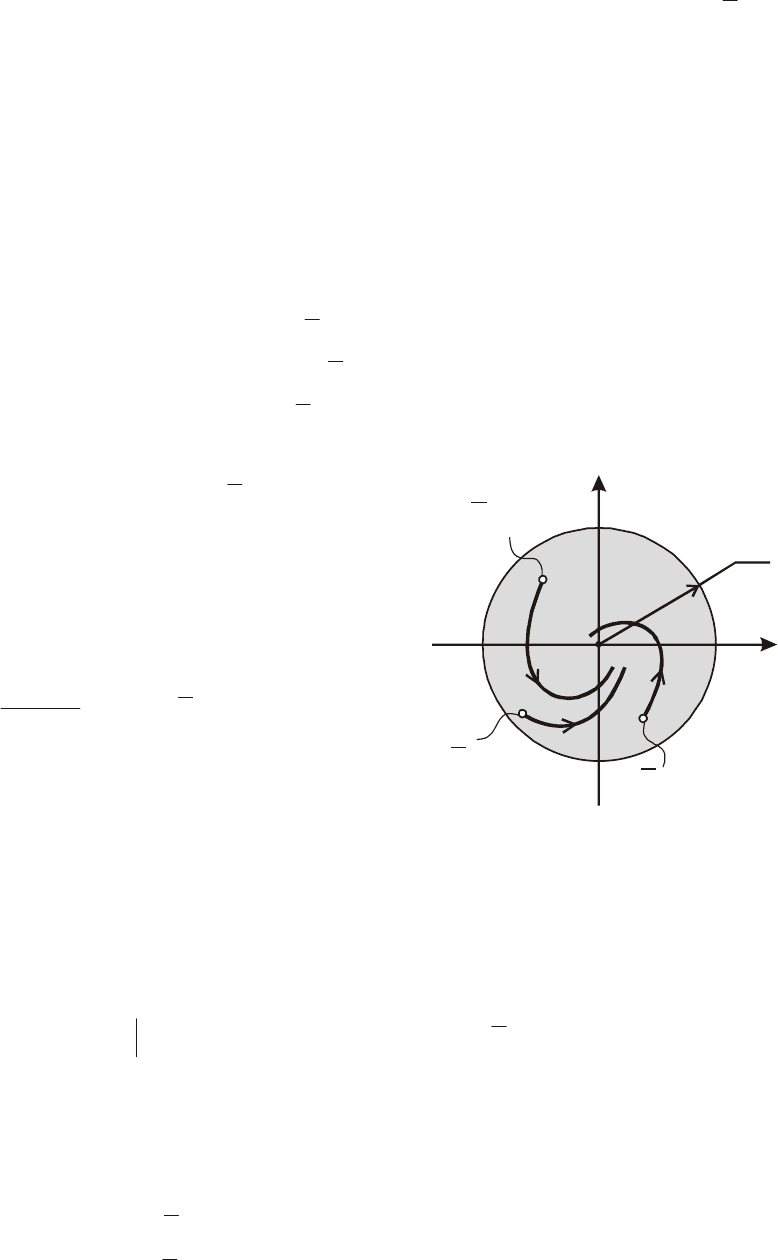
Используем эту формулу для построения вычислительного ал-
горитма, обратив внимание, что аргументы левой части (t и
y
) яв-
ляются начальными значениями уравнения состояния (8.16).
.
Задаемся рядом значений 1
(
)
Nktt
k
,,2,1 K
=
=
,
охватывающих интервал изменения параметров в нестационар-
ной системе или интервал изменения функций задания и возму-
м. формулу (7.19)).
Для каждого выберем
щения (с
k
t
k
y
из области асимпто-
тически устойчивого решения
притяжения
0
=
y
.
я
(
)
kk
ty
Рассматривая значени как начальные для системы
(8.16), найдем
k
решений
соответствующих
численных
(
)
t
(рис.
8.7).
йдем ч
y
k
y
1
y
n
2.
На исленное решение систе-
мы дифференциальных уравнений
()
()()
tytW
dt
tdz
k
k
,=
(8.20)
с начальным условием
(
)
0
=
kk
(достаточно большом)
tz
на
интервале
[
]
Ttt
kk
+,
.
ри интегрировании уравнения
(8.20) имеем:
П
∫
+
+
=+=
kk
Tt
k
k
sTtzsz ,)()(
Tt
k
t
k
k
dssyW ))((
.
3.
С помощью интерполяционных формул восстанавливается функ-
ция Ляпунова
t
k
Это выражение аналогично (8.19).
()
, для которой известны прибли
чения в точках
ytV ,
t
,
женные зна-
k k
y
(рис.8.7)
0
y
11
()
t
δ
y
22
()
t
y
()
t
kk
Р
ис.8.7. К построению функций
Ляпунова
161

()( ) ()()
()
dstytsRsWTtzytV
Tt
kkkkkkk
k
,,,,, ≅+=
∫
+
Nk
t
k
,,2,1 K=
(8.21)
ав-Вычислительный алгоритм существенно упрощается для
тономной системы дифференциальных уравнений
() ()
00, == FyF
yd
. (8.22)
dt
1. Задаемся определенно положительной функцией
()
yW
, напри-
мы
мер, в виде определенно положительной квадратичной фор
()
[]
ji
n
i
ij
T
yycyCyyW
∑
==
(8.23)
j
=1,
и из уравнения
()
()
yWyFVgrad
dt
ydV
−=⋅= )(
)(
и условий
(
)
0lim lim;0
0
=
= yVy
→∞→ yt
находим
)( y
V
по формуле
() ()
()
dtytRWyV
∫
∞
=
0
,
, (8.24)
где
)0(yy =
- начальное значение уравнения состояния (8.16).
2. Для отыскания значений функции Ляпунова
(
)
yV
при
(
)
Nkyy
k
K,2,1
=
=
решаем численным способом систему дифференциальных уравне-
ний:
162
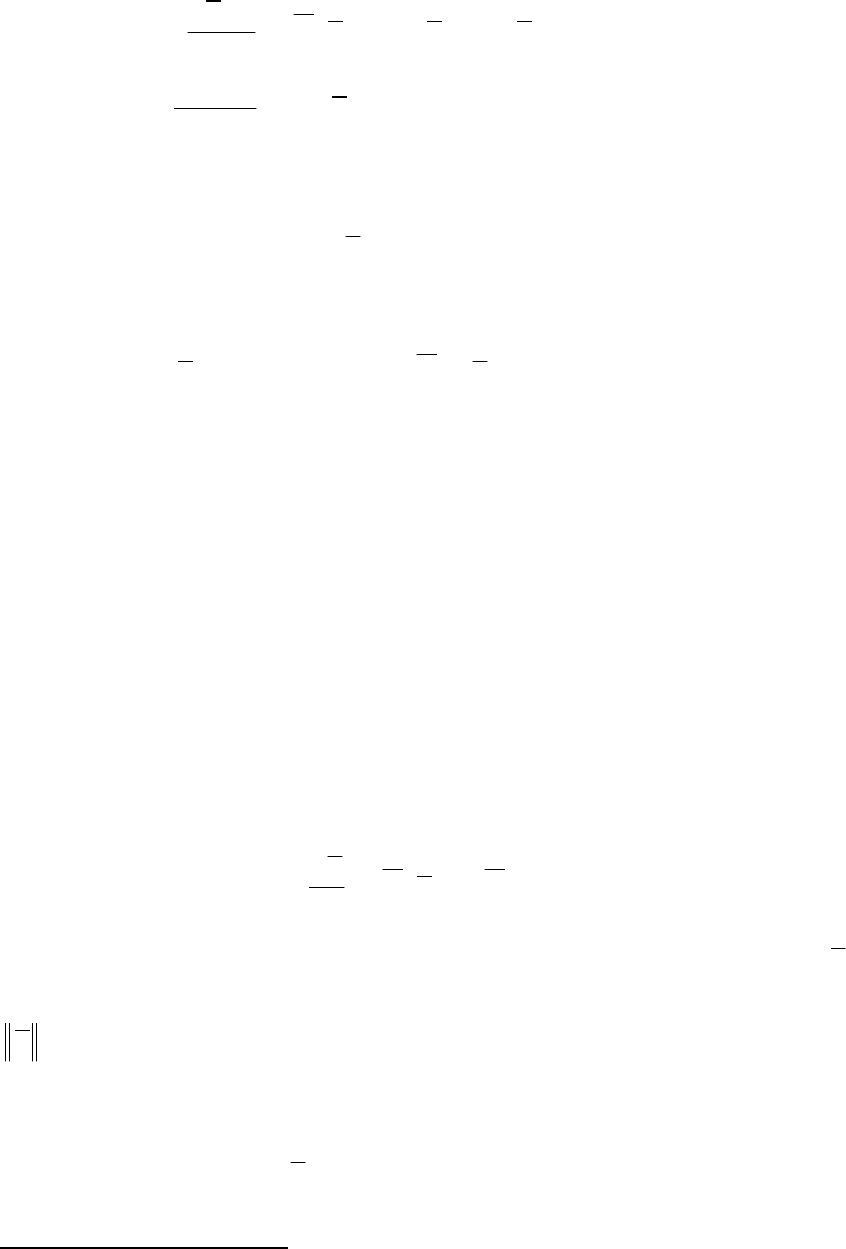
()
()
()
Nk
ztyW
dt
tdz
yytyF
dt
tyd
k
k
K,1
)(
;)0(,)(
)(
=
⎪
⎪
⎬
⎫
==
(8.25)
kk
;0)0(,)(
⎭
==
на достаточно длительном интервале
[
]
T,0
.
(
)
yV
3. Функция Ляпунова восстанавлива
ляционных формул из уравнений
ется с помощью интерпо-
() () (
(
tRWTzyV
T
kk
,≅=
∫
)
)
()
Nkdty
k
K,1,
0
=
. (8.26)
Таким образом, функции Ляпунова, найденные рассмотренными
исленными алгоритмами для уравнений состояния (8.
соответствуют областям асимптотической устойчивости (областям
притяжения) этих уравнений, конфигурация которых выявляется из
УНОВА ДЛЯ НЕЛИНЕЙНЫХ
ДИФФЕРЕНЦИАЛЬНЫХ СИСТЕМ МЕТОДОМ ГАЛЕРКИНА
При построении функций Ляпунова для автономной нелиней-
ч 16) и (8.22),
этих же численных расчетов.
8.4.2. ПОСТРОЕНИЕ ФУНКЦИЙ ЛЯП
ной системы дифференциальных уравнений в отклонениях:
() (
0;= FyF
yd
)
0=
dt
, (8.27)
имеющей асимптотически устойчивое нулевое решение
0
=
y
часть
и
достаточное число раз дифференцируемую правую при
Hy <
, наиболее эффективным оказался следующий способ ис-
ользования метода Галеркина [11].
ыбираем набор координатных функций
п
3
1.
В
()
(
)
(
)
Nk
k
K,2,100y ,
=
=
ψ
ψ
,
Координатными функциям в методе Галеркина называют набор линейно незави-
мых
3
и
си непрерывных функций (вместе с первой производной) в заданной области с
фиксированными граничными условиями
(
)
ψ
k
00
=
[21].
163

которые имеют непрерывны по всем аргу-е частные производные
ментам
()
n
yyy K,,
21
при
Hy
<
. Это могут быть, например,
функции вида:
()
()
()
21
.
,
2
2
2
1
211
n
yyyy
yyy
+++=ψ
,
2
n
y
+
+
+
2
N
n
NN
N
yyyy +++=ψ
=ψ
K
K
2.
Задаем определенно положительную функцию
K
K
(
)
yW
в виде ли-
нейной комбинации координатных функций:
() ()
∑
=
ψβ=
N
k
kk
yyW
1
. (8.28)
3.
Определенно положительную функцию Ляпунова будем искать
также в виде линейной комбинации координатных функций
() ()
yyV
N
k =
1
kk
∑
ψγ=
. (8.29)
Для производной от координатной функции по времени, в си-
системы, находим разложение лу
()
()
()
()
.
1
2
21
1
∑
=
ψα=⋅ψ=
=
∂
∂
ψ
++
∂
∂
ψ
+
∂
∂
ψ
=
ψ
s
sksk
n
n
kkkk
yyFgrad
dt
dy
ydt
dy
ydt
dy
ydt
yd
r
K
(8.30)
Коэффициенты этого разложения
N
ks
α
известны.
4.
Уравнение для функции Ляпунова
()
()
yW
dtdt
s
k s
kks
k
k
===
111
d
ydV
N NN
k
−=ψγα=
ψ
γ=
∑∑∑
с помощью предыдущих разложений несложно привести к системе
линейных алгебраических уравнений:
164
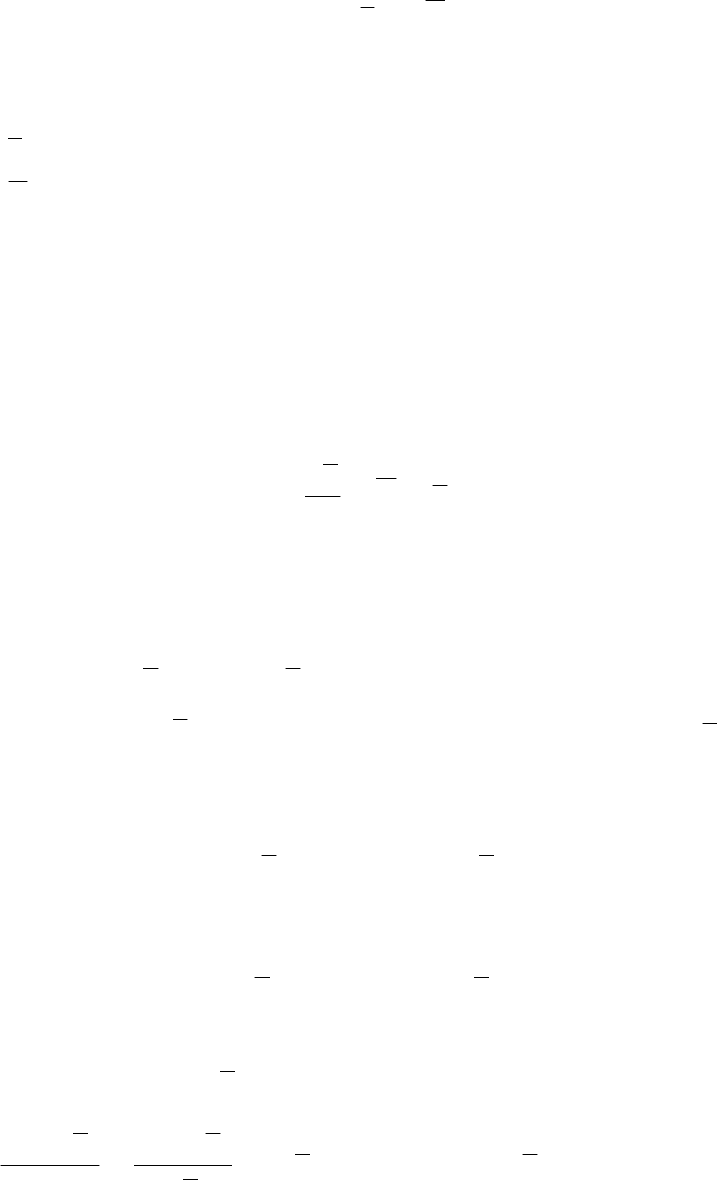
()
Ns
s
N
kks
K,2,1=β−=γα
∑
,
k
1=
которую запишем в векторно-матричном виде
[
]
β−=γα
, (8.31)
- элемент квад
где
ратной матрицы
[]
α
;
()
Nsk
ks
K,2,1, =α
[]
N
T
γγγ=γ K
21
- неизвестный вектор;
[]
N
T
βββ=β K
21
.
В результате решения последнего уравнения становится из-
вестной, в соответствии с формулой (8.29), ункция Ляпунова.
для нахождения функции
Ляпунова нелинейной нестационарной системы
ф
Замечание
Рассмотренный метод применим
()
ytF
dt
yd
,=
. (8.32)
ор координатных функций
Изложим идею метода.
1.
Выбирается наб
(
)
(
)
(
)
(
)
kyy
kN
,,2,1,00,,,
1
KK N
ψ
=
=
ψψ
2.
Функция
.
()
ytW ,
задается, а функция Ляпунова
()
ytV ,
ищется в
виде линейной комбинации координатных функций
() ()()
yytW
k
k
β=
∑
=1
,
, (8.33)
N
t
k
ψ
() () ()
ytytV
k
N
k
k
ψγ=
∑
=1
,
. (8.34)
3.
Для функций
()
y
k
ψ
находятся приближенно разложения
() ()
() ()() ( )
NkytytF
y
y
dt
yd
s
N
ks
kk
,,2,1, K=ψα=
∂
∂ψ
=
ψ
∑
. (8.
s
1=
35)
165

4. Уравнение для функции Ляпунова
()
()
() () () () ()
ytWytty
dt
td
dt
ytdV
s
N
s
ks
N
k
k
N
k
k
k
,
,
111
−=ψαγ+ψ
γ
=
∑∑∑
===
при
водится к системе линейных дифференциальных уравнений
()
() () () ( )
Nsttt
td
sk
N
ks
s
,,2,1 K=β−=γα+
γ
∑
,
dt
(8.36)
численно в сторону уменьшения значения t.
8.4.3. ПОСТРОЕНИЕ ФУНКЦИЙ ЛЯПУН
НЕСТАЦИОНАРНЫХ ЛИНЕЙНЫХ ДИФФЕРЕРЕНЦИАЛЬНЫХ
с огра-
иченными коэффициентами
s
1=
которая интегрируется
ОВА ДЛЯ
УРАВНЕНИЙ
Для системы линейных дифференциальных уравнений
н
()
(
[
)
]
()
ty
tyd
(8.3
tA
dt
=
7)
равномерно зас экспоненциально устойчивым нулевым решением -
дается определенно положительная, ограниченная по
t
фун в
виде квадратичной формы
кция
()
(
)
[
]
ytByytW
T
=,
и ищется функция Ляпунова (также в виде определенно положи-
тельной квадратичной формы)
()
(
)
[
]
ytCyytV
T
=,
из уравнения
()
()
ytW
d
t
ytdV ,
,−=
.
уравнение в виде уравнения для
искомой матрицы
Это можно записать матричного
()
[]
tC
()
[]
()
[]
()
[]
()
[]
()
[]
tBtAtCtA
dt
tCd
T
−=++
. (8.38)
()
[]
tC
166
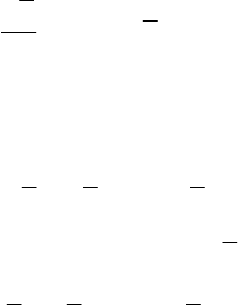
Можно показать [11], что это матричное уравнение имеет
единственное ограниченное при всех
t
решение, которое будет
асимптотически устойчивым при
−
∞→
t
.
Для отыскания матрицы
(
)
[
]
tC
значение
на отрезке можно вы-
брать достаточно большое
[]
βα,
T
и интегрировать матричное
орону с начальным значением уравнение (8.38) в отрицательную ст
(
)
[
]
0
=
+
β
TC
.
Представление матрицы
(
)
[
]
tC
в аналитической форме -
ствляется
ания матрицы
можно использовать алгоритм численного метода Эйлера
осуще
с помощью интерполяционных формул.
При высоких требованиях к точности отыск
()
[]
tC
[] []
(
)
[
]
[
]
[
]
(
)()
[]
{
}
[]
()
[]
.0,
;
0
1
<+=
+−=
+
hnhtCC
tBACCtAhCC
n
nn
nn
T
n
nn
+t
8.4.4. ПОСТРОЕНИЕ ФУНКЦИИ ЛЯПУНОВА ДЛЯ СИСТЕМЫ
-
нений в отклонениях
ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С
ПЕРИОДИЧЕСКИМИ КОЭФФИЦИЕНТАМИ
Рассматривается система линейных дифференциальных урав
()
[]
(
[
tAytA
d
)
]
()
[]
tA
t
yd
+= ;
=π2
(8.39)
асимптотически устойчивым нулевым решени
Задается определенно положительная функция
с ем.
()
(
)
[
]
(
)
[
]
()
[
]
tBytByytW
T
=π+= 2,,
(8.40)
tB
и ищется функция Ляпунова
(
)
ytV ,
в виде вадратичной формы к
()
(
)
[
]
(
)
[
]
()
[
]
tCtCytCyytV
T
=π+= 2,,
. (8.41)
Для вычисления коэффициентов разложения матрицы
(
)
[
]
tC
в
яд Фурье используется следующий вычислитель
адается натуральное число
р ный алгоритм.
N
1. З и находится шаг интегрирования
функции
()
[]
tC
167
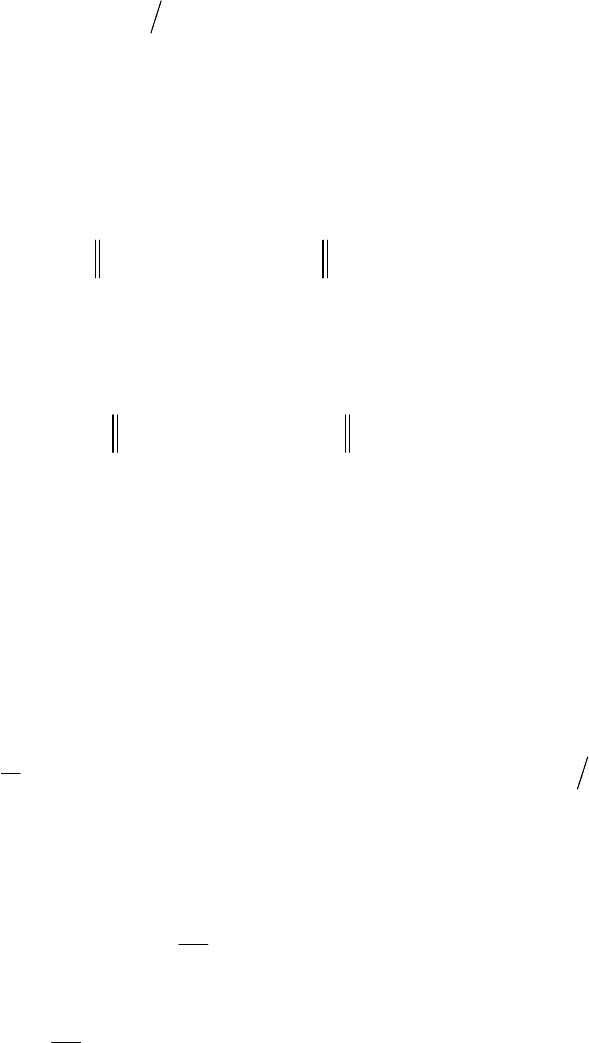
(
)
K,40,20,102
=
π−
=
NNh
.
2.
Вычисление Интегрируется матричное уравнение (8.38)
по извольным начальным значением
.
Вычисляется значение
()
[]
0C
.
методу Рунге-Кутта с про
()
]
0
[
C
(
)
[]
π
−
2C
. Если
()
[]
(
)
[
]
002 >
ε
≥
−
π− CC
- достаточно малое наперед заданное число),
берется за начальное
(
ε
C
то значение
()
[]
π− 2
(
)
[
]
0C
и интегрирование повторя-
ется до выполнения неравенства
()
[]
(
)
[
]
ε
<
−
π
− 02 CC
.
3.
При найденном начальном значении
(
)
[
]
0C
с помощью числен-
ного интегрирования матричного уравнения (8.38) находятся
значения матриц
[]
()
[]
(
)
1,,1,0
−
=
= NnnhCC
n
K
.
4.
Ищется разложение в ряд Фурье
()
[][] [] []
()
()
4sincos
2
1
1
0
NLktBktAAtC
L
k
kk
≤++=
∑
=
по формулам численного разложения в ряд Фурье
[] []
∑
−
=
=
1
0
cos
2
N
n
nk
nkhC
N
A
;
[] []
()
1,,1,0sin
2
1
0
−==
∑
−
=
NknkhC
N
B
N
n
nk
K
.
8.4.5. СВЕДЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ С ПЕРИОДИЧЕСКИМИ КОЭФФИЦИЕНТАМИ К
БЕС
иальных уравнений
с периодическими коэффициентами
КОНЕЧНОЙ СИСТЕМЕ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
Рассмотрим систему линейных дифференц
168
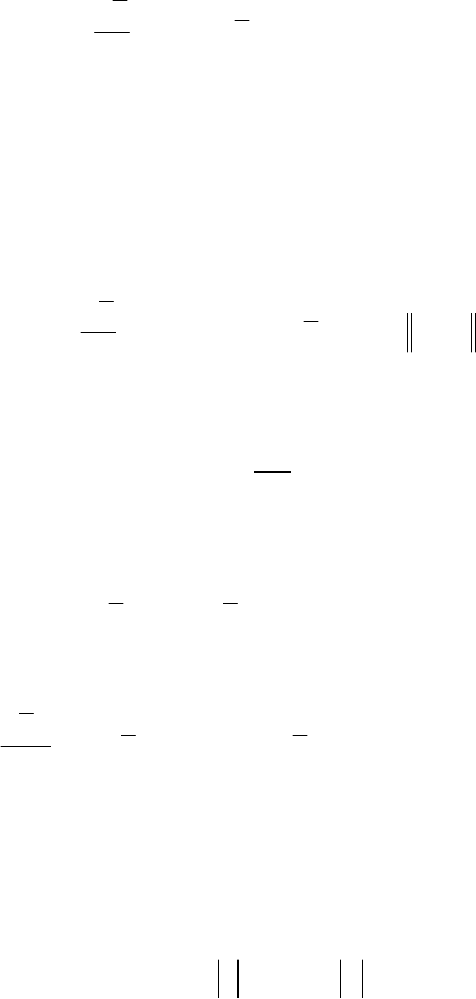
()
[]
()
[]
()
[]
tA
yd
=
. (8.42)
После разложения матрицы
tAytA
dt
π+= 2;
(
)
[
]
tA
в комплексный ряд Фурье
()
[] []
∑
∞
=
jkt
eAtA
−∞=r
k
пол
учим
[] []
∞<=
∑∑
∞
−∞=
∞
−∞= k
k
r
jkt
k
AyeA
dt
yd
;
, (8.43)
где
[]
()
[]
dtetAA
jkt
k
−
π
2
1
∫
π
=
0
2
.
Введем новые переменные
(
)
K,2,1,0, ±±== kyey
jkt
k
. (8.44)
учетом (8.44) система (8.43) примет вид
С
[]
()
K,2,1,0, ±±=+=
∑
∞
−∞=
+
dt
k
sk
k
s
syAyjs
yd
s
. (8.45)
Это будет бесконечная система линейных дифференциальных урав-
нений с постоянными комплексными коэффициентами. Для при-
ближенного исследования бесконечная система уравнений (8.45)
усекается при
NkNs
≤
≤
,
.
строение матрицы Ляпунова для стационарных ли По нейных
8.4.6. СВЕДЕНИЕ НЕЛИНЕ
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ К БЕСКОНЕЧНОЙ
и анализе автономных нелинейных уравнений вида (8.27)
можно воспользоваться следующим приемом. Обозначим нелиней-
уравнений будет рассмотрено ниже.
ЙНОЙ СИСТЕМЫ
СИСТЕМЕ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С
ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
Пр
169
