Афанасьев А.А. Математические основы теории систем управления
Подождите немного. Документ загружается.

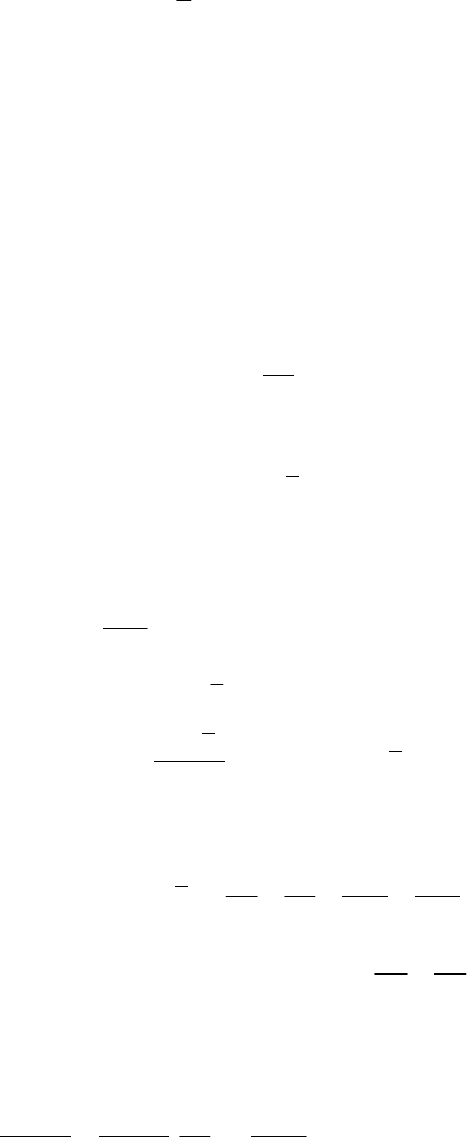
н асти системы (8.27),
через их в силу указан-
ые слагаемые, присутствующие в правой ч
новые переменные и продифференцируем
ез проекции
ной системы. Полученные новые нелинейные слагаемые в правых
частях уравнений, которые не выражаются линейно чер
n
y,,
21
K
вектора
yy ,
y
и введенные переменные, опять обозначаем
через новые переменные и т. д. Изложенный процесс приводит к
есконечной системе линейных диффер
Усечение бесконечной системы уравнений во многих случаях
позволяет найти приближенное решение системы (8.27). Функция
Ляпунова строится уже линейной системы
б енциальных уравнений.
для .
ПРИМЕР 8.1
Ищем функцию Ляпунова для уравнения
2
yy
d
t
dy
+−=
. (8.46)
Выбираем определенно положительную функцию
()
42
yyyW +=
. (8.47)
Сводим нелинейное дифференциальное уравнение к бесконечной системе
линейных уравнений
() ()
K,2,1, ==−−= kyyyyk
1+
d
t
dy
k
k
.
kkk
Функция Ляпунова
()
yV
, найденная из уравнения
()
[]
K
2142
, yyyyy
d
t
ydV
T
=−−=
,
имеет вид линейной комбинации относительно
K,,
21
yy
.
()
()
32
21ln2
5432
32
yy
yy −−−−−=
(8.48)
дя производную от
2
2
5
4
3
2
y
y
y
y
yV =++++= K
В справедливости этого выражения можно убедиться, най
выражения (8.48) по времени в силу уравнения (8.46):
() ()
()
4222
2
1
2
yyyyyy
ydt
dy
y
yV
dt
ydV
−−=+−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−−−
−
=
∂
∂
=
.
170

8
Й
Д
.4.7. ПОСТРОЕНИЕ ФУНКЦИИ ЛЯПУНОВА ДЛЯ СИСТЕМЫ
ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИ
ля системы из
n
линейных дифференциальных уравнений
[]
yA
dt
yd
=
(8.49)
с асимптотически устойчивым
0=y
задается нулевым решением
(
)
yW
определенно положительная функция в виде квадратичной
формы
()
[
]
[
]
[
]
BByByyW
T
T
== ;
(8.50)
(симметричная матрица всегда может быть приведена к диагональ-
9], что выражение (8.24) приводит к фор-
мулам
ному виду с помощью специального преобразования).
Можно показать [1
(
)
[
]
yCyyV
T
=
, (8.51)
0
[]
[]
[]
[]
dteBeC
AtA
T
∫
∞
=
t
4
. (8.52)
Алгоритмы численного нахождения пределенного интеграла
(8 в [11]. Например, можно использовать такой:
о
.52) приводится
[] []
[
]
[
]
[
]
[
][
n
n
n
n
n
nn
CCQCQCC
∞→
∗
+
=+= lim,
1
]
,
гд
- достаточно малое положительное число.
е
∗
h
Q
[] []
[]
[] [] [] []
[]
[]
[]
;;;
0
1
2
11
∫
=====
+
sAsA
nn
hA
dseBeJCQQeQ
0>h
4
Предполагается, что ма
[
]
Aтрица - действительная. При наличии комплексной
матрицы в формулах (8.50)- (8.52) вместо
[]
A y
T
и
[
]
A
T
и
[
]
A
∗
нужно взять y
∗
.
171
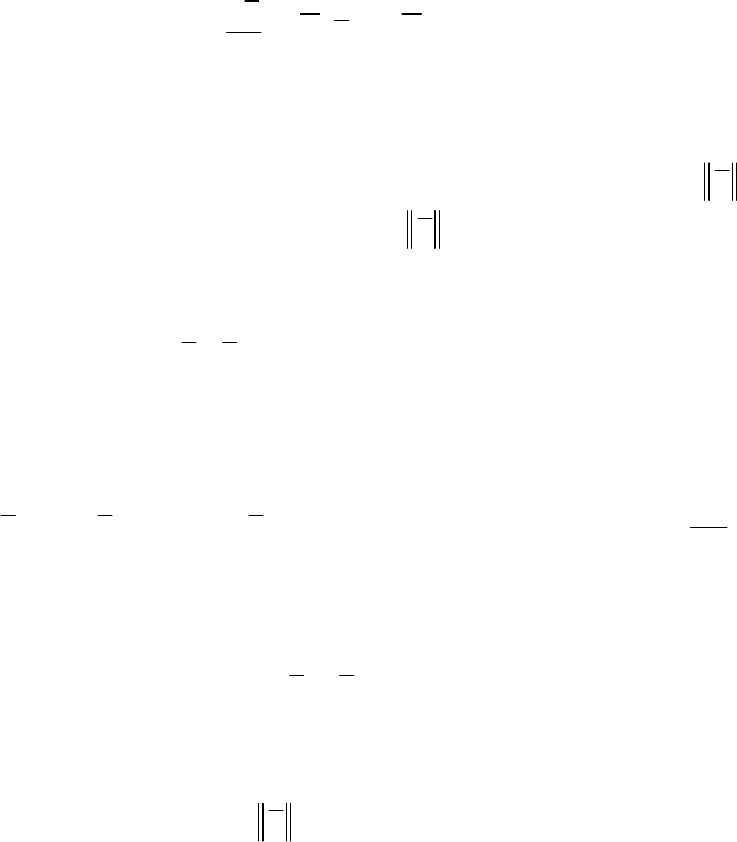
8.5. ПОСТРОЕНИЕ ОБЛАСТИ ПРИТЯЖЕНИЯ
АСИМПТОТИЧЕСКИ УСТОЙЧИВОГО РЕШЕНИЯ
8.5.1. ЧИСЛЕННОЕ ПОСТРОЕНИЕ ОБЛАСТИ ПРИТЯЖЕНИЯ
Рассмотрим систему нелинейных дифференциальных уравне-
ний в отклонениях
() ()
00; == FyF
yd
(8.53)
dt
с асимптотически устойчивым нулевым решением.
Предполагаем, что правая часть системы непрерыв
производными
на вместе с
ρ≤y
частными по всем переменным в области .
Ищем пересечение области
ρ
≤
y
с областью притяжения
нулевого решения. Для этого строим сечения плоскостями, прохо-
мым неколли-дящими через точку
0=y
параллельно двум задавае
неарным векторам
21
, xx
.
Опишем вычислительный алгоритм.
1.
Образуем вектор начальных значений
()
k
N
Nkxxry
kkk
π2
=ϕ=ϕ+ϕ= ;,,2,1,sincos
210
K
.
.
Интегрируем систему уравнений (8.53) по метод
2 у Рунге- Кутта с
начальным условием
0;
0
=
= tyy
.
Зададим промежуток интегрирования
[
]
T,0
и д
окрестность
остаточно малую
(
)
ρ
<
ε
>
ε
≤ 0y
.
При каждом значении
k
ϕ
находим значение
(
)
ρ
≤
≤
=
kk
rrr 0
,
такое, что при
(
)
0>
δ
δ
+
= rr
k
172
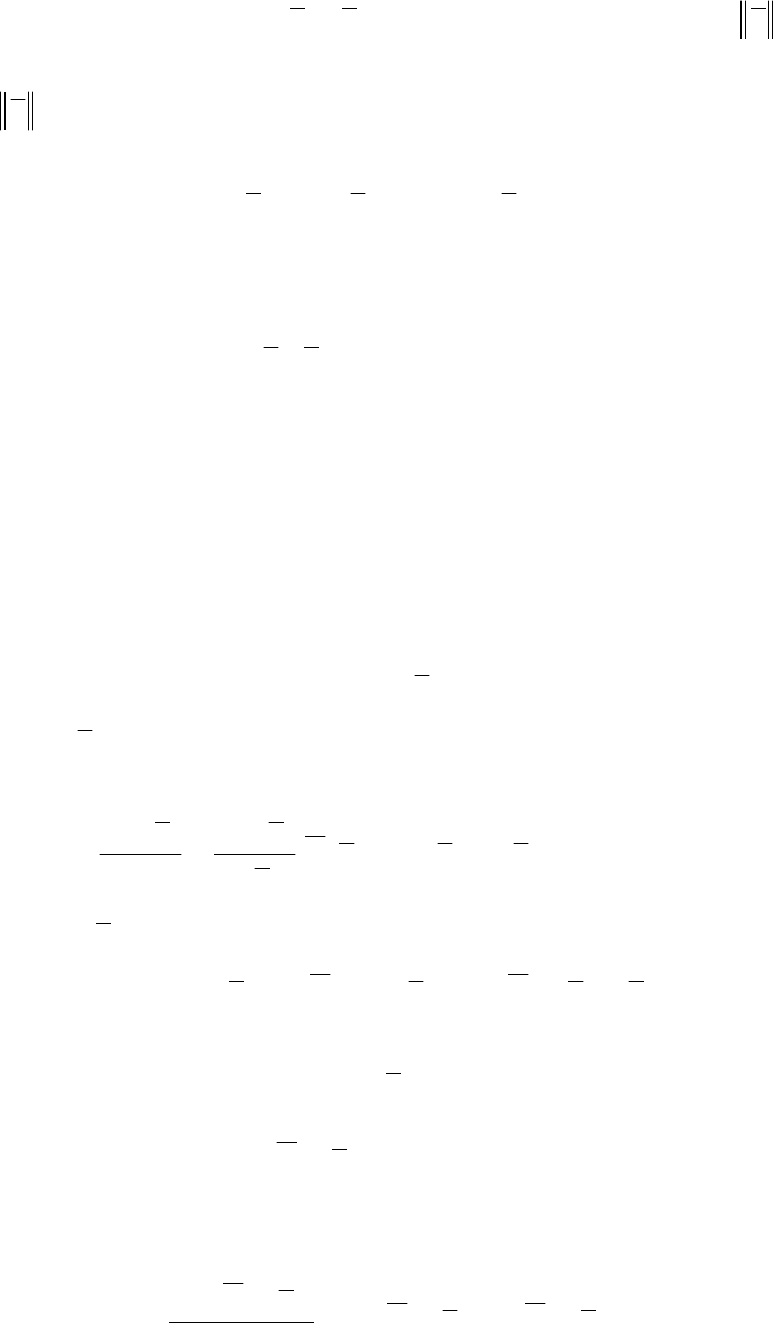
(
)
tyy
=
не попадает в область
ε
<
y
численное решение . При
решение оказывается при некотором t внутри сферы
k
rr =
ε<y
.
Считаем, что найденные точки
(
)
kkkk
xry x
ϕ
+
ϕ
= cos
1
лежа с точностью до величины
sin
2
т (
δ
) на границе области притяже-
ния.
3.
Изменяя векторы
21
, xx
найдем различные плоские сечения об-
ласти притяжения.
8.5.2. ПОСТРОЕНИЕ ФУНКЦИИ ЗУБОВА - ЛЯПУНОВА ДЛЯ
В . Зубов показал, что область притяжения асимптотически
НЕЛИНЕЙНЫХ СИСТЕМ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
.И
устойчивого нулевого решения системы (8.53) определяется нера-
венством
(
)
1
<
yV
,
где
()
yV
- ф нкция Зубова- Ляпунову а, удовлетворяющая уравне-
: нию
() ()
() () ()()()
0 =−=
∂
≡ VyVyWyF
ydt
0;1
∂ yVydV
. (8.54)
Здесь
()
yW
- определенно положительная функци Пусть я.
()
(
)
(
)
(
)
xxRytRty
≡
τ
τ
−
= ,0;,
- решение системы уравнений (8.53) в форме Коши.
Если начальный вектор
x
принадлежит области притяжения,
то
(
)
, xtR 0→
при
t
∞
→
.
Интегрируя по t в пределах от нуля до бесконечности уравне-
ние
()
(
)
()
()
()
))
1, −x
((
,
,
= tRVxtRW
d
t
xtRdV
, (8.55)
173
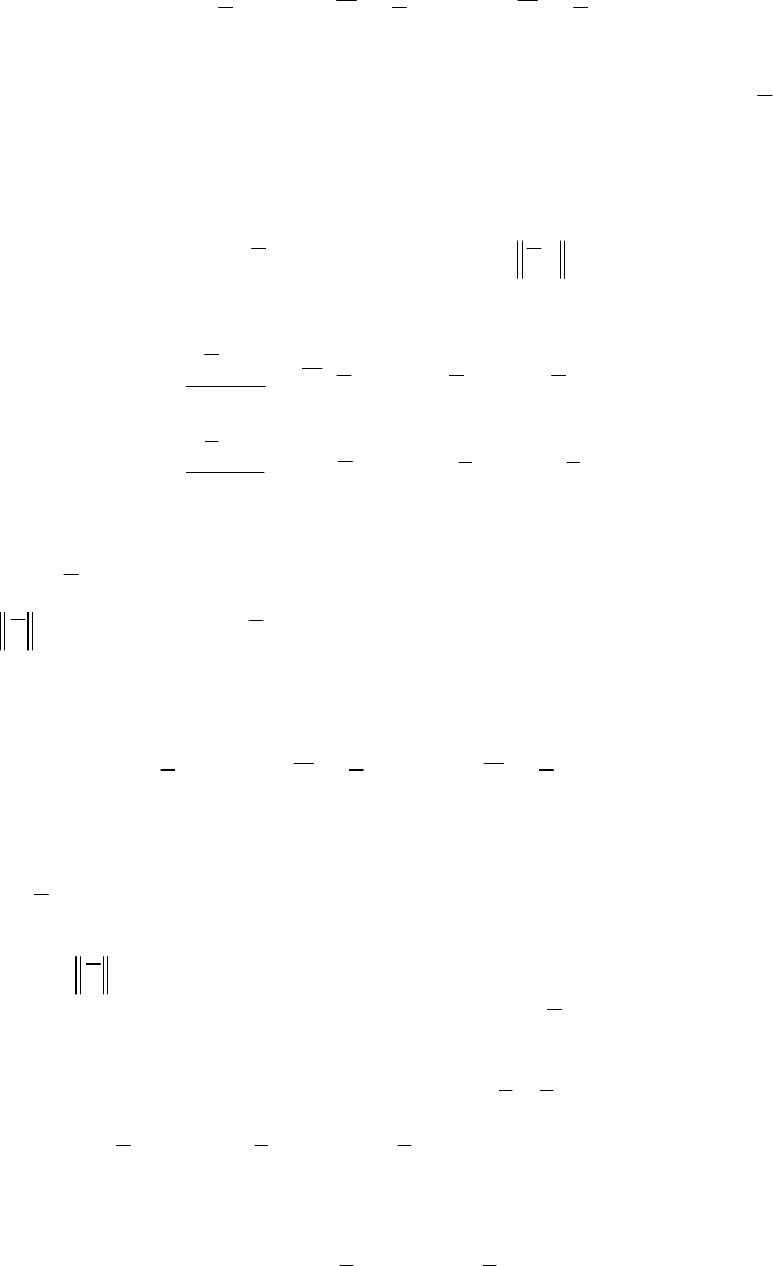
приходим к формуле
() ()
()
()
()
[]
dtxtRVxtRWxV ,1,
0
−=
∫
∞
, (8.56)
которую можно использовать для отыскания функции
()
xV
.
ислит ьный алгоритм.
.
Зад значений
Предлагается следующий выч ел
1 ается набор начальных
()
ρ
<
=
kk
xNkx ,,,2,1 K
.
Ин равн
.
2 тегрируются системы дифференциальных у ений
(
)
()()
()
()() ()
[]
()
,00,1 =−=
kk
k
ztyW
,)0(, ==
k
kkk
tz
d
k
t
tzd
xytyF
dt
на достаточно большом интервале
tyd
[
]
T,0
. Если численное реше-
ние
()
ty
k
при некотором значении
[
]
T,t 0
∈
выходит за область
ρ<y
, то вектор
k
x
исключается из .
3.
И ные выражения
рассмотрения
з формулы (8.56) находим приближен
() ()
()
()
()
[]
()
TzdtxtRVxtRWxV
kk
T
kk
≅−≅
∫
,1,
0
,
из которых можно восстановить функцию Зубова-Ляпунова
()
y
.
V
4.
При
ρ<y
область притяжения асимптотически устойчивого
решения определяется неравенством
(
)
1
<
yV
.
Строим сечение области притяжения плоскостью, проходящей
через точку параллельно векторам
0
z
21
, zz
:
(
)
(
)
qjzzrzy
jj
,2,1sincos
210
K
=
ϕ
+ϕ+=
. (8.57)
При каждом находится такое значение
j
ϕ
j
rr
=
, что
(
)
(
)
1sincos
210
≅
ϕ
+
ϕ
+
jjj
zzrzV
.
174
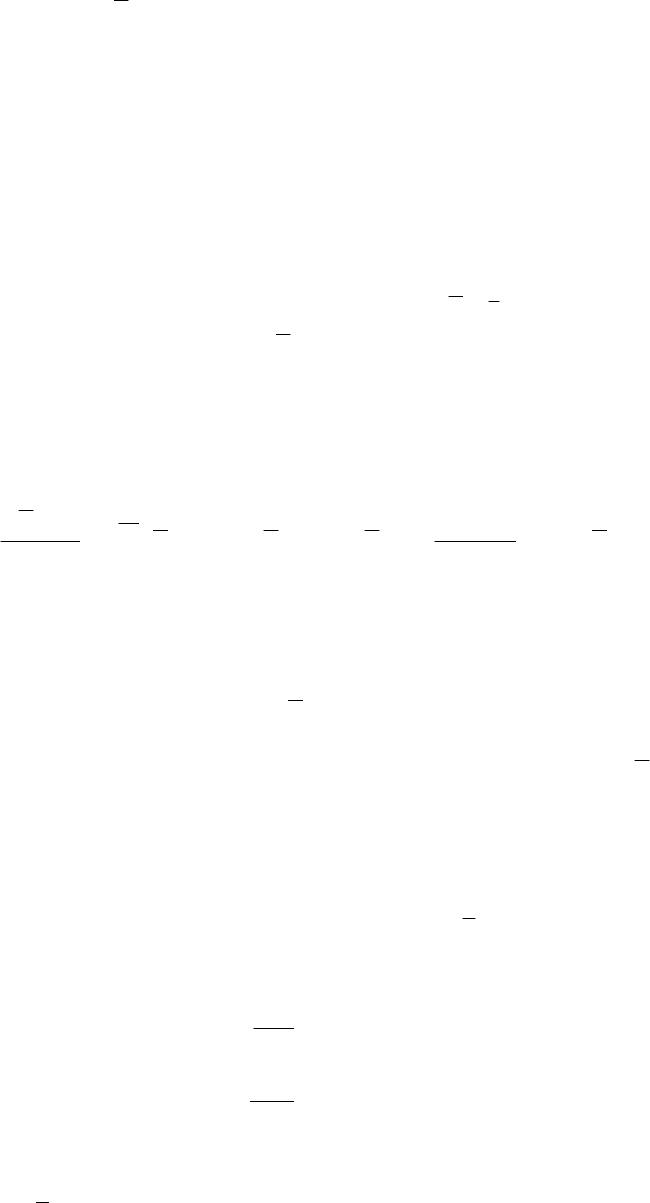
Точка
j
y
, определяемая формулой (8.57), взятой при
j
rr
=
,
це области притяжения. Изменяя значе
лежит на грани ние углов
j
ϕ
,
гра
Интегрируя дифференциальное уравнение (8.55), получаем
формулу
обходим всю ницу сечения области притяжения.
Замечание
∫
∞
− )),(( dtxtRW
()
−=
0
1 exV
, (8.58)
которую можно использовать для нахождения функции Зубова-
Ляпунова. Для этого интегрируются системы дифференциальных
уравнений
()
()() ()
(
)
()()()
00;;0; ====
kk
k
kkk
k
utyW
dt
tdu
xytyF
dt
tyd
на достаточно большом интервале
[
]
T,0
.
В результате получим
(
)
)(
1
Tu
k
k
exV
−
−≅
. (8.59)
ля функции
()
xV
Аналитическое выражение д находится пу-
тем интерполяции численных данных (8.59).
.2
Найдем функцию Зубова-Ляпунова
ПРИМЕР 8
(
)
yV
для дифференциальных
уравнений:
системы
;
3
1
2
2
d
121
1
yyyyy
t
dy
+−+−=
32
2
22121
d
yyyyy
t
dy
+−−−=
.
олучена функция По описанному алгоритму п
(
)
(
)
()
() ( ) ( )
.413461,0153846,0016026,0
25,15,0125,0
4
2
2
1
2
2
4
12
5
1
5
21
66
2
2
2
112
3
1
4
2121
yyyyyyyyyy
yyyyyyyyyyyV
++−++−
−−−++−+=
422 3
2
21
175
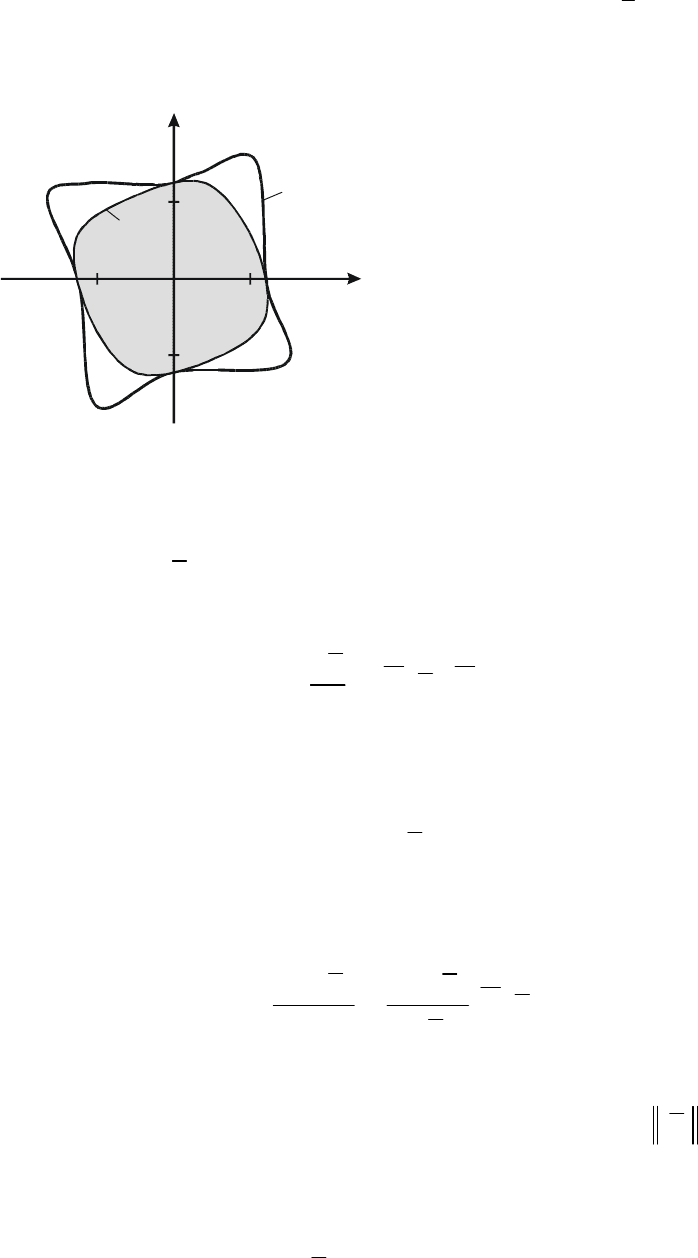
1
1
1
y
-1
1
-1
y
2
0
2
уравнения из примера 8.2:
1 - область, найденная с помощью функции
Зубова-Ляпунова;
2 - точная граница области
Рис 8.8. Области начального отклонения
асимптотически устойчивого нулевого решения
ог
на с помощ
Область притяжения асимптотически устойчивого нулев о решения найде-
ью функции Зубова-Ляпунова из уравнения
(
)
1
=
yV
( с. 8.8)
Для сравнения приведена точ
большую область.
ри
ная граница области притяжения, охватывающая
8.5.3. ПРИБЛИЖЕННОЕ ОПРЕДЕЛЕНИЕ ОБЛАСТИ ПРИТЯЖЕНИЯ
С ПОМОЩЬЮ
Пусть
ФУНКЦИИ ЛЯПУНОВА
()
yV
– определенно поло ункция, найден-
ная для системы нелинейных диффере иа
жительная ф
нц льных уравнений
() ()
00; =Fy
= F
dt
yd
с асимптотически устойчив м ре
Область , определяемая неравенством
ым нулевы шением.
D
(
)
CyV
<
,
будет принадлежать области притяжения, если везде в области
D
выполняется неравенство
()
(
)
()
0<≡ yF
yd
ydV
ydV
.
тот
dt
Э известный результат Ляпунова можно использовать для чис-
ленного построения области
D
, лежащей в шаре
ρ
<
y
.
Вычислительный алгоритм имеет следующий вид:
1.
Выбирается случайный вектор
()
Nky ,,2,1
k
K
=
.
2.
Находится значение такое, что
k
r
176

0)(
)(
=⎜
∂
∂
=
kk
yry
k
yF
y
yV
.
Значения производных находятся численно.
.
Вычисляются значения функции Л3 япунова
(
)
(
)
NkyrVC
kkk
,,2 K,1
=
=
и наименьшее значение
(
)
0min ≥
=
kk
k
CCC
при достаточно большом N.
Таким способом находится граница обл асти
D
с уравнением
()
CyV =
. Чтобы найти точки на границе области , определяем
D
величины
k
ρ
из уравнений
()
(
)
NkCyV
kk
,,2,1 K
=
=
ρ
.
8.5.4. ПУНОВА ЧИСЛЕННОЕ ПОСТРОЕНИЕ ФУНКЦИИ ЛУРЬЕ – ЛЯ
(АБСОЛЮТНАЯ УСТОЙЧИВОСТЬ СИСТЕМЫ НЕЛИНЕЙНЫХ
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ)
Имеем нелинейную систему автоматического управления,
описываемую дифференциальным уравнением
[]
()
σ+= fqyA
d
t
yd
;
(
)
.00; ==σ
∗
fy
(8.60)
где
[A] – вещественная матрица;
d
dq,
– векторы;
(
)
σ
f
– нелинейная функция,
имеющая произвольную нечетно-
симметричную форму (рис. 8.9.).
Функция
(
)
σ
f
удовлетворяет условиям
(
)
0>
σ
σ
f
и определена при всех .
Предполагаем, что система (8.60)
имеет только одну особую точку - нулевую, т.е. система уравнений
f
()
σ
0
σ
Рис 8.9. Нелинейная зависимость
нечетного вида
при
0≠σ
σ
177
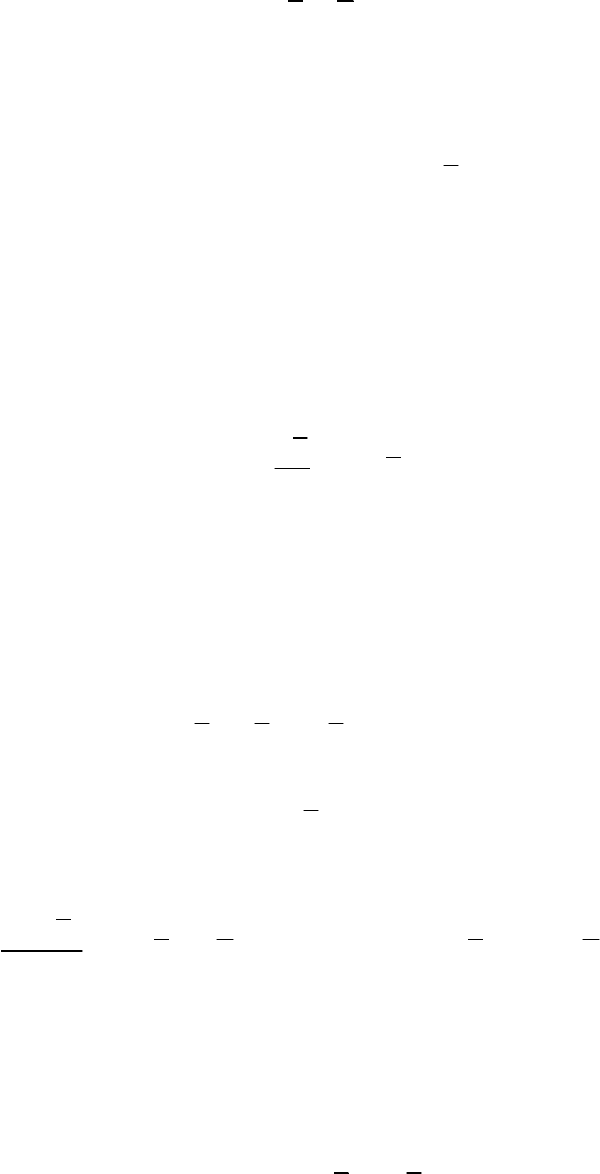
[]
(
)
0
+
σ
=
fqyA
им ре
я,
си устойчивым, а область его
еет лишь нулевое шение.
Ищутся услови при выполнении которых нулевое решение
стемы (8.60) является асимптотически
притяжения является все пространство
y
при любом выборе функ-
ции
()
,σf
удовлетворяющей указанным ограничениям.
Если такие условия выполнены, то система (8.60) называется
абсо
лютно устойчивой.
Необходимым условием абсолютной устойчивости является
устойчивость нулевого решения системы линейных дифференци-
альных уравнений
[]
yA
d
t
yd
=
, (8.61)
т.е. все собственные числа матрицы
[
]
A
имеют отрицательную ве-
унова
щественную часть.
Достаточные условия абсолютной устойчивости устанавли-
ваются с помощью функции Лурье-Ляп
()
[]
()
σσ+=
∫
σ
dfyCyyV
0
*
2
. (8.62)
Дифференцируя функцию
()
yV
в силу системы уравнений (8.60),
получаем после ряда преобразований [11] уравнение
()
()
[] []
()
()
σ+
⎪
⎭
⎪
⎬
⎪
⎩
⎨
σ
⎥
⎦
⎢
⎣
+−=
−
∗
fqAyBfAqy
dt
1
*
, (8.63)
где
[] [][] []
⎭
⎬
⎫
⎩
⎨
⎧
⎥
⎦
⎤
⎢
⎣
⎡
+−=
∗
CAACB
.
Если квадратичная форма
⎫
⎤⎡
−
∗
1
⎪
⎧
ydV
[
]
yBy
*
определенно положительна,
то правая часть равенства (8.63) является определенно отрицатель-
ной функций и нулевое решение системы уравнений (8.60) абсо-
лютно устойчиво.
178

Для того чтобы осуществить синтез абсолютно устойчивой
системы уравнений (8.60) при заданной матрице [A], можно ис-
пользовать следующий вычислительный алгоритм.
1.
Задается определенно положительная квадратичная форма
[]
yBy
*
и решается у я матрицы [C]
.
Из уравнения
равнение Ляпунова дл
[][] [] []
.BCAAC −=
⎥
⎦
⎢
⎣
+
⎤⎡
∗
2
[
]
[
]
qAd
1−
=
находится вектор
C
q
(или вектор
q
d
при заданном векторе при
заданном векторе
d
).
Полученная система уравнений (8.60)
8.6. Т
В отличие от классических задач б устойчивости движения в
формулировке А.М. Ляпунова, функционирование реальных сис-
ем е време
змущающих воздействиях (как начальных, так и
после величи
сти или задач с устойчиво-
тью
Для прикладных задач имеет значение не только факт сущест-
ования допустимого начального отклоне
движения системы
является абсолютно ус-
тойчивой.
ЕХНИЧЕСКАЯ УСТОЙЧИВОСТЬ ДВИЖЕНИЯ
5
о
т происходит на конечном интервал ни, при постоянно
действующих во
дующих) конечной ны.
Задачи с такого рода особенностями получили названия задач
технической (практической) устойчиво
с на конечном интервале времени.
в ния от невозмущенного
0),(
0
>
ε
δ
=δ t
при заданных и , но и
сти оц
0>ε
0
t
оценка этих чисел, проверка пригодно енок в конкретных ус-
ловиях задачи. Поэтому основными следует считать те методы ре-
шения задач устойчивости, которые дают возможность получения
указанных результатов.
5
Этот параграф написан канд. физ. мат. наук А.П. Тарасовым.
179
