Афанасьев А.А. Математические основы теории систем управления
Подождите немного. Документ загружается.


4. Если система асимптотически устойчива целом при любом
ленного класса нели-
нейностей), то она называется абсолютно устойчивой.
в
характере нелинейности (в пределах опреде
8.2 ЗНАКОПОСТОЯННЫЕ И ЗНАКООПРЕДЕЛЕННЫЕ
ФУНКЦИИ
Рассмотрим скалярную функцию
()
(
)
ytVyyytVV
n
,,,,
21
=
= K
,
определенную и непрерывную в области
G
Hyta
<
∞
<< ,
(8.5)
в этой области непрерывными частными производ-
ными по и обращающуюся в нуль при
и обладающую
n
yyyt ,,,,
21
K
0=y
:
(
)
00,
=
= tVV
.
Функци этого вида используется при анализе устойчивости
неавтономных уравнений типа (8.4).
Рассматриваемая функция может не
я
зависеть явно от времени
()
yVV =
,
(
)
00
=
=
VV
.
Она используется при анализе устойчивости автономных уравне-
ний.
Рассмотрим некоторые определения.
.
Ес
1 ли в области
G
функция
V
сохраняет один и тот же знак, но
обращается в нуль не только в начале координат, то такая функ-
ция называется знакопостоянной или знакополуопределенной
(положительной или отрицательной).
Например, функция
()
(
)
2
2
yyV +=
1
yV =
является знакоположительной или полуопределенно положитель-
ной, т.к. она обращается в нуль на прямой
21
yy
−
=
.
()
yV
2. Функция называется определенно положительной (строго
положительной) в области , если
G
150

()
0>yV
при
(
)
(
)
000
=
≠
Vy
.
Такая функция, например, может иметь вид
(
)
2
33
2
22
2
11
yayayayVV ++==
.
.
Функция
(
)
yV
называется определенно отриц
от ти
ательной (строго 3
рицательной) в облас если функция -
G
,
()
yV
является оп-
ределенно положительной.
()
ytV ,
4. Функция называется определенно положительной в об-
ласти , если существует определенно
ржа я времени функция
G
ща
положительная, не со-
(
)
yV
1
де такая, что будет выполняться
неравенство
(
)
(
)
yVytV
1
, ≥
.
Пример:
()
yyytV ,
22
++=
(
)
21
2
2
2
11
yyyyyV −+=tyy sin
212
;
1
.
5.
Функция
()
yt,
называется определенно отрицательной, если
функция
V
()
ytV ,−
является определенно положительной. Опре-
деленно положительные или определенно отрицательные функ-
ции называются знакоопределенными.
.
Если функция
()
ytV ,
в любой окрестности нач
может принимать значения разных знаков, то она называется
знакопеременной. Например,
ала координат 6
(
)
tyyytV sin,
21
=
.
Рассмотренные функции
V
от к наоорди т состояния системы,
В общем случае суждение о знакопостоянстве или знакоопре-
обращающиеся в нуль в начале координат, играют важную роль в
теоремах Ляпунова об устойчивости движения и называется функ-
циями Ляпунова.
деленности функций
(
)
ytV ,
или
(
)
yV
представляет собой сложную
задачу.
Достаточно просто знакоопределенност находится в том слу-
чае, если функции Ляпунова представляют квадратичные формы:
ь
151

()
[]
∑
==
jiij
T
yycyCyyV
, (8.6
=
n
ji
,
)
1
() ()
[]
()
∑
=
==
ji
jiij
T
yytcytCyytV
1,
,
. (8.7)
Если коэффициенты
()
tC
квадратичной формы ограничены
при
0
tt ≥
, то она удовлетворяет
0
t≥
неравенству
n
при
t
(
)
yyytVyy
21
, λ≤≤λ
, .8
TT
(8 )
де
г
const,
1 2
=
λ
λ
.
рма (8.7) с огра
фициентами положительной
Квадратичная фо ниченными при коэф-
будет определенно , если удовлетворя-
м Сильв с
0
tt ≥
ет условия е тра:
(
)
[
]
t–
Все главные
1
диагональные миноры матрицы строго поло-
жительны
()
(
)
(
)
() ()
()
()
() ()
.0
;00
2
22
1211
111
>α
>α≥>α≥
n
tctc
tctc
tc
K
K
(8.9)
остаточны для определенной по-
ы
;
1
111
21
≥
nnn
n
tctc
tctc
K
KK
K
K
Эти условия необходимы и д
(
)
ytV ,
ложительности квадратичной форм .
.9) существует определенно по-
а
При выполнении условий (8
ложительная, не зависящая от времени квадратичная форм
()
[
]
yCyyV
T
11
=
,
такая, что при
0
tt ≥
справедливо неравенство
()
(
)
yy
T
α≥
1
,
yVytV ≥,
1
Главным диагональным минором порядка
k
матрицы
[
]
)(tC называется ми
нор, составленный из первых
k строк и первых k столбцов матрицы
[]
)(tC
.
-
152
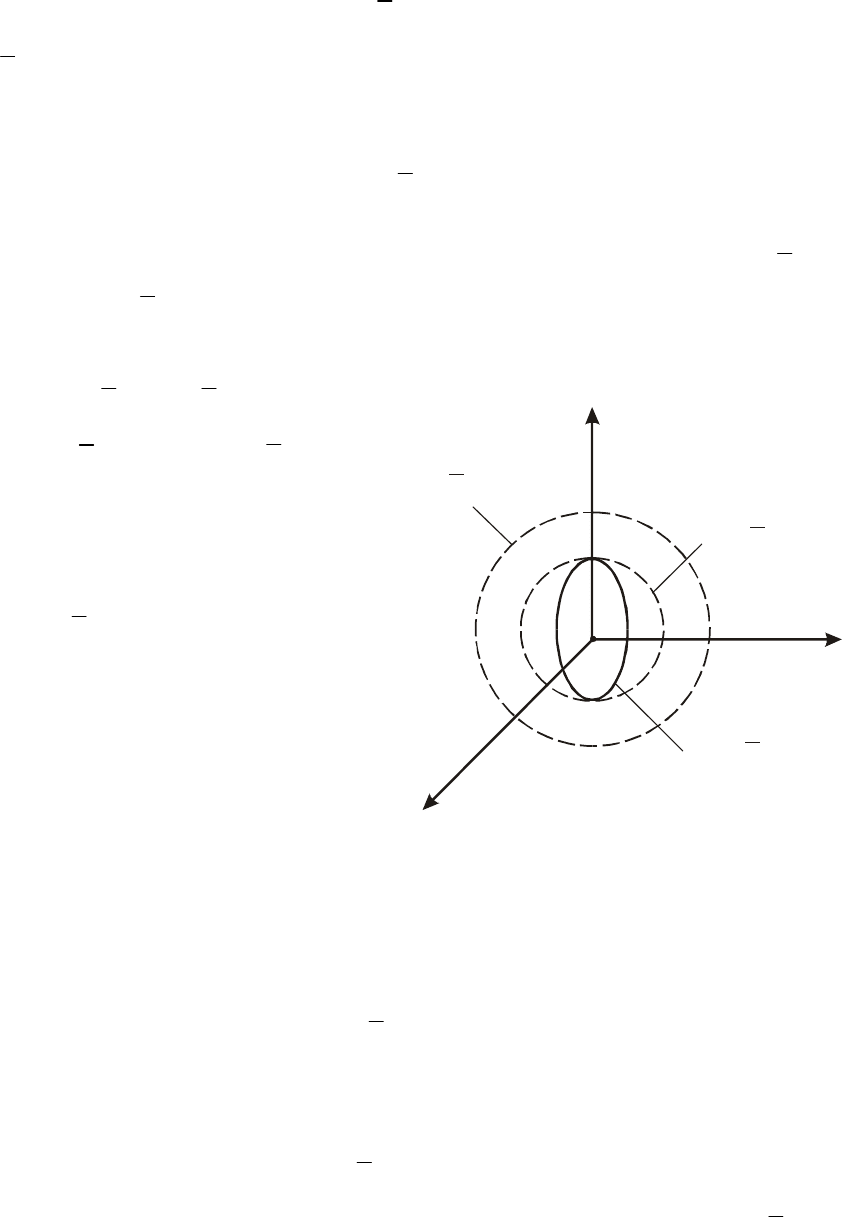
где .
чивости рассматривается поведение функций
0>α
В теории устой
(
)
(
)
tytV ,
,
г де
()
ty
- решение системы дифференциальных уравнений в от-
клонениях (8.4). На основании свойств этих функций делаются за-
лючения о поведении решений системы (8.4). к Именно при такой
(
)
ytV ,
трактовке аргумента функции она и будет называться
цией Ляпунова.
Рассмотрим
функ-
геометрическую иллюстрацию функции
(
)
ytV ,
.
Пусть
(
)
ytV ,
- положительно определенная ( положи-
тельная) функция, такая, что
строго
() ()
yVytV
1
, ≥
, (8.10)
где
()
> 0
1
yV
при
0
≠
y
и
.
Предположим, что поверхности
ня
()
00
1
=V
уров
() (
0
1
≥> ccyV
в пространстве пред-
ставляют собой семейство не-
прерывных замкнутых поверхно-
тей,
динат О и монотонно расши-
, на рис. 8.3 они показаны
огда, очев
yy
3n
,...
)
n
yy ,,
1
K
с окружающих начало коор-
ряющихся при росте параметра с.
Будучи вложенными в друг
друга
пунктиром. Т идно, каждая поверхность уровня
(
)
1
, cytV
=
для любого значения времени t будет целиком располагаться внут-
ри соответствующей поверхности
(
)
11
cyV
=
.
Здесь нужно иметь в виду, что при одинаковых значениях
y
вы-
еравен во (8.10), поэтому для обеспечения равенства полняется н ст
y
1
y
2
V( )=c
12
y
0
V(t, )=cy
1
V( )=c
11
y
Р
ис.8.3. Вложенные др
у
г в др
у
га
хности уровня строго
ложительных функций Ляпунова
повер
по
cc
>
21
153
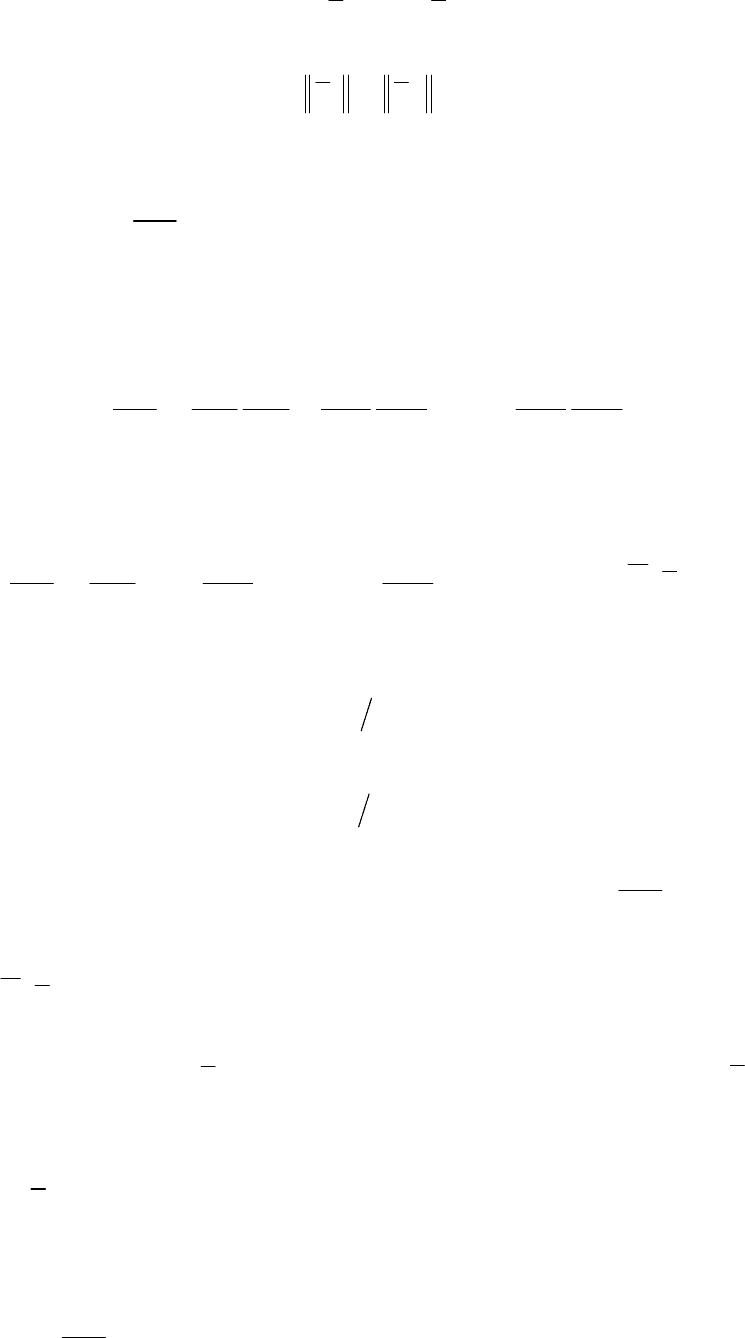
()
(
)
21
, yVytV
=
необходимо иметь
21
yy
≤
.
Пусть имеется автономная нелинейная система
()
niyyyF
dt
dy
ni
i
,,2,1,,
21
KK ==
. (8.11)
Производная по времени от знаковой функции
будет иметь вид
()
n
yyyV K
21
,
dt
dy
y
V
dt
dy
y
V
dt
dy
y
V
dt
n
n
∂
∂
++
∂
∂
∂
=
K
2
21
.
В силу уравнений системы (8.11) получим
dV
∂
+
1
()
)(
21
yFgradVF
V
F
V
F
VdV
n
⋅=
∂
21
yyydt
n
∂
++
∂
∂
+
∂
∂
= K
, (8.12)
где
⎥
⎥
⎥⎢
⎦
⎤
⎢
⎡
∂
∂
∂
⎢
⎣
∂
=gradV
M
1
- вект
n
y
yV
ор.
производная
V
Формула (8.12) показывает, что
d
t
dV
представля-
ет скалярное произведение вектора
V
grad
на вектор фазовой ско-
рости
()
yF
изображающей точки
M
в фазовом пространстве (рис.
.4).
Вектор
8
(
)
yVgrad
перпендикулярен поверхности
()
cyV =
и
вознаправлен в сторону растания значения
V
. В точке
1
M
, где фа-
ктория пересекает поверхностьзовая трае в возрас-
тания
уровня сторону
()
yV
, скалярное произведение векторов (8.12) положительно
(скалярное произведение равно произведению модулей векторов на
косинус угла между ними). Следовательно, этой траекто-
рии имеем
точки для
0>
dt
dV
.
154

y
В точке
2
M
фазовая траектория пересекает поверхность уров-
ня в сторону уменьшения
(
)
yV
.
ведение (8.12) отрицательно (уг
торами тупой Следовательно, в
Видим, что здесь скалярное произ-
ол между рассматриваемыми век-
этой точке имеем ).
0<dtdV
.
Функция Ляпунова
(
)
ytV ,
будет иметь производную по -
мени в силу неавтономной системы
ем
вре
(8.4), определяемую выражени-
()
),( ytFradV ⋅g
t
V
dt
dV
+
∂
∂
=
Так же как и для автономной сис если
. (8.13)
темы,
0>
dt
dV
при
(
)
(
)
0, >
=
ccyt
,
V
то фазовая траектория
(
)
ty
в точках
y
t
,
поверхности
()
cytV
=
,
пе-
ресекает ее (без касания, скольжения вдоль ее) в направлении роста
()
yt,V
.
При
0
<
dtdV
фазовая траектория
()
ty
при росте t пересекает поверхность уровня
()
cytV =,
в сторону уменьшения с [16].
1
y
2
yy
3n
,...
grad V
Рис.8.4. Скалярное произведение векторов
ешения а
нелинейной системы (8.11):
()- вектор фазовой скорости;
grad V - векто градиента функции Ляпунова
Fy
M
0
1
M
2
0
M
Fy
()
Fy
()
в точках и
фазовой траектории р втономной
dt
dV
yFVgrad
=⋅
))((
)0(
1
>
dt
dV
M
)0(
2
<
dt
dV
M
р
155
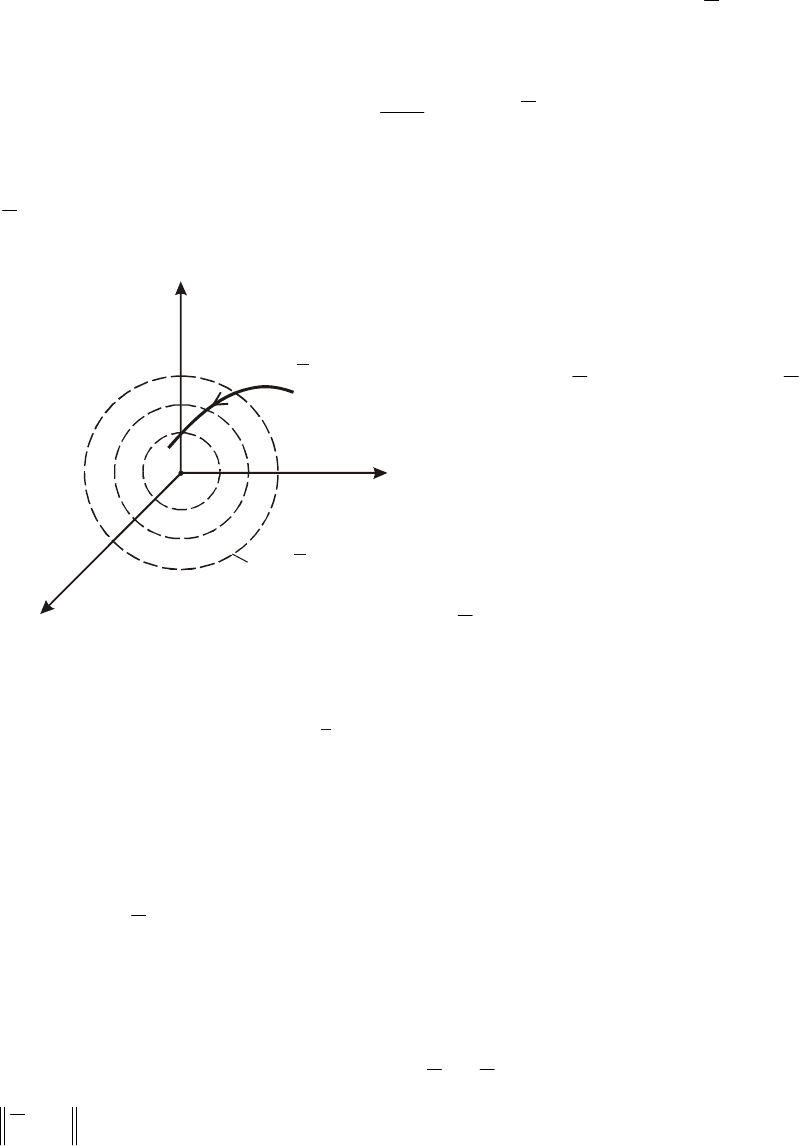
8.3.ТЕОРЕМЫ ЛЯПУНОВА
ПЕРВАЯ ТЕО ОВА (ТЕОРЕМА ОБ УСТОЙЧИВОСТИ)
(8.4) сущест-
кция
РЕМА ЛЯПУН
Если для неавтономной системы в отклонениях
вует определенно положительная фун
(
)
ytV ,
, производная
которой в силу системы
()
ytW
dt
,
является знако ца
dV
=
отри тельной функцией, то решение системы
0=y
устойчиво.
метрическая иллюстрация
дается на рис.8.5.
Гео
этой теоремы
При
(
)
0, >yt
и
V
(
)
0, ≤ytW
,
в
рхн
(если
соответствии с предыдущим, фа-
пере
ости у трь,
поверхности
зовая траектория секает по-
ве ровня извне вовну
или скользит по этой
0
=
W
). Поэтому решение
(
)
ty
остается ограниченным. (Речь
а не
иво-
име
нова ости
идет просто об устойчивости,
об асимптотической устойч
сти).
Аналогичную формулировку
ет теорема и применительно к
автономным системам.
Теорема Ляпу дает достаточные условия устойчив
решения
0=y
нелинейной системы. Поэтому система может быть
устойчивой и за предел х условий. Насколько полно условия
теоремы охватят действительную область устойчивости системы
зави от выбора функции Ляпунова.
Рассмотрим решение
ами эти
сит
(
)
tyy
=
с начальным условием
()
δ<
. 8.6). тория этого решения
0
ty
(рис Согласно теореме траек
y
yy
,...,
1
3n
ccc
123
<<
y
()
t
0
y
2
c
1
c
2
Vt c
(, )=
y
3
Рис.8.5. Фазовая
усто
уравне
извне
траектория
йчивого решения неавтономного
ния состояния (8.4) пересекает
поверхность уровня V(t, )=c или
скользит по ней
y
156
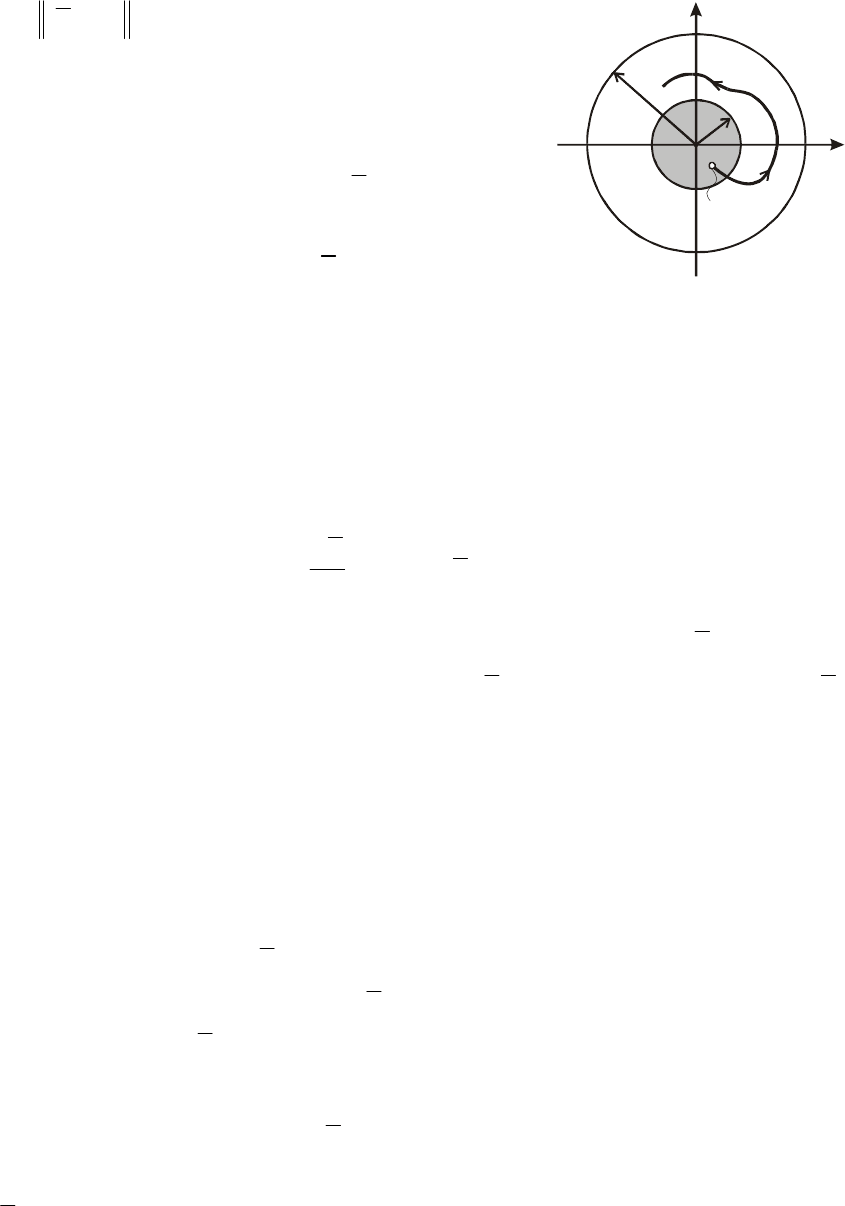
должна остаться целиком внутри сферы радиуса
δ>ε
(для фикси-
рованного
0>ε
существует вполне определенное
δ
, т.е.
(
)
ε
δ
=δ
)
()
y
1
y
n
0
yt
()
0
ε<ty
при
0
∞
<
≤
tt
. (8
0
.14)
При наличии условий первой тео-
ремы Ляпунова все решения
Следствие 1
ε
δ
Рис.8.6. ог о
ой ре и
началь
(
)
t
y
систе-
начальными значениями
мы (8.4) с достаточно малыми по норме
(
)
нечно продолжаемы вправо
ы на
Следствие 2
0
ty
беско-
и ограниче-
Сферы
чивого)
ного отк
раниченног
шения
лонения >0
ε>0
δ
н полуоси
[
)
∞,
0
t
.
(уст
Если для линейной однородной системы
()
[]
ytA
yd
=
dt
15) (8.
существует определенно положительная функция
()
ytV ,
, для кото-
р роизво ная в силу системы ой п д
(
)
0,
≤
ytW
, то все решения
(
)
ty
(8.15) определены и ограничены на полуоси
[
)
∞,
0
t
системы
(ТЕОРЕМА ОБ АСИМПТОТИЧЕСКОЙ
Пусть для системы (8.4) существует -
.
)
положи
ВТОРАЯ ТЕОРЕМА ЛЯПУНОВА
УСТОЙЧИВОСТИ
определенно
(
тельная функция
)
, имеющая определе трицательную
производную по врем
ytV ,
нн
ени
о о
(
)
,
<
0ytW
в силу этой систем гда
решение системы
ы. То
0=y
устойчивым
Услови
будет асимптотически
я этой теоремы отличаются от
ем,
.
предыдущейусловий
т что производная
(
)
ytW ,
является трицательной, а
определенно отриц функцией. Поэтому фазовая траекто-
рия
не знак
ательной
оо
()
ty
, пересекая поверхности уровня
const
=
V
извне внутрь, не
157
может остаться на них, пой лоть до начала координат,
де
дет внутрь вп
0=
и
()
00, =tV
. Следователь еем г
y
но, им
()
0→ty
при
∞
→
t
.
Эта и первая условия устой-
чивости, и охвата ой области устойчивости
и Ляп
, дает достаточные
действительн
теорема, как
полнота
зависит от выбора функци унова
(
)
ytV ,
.
Следствие 1
В теоремы множество условиях второй Ляпунова
∞
≤
<
≤
Hhy
принадлежит области притяжения решения
0
=
y
.
Следствие 2
Если однородной системы для линейной
()
[]
ytA
dt
yd
=
существует определенно положительная функция
),( y
t
V
, удов
яющая условиям второй теоремы Ляпунова, то каждое реш
й системы асимптотически устойчиво в целом.
ле-
твор е-
ние это
Пусть системы уравнений (8.4) существует функция
ТРЕТЬЯ ТЕОРЕМА ЛЯПУНОВА (ТЕОРЕМА О НЕУСТОЙЧИВОСТИ)
для
()
ytV
производной
,
, определенно-знаковойобладающая
()
ytW ,
в
силу системы.
Если в любой сколь угодно малой окрестности начала коорди-
нат
(
)
Hhy
<
≤
Δ
Δ<
найдется точка
()
00
, yt
, для которой знак
(
)
ytV ,
совпадает со
()
ytW
знаком производной
dt
dV
,=
, то решение системы
0=y
не-
устойчиво.
158

(
)
0, >ytV
Допустим для определенности, что , тогда
ой точке имеем
в некото-
р
()
0, >ytW
, т.е. в этой точке, в со
улой (8
ответствии с
форм .12), фазовая скорость направлена от начала коорди-
нат. Система расходится.
Замечание 1
В третьей теореме функция
(
)
ytV ,
не обязательно является
определенно-знаковой.
Замечание 2
Функции Ляпунова
(
)
ytV ,
, удовлетворяющие условиям пер-
вой, второй и третьей теорем Ляпунова, будем называть соответ-
ственно функциями Ляпунова 1-го, 2-го и 3-го рода.
Если для системы дифференциальных уравнений (8.4) суще-
функция Ляпунова 1-го, или 2-го, или 3-
той системы
Следствие
ствует го рода, то решение
э
0=y
соответственно устойчиво
пунову при
, неустойчиво по Ля-
∞→
t
.
ВА
ЛЯПУНОВА С ПОМОЩЬЮ
ПОСЛЕДОВАТЕЛЬНЫХ РЕШЕНИЙ ИСХОДНОЙ СИСТЕМЫ
Имеем исходную систему нелинейных дифференциальных
8.4. ЧИСЛЕННОЕ ПОСТРОЕНИЕ ФУНКЦИЙ ЛЯПУНО
8.4.1. ПОСТРОЕНИЕ ФУНКЦИЙ
НЕЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
уравнений в отклонениях
() ()
00,;, == tFytF
dt
yd
, (8.16)
в области
G
которая имеет
0, ≥
<
tHy
асимптотически устойчивое решение.
Пусть известно решение системы (8.16) в форме Коши
159
