Афанасьев А.А. Математические основы теории систем управления

Подождите немного. Документ загружается.

История создания теории технической устойчивости и реше-

ния, связанных с ней проблем, имеют много аналогий с историей

вопрос был м

технич

ие

ости в смысле Ляпунова, когда

вопрос устойчивости или и не зависит от выбора

формы и размеров этих об в вопросах технической

разли

тей д

Пос

Рассмотрим нелинейн возмущенные движения ко-

торых в области

теории устойчивости в смысле Ляпунова. Впервые, видимо, этот

рассмотрен Н.Г. Четаевым [54], а в дальнейше в рабо-

тах и других авторов. Обзор наиболее существенных идей в этой

области можно найти в работе К.А. Абгаряна [1]. В ней же отмече-

но, что в задачах еской устойчивости имеет существенное

значен выбор формы и размеров областей допустимых состоя-

ний, в отличие от задачи устойчив

неустойчивост

ластей. Поэтому

устойчивости важны разработки чных критериев и условий,

решающих один и тот же вопрос относительно разных форм облас-

опустимых состояний.

тановка задачи

ые системы,

{

}

∞<<= TstsxtxS

,;,,

***

(8.64)

описываются системой из n обыкновенных дифференциальных

уравнений первого порядка:

≤≤ Tt

(

,tF

)

(8.65)

где

– n–мерный вектор рдинат арактеризующий

движения

фазовых коо , х

отклонение от программного ;

()

xtF ,

– n–мерная вектор-функция, удовлетворяющая в облас-

ти (8.64) условиям теоремы существования и единствен-

ности решений, а такж е

(

)

.00,

(

)

≡

В силу последнего условия вектор является решением

системы (8.65).

Нулевое решение

()

0≡tx

системы (8.65) называется невоз-

ями.

мущенным движением, а все другие решения, отличные от нулево-

го, будут возмущенными движени

180

Наряду с системой (8.65) в области (8.64) трим систему рассмо

() ()

,,, xtRxtF

(8.66)

в которой n–мерная вектор-функция

(

)

xtR ,

учитывает постоянно

действующие возмущения, удовлетворяет условиям теоремы суще-

ствования и единственности решений системы (8.66) и допустимые

значения

()

принадлежа му ограниченному подмно-

фазовом ространстве координат

определены некоторая ограниченная область , неиз-

бласть

xtR ,

т некоторо

жеству

()

n–мерного евклидового пространства

, содержащему

начало координат.

Пусть в n–мерном п

менная во времени, и ограниченная о

xxx K,,

(

)

, вообще говоря,

по t.

еняемая

(

)

tSS ,

изм содержат внутри себя начало координат.

Через

()

обозначим возмущенное движение удов-

ьному

системы (8.65),

летворяющее начал словию

(

)

Определение 1.

Невозмущенное движение

(

)

≡

системы (8.65) называется

нически устойчивым

, если всякое возмущенное движение

тех на заданном конечном интервале времени

[]

Tt ,

(

)

, определенное на-

()

Stx

∈

, удовлетворяет условию альным условием

для любого

[

]

Ttt ,

∈

()

Stx ∈

Определение 2.

Невозмущенное движение

(

)

≡

системы (8.65) называется

технически устойчивым на заданном конечном интервале времени

при наличии постоянно действующих возмущений

[

Tt ,

]

(

)

xtR ,

если любое решение

()

системы (8.66), определенное начальным

условием

()

000

Sxtx ∈=

, при любых

(

)

(

)

trxtR

∈

у рдовлетво яет ус-

юлови

для любого

[

]

Ttt ,

∈

()

(

)

tStx ∈

Способы задания областей

(

)

(

)

SS rt

определяют то или

иное конкретное содержание понятия устойчивости. Например, ес-

181

л ри заданных конечных и х постоянных и п положительны

(

)

,, sCC <≤εγε

допустимые состояния определить в виде

{

}

(

)

{

}

() () ()

{}

,,,

γ≤

≤==ε≤

xtRxtR

CxxStSxx

следуя Н.Г. Четаеву [54], устойчивость в смысле

называют

этом случае,

определения 1 иногда

то в

{

}

TtC ,,,

– устойчивостью, а ус-

тойчивость в смысле определения 2

{

}

TtC ,,,,

– устойчиво-

функций Ляпунова является основным ме-

(8.65) существует положительно опреде-

стью.

Посколько метод

Если для системы

ленная в

функция

тодом исследования и в задачах технической устойчивости, то при-

ведем одну из теорем в этой области для случая, когда формы об-

ластей допустимых возмущений заданы в виде замкнутых n - мер-

ных шаров [47].

Теорема.

()

[

]

TttxtV ,,

∈

положительнаяи нта

, что

()

конста

()

{

}

111

, SCxtVxtG

⊂≤=

; (8.67)

2) в

при любом

[]

Ttt ,

∈

производная

() ()

()

(

)

≤

∂

∑

xtV

xtF

xtdV

; (8.68)

()

12020

CCtGS

⊂

(8.69)

то невозмущенное движение

(

)

≡

системы (8.65) –

устойчиво.

Доказательство.

{}

TtC ,,,

Пусть утверждение теоремы неверно, т.е. условия теоремы

выполняются, но существует момент времени , что

[]

Ttt ,

∈

182

183

()

Stx ∈

. Тогда в сил ния системы (8.65) и

условия (8.67) существует

у непрерывности реше

, что

()()

(

)

(

)

1122

,,, ctxtVctxtV

для любых

[]

,ttt ∈

– моментт.е.

первого пересечения траектории

()

с поверхно

стью

(

)

(

)

, ctxtV

Из условия (8.69) имеет место

(

)

(

)

, ctxtV

100

. Теперь, интег-

рируя (8.68) на решениях системы (8.65) в пределах от

до

, по-

лучим

()() ()()

(

)

(

)

≤=

∫

txtdV

022

− tVtxtV

или

(

))(

(

))

12200

, ctxtV, txtV

≥

то противоречит п ше неравенству ч олученному вы

(

)

(

)

100

, ctxtV

Следуя Н.Ф. Кириченко [24], можно показать обратимость

этой теоремы. Но тем не менее, в общем случае, ценность этой тео-

ремы ограничена отсутствием онструктивности пост

ции

к роения функ-

()

xtV ,

, удовлетворяющей условиям (8.67)–(8.69). Для частного

вида системы (8.65) в классе ф о ви-

да

ункций Ляпунова квадратичног

(

)

xxxV

вышеприведенная теорема приобретает конструктивное

ние [47].

К задаче о – ус йчи

сти) близки задачи техническо бесконечном ин-

тервале времени, ограниченности решений систем диффе

уравнений, оценки точности приближенных интегрирований.

содержа-

{}

TtC ,,,

то вости (технической устойчиво-

й устойчивости на

ренциаль-

ных

ГЛАВА ДЕВЯТАЯ

ЧАСТОТНЫЙ КРИТЕРИЙ АБСОЛЮТНОЙ

УСТОЙЧИ

(КРИТЕРИЙ В.М.ПОПОВА)

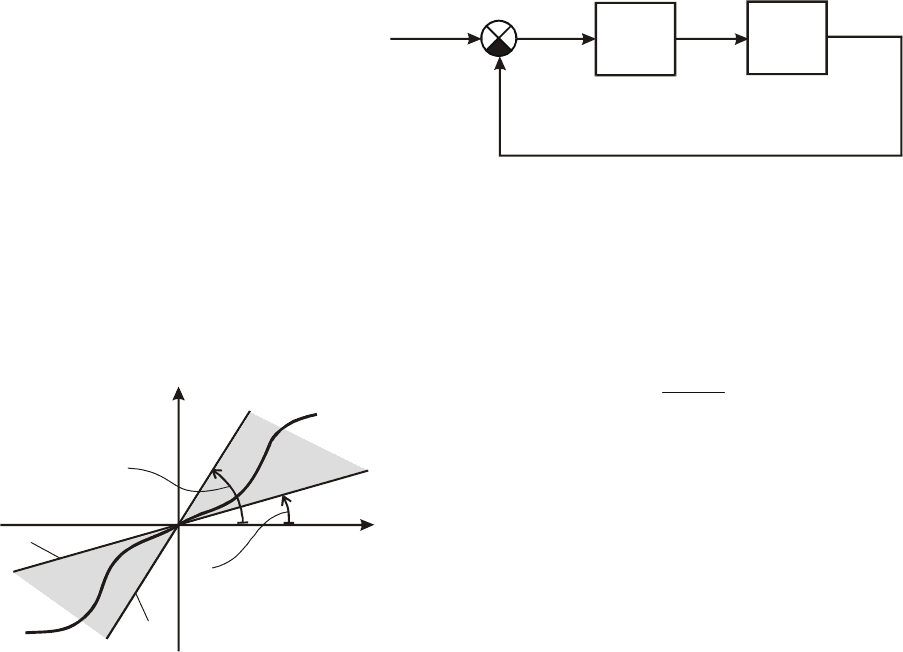
Рассмотрим нелинейные системы, труктурная схема которых

ВОСТИ НЕЛИНЕЙНЫХ СИСТЕМ

9.1. ПОНЯТИЕ АБСОЛЮТНОЙ УСТОЙЧИВОСТИ

может быть приведена к ви-

ду рис.9.1.

Схема содержит одно

нелинейное

безынерционное нелиней-

ное звено с однозначной ха-

рактеристикой

)(

y Φ=

(9.1)

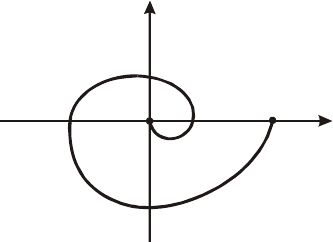
нечетного вида, проходящей через начало координат (рис.9.2), и

линейную часть с передаточной функцией

)(

sW =

, (9.2)

причем степень многочлена

( )

больше с ни многочлена

)(

тепе

В соответствии со схемой

1. меем для ошибки системы рис.9. и

)()()(

−

. (9.3)

Переходя к изображениям по

, получим:

Лапласу

)()()()(

−

, (9.4)

где

[

]

{

}

)()( txLsY

Если уравнение (9.4) перевес еменную область, то бу-

дем иметь

ти во вр

звено

линейная

часть

Ф()

()

Рис. 9.1. Канонический вид структурной схемы

нелинейной системы

Ф()

=arctg

Рис. 9.2. Нелинейная функция внутри

углового сектора с линейными

границами

184

τ−−=

∫

dtktgtx )()()(

, (9.5

[]

τΦτ x()

)

де

[

]

1−

)()( sWLt =

- импульсная (весовая) функция линейной час-

ти системы.

Уравнение (9.5) показывает, что нелинейная система может

быть выведена из состояния равновесия изменением либо внешне-

)(

, либо начальных условий го воздействия

00 =τ

Если внешнее воздействие отсутствует

)( ⎜τ= xx

)0)(( =

, то уравне-

(9.5) ние имеет тривиальное решение

0)(

≡

которое соответствует положению равновесия.

Будем рассматривать систему при таких воздействиях, кото-

рые ограничены по модулю и являются исчезающими функциями

времени.

Обозначим максимальное воздействие

)()(Sup supremumtg

рассматривая его не в смысле амплитуды функции, а в смысле

функционала, т.е. такого воздействия, которое приведет к макси-

мальному отклонению координаты

от равновесного состояния.

)(

Исчезающей функцией времени называется функция,

стремящаяся с течением времени к нулю

0)(lim

→

Положение равновесия устойчиво по Ляпунову, если при мак-

льном внсима ешнем воздействии

)()( tftgSup

имеет место неравенство

≤

∞→

)(lim tx

сколь угодно малое положгде – ительное число.

В зависимости от значения

)(Sup tg

различают три вида ус-

тойчивости:

185

1 тойчивость в малом, если – ус

)(Sup tg

бесконечно мало;

2 – устойчивость в большом, если

)(Sup tg

– конечная величина;

3 – устойчивость в целом, если

)(Sup tg

не ограничено.

Устойчивость в целом может включать

ывают устойчивость

оложения равновесия в целом, имеющую м

в себя абсолютную ус-

тойчивость. Абсолютной устойчивостью наз

п есто для характеристик

)(

еленному классу. , принадлежащих к какому-либо опред

9.2. КРИТЕРИЙ ПОПОВА ДЛЯ СЛУЧАЯ

xkx <

)Φ(

Будем полагать, чт йная чо лине асть системы устойчива, т.е.

корни полинома

)(

лежат в левой полуплоскости (допускается

наличие не более двух нулевых корней).

9.2.1. ТЕОРЕМА ПОПОВА

Теорема Попова имеет следующую формулиров (доказа-

тельство см. в [51]).

Дл

ку

я того чтобы положение равновесия нелинейной системы с

устойчивой линейной частью было абсолютно устойчивым, дос-

таточно, чтобы пр всех

0≥ω

выполнялись следующие неравенст-

ва:

,)(0

)()1(Re)(Re

jWhjj

⎥

⎦

⎤

⎢

⎣

⎡

+ωω+=ω

∏

(9.6)

<Φ<

где - функция Попова;

h - некоторое дейст

рое может прини с

()

∏

ωj

вительное (вещественное) число, кото-

мать я произвольным;

)( ω

- амплитудн ная хара

линейной части си

Для обоснования графичес

лютной устойчивости Попова

ная характеристика линейн

о-фазовая частот ктеристика

стемы.

го представко ления критерия абсо-

вводится модифицированная частот-

ой части

186

()

()( ω+ω=ω )

∗

jVUW

, (9.7)

терист

которая связана с частотной харак ико

(

)

)()(

jVUjW

(9.8)

следующими равенствами:

).((),()( ωω=ωω=ω )

∗

VVUU

(9.9)

Обратим внимание на некоторые особенности модифициро-

ванной характеристики

)( ω

∗

[13].

Если лителя передаточной функции (9.2) не выше

степен ля и если она не имеет полюсов в начале ко-

ординат или имеет один полюс, то при стремлении

к беско-

ости

)( ω

∗

стремится либо к конечному

пределу (рис. 9.3). Таким обра

степень чис

и знаменате

нечн

альных линейных систем

сти

к нулю, либо

зом, характеристика ре-

всегда лежит в конечной -

)( ωj

плоско

∗

части

)(ω

∗

, в отличие от

(

)

, является четной функцией, поэтому

)( ω

∗

не будет симметричной относительно

вещ и.

венной о

Пусть вместо нелинейного элемента мы замыкаем систему ли-

сти-

характеристика

ест с

нейным элементом с характери

кой

kbbxy <<

, (9.10)

т.е. эта характеристика является част-

ным случаем р

нейных функций , поскольку

она располагается угловом секторе

∞

ассматриваемых нели-

()

xy Φ=

[

]

(рис. 9.2).

Совершенно ясно, что если исход-

ная нелинейная система удовлетворяет

условиям абсолютной

олученная линейная замкнутая система явл

Рис. 9.3. Модифицированная

амплитудно - фазовая

частотная характеристика

лине

йной части системы

устойчивости, то

п яется устойчивой.

187

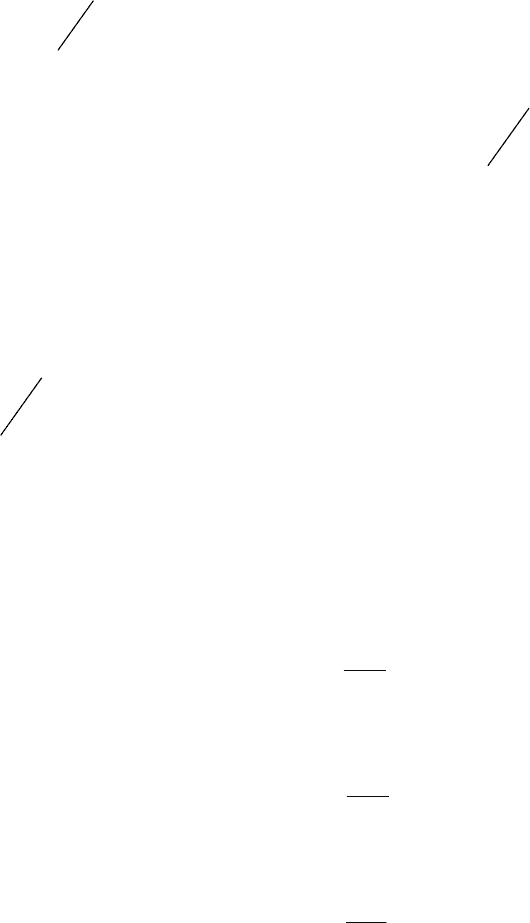
Частотные характеристики

)(

)( ω

∗

пересекают ве-

ществе одних и тех же точках. Дл

ной зам емы частотная характерист

нную ось в я устойчивой линей-

кнутой сист ика

)(

согласно критерию Найквиста, не должна пересекать отрезок

)

вещественной оси (или может п

Следовательно, характеристика

(

ересечь его четное число

1,−∞−

раз).

)(

не должна пересекать

(

)

отрезок

, −∞−

. Принимая во внимание интервал (9.10) изме-

нения b, следует утверждать, что

)( ω

коэффициента характеристика

не должна пересекать отрезок

⎟

⎠

⎞

⎜

∞− ,

⎝

⎛

−

(или должна

пересекать его четное число раз).

Можно доказать [13], чт для устойчивой линейн

системы как характеристика

о ой замкнутой

)(

, так и характеристика

∗

нигде не должны пересекать число

)( ωjW

резок

(даже четное раз) от-

⎟

⎠

⎞

⎜

⎝

⎛

− −∞

вещественной

9.2.2. ГЕОМЕТРИЧЕСКА

АБСОЛЮТНОЙ УСТОЙЧИВОСТИ

Первое неравенство в фо в

оси.

Я ИНТЕРПРЕТАЦИЯ КРИТЕРИЯ

ПОПОВА

рмуле (9.6) можно записать виде

() ()

0>+ωω−ω

hVU

(9.11)

или с учетом (9.9)

() ()

∗

() ()

>+ω−ω

∗

hVU

. (9.12)

Критический случай

=+ω−ω

∗∗

(9.13)

188

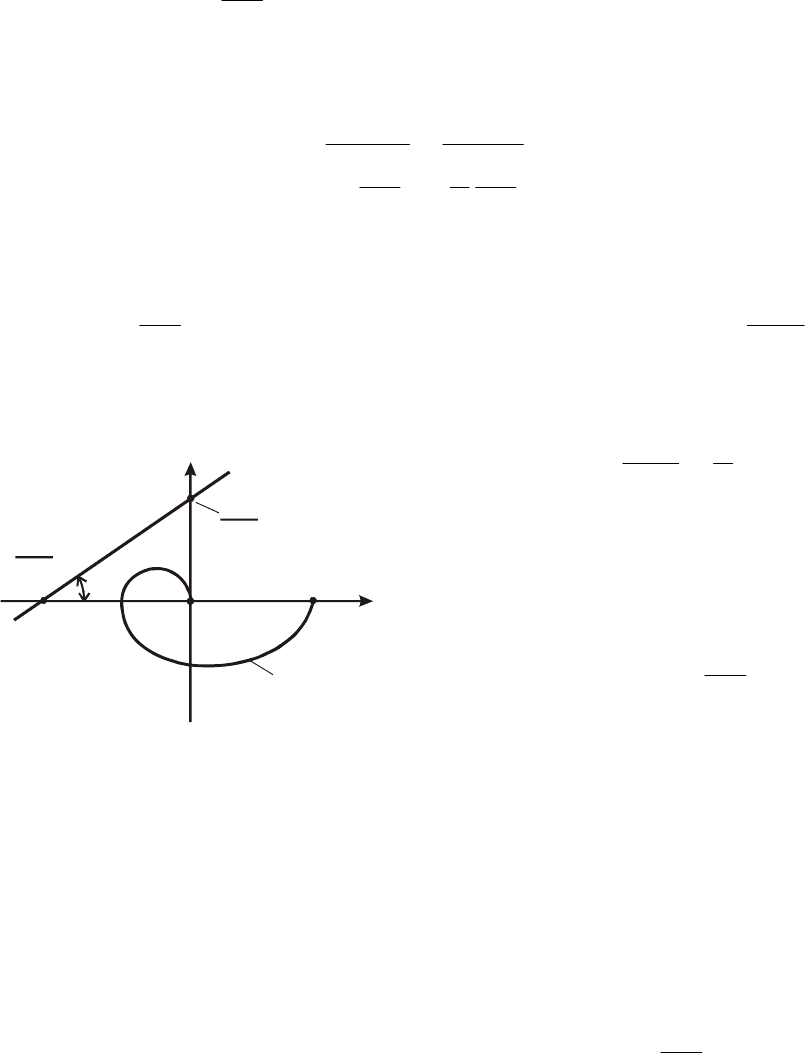
д в координатах ает

∗

уравнение прямой линии, которая в

точке

)( −=ω

∗

характеристикикасается

)( ω

∗

Уравнение прямой (9.13) в отрезках будет иметь вид

(

)

(

)

111

−

∗

. (9.14)

Уравнение (9.14) показывает, что прямая проходит через точ-

ку

−=

∗

вещественной оси и через точку

∗

мнимой

оси и имеет угловой коэффициент (рис. 9.4)

hhk

==α

. (9.15)

Эту прямую называют прямой Попо-

ва.

Когда

∗

ивая

−

∗

hVU

то кр

)( ω

∗

лежит правее пря-

мой. Отсюда вытекает следующая

критерия

Состояние равновесия нелинейной системы с

ционнным нелинейным элементом абсолютно устойчиво, если не-

геометрическая трактовка

Попова.

одним безынер-

линейная характеристика

)(

находится внутри углового сек-

тора и можно через точку

[]

α,0

провести

−

прямую Попова

ак, модифицированная частотная характер

нейной лежала от этой прямой справа,

т.е. в , начало координат.

т истика ли-чтобы

части

целиком

содержащей

)( ω

∗

плоскости

ная характ

∞

()

ис. 9.4. Прямая Попова и

модифицированная

частот еристика

инейной части системы

189