Зоценко Н.Л. Инженерная геология. Механика грунтов, основания и фундаменты

Подождите немного. Документ загружается.

220

жностей (9.37)-(9.40) для зони мінімального напруженого стану відповідно отримаємо:

−=

; (9.87)

−=

(9.88)

для зони максимального напруженого стану замість залежностей (9.46)-(9.49) одержимо:

−=

; (9.89)

−=

. (9.90)

Слід відзначити, що отримане вирішення вироджується у відоме для ізотропного ґру-

нту при незмінних за напрямками кутами внутрішнього тертя і зчеплення.

Несуча здатність анізотропного за опором зрушенню ґрунтового клину при сейс-

мічних діях довільної орієнтації на площині

Задача, що розглядається, є узагальненням результатів, отриманих раніше, на випадок

урахування сейсмічної дії, яке будемо проводити відповідно до статичної теорії, обґрунтова-

ної стосовно відповідних задач для ізотропного ґрунту у роботах Ш. Г. Напетрваридзе,

В. С. Христофорова, П. І. Яковлєва і широко використовуваної у практиці проектування гід-

ротехнічних споруд та їх основ. Таким чином, зберігаючи постановку задачі, розглянуту ра-

ніше, будемо вважати, що до масових сил, котрі діють на кожну із зон граничного напруже-

ного стану, додається відповідна складова

′

, зорієнтована під довільним кутом до горизон-

ту, значення якої згідно із загальноприйнятим підходом, реалізованим у нормативних доку-

ментах, визначається

⋅=

′

ici

, де α – добуток коефіцієнтів, зумовлених розрахунковою

сейсмічністю і функціональною відповідальністю споруди. При цьому результуюча масових

сил у кожній із зон зорієнтована до вертикалі під кутом ω (рис. 9.12), котрий можна визначи-

ти, виходячи з очевидної залежності:

ksin

kcos

arctg

−

. (9.91)

Для водонасиченого клину залежність (9.91) набуває вигляду

























−













ksinkcosarctg

αω

, (9.92)

де γ

та γ

– питома вага ґрунту відповідно у насиченому і виваженому стані.

Тоді при ρ та ρ

(у позначеннях попередньої задачі), які виражають за допомогою фо-

рмул відповідно

{ }

/]sin)ksin([arctg δσπβσαρ

+−−=

{ }

]cos)kcos()([/

δσπβσαβσ

+−−−

; (9.93)

{ }

/]sin)ksin([arctg δσπβασρ

′′

+−−

′

1111

{ }

]cos)kcos()([/

δσπβασβσ

′′

+−−

′

−

′

1111

, (9.94)

і згідно із залежностями (9.33)-(9.40), (9.42)-(9.49), (9.50)-(9.53) виконуємо вирішення кіне-

матичної частини задачі. При цьому зберігаються особливості вирішення, обумовлені анізот-

ропією й окремими випадками, що визначені залежностями (9.85)-(9.90). Статична частина

задачі отримає вирішення, аналогічне викладеному в попередній задачі. Однак при

з’ясуванні

– результуючих активних сил, зумовлених власною вагою і сейсміч-

ною дією, у кожній із зон у формулах (9.54)-(9.56) замість γ потрібно поставити γ

αγγ cos/)ksin(

−= 1

. (9.95)

У випадку водонасиченого ґрунту γ

становить

221

αγγ cos/ksin

вc













−= 1

. (9.96)

Кути орієнтації активних і реактивних сил відносно вертикальної осі визначаються за

формулами (9.64)–(9.79), виключаючи

, для яких

ωεεε

===

ccc

GGG

321

. Визна-

чення додаткових складових, зумовлених урахуванням годографа тиску зв’язності, не відріз-

няється від визначення за залежностями (9.59)–(9.62). Розглядаючи послідовно граничну рів-

новагу зон максимального напруженого стану, приходимо до залежностей, що визначають

несучу здатність

анізотропного за опором зрушенню ґрунту в загальному випадку водо-

насиченого зв’язного клину при сейсмічній дії, довільно орієнтованій відносно горизонталі.

У кінцевому вигляді послідовність для розрахунку

запишемо таким чином:

+++=

]cosQcosGcosQ[tg{VF

QcQ

33314

εωεε

}sinQsinGsinQ

QcQ

εωε

+++

, (9.97)

де

4341

−

)costg(sinV εεε

;

344333

εεεωε cos/]cosFcosQcosGcosQ[F

QcQ

−++=

; (9.98)

−++−=

]QcosGcosF[tg{VF

2233225

ωεε

ωε

2233

QsinGsinF

++−

, (9.99)

де

5252

−

−=

)costg(sinV εεε

;

22332552

εεωε cos/)QcosFcosGcosF(F

−+−=

; (9.100)

+−++−=

)cosFcosQcosQcosG(tg[VФ

Qcc

22441113

εεεωε

]sinQsinQsinGsinF

QQc

41122

εεωε

−+−+

, (9.101)

де

−

)tgcos(sinV

фф

εεε

Із виразів (9.97)–(9.101) виходить, що F

лінійно залежать від активних сил. У свою

чергу, активні сили, які визначають за виразами (9.54)–(9.56) з урахуванням виразів (9.95),

(9.96), лінійно залежать від добутку γb

, а сили, що визначають за формулами (9.59)–(9.63),

знаходяться у лінійній залежності від b, де b – ширина смуги завантаження. Звідси виходить,

φ(β

)

φ(β

)

φ(β′

)

φ(β′

)

G′

=αG

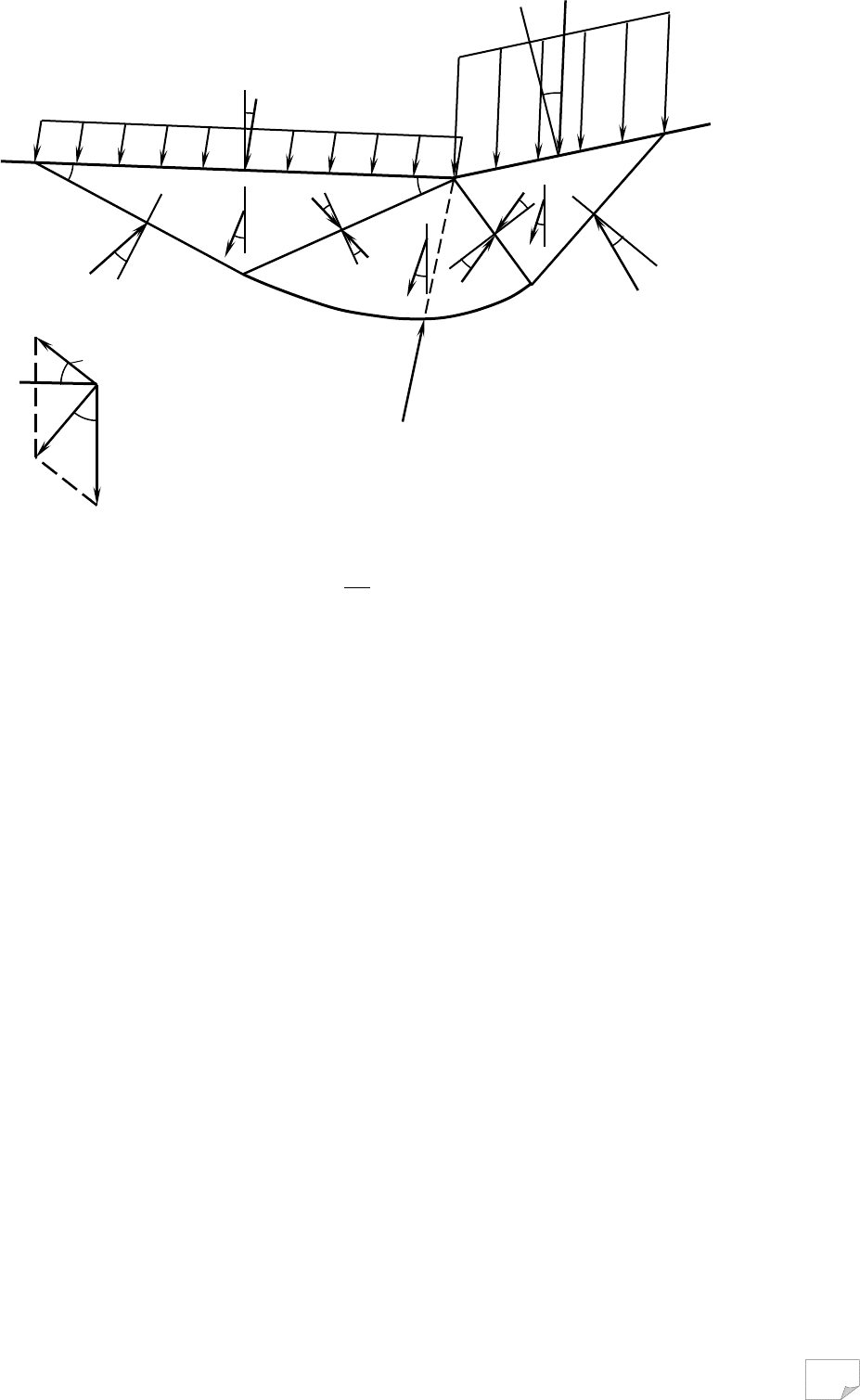
Рис. 9.12. Розрахункова схема визначення несучої здатності

анізотропного за опором зрушенню ґрунтового клину при сей-

смічній дії (а) і схема визначення ω ( б

); зображено позитивне

значення k

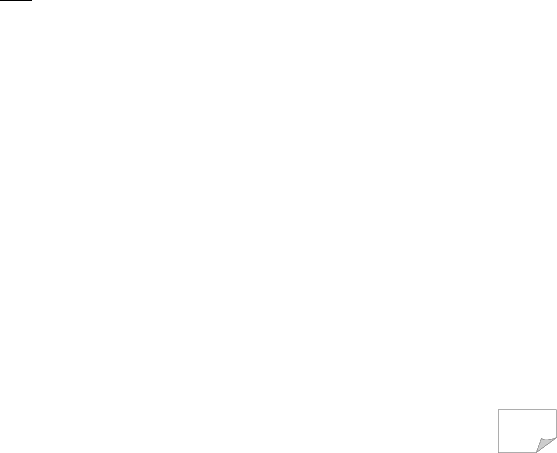
222

що реактивні зусилля (9.97)–(9.100) у загальному випадку можна записати у вигляді

i,c,qci

N)(bNbF

βσγ

, (9.102)

де

та

i,c,q

– безрозмірні коефіцієнти, перший із котрих фіксує вплив власної ваги і сей-

смічних дій на кожну з реакцій клину, а другий – вплив годографа зчеплення й приванта-

ження. Тоді несуча здатність Ф у підсумку може бути також представлена виразом

c,qcс

N)(bNb

βσγ

, (9.103)

де коефіцієнти

c,q

мають аналогічний зміст. Автором отримані вирази для

та

c,q

у кінцевому вигляді, але вони через громіздкість тут не наведені. Форма представлення

(9.103) є досить зручною для складання програми розрахунку на ЕОМ, а також для діагнос-

тичного аналізу основ портових споруд.

Несуча здатність анізотропних за опором зрушенню ґрунтових основ (анізотроп-

на напівплощина)

Практика аналізу несучої здатності основ причальних споруд ряду портів Чорномор-

сько-Азовського і Балтійського басейнів показує, що у переважній більшості випадків його

результати є визначальними при зміні завантаженості причалів або інших параметрів, які ха-

рактеризують експлуатаційний режим. Повною мірою несучу здатність основ слід віднести

до визначальних оцінок і на стадії проектних розроблень. У п. 9.2 відмічалось, що припу-

щення про ізотропію реального ґрунтового масиву є ідеалізацією, котра не завжди справед-

лива з причини різноманітності властивостей і умов утворення ґрунтів прибережної зони мо-

рів. У зв’язку з цим, урахування анізотропних властивостей ґрунтів під час оцінювання пове-

дінки основ портових споруд має практичний інтерес.

Результати, викладені раніше, дозволяють розв’язати поставлену задачу двома спосо-

бами: графоаналітичним й аналітичним. Сформулюємо постановку задачі. Дано ґрунтову на-

півплощину, опір зрушенню характеризується φ(β) с(β), які задовольняють вимоги (9.1),

(9.2). Осі відліку годографів збігаються із поверхнею ґрунту, яка є горизонтальною. По смузі

АВ (рис. 9.13) діє навантаження, результуюча якого відхилена від нормалі під довільним ку-

том δ. Відшукується несуча здатність.

Для побудови графоаналітичного розв’язання скористаємось результатами вирішення

задач у п. 9.2. Тоді кінематична частина задачі складається з наступних процедур:

згідно з алгоритмом графічних розв’язань основної задачі (п. 9.2) виконуємо побудову

трикутників, геометрично подібних зонам мінімального і максимального напруженого ста-

нів;

переносимо на масштабне креслення зону мінімального напруженого стану ABD, а та-

кож площадку ковзання зони максимального напруженого стану АЕ;

вимірявши на кресленні AD та кут розкриття проміжної зони

DAE

∠

, за допомогою

алгоритму, викладеного у п. 9.2, знаходимо

й напрям реакції F

, після чого завершуємо

побудову зони максимально напруженого стану AEK і проміжної зони;

на масштабному кресленні з’ясовуємо напрям реакції F

-F

, а також складових Q

та

графоаналітичним шляхом знаходимо відповідну вагу зон і значення Q

Статична частина задачі включає побудову векторної діаграми сил, у результаті чого

отримаємо в масштабі діаграми граничного опору основи.

Потрібно відмітити, що графоаналітичний спосіб розрахунку є достатньо трудоміст-

ким, оскільки ідентифікаційна частина задачі, яка тут для скорочення вилучена, потребує

попередньої побудови залежностей δ-δ

та β

-β

(див. рис. 9.7) і аналізу можливих варіантів

вирішення, серед котрих потрібно вибрати екстремальний. Крім того, цей спосіб не дає мож-

ливості автоматизувати розрахункові процедури за допомогою ЕОМ. Тому переваги слід

віддати аналітичному способові розрахунку.

По суті, задача, що розглядається, є окремим випадком більш загальної, розглянутої

на початку п. 9.2, яка вироджується в ту, що аналізується, при

πββ

′

. Тому можна ско-

223

ристатися раніше розглянутим алгоритмом для ґрунтового клину повною мірою. Зберігають

справедливість і залежності (9.32)–(9.90), в яких згідно з постановкою задачі, крім наведеної

рівності, необхідно також урахувати, що

)()(

βσβσ

′

та залежність (9.41) ρ

=0.

Аналогічним способом отримаємо вирішення при дії сейсмічних сил. У цьому випад-

ку алгоритм розрахунку використовують із відповідної задачі. За допомогою залежностей

(9.91)–(9.101), де ρ

=0, отримаємо необхідний результат.

Досить важливим для діагностики гідротехнічних споруд є врахування дії фільтрацій-

них сил в основі. П. І. Яковлєв розробив аналітичний метод розрахунку несучої здатності ос-

нови для ізотропного ґрунту. Визначена за цим методом фільтраційна сила Ф

, що діє на ко-

жну із зон граничного напруженого стану, зорієнтована під своїм кутом ω

до вертикалі. Як-

що прийняти припущення про ізотропність ґрунту за водопроникністю, отримаємо постанов-

ку задачі, яка принципово не відрізняється від задачі по врахуванню дії сейсмічного наван-

таження. Особливістю буде лише підрахунок результуючої масових сил G

іф

для кожної із зон

граничного напруженого стану і кутів їх орієнтації ω

відносно вертикалі. Тобто для вирі-

шення задачі можна скористатися залежностями (9.97)–(9.101) з поправками на окремий ви-

падок ґрунтового клина і підстановки замість G

іс

величин G

іф

і замість ω відповідних кожній

зоні значень ω

Таким чином, отриманий алгоритм містить достатньо широкий спектр діагностичних

задач для анізотропної за опором зрушенню основи, використовуючи при цьому єдину пос-

тановку, обумовлену теорією граничного напруженого стану, і відповідаючи фізичному

принципу відповідності, згідно з яким узагальнююча теорія повинна включати теорію, пере-

вірену практикою, як окремий випадок.

На рис. 9.13 наведено кінематичну схему руйнування основи для φ(β) та с(β) заданих

на рис. 4.23, при відсутності сейсмічних або фільтраційних сил. За розрахунками отримано,

що несуча здатність основи для ширини смуги завантаження b=10 м, γ=10 кН/м

і ρ=10°

складає Ф

ас

=21390 кН/м. При відсутності зчеплення, тобто при с(β)=0, несуча здатність

ас

=6342 кН/м. На рис. 9.14 показані поверхні ковзання, які одержані для максимального і

мінімального значень кутів внутрішнього тертя із заданого годографа. Для цих випадків не-

суча здатність ізотропної основи при відсутності зчеплення має відповідно такі значення:

)

(Ф

maxu

=8300 кН/м і

)(Ф

minu

=1250 кН/м. Можна побачити, що Ф

має для розглянутого

прикладу проміжне положення між

)

(Ф

maxu

та

)(Ф

minu

, що відповідає фізичній суті.

Аналогічний висновок не можна зробити відносно розвитку зон випору (див. рис. 9.14).

Для розглянутих у п. 9.3 окремих випадків залишається справедливою форма подання

несучої здатності основи у вигляді безрозмірних коефіцієнтів (вираз 9.103). Це дозволяє по-

δ=10°

Q=30 кН

Q=111 кН

Q=5 кН

Q=937 кН

Q≈0

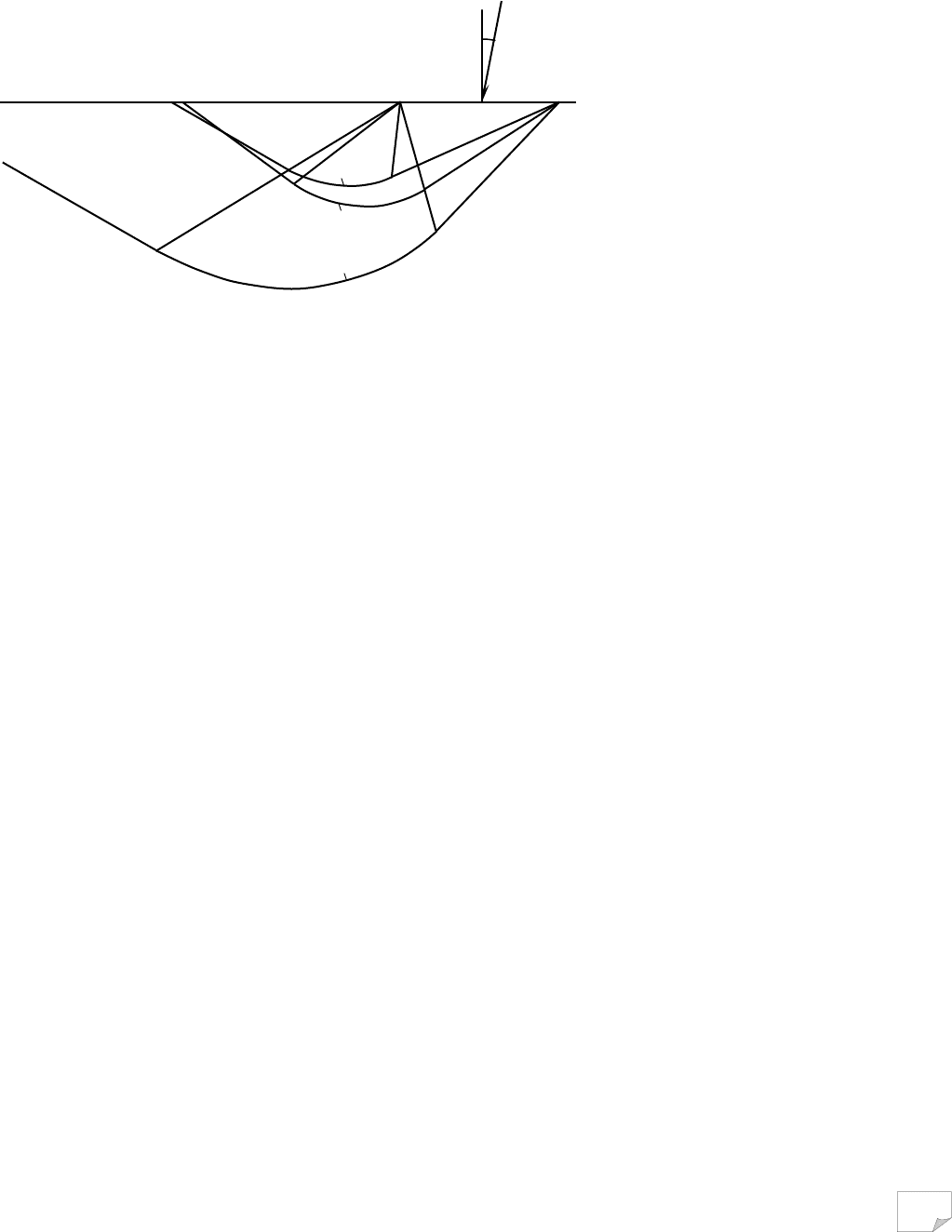
Рис. 9.13. Поверхні ковзання до прикладу розрахунку несучої здатності ані-

зотропної за опором зрушенню основи. Епюра відповідає залежності (8.177);

=5,44; N

q.c

=19,24

224

дати отримані результати у дещо іншому вигляді. Прийнявши за змінну b=x і продиферен-

ціювавши вираз (9.103) за нею, приходимо до епюри наведених напруг граничного опору ос-

нови

c,qcc.lim

N)(Nx

βσγσ

, (9.104)

яка лінійна за координатою x. На рис. 9.13 наведено епюру для розглянутого вище прикладу

розрахунку. Слід зазначити,

що при отриманні результа-

тів у вигляді залежності

(9.104) порушуються умови

рівноваги у зоні мінімально-

го напруженого стану.

Лінійний характер за-

лежності (9.104) зумовлений

припущенням про неваго-

мість основи, при розв’язанні

кінематичної частини задач,

розглянутих вище. Викладені

алгоритми цих задач припус-

кають уточнення на інтегра-

льне врахування власної ваги

кожної із зон граничного на-

пруженого стану шляхом по-

слідовних наближень.

Визначення бічного тиску анізотропного за опором зрушенню ґрунту на підпірні

стінки й огорожі

Активний тиск

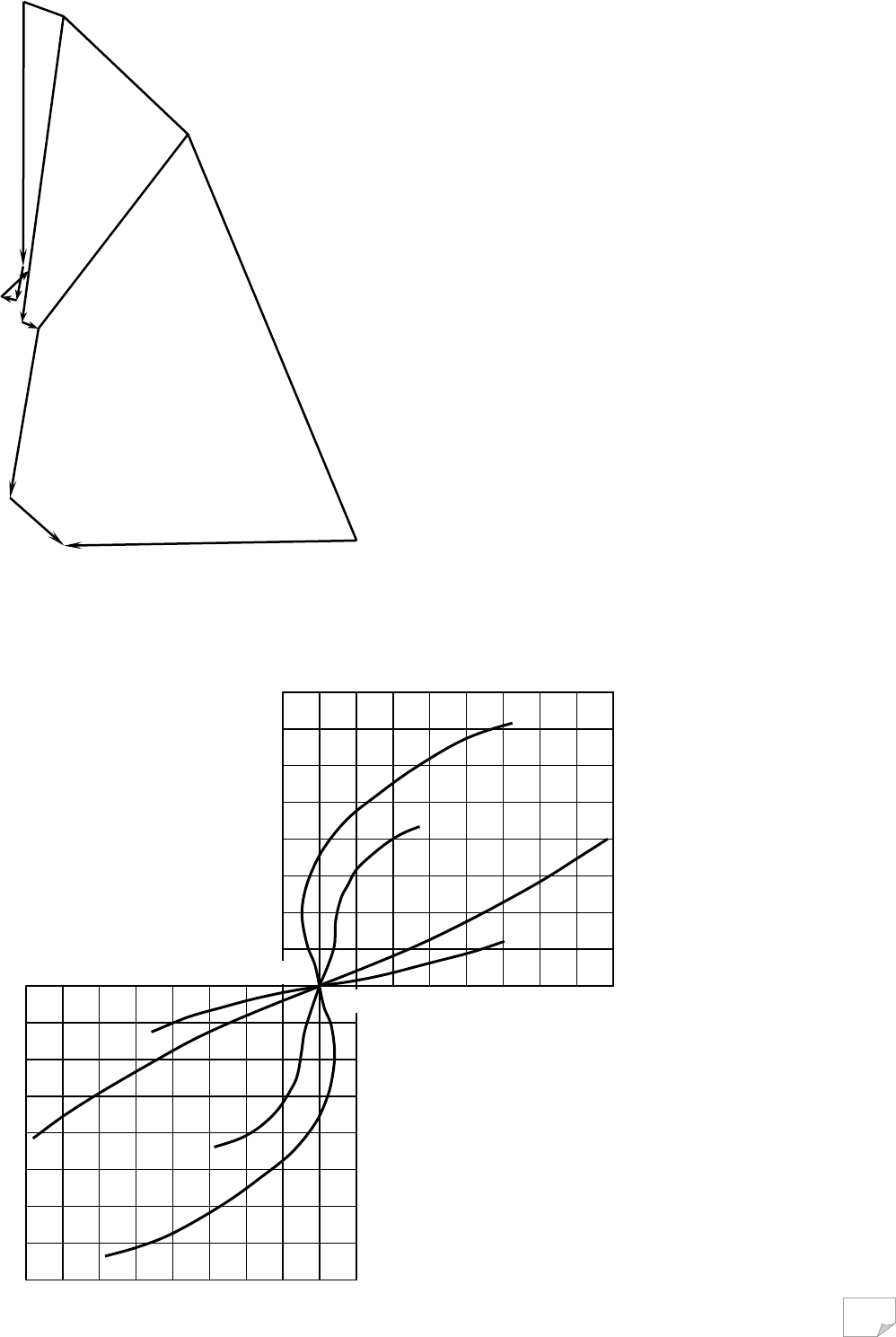
Сформулюємо постановку задачі. Розрахункова схема зображена на рис. 9.15. Ґрунто-

вий масив, поверхня якого зорієнтована під кутом β

до горизонталі, завантажений рівномір-

но розподіленим навантаженням інтенсивністю σ, що відхилена від нормалі під кутом

′

Підпірна стінка відхилена від вертикалі під кутом α, кут тертя ґрунту об стіну складає

′′

Анізотропні властивості ґрунту характеризуються годографами φ(β) та с(β), які задовольня-

ють умови (9.1), (9.2). На вигляд годографів обмежень не накладається.

Отримані у п. 9.2 результати дозволяють побудувати алгоритм графоаналітичного ви-

рішення задачі таким чином:

1. Визначаємо напрям результуючої Q наведених напруг, що діють на поверхні ґрун-

ту, згідно із залежностями

)]}(cos/[sin{arctg

βσδσδσρ

′′

, (9.105)

попередньо з’ясувавши з годографа тиски зв’язності σ

(β

). Оскільки величина результуючої

активного тиску невідома, знайшовши σ

(α), задаємось напрямком δ

наведеного активного

тиску.

2. Ідентифікаційну частину задачі для зон максимального і мінімального напруженого

стану вирішуємо за допомогою формул (9.14), (9.17) або згідно з графічною послідовністю

процедур, наведеною у п. 9.2, після побудови залежностей δ-δ

для обох зон з’ясовуємо мож-

ливі варіанти їх обрисів.

3. Кінематична частина задачі для кожного з варіантів реалізується за допомогою фо-

рмули (9.14) або графічної побудови для зони максимального напруженого стану, що прими-

кає до тилової грані огорожі.

4. За допомогою побудови, наведеної на рис. 9.7 (аналогічної для заданого годографа),

й залежності, аналогічної виразу (9.26), яка для розглянутої задачі запишеться у вигляді

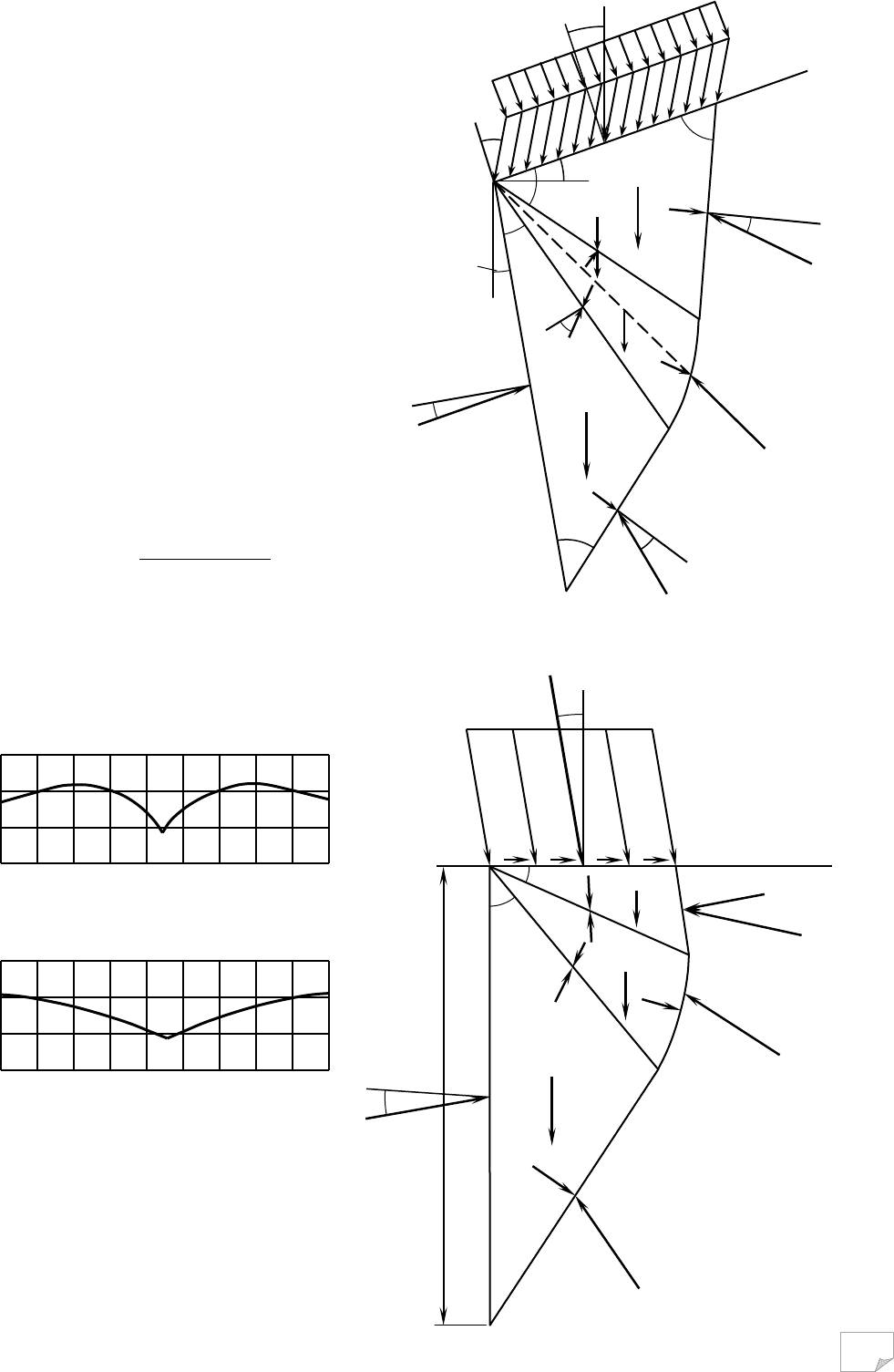
Рис. 9.14. Поверхні ковзання: 1 – для анізотропної за опором

зрушенню основи; 2 – для ізотропного при φ=φ

min

; 3 –

для

ізотропного при φ=φ

max

K′

D′

D″

E′

E″

=10°

225













∫

ββϕβ d)]([tgexpr)(r

, (9.106)

побудуємо загальну поверхню ковзання у

проміжній зоні і знайдемо значення r.

5. Вирішення кінематичної частини

задачі для фіксованого варіанта за-

вершується замикаючим зону мінімального

напруженого стану відрізком DB, напрям

якого визначається за формулою (9.14), або

графічним шляхом, котрий наведено у п. 9.2.

6. Статична частина задачі полягає у

побудові векторної діаграми сил, яка по суті

не відрізняється від аналогічної побудови,

поданої на рис. 9.11, але форма діаграми бу-

де дещо іншою. В результаті отримаємо

приведену результуючу активного тиску

а.пр

7. З’ясовуємо напрямок дійсного ак-

тивного тиску за допомогою графічної побу-

дови або залежності

TcosE

sinE

arctg

пр.а

−

′′

. (9.107)

8. Порівнюємо отримане відповідно

до залежності (9.107)

′′

із заданим у п. 1

40 160 0 80 120 β°

φ°

160

120

β°

, кПа

Рис. 9.16. До прикладу розрахунку

активного тиску анізотропного за

опором зрушенню ґрунту:

а – годограф тиску зв’

язності;

б – годограф кута внутрішнього те-

ртя; в – поверхні ковзання

=-10°

а.пр

ℓ=10 м

ρ=-10°

δ′

μ′

φ(β

)

φ(β′

)

а.пр

ν′

Рис. 9.15. Розрахункова схема для визначення

активного тиску анізотропного ґрунту

226

алгоритму, тобто відповідно

′′

та

′

. Якщо вони

не рівні, уточнюємо ρ і повторюємо розрахунок

згідно з пп. 2-7. Практика графічних розрахунків

показує, що задовільного збігу можна досягти на

другому або третьому наближеннях.

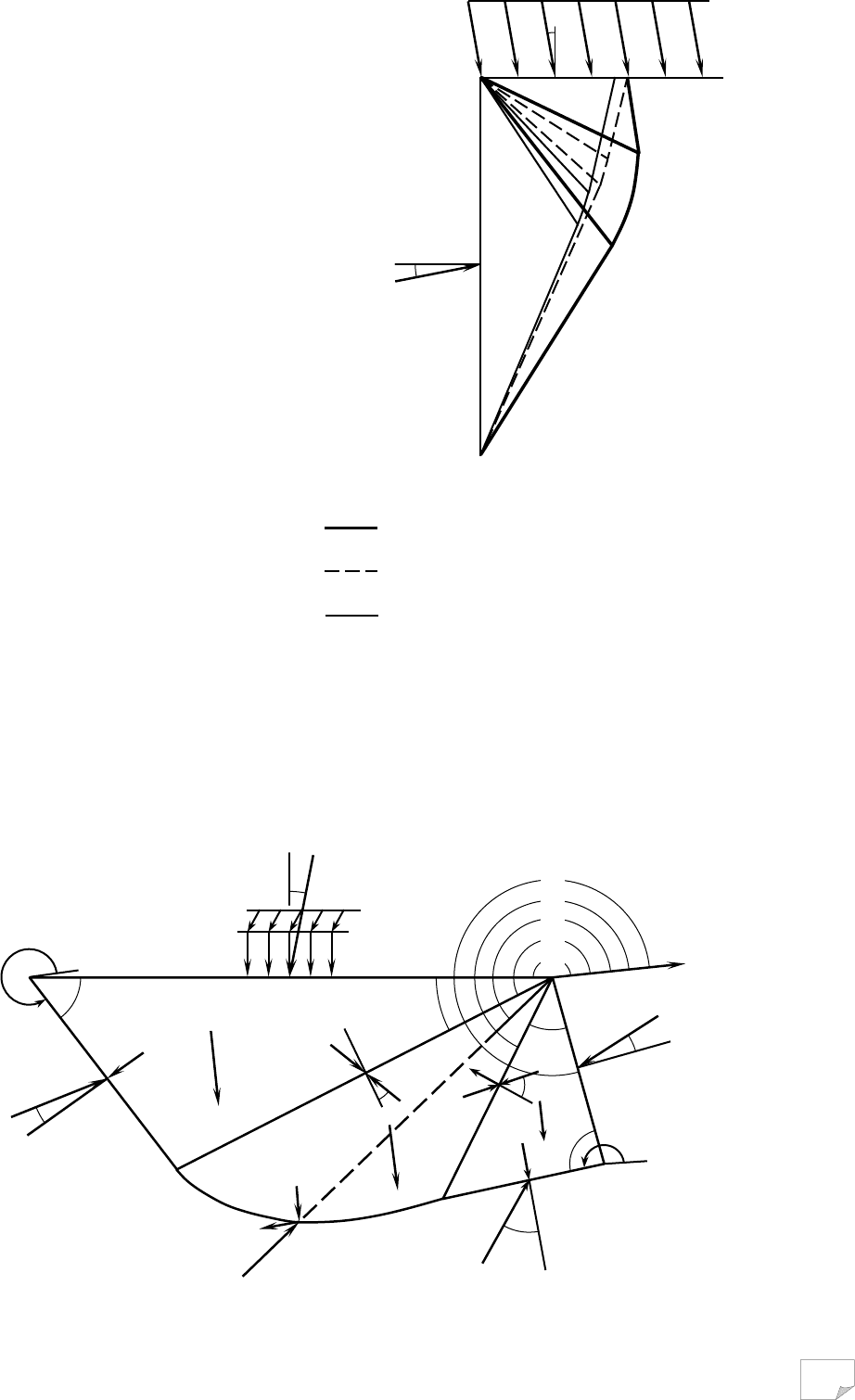
На рис. 9.16, 9.17 наведено результати роз-

рахунків, виконаних відповідно до викладеного

алгоритму і годографів, зображених на рис.

9.16, а. Вирішення отримано за допомогою залеж-

ностей, зображених на рис. 9.18. У якості вихідних

даних прийнято: γ=10 кН/м

, навантаження на по-

верхні засипки горизонтальне з інтенсивністю

q=12 кПа, тобто кут нахилу наведених напруг на

поверхні ґрунту ρ

=-10°, кут нахилу наведених на-

пруг на тиловій грані ρ=-10°. У результаті розра-

хунку одержано, що приведена результуюча акти-

вного тиску складає Е

а.пр

=312 кН/м.

На рис. 9.19 виконано зіставлення повер-

хонь ковзання, отриманих у розрахунку, з поверх-

нями ковзання для ізотропного ґрунту при іденти-

чних граничних умовах, але відповідних максима-

льному і мінімальному значенням кута внутріш-

нього тертя вихідного годографа (рис. 9.16, б).

Слід відзначити, що обрис поверхонь ковзання у

випадку ізотропного ґрунту досить істотно відріз-

няється від обрису поверхонь ковзання для анізот-

ропного ґрунту.

-4

-32

-28

-24

-20

-16

-12

-8

δ°

-32

-16

-12

-4

-20

-24

-28

-8

Рис. 9.18. До прикладів розрахунку бі-

чного тиску анізотропного за опором

зрушенню ґрунту: 1, 2 –

відносяться до

зони мінімального напруженого стану

відповідно площадкам β=180° і

β=270°;

3, 4 – побудовані для зони максималь-

ного напруженого стану відповідно

при β=180° і β=270°

а.пр

Рис. 9.17. Векторна діаграма сил до схе-

ми прикладу розрахунку активного тис-

ку анізотропного ґрунту, наведеної на

рис. 9.16

227

Алгоритм діагностики активного

тиску ґрунту, одержаний вище, легко

узагальнюється й у випадку сейсмічних

дій. Відмінність складається у визначен-

ні напрямку дії результуючої власної ва-

ги зон і складової сейсмічної дії (у рам-

ках статичної теорії урахування сейсмі-

ки). Для цього можна скористатися фор-

мулами (9.91) або (9.92).

Також необхідно з’ясувати γ

(у

позначеннях п. 9.3), яке розраховують за

допомогою формул (9.95) або (9.96). Як

правило, в інженерних розрахунках у

якості невигідного напрямку сейсмічної

складової вибирають горизонтальний,

але у загальному випадку це не завжди

справедливо з точки зору з’ясування екс-

тремального значення активного тиску.

Залежності (9.91), (9.92), а також (9.96)

не потребують цієї умови для розрахун-

ку.

Пасивний опір

Постановка задачі ідентична викладеній для активного тиску. Розрахункова схема зо-

бражена на рис. 9.20. Граничні умови на поверхні ґрунтового масиву з’ясовуємо за допомо-

гою формули (9.105). Наведений вище алгоритм графоаналітичного вирішення залишається

справедливим для випадку, котрий розглядається, якщо використовувати замість виразу

(9.106) формулу (9.26), отриману раніше.

Неважко побачити, що постановка задачі з діагностики пасивного опору анізотропно-

го ґрунтового масиву повторює раніше викладену в п. 9.3 для ґрунтового клину. Тому отри-

мані раніше аналітичні вирішення можуть бути використані стосовно до задачі, що розгляда-

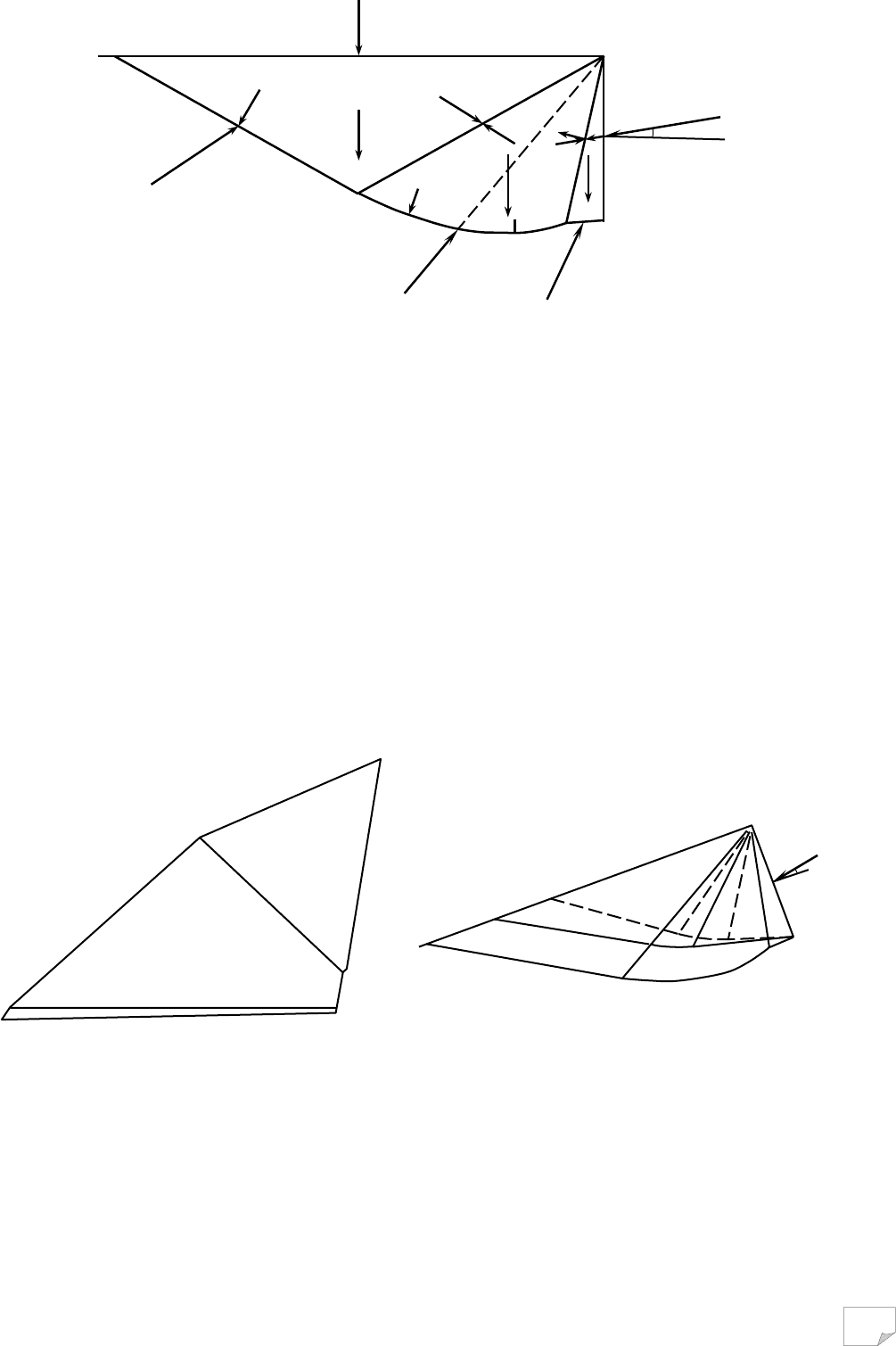
Рис. 9.20. Розрахункова схема визначення пасивного тиску анізотропного за

опором зрушенню ґрунту; наведені правила відліку кутів

β′

Вісь відліку

-ρ

п.пр

ℓ

φ(β

)

φ(β

)

φ(β′

)

φ(β′

)

10°

Рис. 9.19. Зіставлення поверхонь ковзання для

ґрунтів із такими характеристиками:

– анізотропний при годографі φ(β)

(рис. 8.26, б);

– ізотропний при φ, що дорівнює максим а-

льному значенню з вказаного годографа;

– те ж при φ=φ

min

228

ється. Спеціальним моментом є лише реалізація завершальних позицій розрахунку, які від-

повідають пп. 7 і 8 алгоритму для визначення активного тиску.

На рис. 9.21 та 9.22 наведені результати розрахунку для прикладу, вихідні дані котро-

го частково показані на рис. 9.21. Анізотропні властивості ґрунту характеризуються годог-

рафами, зображеними на рис. 9.16, а, б. Вирішення отримано за допомогою залежностей, по-

казаних на рис. 9.18. У якості вихідних даних для статичної частини задачі прийнято:

γ=10 кН/м

; ℓ=10 м.

Зіставлення поверхонь ковзання для анізотропного й ізотропного ґрунтів показує їх

суттєву відмінність (рис. 9.23) для розглянутого прикладу. Можна зробити висновок, що

врахування анізотропних властивостей ґрунтового масиву необхідне для аналізу роботи спо-

руд, які мають взаємодію з ґрунтом.

Можна також відзначити, що наведені результуючі активного і пасивного тисків при-

пускають форму представлення як функцію безрозмірних коефіцієнтів, аналогічну виразу

(9.103).

-ρ

п.пр

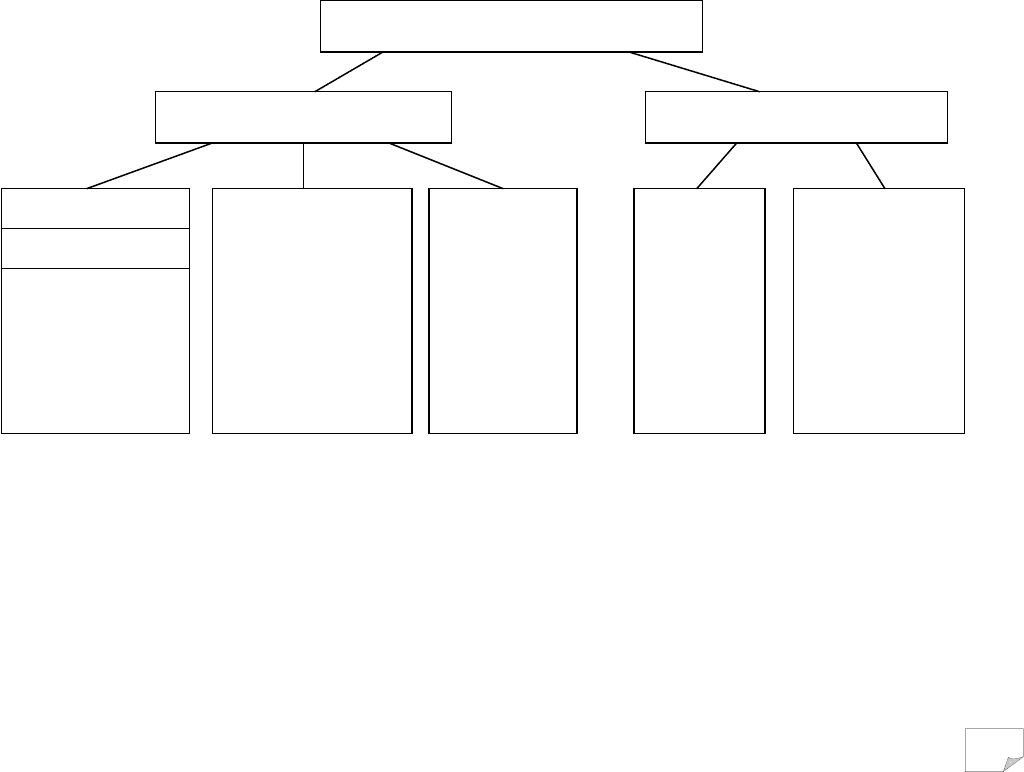
Рис. 9.21. Поверхні ковзання до прикладу розрахунку пасивного тиску

анізотропного за опором зрушенню ґрунту, властивості якого характери-

зуються годографами φ(β) і σ

(β), наведеними на рис. 8.26, а, б

п.пр

Рис. 9.22. Векторна діаграма сил до прикла-

ду розрахунку (схема на рис. 8.31); приведе-

на результуюча пасивного тиску Е

п.пр

=6900

кН/м. За відсутності зчеплення (σ

(β)=0

п.пр

=3270 кН/м. Для ізотропного ґрунту і

β=0 Е

п.пр

(φ

max

)=4100 кН/м

Рис. 9.23. Зіставлення поверхонь ковзання:

1 – анізотропний за опором зрушенню ґрунт;

2 – ізотропний при φ=31°, тобто φ= max[φ(β)];

3 – ізотропний при φ=18,5°, тобто φ=min[φ(β)]

п.пр

229

10. ЗАСТОСУВАННЯ ТЕОРІЇ НЕЛІНІЙНОГО

ДЕФОРМУВАННЯ ДЛЯ РОЗВ’ЯЗАННЯ

ЗАДАЧ МЕХАНІКИ ҐРУНТІВ

10.1. СУЧАСНІ УЯВЛЕННЯ ПРО НЕЛІНІЙНУ

ДЕФОРМАТИВНІСТЬ ҐРУНТІВ

Основи широкого кола споруд у складних інженерно-геологічних умовах (див. розділ

16), великомасштабних будівель із значними навантаженнями на несучі конструкції та фун-

даменти, об’єктів у аварійному й передаварійному стані тощо досить часто працюють за ме-

жею лінійного деформування. У ряді ж випадків і для досить традиційних рішень системи

“основа – фундаменти – будівля” величина її деформацій, одержана при застосуванні теорії

лінійного деформування (див. розділ 7), виявляється значно меншою за їх допустимі значен-

ня. Але запроектувати більші навантаження, згідно з положеннями лінійної механіки ґрунтів,

неможливо, адже при підвищенні навантаження порушується прийнята в розрахунках ліній-

на залежність між напругами й деформаціями.

На рис. 10.1 представлена структурна схема (за професором Д. М. Шапіро, 1996), яка

узагальнює основні види нелінійності, що зустрічаються при проектуванні будівельних

об’єктів, і яка охоплює більшість практично важливих задач та технічних теорій.

Фізична нелінійність матеріалів і ґрунтів проявляється як відхилення від закону Гука

співвідношень між деформаціями ε й діючими напругами σ. Це явище становить різні форми

розвитку пластичних деформацій: текучість – швидкоплинне деформування при постійних

напругах; повзучість – прогресування пластичних деформацій у часі; криволінійна діаграма

зв’язку між ε та σ, притаманна матеріалам (середовищам) із змінним (залежним від напруг)

модулем деформації чи із зміцненням, тобто здатністю сприймати зростаюче навантаження

при збільшенні пластичної складової деформацій. Нагадаємо, що характерна схема розвитку

деформацій ґрунтового масиву від дії на штамп (фундамент) зростаючого навантаження по-

дана на рис. 6.1, а типові графіки залежності ε=f(σ) найбільш поширених моделей ґрунту – на

рис. 6.11. Зазначимо також, що на порушення лінійної залежності між напругами і деформа-

ціями певною мірою впливають дилатансія та анізотропія ґрунтів, їх реологічні й динамічні

властивості (є сенс коротко переглянути п.п. 4.9-4.12).

Основні види нелінійності

фізична

геометрична

текучість

повзучість

криволінійна

діаграма

зв’язку між

напругами та

деформаціями

однобічні

зв’язки:

нездатність до

сприйняття

розтягнення

(стиснення)

зрушення

за заданою

(розрахун-

ковою)

поверхнею

поздовж-

ній

вигин,

втрата

стійкості

переміщення

в суцільних

тілах, сумірні

з розмірами

конструкцій

(кінцевих

елементів)

Рис. 10.1. Основні види нелінійності основ і будівельних конструкцій