Зоценко Н.Л. Инженерная геология. Механика грунтов, основания и фундаменты

Подождите немного. Документ загружается.

200

ні дуги ковзання з лінією дії ваги відсіку. Сили взаємодії вздовж вертикальних

площин відсіків не розглядаємо, тому що вважаємо їх однаковими за величи-

ною і протилежними за напрямом дії. Сили ваги відсіків розкладемо на складо-

ві, що діють у двох напрямах: уздовж радіуса обертання та перпендикулярно до

нього. Складемо рівняння рівноваги з урахуванням сил зчеплення, що діють уз-

довж усієї поверхні ковзання:

=−−

∑∑

cLRRtgNRT

, (8.37)

де L – довжина дуги ковзання; tgφ – коефіцієнт тертя; с – зчеплення ґрунту; T

та N

– складові від ваги відсіків, які визначають графічно або розраховують за

величиною кутів α

iii

sinPT α

;

iii

cosPN α

Скоротимо вираз (8.36) на R:

=−−

∑∑

cLtgNT

. (8.38)

За коефіцієнт стійкості укосу беруть відношення моменту утримуючих

сил ΣM

до моменту зсуваючих сил ΣM

∑













RcLtgN

, (8.39)

або

∑













cLtgN

. (8.40)

Розв’язання поставленої задачі не закінчується після визначення коефіці-

єнта стійкості для довільно вибраної дуги поверхні ковзання, тому що необхід-

но з усіх можливих дуг поверхонь ковзання вибрати найбільш небезпечну. Для

того щоб зменшити кількість спроб, розрахунки виконують у такій послідовно-

сті.

Із верхньої точки укосу В проводять похилу лінію під кутом 36° до гори-

зонту (рис. 8.7, б). На цій лінії розміщують точки O

, O

на відстанях,

показаних на рис. 8.7, б, де m=ctgα. Ці точки приймають за центри обертання.

Будують сліди круглоциліндричних поверхонь ковзання AC

, AC

для кожної поверхні розраховують значення коефіцієнта стійкості згідно з

формулою (8.39). Потім відкладають у деякому масштабі значення η

, η

вигляді відрізків, перпендикулярних до лінії BO

у відповідних точках. Через

кінці цих відрізків креслять плавну криву. До цієї кривої проводять дотичну,

паралельну лінії BO

, і точку дотику проектують на лінію BO

. Для одержаної

точки О роблять п’яте побудування й одержують мінімальне значення коефіці-

єнта стійкості, яке повинно бути не менше, ніж 1,1—1,3 залежно від класу спо-

руди.

Якщо в основі укосу залягають відносно слабкі ґрунти з кутом внутріш-

201

нього тертя менше від 10°, необхідно додатково розглянути можливість втрати

стійкості по круглоциліндричній поверхні А′С′, показаній штриховою лінією на

рис. 8.7, б, при випиранні ґрунту основи укосу.

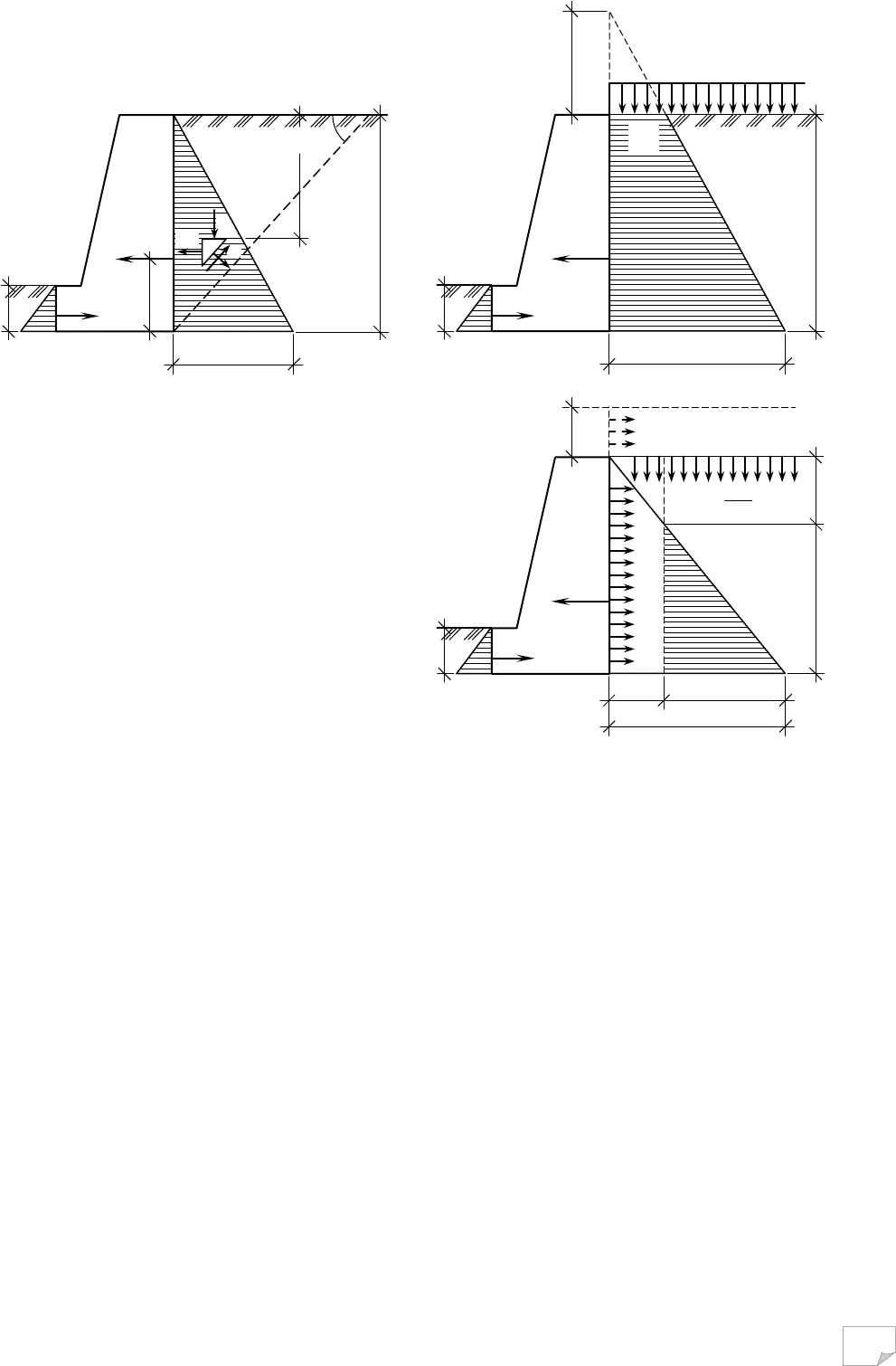
Стійкість притуленого укосу визначають, якщо можна прогнозувати мо-

жливий зсув мас ґрунту по ламаній поверхні ковзання (рис. 8.8). Сповзаючий

масив ґрунту розбивають вертикальними площинами на окремі відсіки і розг-

лядають сили, що діють на кожен із них, починаючи зверху вниз.

При розгляданні і-го відсіку враховують прикладене до нього зовнішнє

навантаження і силу ваги ґрунту відсіку, суму яких Q

розкладають у двох на-

прямах: перпендикулярно до площини зсуву цього відсіку вздовж основи та па-

ралельно до неї. Нормальна сила дозволяє врахувати сили тертя вздовж основи

. Крім того, враховують зчеплення ґрунту при зсуві по цій площині. Додат-

ково на відсік діють неврівноважений тиск від вищерозташованих відсіків E

i-1

та невідомий тиск на розміщені нижче відсіки E

. Розв’язання рівнянь рівноваги

(сум проекцій усіх сил на напрям A

і нормаль до нього) дає змогу знайти зна-

чення тиску E

, що передається на наступний відсік. Розрахунок починають із

першого відсіку, на який не діє зверху зсувний тиск, тобто E

i-1

=0. Потім, пере-

ходячи від відсіку до відсіку, досягають останнього відсіку n, що має бути стій-

ким при E

≤0, тобто сила E

повинна мати протилежний напрям.

Щоб укіс мав деякий запас стійкості, зсуваючі сили від власної ваги ґрун-

ту і зовнішніх навантажень збільшують на коефіцієнт запасу стійкості η.

8.6. ВИЗНАЧЕННЯ ТИСКУ ҐРУНТІВ НА ОГОРОЖІ

Якщо стійкість укосу не забезпечується, а зробити його більш пологим

неможливо, для його укріплення необхідно зводити підпірні стінки. Підпірні

стінки, які підтримують ґрунт, зазнають з його боку тиску, котрий має назву

активного. Якщо підпірна стінка сама передає тиск на ґрунт, то цей тиск буде

пасивним.

Визначення максимального тиску на підпірну стінку можна виконати ма-

тематично точно (якщо відомий точний обрис поверхні ковзання) або з деяким

і-1

i-1

i+1

Рис. 8.8. Схема для розрахунку

стійкості притуленого укосу

202

наближенням (при використанні припущення про плоску поверхню ковзання).

Найчастіше використовують припущення про прямолінійну поверхню

ковзання, запропоноване Ш. О. Кулоном, яке не дає значних похибок (2–3 %)

при визначенні активного тиску.

Це припущення формулюється так: поверхня ковзання має вигляд пло-

щини; з усіх можливих беруть ту поверхню ковзання, для якої тиск ґрунту на

підпірну стінку буде максимальним. Ґрунт вважається однорідним.

Максимальний тиск на підпірну стінку сипучих ґрунтів визначають так

(рис. 8.9, а). Будь-яка горизонтальна пло

щадка в ґрунті за масивною гладкою

вертикальною стінкою зазнає тільки стискуючої напруги (нормальної головної

напруги σ

), яка дорівнює вазі стовпа ґрунту від поверхні до площадки, що роз-

глядається:

⋅=

zγσ

, (8.41)

де z – відстань від горизонтальної поверхні ґрунту до площадки, котра розгля-

дається.

Бічний тиск ґрунту визначимо з умови, що ґрунт за підпірною стінкою

знаходиться в стані граничної рівноваги

)/(

tg/

245

ϕσσ

−°=

. (8.42)

Беручи до уваги вираз (8.40), одержимо

45°+φ/2

2max

H/3

2φ

Рис. 8.9. Схеми для визначення

тиску на підпірну стінку:

а – ідеально сипучого ґрунту;

б – ідеально сипучого ґрунту з

урахуванням додаткового наван-

таження; в – зв’язного ґрунту

2max

′

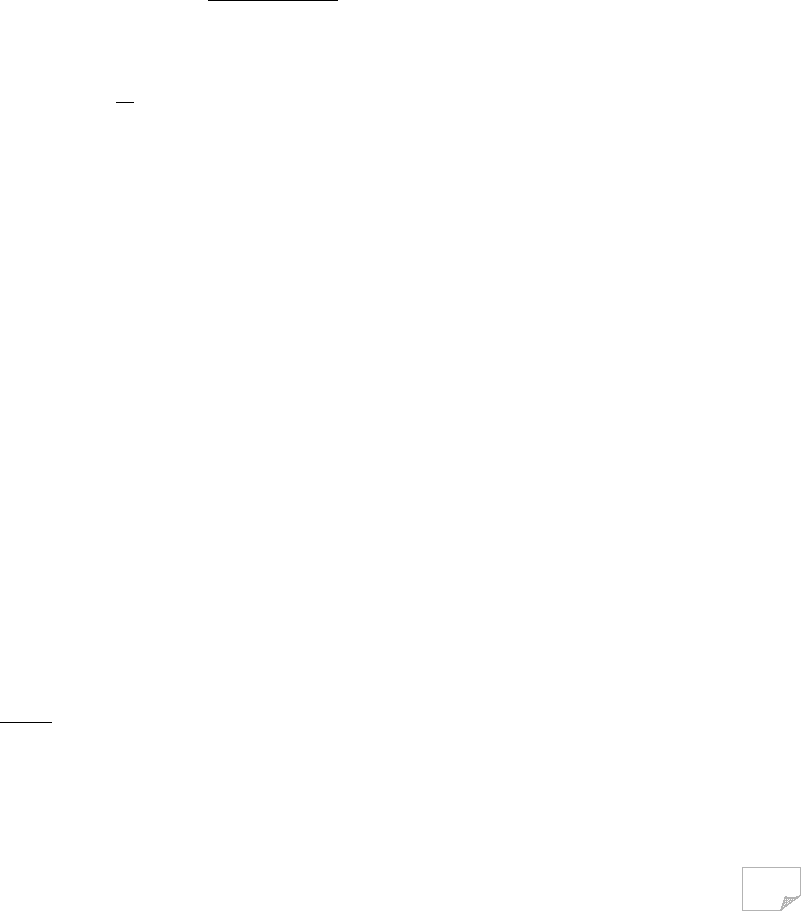
203

)/(ztg

245

ϕγσ

−°=

. (8.43)

Епюра тиску ґрунту має вигляд трикутника.

З другого боку підпірної стінки буде діяти пасивний тиск σ

)/(tgH

245

ϕγσ

+°=

. (8.44),

Рівнодіюча активного тиску ґрунту на підпірну стінку дорівнює площі

епюри тиску (рис. 8.9, а):

/HE

maxa

, (8.45)

)/(tg)/H(E

2452

ϕγ

−°=

. (8.46)

Рівнодіюча E

має горизонтальний напрям і прикладена на відстані однієї

третини висоти від низу підпірної стінки.

У випадку дії на поверхню ґрунту суцільного, рівномірно розподіленого

додаткового навантаження q (рис. 8.9, б) визначаємо приведену висоту шару

ґрунту h=q/γ, що заміняє його дію, продовжуємо задню грань стінки до перети-

ну з новою лінією засипки і будуємо загальну трикутну епюру тиску. На підпі-

рну стінку буде діяти тільки частина епюри, що має вигляд трапеції. Рівнодіюча

активного тиску

max

σσ

′

, (8.47)

або

)/(tg)HhH(E

2452

−°+=

. (8.48)

Для визначення тиску зв’язних ґрунтів на підпірну стінку замінимо дію

сил зчеплення всебічним рівномірним тиском зв’язності (рис. 8.9, в). Це дає

можливість використати умови граничної рівноваги для сипучих ґрунтів. При-

ведемо дію тиску зв’язності до еквівалентного шару ґрунту і, враховуючи про-

тилежність дії тиску P

у горизонтальному напрямі так само, як і для сипучих

ґрунтів, одержимо

ϕγσ p)/

(tg

)hH(

−−°+= 245

. (8.49)

Ураховуючи, що h=c/γtgφ і p

=c·ctgφ, після нескладних перетворень

одержимо

)/(tgc)/

(tgH

2452245

ϕϕγσ

−°⋅⋅−

−°⋅⋅=

. (8.50)

Із виразу (8.49) видно, що зчеплення ґрунту зменшує тиск ґрунту на під-

пірну стінку на величину 2·c·tg(45°-φ/2). За умови σ

=0 знайдемо h

. Тиск

зв’язних ґрунтів на підпірну стінку буде дорівнювати площі трикутника зі сто-

ронами σ

та H-h

/)hH(E

−=

. (8.51)

Підставивши відповідні значення σ

та H-h

, одержимо

γϕϕ

/c)/(cHtg)/(tg

22452245

+−°−−°=

. (8.52)

У деяких випадках визначити тиск ґрунту на підпірну стінку аналітичним

методом дуже складно. Тоді можна використати графічний метод, запропоно-

ваний Ш. О. Кулоном, який оснований на таких двох припущеннях:

204

поверхня ковзання має плоский вигляд;

призма обвалення відповідає максимальному тискові ґрунту на підпірну

стінку, тому для розрахунку необхідно знайти таку поверхню ковзання, яка бу-

де відповідати максимально можливому тискові на стінку.

Крім того, вважають, що призма обвалення є твердим тілом, що дозволяє

використати рівняння рівноваги для неї як для суцільного тіла.

Побудування Кулона виконується в такій послідовності. Через нижню то-

чку А задньої грані підпірної стінки проводимо можливу поверхню ковзання АС

під кутом α до горизонту (рис. 8.10). Потім знаходимо сили, що діють на

призму обвалення. Нехай вага призми ґрунту АВС з урахуванням можливих зо-

внішніх навантажень у межах призми обвалення дорівнює Q. Ця сила вертика-

льна. Внаслідок тиску призми обвалення виникає реактивна сила Е. Вона утво-

рює з нормаллю до задньої поверхні стінки кут тертя ґрунту об стінку φ

, який

складає частину кута внутрішнього тертя ґрунту φ. Звичайно для глин прийма-

ють φ

=0. Для сипучих ґрунтів φ

=0,67φ. Третьою силою, що діє на призму

АВС, є реакція R нерухомого масиву ґрунту. Ця реакція відхилена від нормалі

до площини АС на кут внутрішнього тертя φ. Силу Q легко визначити, розгля-

даючи рівновагу ділянки підпірної стінки довжиною 1 м

∑

+⋅=

qABCAQ γ∆

, (8.53)

де Σq – сума всіх зовнішніх вертикальних навантажень, що діють у межах по-

верхні ВС.

Знаючи силу Q і напрями дії сил Е та R, можна побудувати силовий три-

кутник FGH (рис. 8.10), тому що призма обвалення перебуває у граничному

стані. Для побудови такого трикутника відкладаємо в масштабі силу Q, потім

під кутом α-φ креслимо з точки F напрям реакції R, а з точки G під кутом ψ –

напрям сили Е. Точка перетину Н дає змогу знайти значення сили E в масштабі,

в якому була побудована сила Q.

Для того щоб визначити максимально можливий тиск на підпірну стінку

АВ, виконують кілька побудувань, задаючись можливими поверхнями ковзання

...AC

(рис. 8.10). Для цих поверхонь виконують розрахунки і побудування

так само, як і в першому випадку для поверхні АС. Остаточно для розрахунку

α-φ

Рис. 8.10. Графічне визначення тиску на підпірну стінку

α-φ

205

стійкості підпірної стінки приймають найбільше з одержаних значень сили Е.

9. ГРАНИЧНИЙ НАПРУЖЕНИЙ СТАН

АНІЗОТРОПНИХ ОСНОВ

9.1. УМОВИ ГРАНИЧНОГО НАПРУЖЕНОГО СТАНУ

АНІЗОТРОПНОГО ЗА ОПОРОМ ЗРУШЕННЮ ҐРУНТУ

І РОЗРАХУНКОВА МОДЕЛЬ

Загальні питання, пов’язані з анізотропією ґрунтів, були детально розглянуті раніше у

п. 4.10. Нижче розглядаються основи теорії граничного напруженого стану анізотропних за

опором зрушення ґрунтів.

Під характеристикою анізотропії зрушення будемо розуміти функцію τ(β, x, y) грани-

чного опору зрушенню по елементарній площадці, зорієнтованій під кутом β у довільній т о-

чці x, y, що належить ґрунтовій напівплощині. Тоді зручною формою представлення τ(β, x, y)

є годографи кута внутрішнього тертя φ(β, x, y) і питомого зчеплення с(β, x, y). Під однорід-

ною анізотропною напівплощиною будемо розуміти напівплощину, яка задовольняє умови:

φ(β,x,y)=φ(β); с(β,x,y)=с(β). (9.1)

Для реальних ґрунтових умов наслідком умови (9.1) є також відповідність залежнос-

тям:

φ(β)=φ(π+β); с(β)=с(π+β). (9.2)

У випадку регулярної площинно-паралельної шаруватості, крім задоволення умов

(9.1), (9.2), годографи φ(β) та с(β) як мінімум мають дві ортогональні осі симетрії.

Розглянемо елементарну площадку АВ, що проходить через довільну точку x, y, що

належить ґрунтовій напівплощині, анізотропні властивості якої відповідають умовам (9.1),

(9.2) і яка зорієнтована під кутом β до вибраної осі відліку. Показники анізотропії за опором

ґрунту зрушенню зафіксовані за допомогою φ(β) і с(β). Тоді умову граничного напруженого

стану в головних напругах за аналогією з ізотропним ґрунтом запишемо у вигляді

)](sin[)( βϕσσσσ

2121

+=−

, (9.3)

де

)

(

βσσσ

)

(

βσσσ

– приведені головні напруги,

)]

([ctg)(c)(

βϕββσ

– тиск зв’язності.

Повернемо площадку АВ на кут β. Для ізотропного ґрунту ця операція не приведе до

необхідності зміни відношення

)

/()(

2121

σσσσ

+−

в умові (9.3). Тобто у цьому

випадку, скориставшись поняттям про орієнтова-

ний круг Кулона-Мора, головний діаметр якого

суміщений із нормаллю до площадки АВ, при

обертанні останньої прийдемо до відомої системи

характеристичних кругів (рис. 9.1), котра є графі-

чним аналогом умови (9.3) для ізотропного ґрун-

ту при повороті площадки АВ. Для анізотропного

ґрунту виконання умови (9.3) при повороті пло-

щадки потребує іншого напруженого стану, тому

умова граничного напруженого стану не буде ін-

варіантністю відносно β. Побудова графічного

аналога умови (9.3) можлива, якщо виходити з

наступного. Неважко побачити, що ліва частина

умови у записі (9.3)

=−=−

2121

σσσσ

не за-

лежить від характеристик середовища, тому для

Рис. 9.1. Графічний аналог умови (9.56)

для ізотропного ґрунту при

обертанні

площадки АВ: 1-3 –

характеристичні

площадки

(х, у)

d/2

206

зручності подальших побудов доцільно зафіксувати d. Як і раніше будемо використовувати

орієнтований круг Кулона-Мора. Тоді при обертанні площадки АВ (рис. 9.2, б) точка О

буде

описувати огинаючу характеристичного круга площадок. На рис. 9.2, б наведений результат

цієї побудови для φ(β), що зображений на цьому ж рисунку. Розрахунок R

та R

, які необхід-

ні для побудови, виходячи з рис. 9.2, б, можна виконати за допомогою елементарних залеж-

ностей

)]b(sin[d,)/(R)(R ϕπβα

⋅=+= 502

;

)]b(sin[/d,)/(R)(R ϕπβα

502

=+=

Отримана система фігур є графічним аналогом умови (9.3) для анізотропного ґрунту.

Для того, щоб ним скористатися при довільному куті β

орієнтації площадки АВ, необхідно

виконати побудову у такій послідовності:

з центру О провести лінію ОО

під кутом α=β+π/2 відносно осі відліку до перетину з

огинаючою кута полюсів;

у точці О

провести хорду аb перпендикулярно до лінії ОО

, яка буде паралельною за-

даній площадці АВ;

завершують побудову дотичні О

a та О

b, які показують граничний кут відхилення

наведеної напруги по АВ.

Круг радіусом d/2, що називають кругом вершин, є геометричною подобою гранично-

го круга Кулона-Мора. У цьому можна впевнитись, виходячи із залежності (9.4).

Можна також запропонувати інші форми графічного аналога умови (9.3), але наведе-

ний є найбільш зручним для подальшого аналізу. Відзначимо також, що при φ(β)=const R

(α)

та R

(α) перетворюються у постійні величини. Отже, розглянута система фігур вироджується

у систему характеристичних кругів для ізотропного ґрунту, чого і варто було чекати.

Приклад побудови графічного аналога умови (9.3). Основа задовольняє умови (9.1),

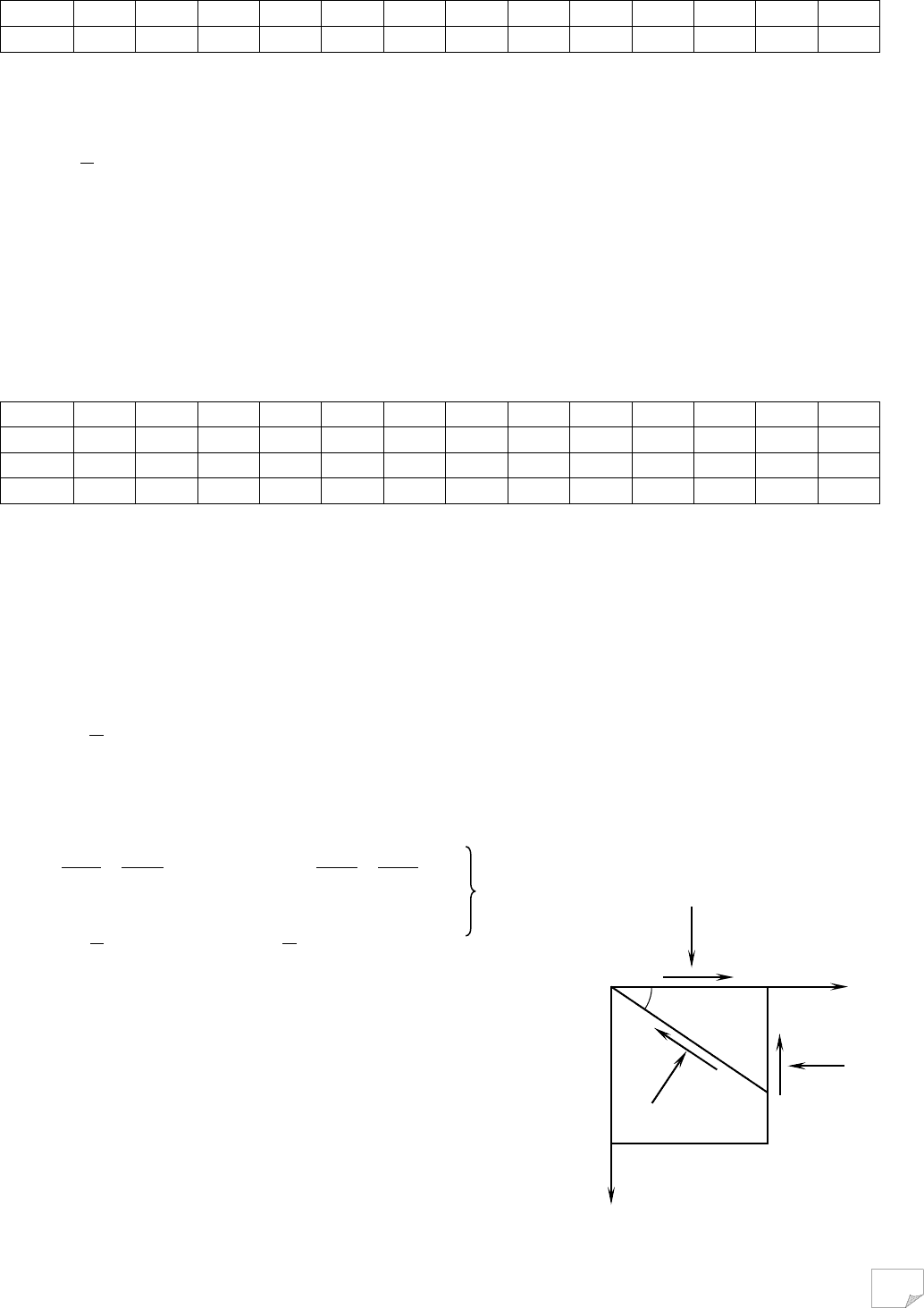
(9.2). Напрямок осі відліку кутів β – горизонтальний. Годограф φ(β) (рис. 9.2, а) заданий зна-

ченнями, що наведені у табл. 9.1.

(9.4)

Рис. 9.2. До прикладу побудови графічного аналога умови (9.56):

а –

вихідний годограф кута внутрішнього тертя (див. табл. 9.1);

б – згідно з результатами розрахунку (див. табл. 9.2)

180°

195°

210°

225°

240°

255°

270°

150°

120°

135°

165°

75°

90°

105°

60°

45°

30°

15°

φ°=15, 20, 25, 30,

φ(β)

α=0°, β=0°

(α)

d/2

207

Таблиця 9.1. Вихідні дані для побудови годографа

β°

105

120

135

150

165

180

φ°(β)

Розраховуємо коефіцієнт анізотропії μ

max

/πρΩµ

−=

, (9.5)

де

∫

ββρΩ

d)(

, а ρ(β) – функція φ(β).

Для прийнятої залежності φ(β) розраховане за виразом (9.5) значення μ

=0,398, що пі-

дтверджує дані про суттєву анізотропію основи.

Приймаємо d=5 (масштаб побудови може бути довільним). Для кожного β із наведе-

них у табл. 9.1 визначаємо R

(α) та R

(α). З умови (9.2) видно, що R

(α+π)=R

(α) й

(α+π)=R

(α). Це дозволяє скоротити обчислення вдвічі. Результати обчислень наведені у

табл. 9.2.

Таблиця 9.2. Результати обчислень для побудови рис. 9.2

β°

105

120

135

150

165

180

α°

105

120

135

150

165

180

195

210

225

240

255

270

(α)

0,9

1,3

1,2

1,0

0,9

0,7

0,64

0,6

0,64

0,7

0,9

(α)

7,3

4,7

5,0

6,1

7,3

8,5

9,65

10,4

9,65

8,5

7,3

За результатами розрахунків виконуємо побудову (див. рис. 9.2, б). Варто відмітити,

що при формулюванні умови граничного напруженого стану у вигляді (9.3) неявним чином

використана теорема А. Како відносно врахування зчеплення в основі. Ця ж обставина дала

можливість без особливих ускладнень побудувати графічний аналог умови (9.3) для анізот-

ропної напівплощини.

Окрім умови граничного напруженого стану у вигляді (9.3), у подальшому будемо ви-

користовувати також його іншу форму

)]([tg)( βϕσβ

, (9.6)

де

)(

βσσσ

ββ

– наведена нормальна напруга на площадці ковзання.

Розрахункова модель невагомої ґрунтової напівплощини в теорії граничного напру-

женого стану, як відомо, містить два рівняння рівноваги у нескінченно малих і умову (9.3),

відображену у компонентах напруг:

∂

;

∂

yxy

στ

;

)]

([sin)()(

yxxyyx

βϕσστσσ

2222

4 +=+−

де

)

(

cxx

βσσσ

та

)(

cyy

βσσσ

– наведені компо-

ненти напруг.

Скористатись рівнянням (9.7) у практичних розраху-

нках, як правило, дуже складно. Розглянемо дещо іншщий

підхід до побудови рівнянь рівноваги, що входять у систему

(9.7). Нехай напружений стан у точці заданий компонента-

ми напруг. Навкруги точки побудуємо елементарний пря-

мокутник (рис. 9.3); через точку А проведемо площадку АВ,

яка зорієнтована відносно осі y під кутом β, і будемо вважа-

ти АВ площадкою ковзання. Для зручності також будемо

вважати довжину АВ одиничною. Тоді з умови рівноваги

ABD отримаємо три рівняння:

(9.7)

cosβ

sinβ

Рис. 9.3. До аналізу ро-

зрахункової моделі

208

βσβσβτσ

cossinsin

xyxy

−−=

; (9.8)

βτβσστ

cossin)

(

xyxy

−−=

; (9.9)

022

=+−+

βσβσβσβ

ββ

sincoscossin

. (9.10)

Підставляючи вирази (9.8), (9.9) у рівняння (9.10), у підсумку отримаємо співвідно-

шення

βσσσσβ

cos)(sin

yxyxxy

+−=+−

, (9.11)

яке разом з умовою граничного стану, записаного у рівняннях (9.7), при заданих компонен-

тах напруг у точці шляхом послідовних наближень дозволяє знайти напрямок дотичної до

кривої ковзання у даній точці. Одержана система рівнянь у дійсних компонентах напруг має

такий вигляд:

ββσσσσσβτ

222

cos)]([sin

cyxyxxy

++−=+=

;

)]

([sin)]([)

(

cyxxyyx

βϕβσσστσσ

2222

24 +−=+−

Якщо у системі (9.12) прийняти

σσσσ

=>=

, то

, і в результаті отримає-

мо

βσσσσσ

2121

cos]с)([

++=−

;

)](sin[]с)([

βϕβσσσσσ

2121

++=−

або в підсумку

/)(/ βϕπβ

=±

. Знаки перед β показують, що реалізуються дві симет-

ричні площадки ковзання. Однак це справедливо лише у тому випадку, коли годографи φ(β)

та с(β) мають дві ортогональні осі симетрії, одна з яких збігається з напрямом σ

або σ

. У

протилежному випадку друга площадка, як і перша, відшукується послідовним наближенням

та дотична до поверхні ковзання недзеркальна відносно осі y. Таким чином, використання

системи (9.12) також приводить до громіздких розрахунків при визначенні кінематичної кар-

тини руйнування анізотропної основи.

9.2. ВИРІШЕННЯ ЗАДАЧ ДЛЯ АНІЗОТРОПНОЇ

ЗА ОПОРОМ ЗРУШЕННЮ ОСНОВИ

Основна задача

Основною вважають задачу відшукування напрямів характеристик через кінці заданої

елементарної площадки, завантаженої наведеною напругою, відхиленою від нормалі до пло-

щадки під довільним кутом δ. При вирішенні цієї задачі будемо оперувати анізотропною на-

півплощиною із заданими φ(β) та с(β), які відповідають умовам (9.1), (9.2).

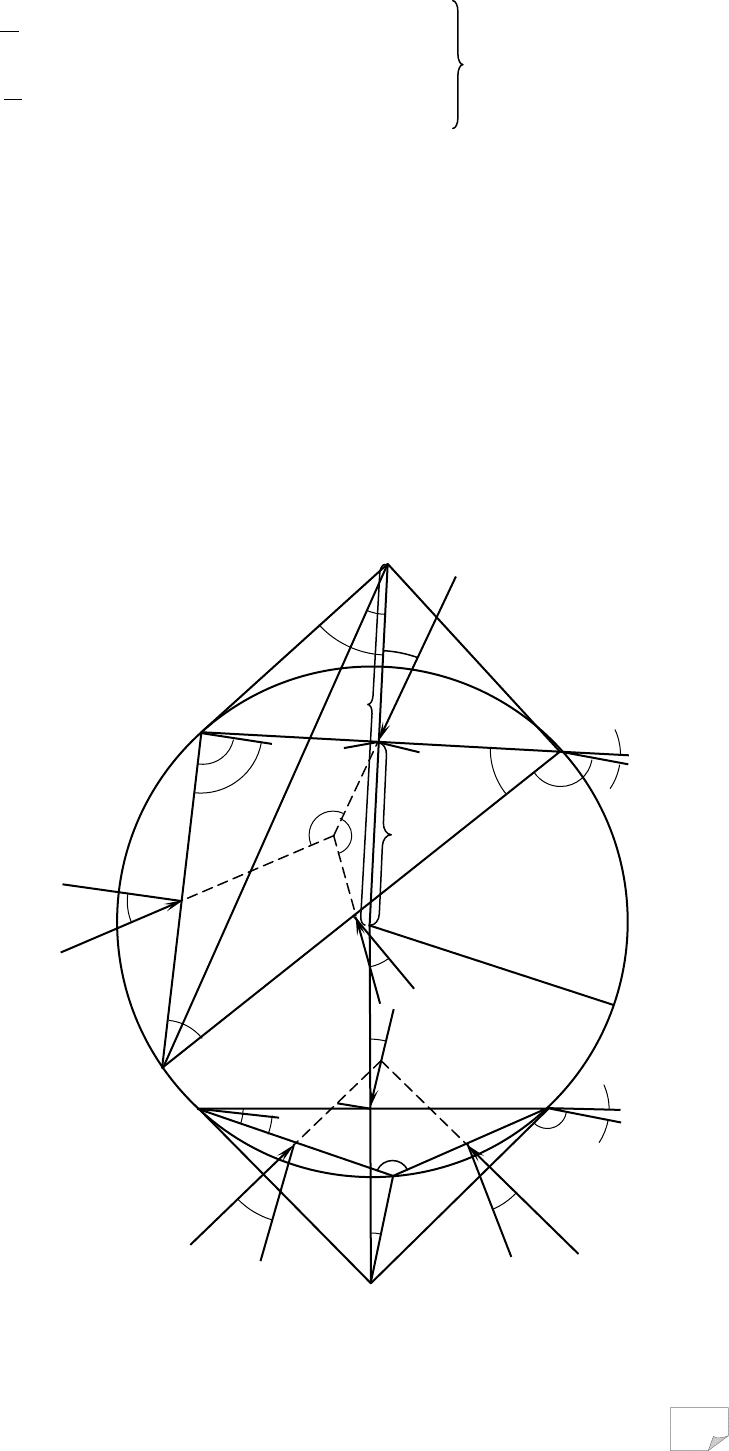
Розглянемо граничну рівновагу невагомої елементарної призми ABD, вважаючи, що

по площадці АВ розподілені наведені напруги, рівнодіюча яких F відхилена від нормалі до

площадки під кутом δ. Окрім того, будемо вважати AD i BD площадками ковзання. Відносно

осі відліку AB, AD та BD орієнтовані відповідно під кутами β

, β

(рис. 9.4). Тоді згідно з

годографом φ(β) відповідні кути внутрішнього тертя будуть φ(β

), φ(β

) та φ(β

Побудуємо навкруги призми коло з центром у точці О, з котрої проведемо перпенди-

куляр до площадки АВ. На останньому знайдемо точку, де перетинаються дотичні до круга,

проведені через кінці площадки АВ. Оскільки масштаб побудови довільний, будемо вважати,

що круг 3 відповідає кругу вершин, тобто його радіус дорівнює d/2 відповідно позначенням

п.9.1, і тоді виконана побудова збігається з наведеною у попередньому розділі.

Таким чином, якщо призма ABD знаходиться у граничному напруженому стані, кут

ρ=φ(β

). У протилежному випадку круг вершин, що є геометричною подобою кола Кулона–

Мора, не буде граничним, що суперечить вихідній передумові. Звідси виходить, що точка О

розташована на огинаючій характеристичних кіл площадок, а О

– на огинаючій кіл полюсів.

Крім того, якщо ABD відповідає мінімальному напруженому станові (а – на рис. 9.4), то кут

(9.12)

(9.13)

209

f=π/2-φ(β

), якщо максимальному (б – на рис. 9.4), то f=π/2+φ(β

), а ν та μ можна визначити за

допомогою залежностей

[ ]













±+±=

)(sin/sinarcsin)(,

1111

βϕδδβϕ

;

[ ]













±−±=

)(sin/sinarcsin)(,

1111

βϕδδβϕ

де верхні знаки відповідають напруженому станові а, нижні – стану б.

Повертаючись до розгляду граничної рівноваги ABD, відзначимо, що оскільки AD й

AB – площадки ковзання, то F

i F

відхилені від нормалей відповідно під кутами φ(β

) та

φ(β

) і проходять через середини відрізків AD та BD із причини невагомості основи.

З умови рівноваги ABD виходить, що пряма F повинна проходити через точку е пере-

тину F

i F

. Оскільки на вид годографу φ(β) обмеження не введені, то в загальному випадку

δ≠δ

. Звідси виходить, що для анізотропного ґрунту принцип сполученості площадок ковзан-

ня несправедливий. Ця обставина значно ускладнює вирішенння основної задачі у зіставлен-

ні з подібним для ізотропного ґрунту. Дійсно, заданому δ може відповідати декілька значень

, при яких F

i F

, відхилені від нормалей під відповідними кутами внутрішнього тертя, бу-

дуть перетинатися в одній точці з напрямом F. Отже при розв’язанні практичних задач необ-

хідно використовувати екстремальний принцип механіки.

Побудова, виконана на рис. 9.4, по суті є графічним вирішенням основної задачі для

анізотропного за опором зрушенню ґрунту. Наведемо послідовність процедур:

у довільному масштабі

будують площадку АВ, яка

зорієнтована під заданим ку-

том β

до осі відліку вихідного

годографа φ(β);

із точки перетину про-

меня з точки А під кутом φ(β

)

із нормаллю до площадки АВ,

тобто з точки О, будуємо коло

(радіус позначаємо d/2), що

проходить через точки А і В;

на колі вибираємо до-

вільну точку D і з’єднуємо її з

кінцями відрізку АВ;

за кутами орієнтації β

і β

з годографа φ(β),

з’ясувавши φ(β

) й φ(β

), нано-

симо напрямки F

та F

, які

прикладені у серединах відпо-

відних відрізків;

лінії дії F, F

, F

по-

винні перетинатися в одній

точці, у іншому випадку пере-

ходимо до наступної точки D

на колі 3, тобто шляхом пос-

лідовного набору точок D у

підсумку приходимо до мож-

ливих вирішень, серед яких

залежно від конкретної задачі

відшукують екстремальне.

За необхідності вирі-

(9.14)

d/2

а)

φ(β

)

φ(β

)

φ(β

)

φ(β

)

б)

Рис. 9.4. Графічне вирішення основної задачі для анізо-

тропного за опором зрушенню ґрунту