Зоценко Н.Л. Инженерная геология. Механика грунтов, основания и фундаменты

Подождите немного. Документ загружается.

230

Іншим різновидом фізичної нелінійності є однобічні зв’язки, тобто безперешкодний

розвиток деформацій одного знаку (стиснення-розтягнення) та збереження несучої здатності

при сприйманні нормальних напруг іншого напрямку. Прикладами конструкцій, що сприй-

мають лише стиснення, можуть бути контактні поверхні під плитою фундаментів, бічні по-

верхні паль, які відокремлюються при вигині від ґрунтової основи, матеріал навколо тріщин

тощо. Лише на розтягнення працюють конструкції типу вант, струн, затяжок. Іноді однобічні

зв’язки ще відносять до конструктивної нелінійності.

Ще один вид фізичної нелінійності, характерний саме для ґрунтів, – зрушення (сков-

зання) за деякою поверхнею, котра або визначається розрахунком, або умовами геотехнічної

задачі (наприклад, площина контакту підошви фундаменту та ґрунтової основи, межа геоло-

гічних нашарувань, поверхня ковзання ґрунтового укосу тощо).

Геометрична нелінійність звичайно проявляється у поздовжньому вигині централь-

но- і позацентрово стиснутих стрижнів (наприклад, паль) через ексцентриситет дії поздовж-

ньої сили, що виникає при відхиленні від положення рівноваги.

Іншою формою геометричної нелінійності є такий розвиток деформацій у суцільних

масивах, коли втрачає силу припущення про мализну розрахункових переміщень порівняно з

розмірами розрахункової області. В цьому випадку враховують зміни при деформуванні міс-

цезнаходження (координат) точок розрахункової області. Приклад рішення такої задачі (ма-

тематичне моделювання НДС основ фундаментів при їх зведенні без виймання ґрунту за різ-

ними технологіями та наступній роботі) наведено у п. 10.5.

Зміст поняття нелінійної деформативності ґрунтів і будівельних конструкцій також

тісно пов’язаний із можливістю настання їх граничних напружених станів (див. розділ 8).

Тому й теорії нелінійного деформування, що використовують для розв’язання задач механіки

ґрунтів, містять комплекс перевірок за граничними станами.

Сучасні методи розрахунків дозволяють успішно вирішувати інженерні задачі з ура-

хуванням різних проявів нелінійності. Для цього складені стандартні багатоцільові процеду-

ри послідовних наближень або кроків прикладення сил, у яких в якості обчислювальної ос-

нови використовують числові методи (див. п. 10.4). Зазначимо, що, на відміну від теорії

пружності, нелінійні задачі не мають єдиного рішення. За теорією пластичності поведінка

різних матеріалів, у тому числі ґрунту, описують різними рівняннями. Кожне рішення нелі-

нійної задачі являє собою версію відомої багатоцільової процедури у поєднанні з фізичними

рівняннями, що описують поведінку конкретних матеріалів і конструкцій з відхиленнями від

співвідношень теорії пружності.

10.2. ТЕОРІЇ, ЯКІ ОПИСУЮТЬ

НЕЛІНІЙНІ ДЕФОРМАЦІЇ ҐРУНТІВ

У загальному вигляді коректні теорії, що описують нелінійні деформації ґрунтів, ба-

зуються на таких уявленнях (Д. М. Шапіро, 1996):

- елементарний об’єм (елемент) ґрунту при зростанні навантаження проходить стадії

дограничного й граничного (пластичного) напружених станів, що визначаються фізичними

рівняннями теорії пружності та пластичності;

- через нерівномірний розподіл напруг у ґрунтовому масиві мають місце обидва види

напруженого стану, які локалізуються в зонах (ділянках), границі яких можливо встановити

розрахунком;

- граничні стани (втрата стійкості, прогресуючі переміщення) є наслідком розвитку

пластичних областей і накопичення характерних для них деформацій.

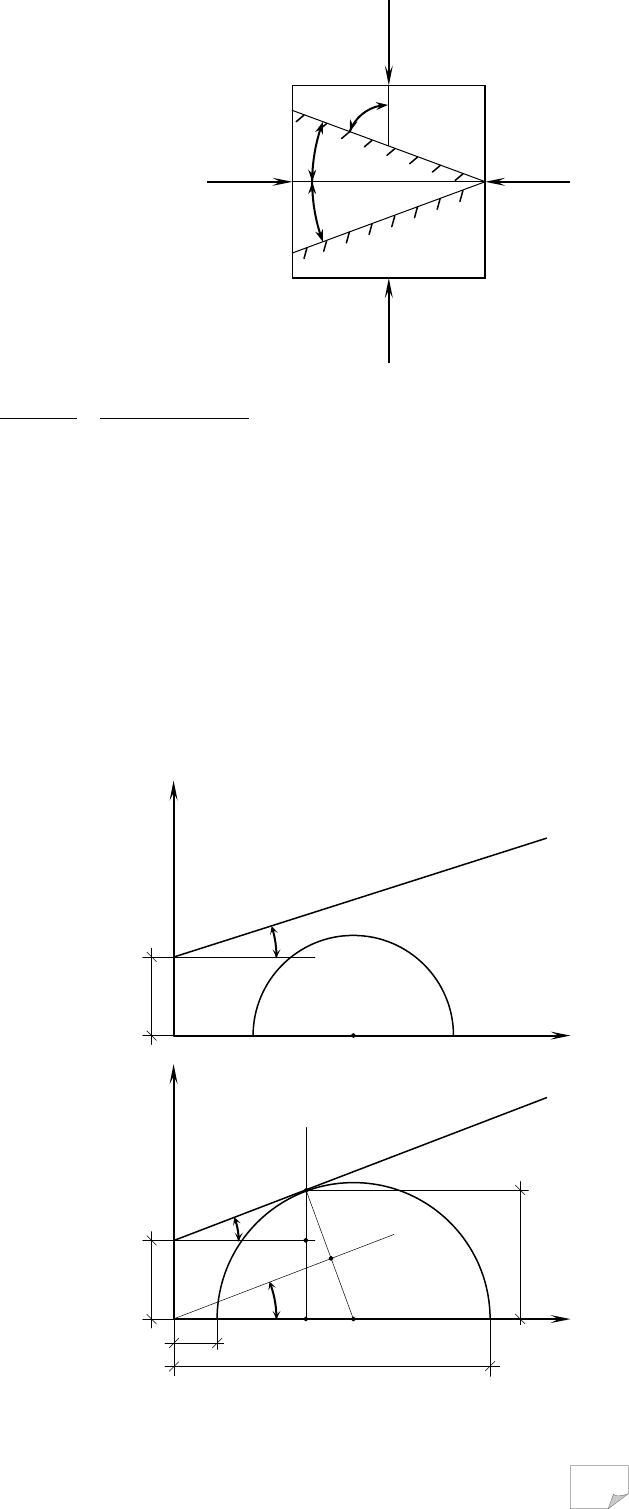
Звичайно ґрунт приймають за суцільне ізотропне середовище. Для таких тіл напруже-

ний стан у точці на площині однозначно визначається парою головних напруг σ

і σ

(рис. 10.2), а при просторовому напруженому стані – трьома головними напругами σ

, σ

Вважають, що для ґрунту характерні два види нелінійності: 1) безперешкодне деформування

при розтягненні; 2) пластична формозміна при складному напруженому стані (стиснення із

231

зрушенням).

Зв’язок між напругами та деформаціями визначає

прийнята модель ґрунту (згадайте п. 6.4), зокрема гра-

фік залежності між напругами та деформаціями досить

популярної у нелінійних задачах механіки ґрунтів моде-

лі ідеального пружно-пластичного тіла – лінія 3 на

рис. 6.11. Із нього видно, що загальні деформації вклю-

чають лінійну (пружну) і пластичну частини, причому

пластична складова деформацій виникає після досяг-

нення напруженим станом межі пропорційності (теку-

чості, міцності).

За межу пропорційності у точці (елементарному

об’ємі) масиву для умови плоскої деформації викорис-

товують рівняння Мора-Кулона у вигляді

2121

=−

−

ϕσσσσ

cosc

sin)(

(10.1)

На рис. 10.3 графічно проілюстрована умова міцності Мора-Кулона. Пряма АВ, що

уособлює закон Кулона (див. п.4.6), суміщена з кругами Мора, які показують три якісно різні

напружені стани в точці. Розташування круга Мора з центром у точці О

нижче від прямої

АВ означає, що ліва частина рівняння (10.1) менша від правої; на всіх площадках, котрі про-

ходять через точку, що розглядається, виконується умова

ctg

ϕστ

; межа пропорційно-

сті не досягнута; міцність ґрунту забезпечена.

Дотик прямої АВ до кола Мора з центром у точці О

показує, що на двох помічених

штрихуванням площадках елементарного об’єму на рис. 10.2 має місце гранична рівновага,

що характеризується залежністю

ϕσ

, і ці площадки нахилені до осей головних

напруг під кутами 45°±φ/2. Рівняння (10.1) може бути отримано з геометричних побудов для

цього кола: О

С=О

D+DC; О

С=(σ

-σ

)/2;

D=sinφ(σ

-σ

)/2; DC=c·cosφ. Відповідно до

цих же побудов на площадці сковзання

(рис.10.3) дотична напруга

→

дорівнює

сумі відрізків

cFL

→

та

ϕσ tgLC

→

)CLFLFC(

→→→

або

ctg

ϕστ

– закон Ку-

лона.

Коло Мора не може перетинатися пря-

мою, що виражає закон Кулона, бо ґрунт не

сприймає такий напружений стан. Якщо ж за

розрахунком таке ж положення все ж отрима-

не, то це свідчить про недосконалість методу

визначення компонентів напруг у ґрунтовому

середовищі. Рівняння (10.1) пояснює руйнуван-

ня ґрунту не як взаємне зміщення частин сипу-

чого тіла (за Кулоном), а як результат формо-

змінного впливу прикладених сил.

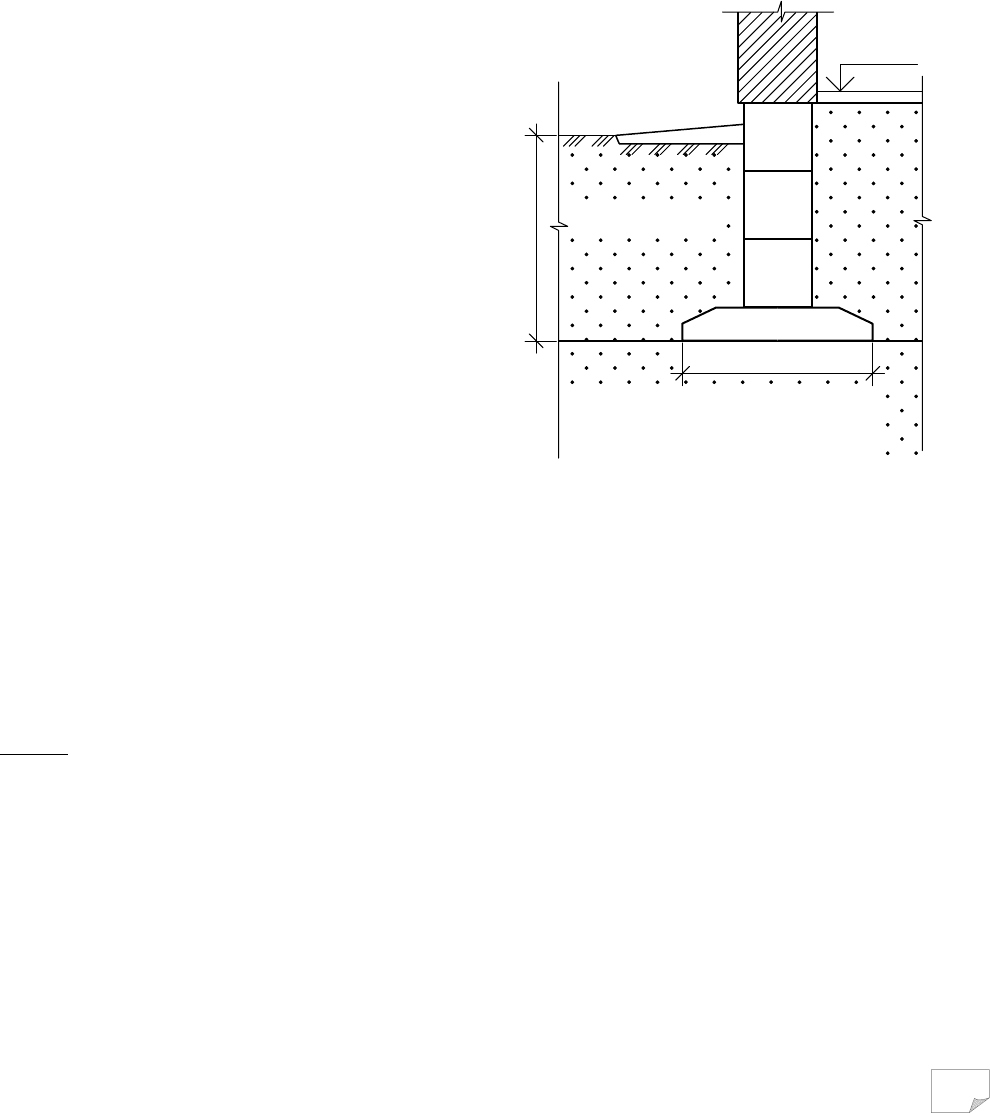
На рис. 10.4, а зображена площина голо-

вних напруг σ

1,2

. Кожна точка М(σ

, σ

) на пло-

щині зображає поєднання σ

та σ

, отже, один із

напружених станів в елементарному об’ємі ґру-

нту. Враховуючи, що у даному випадку можливі

45°-φ/2

45°+φ/2

Рис. 10.2. Напружений стан у

точці (елементарному об’ємі)

ґрунтового масиву

Рис. 10.3. Графічна ілюстрація умови

міцності Мора-Кулона

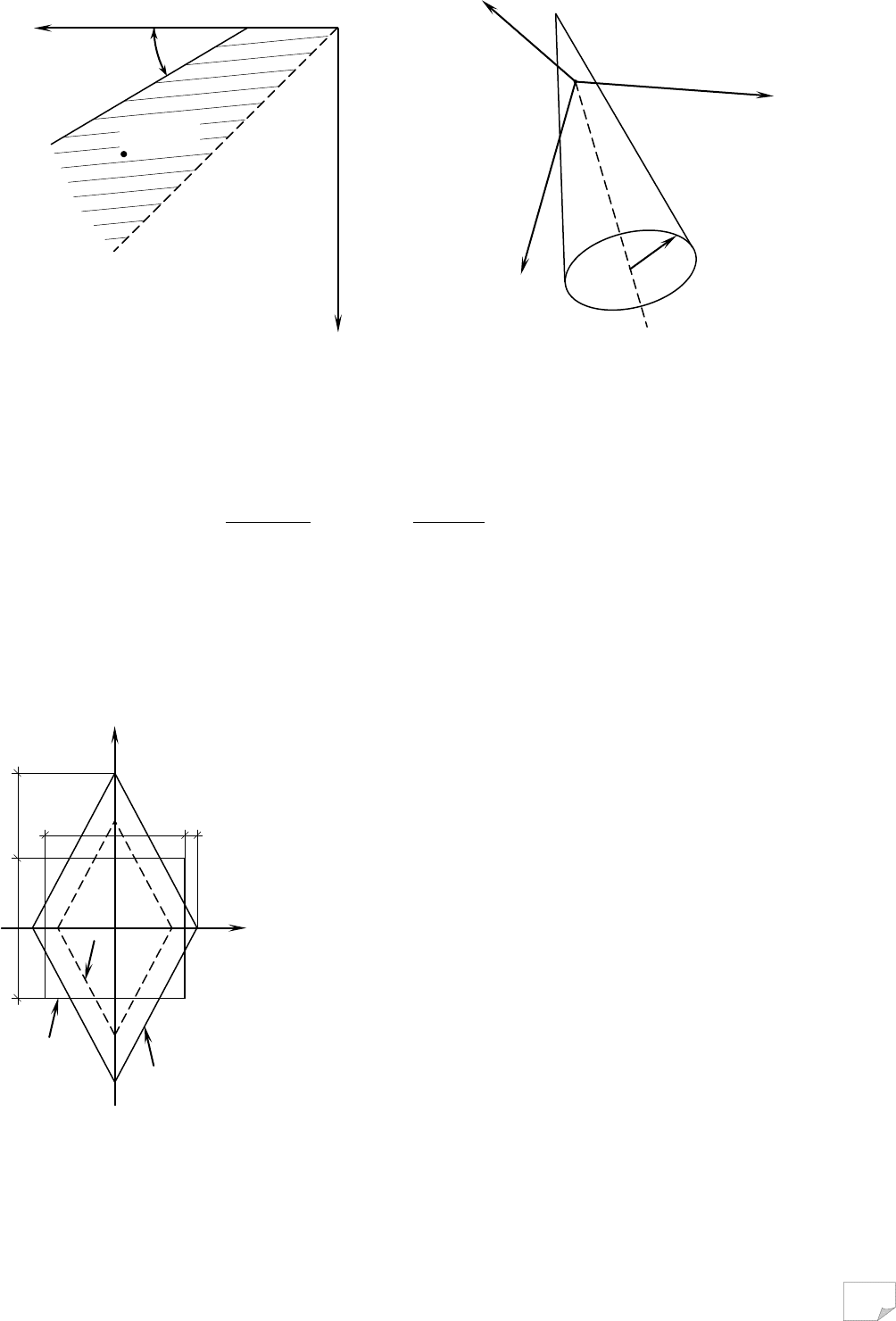
232

лише стискаючі напруги (σ

1,2

≤0), розглядають четвертину площини, обмежену від’ємними

напрямами осей σ

та σ

. Відповідно до прийнятого σ

≥σ

частина площини нижче від гідрос-

татичної осі ОС (де σ

=σ

) – недійсна.

Якщо позначити F=(σ

-σ

)/2+(σ

+σ

)(sinφ)/2-c·cosφ, то лінія АВ (рис.10.4, а) зображає

вираз (10.1) F=0; (

sin

cosc

−

⋅

−=

→

sin

arctg

−

); точки, розміщені над нею, зобража-

ють напружений стан із порушенням умови F≤0 і закону Кулона. Таким чином, область ф і-

зично можливих сполучень σ

та σ

на рис. 10.4, а обмежена фігурою ВАОС. Напружений

стан на межі ВАО, що характеризується рівняннями F=0, σ

=0, вважають граничним; його

виникнення у точці ґрунтового масиву вказує на зародження пластичної підобласті й перехо-

ду від пружної до пружно-пластичної стадії деформування.

У тілі Гука напрямок векторів головних напруг (σ

1,2

) і головних відносних деформацій

(ε

1,2

) збігаються або співвісні (коаксіальні). На стадії пласти-

чної течії вектори напруг та деформацій також приймають

співвісними. Однак у цьому випадку цю властивість уводять

не як наслідок відомих рівнянь, а у якості самостійного при-

пущення, підтвердженого дослідними даними. Отже, також

співвісні вектори пружних і пластичних складових головних

деформацій ε

1,2

. Пластичне деформування елементарного

об’єму ґрунту відбувається відповідно до схеми, що зображе-

на на рис. 10.5 за рівнянням

)(

±=

∗

Λλε

, (10.2)

де

– пластична складова головних деформацій ε

1,2

; λ –

мала скалярна величина, яка чисельно дорівнює куту зру-

шення,

/)(

εελ

−=

;

∗

– швидкість (параметр) дилатан-

сії (постійна, що відображає зміну об’єму при формозміні

(зрушенні) ґрунту). З рівняння (10.2) виходить, що

)/()(

nnnn

2121

εεεεΛ

−+=

∗

Коефіцієнт

0≠

∗

відрізняє форму деформації відпо-

відно до (10.2) від чистого зрушення (

∗

), де

λε

±=

, а

на площадках, нахилених до осей головних напруг під кутом



, має місце

/π

λεεγ

=−⋅=

)(,

nnn

214

Рис. 10.4. Області фізично можливих напружених станів:

а – на площині; б – у просторі

-σ

M(σ

)

-σ

б)

а)

1/2

2/2

Рис. 10.5. Формозміна та ди-

латансія елементарного об’є-

му ґрунту при пластичному

деформуванні: 1 –

початкові

розміри; 2 –

чисте зрушення

(Λ

∗

=0); 3 – формозміна з ди-

латансією (Λ

∗

>0)

233

Напружений стан у точці ґрунтового масиву, що описується трьома головними напру-

гами σ

, σ

, зображено на рис. 10.4, б. Графічною формою граничних напружених станів є

конічна поверхня із віссю ОС (σ

=σ

), яка утворює з напрямами координат кут 120°.

Слід також додати, що для характеристики складного напруженого стану часто вико-

ристовують так званий параметр Надаї-Лоде

312

σσ

σσσ

−

−−

. (10.4)

Для найпростіших напружених станів цей показник має такі значення: при одноосьо-

вому стисненні (σ

>0, σ

=σ

=0) і при трьохосьовому симетричному стані (σ

>σ

=σ

>0) він до-

рівнює μ

=-1; у випадку одноосьового розтягу (σ

=σ

=0; σ

<0) або при осьовому трьохосьо-

вому напруженому стані (σ

=σ

>σ

), μ

=+1; при чистому зрушенні (σ

=σ

>σ

, σ

=0) або коли

(σ

=0,5(σ

+σ

)>0), μ

=0. Напружений стан вважають подібним, якщо параметр μ

для цих ви-

падків однаковий.

10.3. ПРАКТИЧНІ МЕТОДИ УРАХУВАННЯ НЕЛІНІЙНОЇ

ДЕФОРМАТИВНОСТІ ҐРУНТІВ У РОЗРАХУНКАХ ОСНОВ

Методи розрахунку осідань, розглянуті у розділі 7, базуються на засадах теорії ліній-

ного деформування ґрунтів і справедливі за умови, що повний тиск за підошвою фундаменту

не перевищує розрахункового опору ґрунту (p≤R). Іноді, особливо при будівництві на щіль-

них ґрунтах, розраховане при цій умові осідання виявляється набагато менше від її гранич-

ного значення S<<S

. Тож для прийняття більш економічних розмірів фундаменту можна бу-

ло б дещо збільшити тиск під його підошвою. Та при цьому оцінка нового осідання методами

теорії лінійного деформування ґрунтів вже не буде об’єктивною.

Розрахунок осідань за межами лінійного деформування ґрунтів (при p>R) досить

складний і виконується переважно числовими методами на ЕОМ (п.10.4, 10.5). З інженерних

методів найбільшою популярністю в проектувальників користуються підходи професорів

М. В. Малишева та О. К. Бугрова.

Метод М. В. Малишева полягає у використанні аналогії між кривими “осідання – на-

вантаження” й “осідання – напруга”. Приймають, що при p≤R залежність між осіданням і на-

вантаженням практично лінійна. При p=p

, де p

– граничне критичне навантаження, осідан-

ня вважають рівним нескінченності. Отже, задача зводиться до пошуку певної функції, що

описує криволінійну ділянку залежності осідання від навантаження в інтервалі від p=R до

p=p

Із використанням положень теорії граничної рівноваги для визначення осідання S

за

межею лінійної деформативності ґрунтів застосовують залежність













−−

)pp)(R(

)Rp)(Rp(

uzg

, (10.5)

де S

– осідання основи при p=R; p

– граничний опір ґрунту основи, котрий визначають як

відношення вертикальної складової сили граничного опору до наведеної площі фундаменту

/(b′ℓ′) (див. п. 8.3); σ

zg0

– вертикальна напруга від власної ваги ґрунту на рівні підошви

фундаменту.

З аналізу вигляду формули (10.5) бачимо, що при p=R маємо S

, а при p=p

маємо

→∞. Отже, цей вираз відповідає прийнятим вище граничним умовам.

Формула (10.5) справедлива для однорідних ґрунтів у межах стислої товщі. В разі не-

однорідного нашарування визначають товщу z

, у межах якої знаходять середні розрахункові

характеристики ґрунтів

)p/(ESz

, (10.6)

де

m/E β

– середнє значення модуля деформації ґрунтів у межах стислої товщі;

– се-

234

реднє зважене значення відносного коефіцієнта стисливості шаруватої товщі, знаходження

якого аналогічно визначенню середньозваженого модуля деформації ґрунту в методі

І. О. Розенфельда (п. 7.7); β=0,8 – безрозмірний коефіцієнт; p

– додатковий вертикальний

тиск на основу під підошвою фундаменту. Якщо z

менше від ширини підошви фундаменту,

приймають z

=b.

Середні розрахункові характеристики (

), необхідні для визначення N

, для не-

однорідних нашарувань допускається визначати з умови

∑∑

iii

hhrr

, (10.7)

де r

– відповідно γ

, c

чи φ

кожного i-го шару; h

– товщина цього шару в межах товщі осно-

ви, що дорівнює z

Розрахунок осідань за межею прямої пропорційності за цим методом виконують у по-

слідовності: 1) звичайним способом, наприклад пошаровим підсумовуванням, розраховують

осідання фундаменту при p=R (якщо при цьому S<<S

, то призначають нову, меншу ширину

фундаменту і для неї визначають нове значення p, яке буде вже більше від R); 2) за формула-

ми (10.6) та (10.7) находять значення z

і середніх характеристик

; 3) для нового роз-

міру фундаменту з урахуванням цих характеристик визначають значення p

й за (10.5) розра-

ховують осідання S

(при цьому необхідне виконання умови S

≤S

Із прикладом застосування методу професора М. В. Малишева ми радимо ознайоми-

тись за “Пособием по проектированию оснований зданий и сооружений (к СНиП 2.02.01-

83)”. – М.: Стройиздат, 1986 (стор. 138-140).

Професор О. К. Бугров запропонував інший розрахунок осідань S

пл

основи з розвине-

ними ділянками граничного напруженого стану ґрунту. Він ґрунтується на використанні ве-

личин осідань S пружної (лінійно-деформівної) основи, коефіцієнта “пластичного” осідання

пл

та значення несучої здатності основи, при вичерпанні якої осідання наближається до не-

скінченності. Значення коефіцієнта

S/SK

пл

установлені узагальненням результатів

змішаних задач плоскої деформації для однорідних основ. За цим способом осідання пруж-

но-пластичної основи знаходять за формулою

плпл

SKS

, (10.8)

у якій коефіцієнт

пл

приймають за табл. 10.1 залежно від кута внутрішнього тертя φ

ґрун-

ту основи та величини x:

Таблиця 10.1. Значення коефіцієнта “пластичного” осідання

пл

Кут внутрішнього тертя φ

, град

0,1

0,2

0,3

0,4

0,5

0,6

0,7

0,8

0,9

0,99

1,00

1,14

1,32

1,56

1,86

2,30

2,95

4,03

6,20

12,70

129,70

1,00

1,10

1,24

1,39

1,57

1,81

2,13

2,60

3,43

5,34

21,00

1,02

1,08

1,18

1,28

1,41

1,55

1,74

2,01

2,41

3,25

15,30

1,02

1,08

1,18

1,26

1,40

1,51

1,70

1,92

2,30

3,00

12,10

1,03

1,08

1,16

1,25

1,35

1,47

1,61

1,80

2,08

2,61

10,50

1,04

1,08

1,16

1,24

1,33

1,43

1,55

1,72

1,96

2,37

9,40

1,05

1,09

1,16

1,23

1,31

1,39

1,50

1,66

1,86

2,22

8,72

1,06

1,09

1,17

1,23

1,30

1,37

1,46

1,60

1,73

2,07

7,80

1,06

1,09

1,17

1,23

1,29

1,35

1,43

1,53

1,67

1,92

7,10

Примітка. Кореляційним аналізом даних таблиці 10.1 А. В. Яковлєв отримав рівняння:

[ ] [ ]

)kk(x/)kk(K

4I32I1

пл

+ϕ⋅−−ϕ⋅=

;

-0,00731;

1,06007;

0,01029;

1,051.

235

)K/()K(x

гр

11 −−=

; (10.9)

R/pK

гр

, (10.10)

де p – середній тиск на основу за підошвою фундаменту; p

– граничний тиск на основу

/(b′ℓ′); R

=R – розрахунковий опір ґрунту, що визначають за формулою (12.1), коли

значення коефіцієнтів γ

=γ

=k=1,0.

Послідовність розрахунку, коли p>R, така: 1) визначають розрахункові характеристи-

ки ґрунтів вище і нижче від підошви фундаменту; 2) знаходять розрахункові опори ґрунту R

та R

; 3) визначають осідання S основи від середнього тиску p, наприклад за методом поша-

рового підсумовування; 4) розраховують граничний тиск p

на основу; 5) визначають вели-

чини

гр

і x; 6) за значенням x та φ

у таблиці 10.1 знаходять коефіцієнт

пл

; 7) визна-

чають осідання з урахуванням пластичної деформації S

пл

; 8) перевіряють умову p≤p

/γ

, де

і γ

– коефіцієнти умов роботи й надійності.

Приклад 10.1. Знайти розмір стрічкового

фундаменту з урахуванням розвитку в ґрунті діля-

нок граничного напруженого стану. Фундамент

під несучі цегляні стіни багатоповерхового будин-

ку розміщується на потужному шарі маловологого

пилуватого піску з характеристиками: γ

=18,0

кН/м

, γ

=17,5 кН/м

, c

=2 кПа, c

=1,5 кПа, φ

=30°,

=28°,

20,0 МПа. Глибина закладання фунда-

менту

1,8 м (розрахункову схему див. на

рис. 10.6). Питома вага ґрунту засипання

γ′

=γ′

=18 кН/м

. Навантаження від фундаменту

0,72 МН на 1 м довжини. Граничне осідання буді-

влі цього типу S

=10 см (дод. 4 СНиП 2.02.01-83

За табл. 3 СНиП 2.02.01-83

приймаємо ко-

ефіцієнти γ

=1,2, γ

=1,0 і k=1,0, а за табл. 4 – ко-

ефіцієнти M

=1,15; M

=5,59; M

=7,95. Виходячи з

умови p≤R, визначаємо ширину фундаменту. Вона

складає

2,4 м. При цьому p=R=0,3 МПа. Роз-

рахунок осідання цього фундаменту методом по-

шарового підсумовування (див дод. 2 СНиП

2.02.01-83

) дає глибину стислої товщі H

=9,2 м та осідання S=4 см, що значно менше ніж

=10 см. Тому пропонується розглянути можливість переходу на фундамент із шириною

підошви

1,6 м, яка передає на основу тиск

0,446 МПа.

Відповідно до алгоритму методу О. К. Бугрова для фундаменту з шириною підошви

1,6 м маємо:

- розрахунковий опір ґрунту за формулою (7) СНиП 2.02.01-83

0,1

0,12,1 ⋅

[1,15·1,0·1,6·18,0+5,59·1,80·18,0+7,95·2]= =277 кПа=0,277 МПа, а розрахунковий

опір ґрунту R

при коефіцієнтах γ

=γ

=k=1,0, R

=0,231 МПа;

- за методом пошарового підсумовування глибина стисливої товщі H

=9,8 м, а осі-

дання S=5,1 см;

- граничний тиск на основу (див. формулу (16) СНиП 2.02.01-83

)

/(′ℓ′)=6,5·17,5·1,6+14,1·18·1,8+26·1,5=676 кПа=0,676 МПа.

Визначаємо величини

=p/R

=0,446/0,231=1,93;

гр

R/pK =

=0,676/0,231=2,93;

)1K/()1K(x

гр

−−=

=(1,93-1)/(2,93-1)=0,48. За значенням x=0,48 і φ=30° у таблиці 10.1 зн а-

ходимо коефіцієнт

пл

=1,37. Осідання пружно-пластичної основи при тискові

0,446

b=1,6 м

d=1,8 м

E=20 МПа

γ′

=18 кН/м

=2 кПа

=30°

γ′

=18 кН/м

0,000

Рис. 10.6. Розрахункова схема до

прикладу 10.1

236

МПа складе

плпл

SKS =

=5,1·1,37≈7 см < S

=10 см.

При тискові p=0,446 МПа та значеннях коефіцієнтів надійності γ

=1,2 й умов роботи

=0,9 (див. п. 2.58 СНиП 2.02.01-83

) несуча здатність основи забезпечується із запасом:

p=0,446 <

505,0

2,1

9,0676,0

2,1

p9,0

⋅

МПа.

Таким чином, наведені розрахунки показують, що фундамент із шириною підошви

b=1,6 м може бути прийнято в якості проектного замість фундаменту з b=2,4 м.

Ці приклади підтверджують, що перехід на проектування фундаментів за деформаці-

ями основ, для ґрунту яких допускається робота в пружно-пластичній стадії, дозволяє при-

йняти дещо менші розміри фундаментів будівлі при збереженні необхідної несучої здатності

їх основ.

10.4. ТЕОРЕТИЧНІ ОСНОВИ ЧИСЛОВИХ МЕТОДІВ

Як видно з п. 10.1 та 10.2, деформування ґрунтів під навантаженням являє собою дуже

складний процес. Навіть при невеликому тискові їм притаманна нелінійна залежність між

напругами та деформаціями або фізична нелінійність. При цьому значний відсоток деформа-

ції містить у собі пластична складова (див. п. 4.5). До особливостей НДС ґрунтових масивів

відносять й одночасність існування в них областей, що перебувають у дограничному та гра-

ничному за міцністю стані. Природно, що властивості ґрунтів у цих зонах треба описувати

різними рівняннями стану. Крім того, звичайно масиви містять у собі шари ґрунту з різними

фізико-механічними властивостями. В межах зон із наведеними властивостями навколо фун-

даментів, що влаштовують без виймання ґрунту (див. п. 12.3), значення параметрів ґрунту

теж змінюються залежно від їх природних характеристик, а також конструктивних, техноло-

гічних особливостей фундаментів тощо. Наявна у реальних ґрунтів і природна та наведена

анізотропія (див. п. 4.10). Тобто для ґрунтових масивів характерна неоднорідність середови-

ща. Складні геометричні форми подекуди мають і контури фундаментів, підземних споруд,

границь шарів та зон ґрунтів тощо.

Зрозуміло, що винайти строгі аналітичні рішення для кожної з великої кількості задач

прогнозу напружено-деформованого стану ґрунтового масиву дуже складно. Тому в інжене-

рній практиці користуються методами, основаними на введенні спрощуючих передумов.

Найбільше поширення в механіці ґрунтів отримав метод кінцевих (або скінченних) елементів

(МКЕ), дещо менше – метод граничних елементів (МГЕ) й метод кінцевих різниць (МКР).

Метод кінцевих різниць. МКР найперший за часом із числових методів, що почав ви-

користовуватись у задачах механіки ґрунтів. Він орієнтований на розв’язання задач, що опи-

суються рівняннями в частинних похідних. Стосовно задач теорії граничної рівноваги МКР

широко застосовувався професорами В. В. Соколовським та В. А. Флоріним, а в розрахунках

напружено-деформованого стану основ у нелінійній постановці – Є. Ф. Винокуровим.

Ідея МКР – у заміні частинних похідних у диференційних рівняннях задач на відно-

шення різниці змінних, що називаються кінцевими різницями. Ось як професори С. Б. Ухов і

В. В. Семенов (1994) пояснюють зміст цього методу.

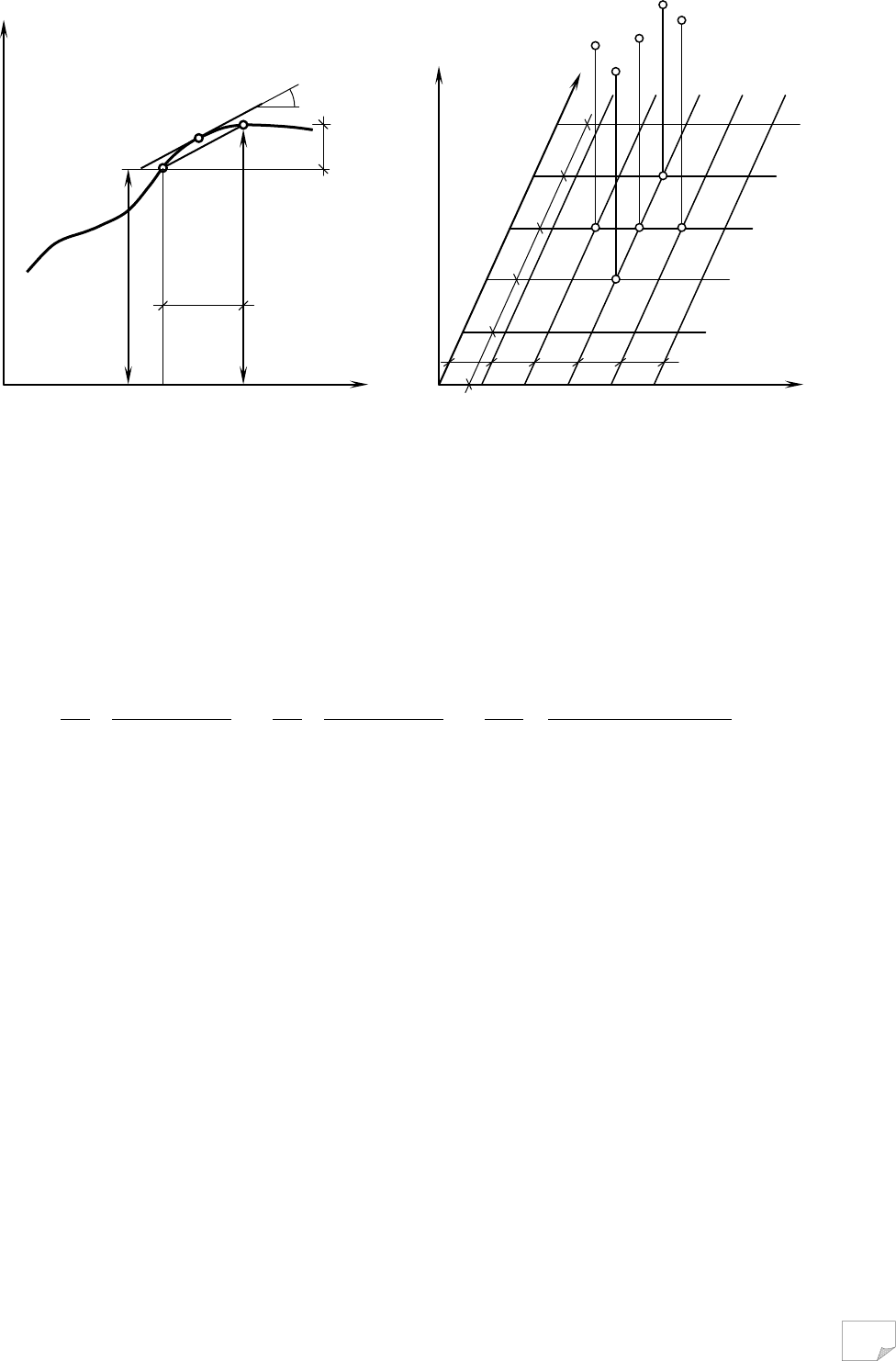
Нехай є певна функція φ від аргументу x (рис. 10.7, а). Похідна dφ/dx у певній точці А

дорівнює тангенсу кута нахилу дотичної у точці А до кривої φ(x), тобто dφ/dx=tgα. Виділимо

в оточенні точки А інтервал Δx достатньо малих, але кінцевих розмірів. Цьому інтервалу від-

повідає приріст функції Δφ. Тоді записуємо наближений вираз для похідної

xxxxdx

lim

−

=≅=

→

ϕϕ

∆

ϕ∆

∆

ϕ∆ϕ

∆

, (10.11)

причому вираз (10.11) буде тим точнішим, чим менший інтервал Δx. Якщо задача одновимір-

на й описується диференційним рівнянням, яке вміщує лише першу похідну функції φ(x), то

необхідно розділити інтервал зміни аргументу x на кінцеве число ділянок Δx, обмежених ву-

237

злами. Диференційні рівняння задачі можна перетворити, використовуючи співвідношення

типу (10.11), і записати їх для кожного вузла. Поставивши відповідні граничні умови, ми

прийдемо до системи рівнянь, число котрих дорівнює числу невідомих значень функції у ву-

злах.

При рішенні двовимірних задач будується кінцево-різницева сітка з кроками за відпо-

відними координатами Δx та Δy (рис. 10.7, б). Перетин ліній сітки також називають вузлами.

Частинні похідні функції φ(x,y), що залежать тепер від двох координат, у деякому вузлі i, j

можуть бути виражені через наближені кінцево-різницеві співвідношення:

j,ij,i

∆

ϕϕ

11 −+

−

≅

∂

;

j,ij,i

∆

ϕϕ

11 −+

−

≅

∂

;

)x(x

j,ij,ij,i

∆

ϕϕϕ

−+

+−

≅

∂

. (10.12)

Індексація при позначенні функції відповідає нумерації вузлів кінцево-різницевої сіт-

ки. Оскільки диференційні рівняння містять усі необхідні константи (зокрема, пружні харак-

теристики K та G у задачах теорії пружності), то ці константи входять і до кінцево-

різницевих співвідношень.

У підсумку диференційні рівняння крайової задачі заміняються кінцево-різницевими

співвідношеннями, що об’єднуються в систему лінійних алгебраїчних рівнянь. Уведення

граничних умов у вигляді фіксованих значень змінних чи їх похідних на границях розрахун-

кової області робить систему рівнянь визначеною. Найчастіше у якості невідомих у задачах

механіки ґрунтів фігурують переміщення, значення яких для кожного вузла кінцево-

різницевої сітки знаходяться в результаті рішення системи рівнянь відомими методами лі-

нійної алгебри. Через знайдені переміщення визначаються відносні деформації та напруги,

тобто задача про напружено-деформований стан виявляється розв’язаною.

Характеристики властивостей середовища можуть бути як однаковими за всією роз-

рахунковою областю, так і різними на окремих її ділянках. Це дозволяє вирішувати МКР за-

дачі для неоднорідних середовищ. До недоліків МКР відносять складності при відтворенні

границь розрахункової області й ділянок, які суттєво відрізняються за фізико-механічними

властивостями. Цей метод не набув такого значного поширення, як МКЕ.

Метод кінцевих (скінченних) елементів (цей пункт написано спільно з професором

С. Ф. Клованичем). МКЕ – потужний засіб розрахунку й теоретичного аналізу при проекту-

ванні будівельних конструкцій і споруд, перевірки адекватності конкретних моделей ґрунту

та обмеження областей їх застосування. Володіння цим методом становить незамінну части-

ну професійних знань інженера-проектувальника. Ідеї МКЕ були відомі ще на початку XX

φ(x,y)

Δx

Δy

Δx

i-1,j

i+1,j

i,j

i,j-1

i,j+1

i,j-1

i,j+1

i+1,j

i-1,j

i,j

φ(x)

Δx

Δφ

Рис. 10.7. Схеми до побудови кінцево-різницевих співвідношень:

а – для одновимірної; б – для плоскої задач

238

століття, та їх реалізація стала можливою в 60-х роках завдяки успіхам обчислювальної тех-

ніки.

Стосовно розрахунків основ і фундаментів вдалу апробацію пройшли прикладні про-

грами з використанням МКЕ, розроблені І. П. Бойком, О. К. Бугровим, Г. В. Васильковим,

О. Л. Гольдіним, А. Л. Готманом, В. О. Гришиним, Б. Й. Дідухом, М. М. Дубиною,

Ю. К. Зарецьким, С. М. Клепіковим, С. Ф. Клованичем, І. В. Матвєєвим,

Ш. Р. Незамутдіновим, Ю. І. Немчиновим, В. М. Ніколаєвським, О. О. Петраковим,

О. В. Пілягіним, В. С. Прокоповичем, С. Б. Уховим, О. Б. Фадєєвим, В. Г. Федоровським,

Д. М. Шапіро, В. Г. Шаповалом й іншими, програми вчених Нідерландів і США – PLAXIS,

DIANA, FLAC. Зараз МКЕ є головним та найбільш універсальним із числових методів, які

проклали шлях до повноцінного використання обчислювальних можливостей ЕОМ у проек-

туванні.

На думку професора І. П. Бойка МКЕ найбільш підходить для задач із розвиненою

неоднорідністю характеристик міцності. Порівняно з класичними варіаційними методами

МКЕ більш алгоритмічний і гнучкий при описі геометрії й граничних умов, фізично наочний

та універсальний для широкого кола задач механіки. Перевагами, що забезпечують популяр-

ність МКЕ в геомеханіці, є також: простота отримання конкретних рішень за програмою;

можливість згущення сітки КЕ в місцях, де очікують високі градієнти параметра, що дослі-

джують; принципова можливість реалізації в програмах довільних механічних властивостей

матеріалу, будь-якої послідовності навантаження; можливість оцінювання сумісної роботи

основ і фундаментів без поділу на незалежні розрахунки за несучою здатністю та деформаці-

ями тощо.

Основи МКЕ тепер викладають у курсі будівельної механіки (можна порекомендува-

ти книги В. А. Баженова, К. Бате і Є. Вільсона, О. С. Городецького, С. Ю. Єременка,

О. Зенкевича, І. М. Молчанова та Л. Д. Ніколенка, Д. Норрі і Ж. Де Фріза,

А. С. Перельмутера та В. І. Слівнера, А. С. Сахарова, Л. Сегерлінда, Р. А. Хечумова і

Х. Кепплера та інших). Додаток цього методу до задач механіки ґрунтів докладно вміщено в

монографіях: Ухов С. Б. Расчет сооружений и оснований методом конечных элементов. – М.:

МИСИ, 1973 та Фадеев А. Б., Прегер А. Л. Решение геотехнических задач методом конечных

элементов. – Томск: Изд-во Том. ун-та, 1994, а також у посібнику: Шапіро Д. М. Расчет

конструкций и оснований методом конечных элементов. – Воронеж: ВГАСА, 1996.

Переваги МКЕ як числового методу полягають у наступному: 1) розрахунки кон-

струкцій і середовищ, у т. ч. основ і фундаментів, зводяться до системи лінійних чи неліній-

них алгебраїчних рівнянь безпосередньо без попереднього формулювання їх диференційних

аналогів; 2) суцільне середовище розбивають на ряд елементів (КЕ), котрі можна розглядати

як його конкретні частини (до речі, ці елементи можна вибирати таким чином, щоб їх робота

відповідала умовам стандартних випробувань зразків ґрунтів чи матеріалів конструкцій);

3) основні процедури МКЕ стандартні й не залежать від розмірності та типів КЕ, що уніфікує

ці процедури й дозволяє складати програмні комплекси для розрахунку середовищ, констру-

кцій і споруд широкого класу та призначення.

Коротко розглянемо основні положення МКЕ. Маємо тверде деформоване тіло, що

знаходиться в рівновазі під зовнішнім впливом (рис. 10.8). Подумки розділимо його на КЕ.

Виділимо типовий i-тий КЕ й припустимо, що він знаходиться під впливом лише зусиль вза-

ємодії із суміжними КЕ, котрі викликані деформацією тіла. Ці сили відносно виділеного КЕ

розглядаємо як зовнішні. Якщо тіло – у рівновазі, то й цей КЕ – теж у рівновазі. Прикладемо

до нього замість реальних розподілених зусиль, які діють уздовж меж його стикування із су-

міжними КЕ, статично еквівалентні вузлові сили, отже, сили, дія котрих викликає у середині

КЕ НДС, аналогічний тому, що був би в ньому від фактичного навантаження. Сукупність

цих зусиль представимо вектором стовпцем

{ } { } { } { } { }

{ }

)m(

)k(

)(

R...R...RRR

, де

{ } { }

{ }

)k(

R...RRR

– вектор вузлових зусиль у k-му вузлі i-го КЕ, компонентами якого

є еквівалентні сили за напрямами 1, 2,…r. Поставимо у відповідність кожному вузловому

239

зусиллю вузлові переміщення та введе-

мо до розгляду вектор переміщень

{ } { } { } { } { }

{ }

)m(

)k(

)(

q...q...qqq

, де

{ }

...vuq...qqq

)k(

– век-

тор вузлових переміщень k-го вузла i-го

КЕ з компонентами переміщень по на-

прямку 1, 2,…r; r – ступінь вільності

вузла. Таким чином, суцільне тіло

представляють набором кінцевого чис-

ла елементів, які взаємодіють між со-

бою в кінцевому числі вузлових точок.

Інтерпретуючи суцільне середовище

таким чином, можна звести розрахунок

тіла до розрахунку системи з кінцевим

числом ступенів волі і, отже, визначити

вузлові зусилля чи вузлові переміщення

за процедурою, аналогічною за змістом

та алгоритмом процедурі розрахунку стрижневих систем методами будівельної механіки.

Для цього залишається знайти матриці жорсткості (податливості) для окремих КЕ, а потім

розглянути умови статичної та кінематичної сумісності сукупності КЕ, отримуючи тим са-

мим розв’язуюче рівняння задачі.

Знайдені вузлові переміщення (зусилля) не дають повної оцінки НДС континуальної

системи. Слід перейти до переміщень, деформацій та напруг у середині КЕ. За невідомі в за-

дачі вибирають вузлові переміщення (метод переміщень) або вузлові зусилля (метод сил).

Певну перевагу методові переміщень віддають через використання в його рішенні простого

матричного рівняння. При цьому кількість невідомих здебільшого виявляється менша, ніж у

методі сил, а матриця коефіцієнтів має стрічкову структуру. До того ж метод переміщень ві-

дрізняється простотою і стандартністю вибору основної системи.

Між векторами

{ }

та

{ }

існує взаємно однозначна відповідність

{ }

[ ]

{ }

qKR

, (10.13)

де

[ ]

– матриця жорсткості i-го елемента, яка має також і блочний вигляд

[ ]

[ ] [ ] [ ]













)m(

)k(

)(

)m(

)k(

)(

)m(

)k(

)(

K...K...K

...............

K...K...K

...............

K...K...K



. (10.14)

Кожен з блоків матриці

[ ]

)k(



визначає реакції в ℓ-му вузлі від одиничних перемі-

щень у k-му вузлі i-го елемента. Для отримання матриць жорсткості окремих КЕ розглянемо

питання про перехід від вузлових переміщень до переміщень, деформацій і напруг у середині

КЕ. Наближено він здійснюється задаванням інтерполяційних функцій, характер яких пови-

нен забезпечити нерозривність переміщень при переходу від елемента до елемента. При зме-

ншенні розмірів КЕ це повинно привести до більш точного рішення. Зв’язок між вузловими

переміщеннями й переміщеннями у середині КЕ записують у вигляді

{ }

[ ]

{ }

qCu

[ ] [ ] [ ] [ ]

[ ]

{ }

)m()k()()(

qC...C...CC

, (10.15)

де

[ ]

– матриця інтерполяційних функцій.

Якщо останнє співвідношення визначати за допомогою геометричного рівняння (Ко-

ші)

{ }

[ ]

{ }

uФ

, (де

[ ]

– матриця диференційних операторів) та фізичного рівняння

)k(

{ }

)k(

(k)

Рис. 10.8. Кінцевоелементна модель твердого тіла