Жлуктенко В. І., Наконечний С. І., Савіна С.С. Теорія ймовірностей і математична статистика: У 2-х ч. - Ч. ІІ. Математична статистика
Подождите немного. Документ загружается.

133
Висновок. Оскільки
[
]
3,13;0
2
сп
∈χ
, то не маємо підс-
тав для прийняття Н
0
про нормальний закон розподі-
лу ознаки генеральної сукупності Х.
Приклад. Вимірювання зросту юнаків віком 17 років дав
такі результати:
h = 4 cм 154—158 158—162 162—166 166—170 170—174 174—178 178—182 182—186
n
i
8 14 20 32 12 8 4 2
Визначити гіпотетично, який закон розподілу має ознакa
Х — зріст юнака. При рівні значущості α = 0,01 перевірити
правильність висунутої нульової гіпотези.
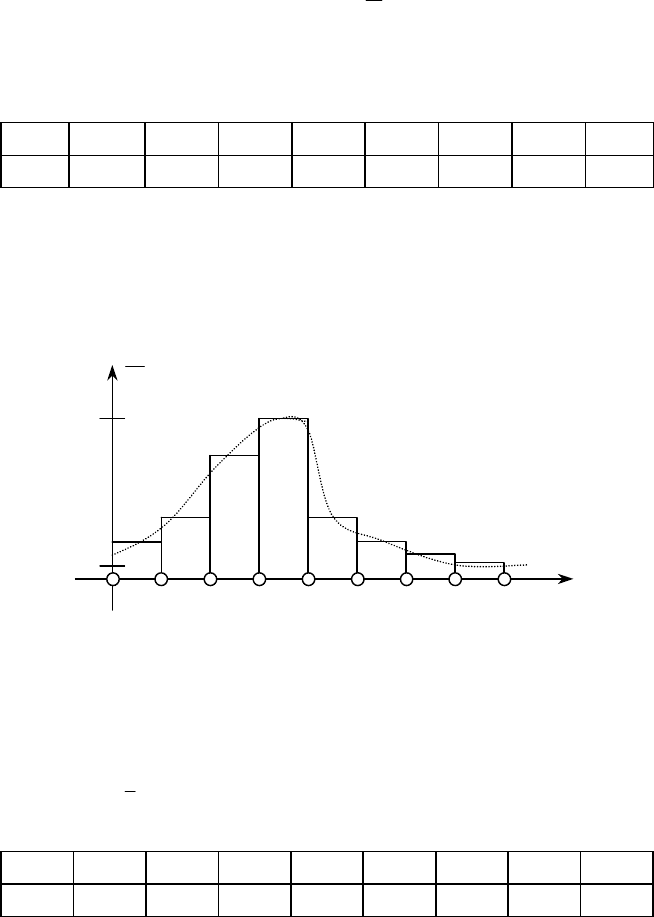
Розв’язання. Для заданого статистичного розподілу побудуємо гіс-
тограму частот (рис. 143).
186182178
174
170166162158
154
h
n
i
8
1
x
i
Рис. 143
За формою гістограми частот можемо припустити, що ознака Х має
нормальний закон розподілу. Отже, висуваємо нульову гіпотезу Н
0
:
ознака Х має нормальний закон розподілу ймовірностей.
Для перевірки правильності Н
0
використаємо критерій узгодженості
Пірсона.
Отже, необхідно обчислити теоретичні частоти, а для цього знайде-
мо значення
BB
σ,x
, побудувавши дискретний розподіл за заданим ін-
тервальним, а саме:
x
i
156 160 164 168 172 176 180 184
n
i
8 14 20 32 12 8 4 2
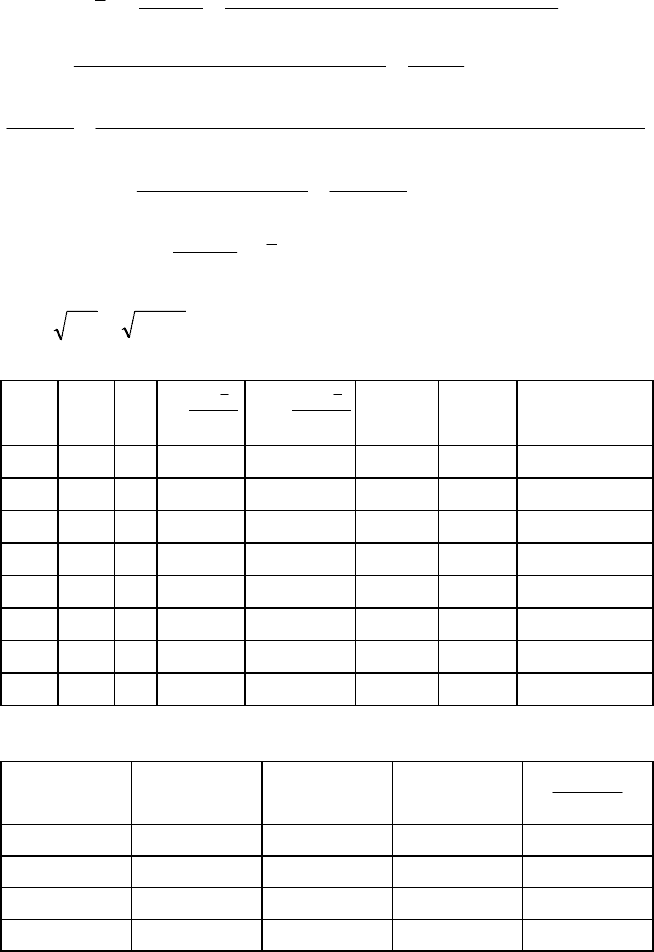
134
100
3216820164141608156 +⋅+⋅+⋅+⋅
=
∑
=
n
nx
x
ii
B
04,167
100
16704
100
21844180817612172
==
⋅
+
⋅
+
⋅
+⋅
+
cм;
;04,27943
100
2794304
100
21844180
100
8176121723216820164141608156
22
222222
2
==
⋅+⋅+
+⋅+⋅+⋅+⋅+⋅+⋅
=
∑
n
nx
ii
;68,403616,2790204,27943
)04,167(04,27943)(
22
2
=−=
=−=−=
∑
BB
x
n
nx
D
ii
38,668,40 ≈==σ
BB
D
см.
Обчислення теоретичних частот наведено в таблиці:
x
i
x
i+1
n
i
B
B
σ
−
=
xx
z
i
i
B
B
σ
−
=
+
+
xx
z
i
i
1
1
)(Ф
i
z
)(Ф
1+i
z
)
)
(
((
1
i
ii
zФ
zФnn
−
−
=
+
′
154 158 8 – 2,04 – 1,42 – 0,4793 – 0,4222 6
158 162 14 – 1,42 – 0,79 – 0,4222 – 0,2852 14
162 166 20 – 0,79 – 0,16 – 0,2852 – 0,0636 22
166 170 32 – 0,16 0,464 – 0,0636 0,1772 24
170 174 12 0,464 1,09 0,1772 0,3621 19
174 178 8 1,09 1,72 0,3621 0,4573 10
178 182 4 1,72 2,34 0,4573 0,4904 3
182 186 2 2,34 2,97 0,4904 0,4986 1
Обчислення спостережуваного значення
2
cп
χ наведено в таблиці:
n
i
np
i
n
i
– np
i
(n
i
– np
i
)
2
i
ii
np
npn
2
)( −
8 6 2 4 0,667
14 14 0 0 0
20 22 – 2 4 0,182
32 24 8 64 2,667
135
12 19 – 7 49 2,579
8 10 – 2 4 0,4
4 3 1 1 0,333
2 1 1 1 1
828,7
)(
8
1
2
2
сп
=
−
=χ
∑
=i
i
ii
np
npn
.
За таблицею (додаток 8) знаходимо значення
.1,15)5;01,0()128;01,0(
2
сп
2
сп
=χ=−−==αχ
k
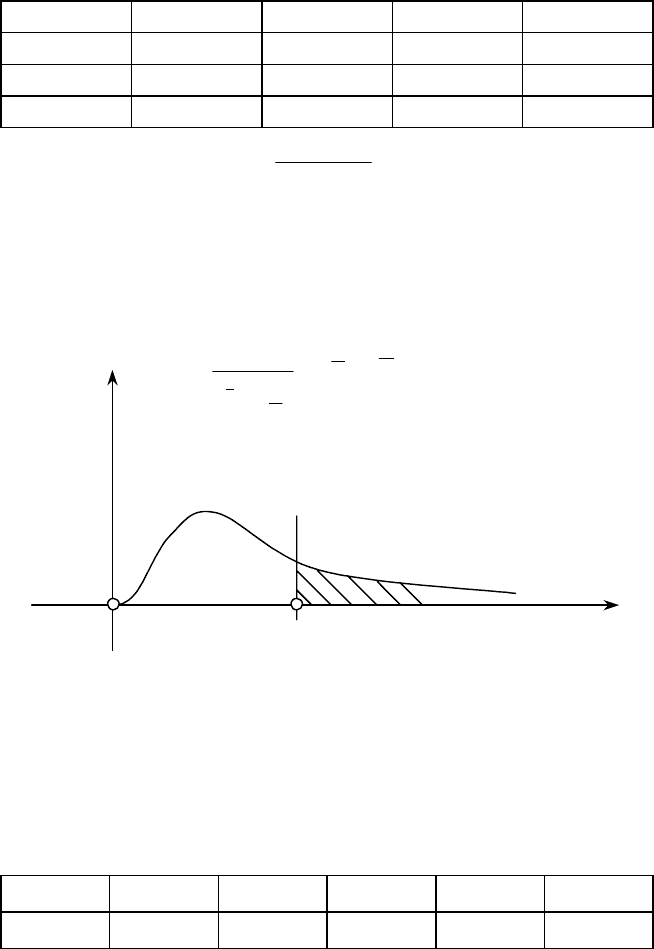
Критична область зображена на рис. 144.
()
2
1
2
2
2
2
2
2
2
Г2
1
)(
χ
−
−
χ
⎟
⎠
⎞
⎜
⎝
⎛
⋅
=χ e
k
f
k
k
χ
2
2
кр
χ
= 15,1
0
Рис. 144
Висновок. Оскільки
[
]
1,15;0
2
сп
∈χ
, немає підстав для
відхилення нульової гіпотези Н
0
про нормальний за-
кон розподілу ймовірностей ознаки Х.
Приклад. За заданим статистичним розподілом вибірки:
h = 4 cм
0—10 10—20 20—30 30—40 40—50
n
i
40 30 20 6 4
136
з’ясувати гіпотетично закон розподілу ймовірностей випа-
дкової величини Х. При рівні значущості α = 0,01 переві-
рити правильність цього припущення.
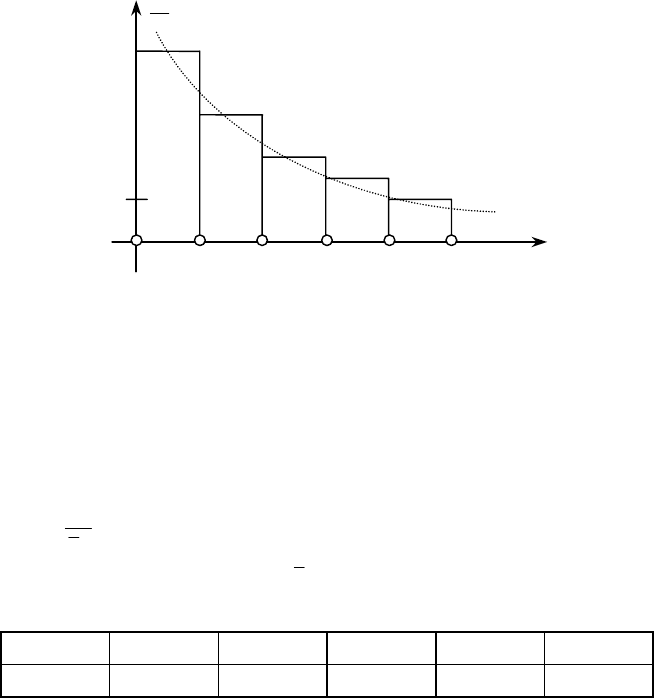
Розв’язання. Для визначення закону розподілу ознаки Х по-
будуємо гістограму частот (рис. 145).
4030
20100
1
50
x
i
4
h
n
i
Рис. 145
За формою гістограми частот можна гіпотетично стверджувати, що
ознака Х має експоненціальний закон розподілу ймовірностей.
Для перевірки правильності цього твердження використаємо крите-
рій узгодженості Пірсона. Теоретичні частоти в цьому разі обчислю-
ються за формулою
(
)
1+
λ−λ−
−=
′
ii
xx
i
eenn ,
де
B
x
1
=λ
.
Отже, необхідно обчислити
B
x , побудувавши дискретний статисти-
чний розподіл за наведеним інтервальним, а саме:
x
i
5 15 25 35 45
n
i
40 30 20 6 4
Оскільки
∑
== 100
i
nn
, то
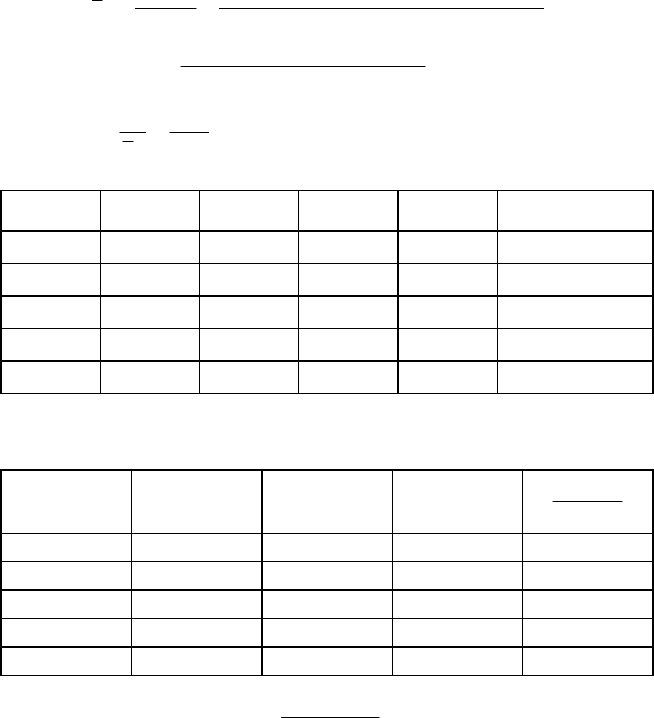
137
=
⋅+⋅+⋅+⋅+⋅
==
∑
100
44563520253015405
n
nx
x
ii
B
4,15
100
180910500450200
=
++++
=
.
Тоді
065,0
4,15
11
===λ
B
x
.
Обчислення теоретичних частот наведено в таблиці:
x
i
x
i+1
n
i
i
x
e
λ−
1+
λ−
i
x
e
(
)
1+
λ−λ−
−=
′
ii
xx
i
eenn
0 10 40 1 0,522 48
10 20 30 0,522 0,273 25
20 30 20 0,273 0,142 13
30 40 6 0,142 0,074 7
40 50 4 0,074 0,0039 7
Обчислення спостережуваного значення критерію
2
сп
χ наведено в
таблиці:
n
i
np
i
n
i
– np
i
(n
i
– np
i
)
2
i
ii
np
npn
2
)( −
40 48 –8 64 1,33
30 25 5 25 1
20 13 7 49 3,77
6 7 – 1 1 0,14
4 7 – 3 9 1,29
53,7
)(
2
2
cп
=
−
=χ
∑
i
ii
np
npn
.
За таблицею (додаток 8) знаходимо значення критичної точки
3,11)3;01,0()3115;01,0(
2
кр
2
кр
=χ==−−==αχ k
.
Критичну область зображено на рис. 146.

138
()
2
1
2
2
2
2
2
2
2
Г2
1
)(
χ
−
−
χ
⎟
⎠
⎞
⎜
⎝
⎛
⋅
=χ e
k
f
k
k
χ
2
2
кр
χ
= 11,3
0
Рис. 146
Висновок. Оскільки
[
]
3,11;0
2
cп
∈χ
, нульова гіпотеза
про експоненціальний закон розподілу ознаки Х
приймається.
Теоретичні запитання до теми
?
1.
Дати визначення нульової та альтернативної гіпотез.
2.
Які гіпотези називають параметричними?
3.
Які гіпотези називають непараметричними?
4.
Що називають простою та складною статистичними гіпо-
тезами?
5.
Що називається статистичним критерієм?
6.
Що називається емпіричним значенням критерію?
7.
Область прийняття нульової гіпотези, критична область,
критична точка.
8.
Які Ви знаєте критичні області?
9.
Загальна методика перевірки правильності нульової гі-
потези.
10.
Що таке рівень значущості α?
11.
Помилки першого та другого роду.
12.
Що таке потужність критерію?
13.
Перевірка правильності
axH
=
Г
:
0
, при альтернатив-
них гіпотезах
axaxaxH
≠
>
<
α
ГГГ
;;:
.
14.
Який закон розподілу має випадкова величина
)(
B
B
x
ax
z
σ
−
=
?
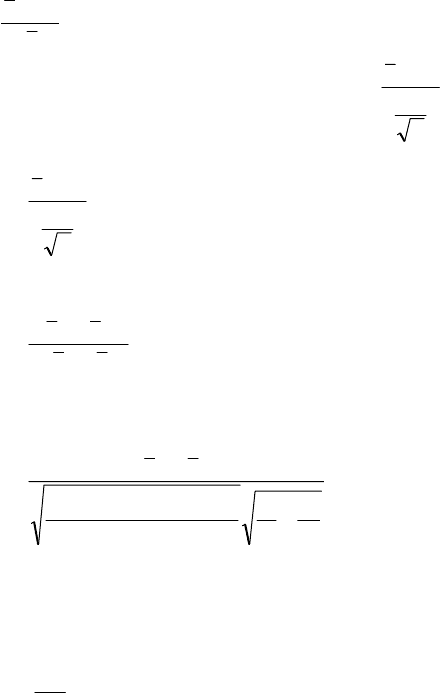
139
15.
Знаходження критичних точок для статистичного кри-
терію
)(
B
B
x
ax
z
σ
−
=
.
16.
Коли застосовується статистичний критерій
n
S
ax
z
−
=
B
?
17.
Який закон розподілу ймовірностей має статистичний
критерій
n
S
ax
z
−
=
B
?
18.
Перевірка правильності
)()(:
0
YMXMH
=
при
40>n
.
19.
Який закон розподілу ймовірностей має статистичний
критерій
)(
BB
BB
yx
yx
z
−σ
−
=
?
20.
Який статистичний критерій застосовується для переві-
рки правдивості
)()(:
0
YMXMH
=
, якщо
40
<
n
?
21.
Який закон розподілу ймовірностей має статистичний
критерій
nnnn
SnSn
yx
z
yx
′′
+
′
−
′′
+
′
−
′′
+−
′
−
=
11
2
)1()1(
22
BB
?
22.
Перевірка правильності
yx
DDH
=
:
0
.
23.
Який статистичний критерій вибирається для перевірки
правильності
yx
DDH
=
:
0
?
24.
Який закон розподілу ймовірностей має статистичний
критерій
2
2
M
S
S
F
δ
=
?
25.
Які існують підстави для висунення гіпотези про закон
розподілу ознаки генеральної сукупності?
26.
Що називають емпіричними частотами?
27.
Що називають теоретичними частотами?
28.
Записати формулу для теоретичної частоти, якщо при-
пускається, що ознака Х має пуассонівський закон розподілу
ймовірностей.
29.
Записати формулу для обчислення теоретичних частот,
якщо припускається, що ознака Х генеральної сукупності
має експоненціальний закон розподілу.

140
30.
Записати формули для обчислення теоретичних частот,
якщо припускається, що ознака Х генеральної сукупності
має нормальний закон розподілу.
31.
Критерій узгодженості Пірсона.
32.
Загальна методика перевірки правильності Н
0
про закон
розподілу ознаки генеральної сукупності.
Задачі до теми
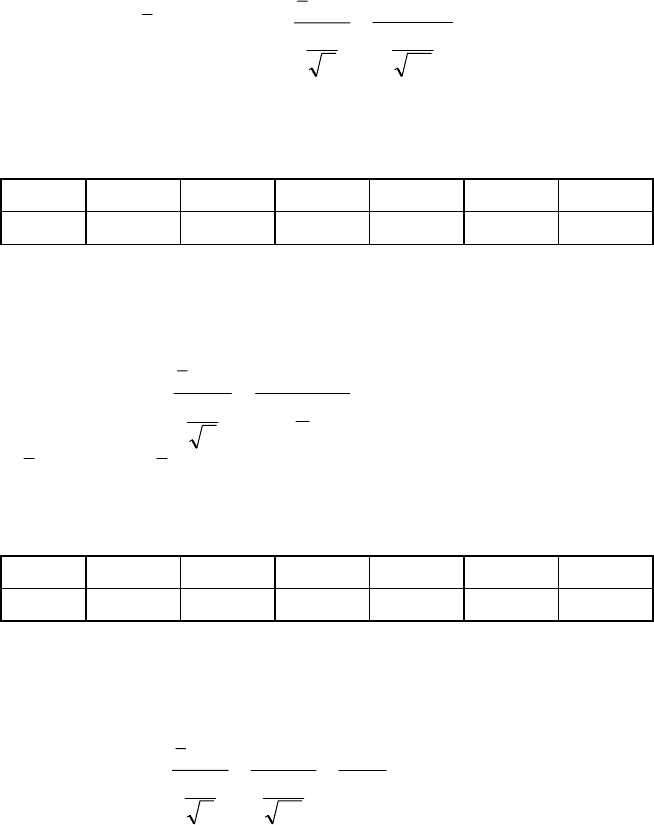
1. За заданим статистичним розподілом вибірки, реалізованим із ге-
неральної сукупності, ознака Х якої має нормальний закон розподілу
x
i
4,2 6,2 8,2 10,2 12,2
n
i
6 8 12 8 2
140
при рівні значущості α = 0,01 перевірити правильність нульової гі-
потези
10)(:
0
=XMH
, якщо альтернативна гіпотеза
10)(: >
α
XMH
, якщо
4
=
σ
r
.
Відповідь.
78,7=
B
x
; 33,3
36
4
1078,7
−=
−
=
σ
−
=
∗
n
ax
z
r
B
; 32,2
р
=
к
z .
]]
32,2;∞−∈
∗
z
; 10)(:
0
=
XMH приймається.
2. Проведено 25 незалежних вимірювань випадкової величини Х, що
має нормальний закон розподілу зі значенням
Г
σ
= 2:
x
i
2,4 5,4 8,4 11,4 14,4 17,4
n
i
2 3 10 6 3 1
При рівні значущості α = 0,001 перевірити правильність нульової
гіпотези
5,10)(:
0
=XMH , якщо альтернативна гіпотеза
5,10)(:
0
<XMH .
Відповідь.
95,3
5
2
5,1092,8
−=
−
=
σ
−
=
∗
n
ax
z
r
B
; 3
р
−
=
к
z .
]]
3;
*
−∞−∈z ,
[
[
∞−∈ ;3
*
z ; 5,10)(:
0
=
XMH приймається.
3. Маємо дані про розподіл підприємств певної області за зростан-
ням виробітку на одного працівника у відсотках до наступного року:
x
i
, % 75 85 95 105 115 125
N
i
5 8 10 5 2 1
Ураховуючи, що ознака має нормальний закон розподілу зі значен-
ням σ
Г
= 6, перевірити правильність нульової гіпотези при α = 0,01.
90)(:
0
=XMH , якщо альтернативна гіпотеза
90)(: ≠
α
XMH .
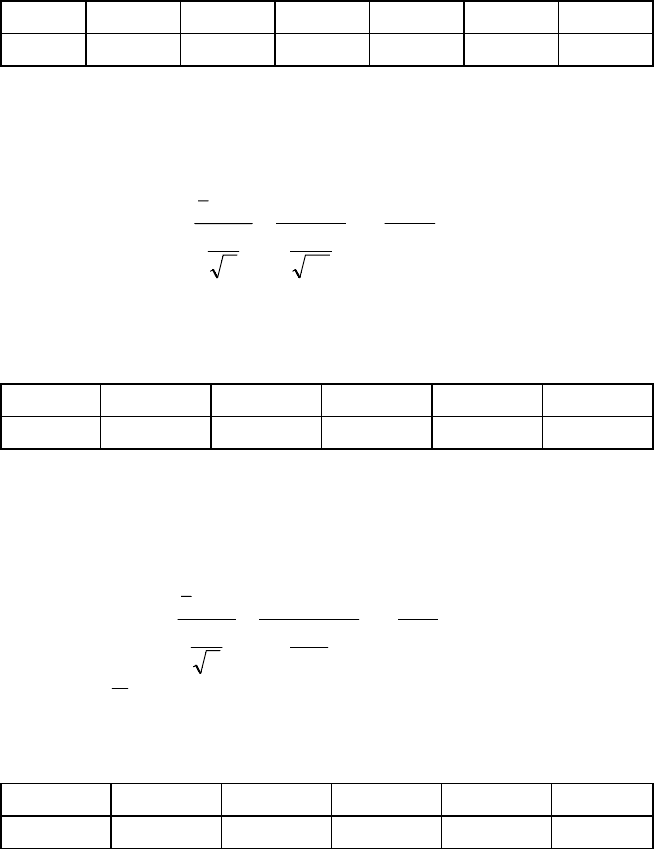
Відповідь.
48,5
095,1
6
30
6
9096
==
−
=
σ
−
=
∗
n
ax
z
Г
B
; 32,2
−
=
′
кp
z ;
32,2=
′′
кp
z ;
[]
32,2;32,2−∈
∗
z гіпотеза 90)(:
0
=
XMH приймається.
141
4. У результаті двадцяти незалежних вимірювань певної величини Х
дістали статистичний розподіл:
x
i
3,4 6,4 9,4 12,4 15,4 18,4
n
i
2 4 8 3 2 1
Припускаючи, що випадкова величина Х має нормальний закон роз-
поділу, при рівні значущості α = 0,01 перевірити правильність
10)(:
0
=XMH
, якщо альтернативна гіпотеза
10)(: >
α
XMH .
Відповідь.
346,0
868,0
3,0
20
88,3
107,9
−=−=
−
=
−
=
∗
n
S
ax
t
B
; .09,2
р
=
к
t
]09,2;]
*
∞−∈t ;
10)(:
0
=
XMH
приймається.
5. Результати вимірювання зросту дівчаток віком 16 років дали такі
показники:
h = 4, см 160—164 164—168 168—172 172—176 176—180
n
i
4 6 20 4 2
Вважаючи, що випадкова величина Х — зріст дівчаток — має нор-
мальний закон розподілу, при рівні значущості α = 0,001 перевірити
правильність нульової гіпотези
180)(:
0
=XMH , якщо альтернативна гіпотеза
180)(: ≠
α
XMH .
Відповідь.
42,12
86,0
7,10
6
17,5
1803,169
−=−=
−
=
−
=
∗
n
S
ax
t
B
; 65,3−=
′
кp
t ;
65,3=
′′
кp
t
[]
65,3;65,3−∈
∗
t
; 180)(:
0
=
XMH відхиляється.
6. Рівноточні вимірювання довжини двадцяти однотипних деталей
дали такі результати:
x
i
, мм 122,8 128,8 134,8 140,8 146,8
n
i
2 6 8 3 1
Вважаючи, що випадкова величина Х — довжина деталі — має но-
рмальний закон розподілу, при рівні значущості α = 0,001 перевірити
правильність нульової гіпотези
