Живоглядов В.Г. Теория движения транспортных и пешеходных потоков

Подождите немного. Документ загружается.

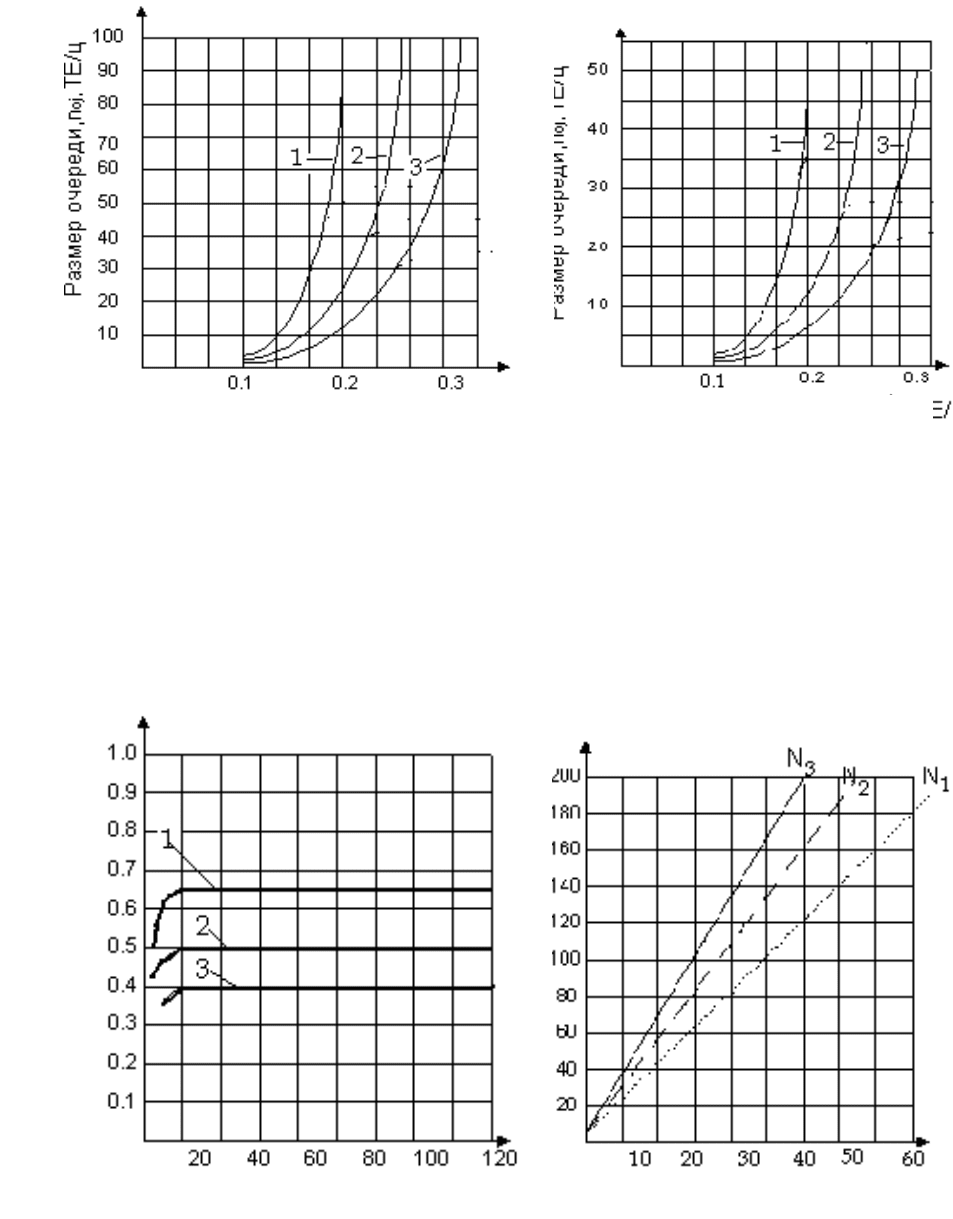
Размер очереди n

, ТЕ/цикл

Рис. 6.16. Зависимость размера

очереди от λ

и τ

(табл. 6.9–6.11):

1 – n

при τ

=2,5 с/ТЕ;

2 – n

при τ

=2,0 с/ТЕ;

3 – n

при τ

=1,5 с/ТЕ

Интенсивность прибытия



, ТЕ/с

Размер очереди n

, ТЕ/цикл

Интенсивность прибытия 

, ТЕ/с

Рис. 6.17. Зависимость t

от λ

(табл.

6.9–6.11):

1 – n

при τ

=2,5 с/ТЕ;

2 – n

при τ

=2,0 с/ТЕ;

3 – n

при τ

=1,5 с/ТЕ

Интенсивность пропуска

) при t

зелj

Размер очереди ТС n

, ТЕ/цикл

Длительность разрешающего такта t

зелj

, с Длительность циклов СР, С, с

Рис. 6.18. Зависимость (n

)

от t

зелj

(табл. 6.9–6.11):

1 – (n

) при τ

=1,5 с/ТЕ;

2 – (n

) при τ

=2,0 с/ТЕ;

3 – (n

)

при τ

=2,5 с/ТЕ

Рис. 6.19. Динамика размеров оче-

редей ТС при оптимальных длитель-

ностях циклов

(табл. 6.9–6.11):

– n

при τ

=2,5 с/ТЕ

– n

при τ

=2,0 с/ТЕ;

– n

при τ

=1,5 с/ТЕ;

200

180

160

140

120

100

611

Зависимость длительности циклов светофора С (cм. рис. 6.14) и разре-

шающих тактов (см. рис. 6.15, табл. 6.9–6.11) от интенсивности прибытия ТС

к стоп – линии носит параболический вид. Максимумы длительности цик-

лов СР (С) и разрешающих тактов (t

зелj

) наступают тем раньше, чем больше

временной интервал τ

(см. рис. 6.14 и 6.15, табл. 6.9–6.11).

По каждой принятой длительности цикла С определяются его основные

такты 

(С – Т

), 

(С – Т

), параметры и значения которых n

, t

, n

, Z

hcj

показаны: по группам перекрестков, в частности по группе “C”(С

, С

). Прямая линия MN

(см. рис. 6.19, табл. 6.11) характеризует динамику

размеров образовавшейся очереди ТЕ при постоянной величине 

=2, 5с/ТЕ,

при =0, 1 - 0, 18, с кратностью 0, 02 ТЕ/с за цикл светофора. Эта прямая

, под углом  = 1119 tgα = 1/5 =0, 2 есть график линейной функции у =

0,2х – 1,6.

Размер очереди перед перекрестком также определяется через эту ли-

нейную функцию:

Проверка при цикле 20 с : 

=2, 5с/ТЕ,

у = 0,220 – 1,6 = 2,4 ТЕ/ц ; у = n

= 2,4; (6.28)

0,2

k tg

  

– угловой коэффициент прямой MN

;  = 1119.

Здесь k = tgy и размер очереди у стоп-линии n

0jk

обратно пропорцио-

нальны временному интервалу между передними бамперами ТС (τ

По табличным данным (cм. табл. 6.9 и 6.10) построенный график (см.

рис. 6.19), на котором прямые линии MN

и MN

, характеризующие соответ-

ственно при 

=2с/ТЕ и 

=1, 5с/ТЕ размеры очередей у стоп-линии n

и при

изменяющихся длительностях циклов СР, приближен к линейной зависимо-

сти:

при 

=2с/ТЕ у = 0, 25х – 2; k = tg = 0, 25;  = 142; (6.29)

при 

=1,5с/ТЕ у = 0,333х – 2,665; k = tg = 0,333;  = 1825. (6.30)

612

Здесь k = tg,  и размеры очередей у стоп-линии СО обратно пропор-

циональны 

jк

и прямо пропорциональны длительности циклов С и интенсив-

ности прибытия ТС к перекрестку λ

jк

. При этом количество не пропущенных

ТЕ всегда следует считать отрицательным числом.

Ординаты, заключенные в прямоугольном треугольнике Оt

(см. рис.

6.1), характеризуют размер дополнительной очереди ТС, которая сможет

проходить за время, оставшееся от пропуска основной очереди при разре-

шающем такте t

зел

Количество ТЕ дополнительной очереди определяется по

= (t

– t

)/

, при этом число получается всегда положительное (см. рис.

6.1). Так, если разность равна 0, т.е. n

0max

– n

= 0, а значит n

0max

= n

, то пере-

кресток работает нормально, без заторов и с максимальным использованием

его потенциала.

Разность, равная нулю, соответствует пересечению прямых t

и t

точке О. Между перпендикулярами О

и О

заключена область, при ко-

торой перекресток работает нормально с минимальными задержками. Точки

и О

соответствуют длительности циклов С, равных 55 и 63 соответствен-

но. Длительность цикла С, полученная расчетным путем, находится в облас-

ти между О

и О

. Область, заключенная между началом координат и

точками О

и О

, несомненно соответствует положению на грани затора, но

за ее пределами, правее О

заторы не возникнут, но имеет место снижение

эффективности использования разрешающего такта.

При исследовании аналогичным методом динамики длительности цик-

ла С на втором перекрестке (группа “A”, табл. 6.1, рис. 6.2) получим, что

прямые MN, M

характеризуются линейными функциями:

MN = n

= 0,172x + 1,72; tg = 0,172;  = 932,

= С

= 0,2x; tg = 0, 2;  = 1119.

Ординаты, заключенные между прямыми МО и М

(см. рис. 6.2), иллюстрируют то количество ТЕ, которое не будет пропущено

613

через перекресток при зеленом сигнале. Это же подтверждается ординатами,

заключенными между прямой М

и кривой О

. Область, заключенная

между О

и О, является оптимальной как в отношении пропускной способно-

сти, так и задержек. В этой же области находится расчетная, наиболее выгод-

ная длительность цикла светофора С = 55 – 74 с, причем С соответствует ус-

ловиям равенства

t T

q r





 

Уравнения прямых исследуемых параметров

зел

, t

, Z

1ТЕ

, Cλ

jк

, n

с результатами их расчетов сведены в табл. 6.12.

Таблица 6.12

Уравнения прямых линий исследуемых параметров с результатами

их расчетов (сравнительная)

№ таблиц

нтенсивность

пр

ибытия 

, ТЕ/с

№ колонок та

блиц

№

рисунков

Исследуемая

прямая

согласно

рисунку

№ выведе

нного

уравнения пр

ямой

Выведенное

уравнение

tg



6.1 0,2 8 и 6 6.1 t

6.1 у=0,5х-4 0,5





6.1 0,2 14 и 6 6.1 t

6.2 у=0,369х+4,339 0,369





6.1 0,2 16 и 6 6.1 Z

1ТЕ

6.3 у=0,25х+3 0,25





6.1 0,2 11 и 6 6.2 MN(n

) 6.4 у=0,172х+1,72 0,172





6.1 0,2 10 и 6 6.2



)

6.5 у=0,2х 0,2





6.3 0,1 14 и 7 6.3 M

) 6.6 у=0,0885х+1,0544

0,0885





6.3 0,1 16 и 7 6.3 Z

1ТЕ

) 6.7 у=0,25х+3 0,25





6.3 0,1 8 и 7 6.3 t

зелj

) 6.8 у=0,5х-4 0,5





6.4 0,24 14 и 7 6.3 M

) 6.9 у=0,4616х+5,53 0,4616





6.4 0,24 16 и 7 6.3 Z

1ТЕ

) 6.10

=0,25

(до 20 с

были заторы)

0,25

142

6.4 0,24 8 и 7 6.3 t

зелj

) 6.11

у=0,5х-4 0,5





6.5 0,1-1,32

10, 7 и 4 6.8

при 

=1,5)

6.12

у=0,333х-3,33 0,333

1825

6.6 0,1-0,24

10, 7 и 4 6.8

при 

=2)

6.13

у=0,2499х+2,49 0,2499

142

6.7 0,1-0,18

10, 7 и 4 6.8

при 

=2,5)

6.14

у=0,2х-2 0,2

1119

6.8 0,1-0,16

10, 7 и 4 6.8

при



=3)

6.15

у=0,166х-1,666 0,166





6.11

0,1-0,18

10, 7 и 4 6.19

при 

=2,5)

6.16

у=0,2х-1,6 0,2

1119

6.10

0,1-0,24

10, 7 и 4 6.19

при 

=2)

6.17

у=0,25х-2 0,25

142

6.9 0,1-0,32

10, 7 и 4 6.19

при 

=1,5)

6.18

у=0,333х-2,665 0,333

1825

614

Продолжение таблицы 6.12

6.5 0,1-0,32

15.1, 7 и 4

6.10, 6.22

1ТЕ

при 

=1,5)

6.16

у=0,25х+3 0,25

142

6.6 0,1-0,24

15.1, 7 и 4

6.10, 6.22

1ТЕ

при 

=2)

6.17

у=0,25х+3 0,25

142

6.7 0,1-0,18

15.1, 7 и 4

6.10, 6.22

1ТЕ

при 

=2,5)

6.18

у=0,25х+3 0,25

142

6.8 0,1-0,16

15.1, 7 и 4

6.10, 6.22

1ТЕ

при 

=3)

6.19

у=0,25х+3 0,25

142

6.5 0,1-0,32

15.2, 7, и 4

6.10

1ТЕ

при 

=1,5)

6.20

у=0,5х 0,5

2634

6.6 0,1-0,24

15.2, 7 и 4

6.10

1ТЕ

при 

=2)

6.20

у=0,5х 0,5

2634

6.7 0,1-0,18

15.2, 7 и 4

6.10

1ТЕ

при 

=2,5)

6.20

у=0,5х 0,5

2634

6.8 0,1-0,16

15.2, 7 и 4

6.10

1ТЕ

при 

=3)

6.20

у=0,5х 0,5

2634

Прямые линии NN

(

= 1, 5 с/ТЕ), NN

(

= 2), NN

(

= 2, 5), NN

(

= 3),

характеризующие динамику очередей n

(см. рис. 6.8), имеют tg в десять раз

меньше в – отрезков на ординате. С увеличением временного интервала 

1, 5; 2; 2, 5; 3 с/ТЕ соответственно уменьшается tg на 33; 24, 9; и 20, 5% (см.

табл. 6.12).

Прямые линии MN

(

= 1,5), MN

(

= 2), MN

(

= 2,5), характери-

зующие динамику очередей ТС n

(см. рис. 6.19), имеют tg в восемь раз

меньше в – отрезков на ординате. Здесь уменьшилась величина в в связи с

уменьшением суммарной длительности желтых сигналов Т

с 8 до 6 с. С уве-

личением 

jк

уменьшается tg,  и в

(табл. 6.12, рис. 6.20). Таким образом,

чем плотнее ТП, значит меньше 

больше tg, угол . Размер очереди за-

висит от интенсивности прибытия ТС к

стоп-линии λ

jк

, а значит и от временного

интервала между передними бамперами

ТС



, а также от длительности цикла

С. Рассасывание очередей зависит от

временного интервала между передни-

0,2

0,1

2 3

0,3

0,4



Временной интервал



Рис. 6.20. Зависимость

от τ

(см. табл. 6.12)

615

ми бамперами ТС при пересечении ими стоп-линии



, т.е. от интенсивно-

сти пропуска потоков через перекресток. Чем меньше 

при пересечении

стоп-линии, тем больше интенсивность пропуска потоков и больше коэффи-

циент эффективности использования разрешающего такта, т.е. здесь присут-

ствует обратно – пропорциональная зависимость.

Прямые линии Z

1ТЕ

(см. рис. 6.1, табл. 6.1), Z

(см.

рис. 6.3, табл. 6.3), Z

(см. рис. 6.3, табл. 6.4), ZZ

(см. рис. 6.10, табл. 6.5 –

6.8), ZZ

(см. рис. 6.10, табл. 6.5 – 6.8), характеризующие динамику задержек

ТС у стоп-линий СО, имеют вид tg  по методу профессора А.А. Полякова 0,

25,  142 по методу автора монографии 0, 5,  2634. Механизм возникно-

вения суммарных задержек ТС, адекватен механизму образования очередей

ТС. Как задержки ТС, так и очереди ТС образуются при запрещающих дви-

жение тактах СР и интервале между включением зеленого сигнала и началом

движения последнего автомобиля очереди, что по сути присутствует в мето-

де автора монографии. Динамика задержек по методу профессора А.А. Поля-

кова ZZ

и [82] ZZ

иллюстрируется на рис. 6.21. По исходным данным (табл.

6.9 - 6.11) приведены формулы (6.16) – (6.19). Построена прямая линия Z

1ТЕ

совпадающая с теоретической – эмпирической (рис. 6.22).

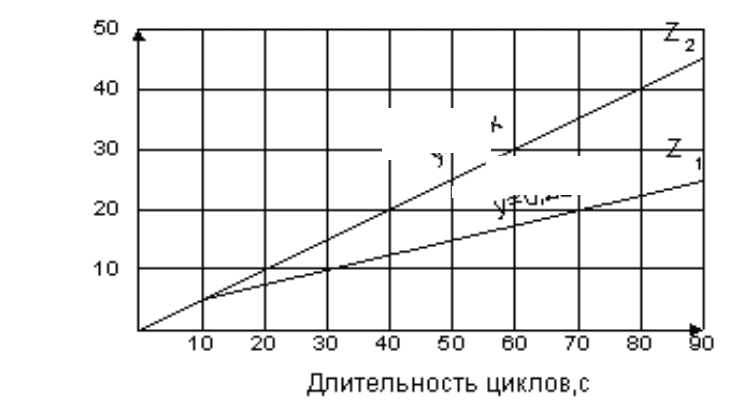
Рис. 6.21. Динамика задержек (табл. 6.12):

– по методу А.А. Полякова;

– по методу [82]

Задержки y=z, с/ТЕ

y = 0,5x

y = 0,25x+3

616

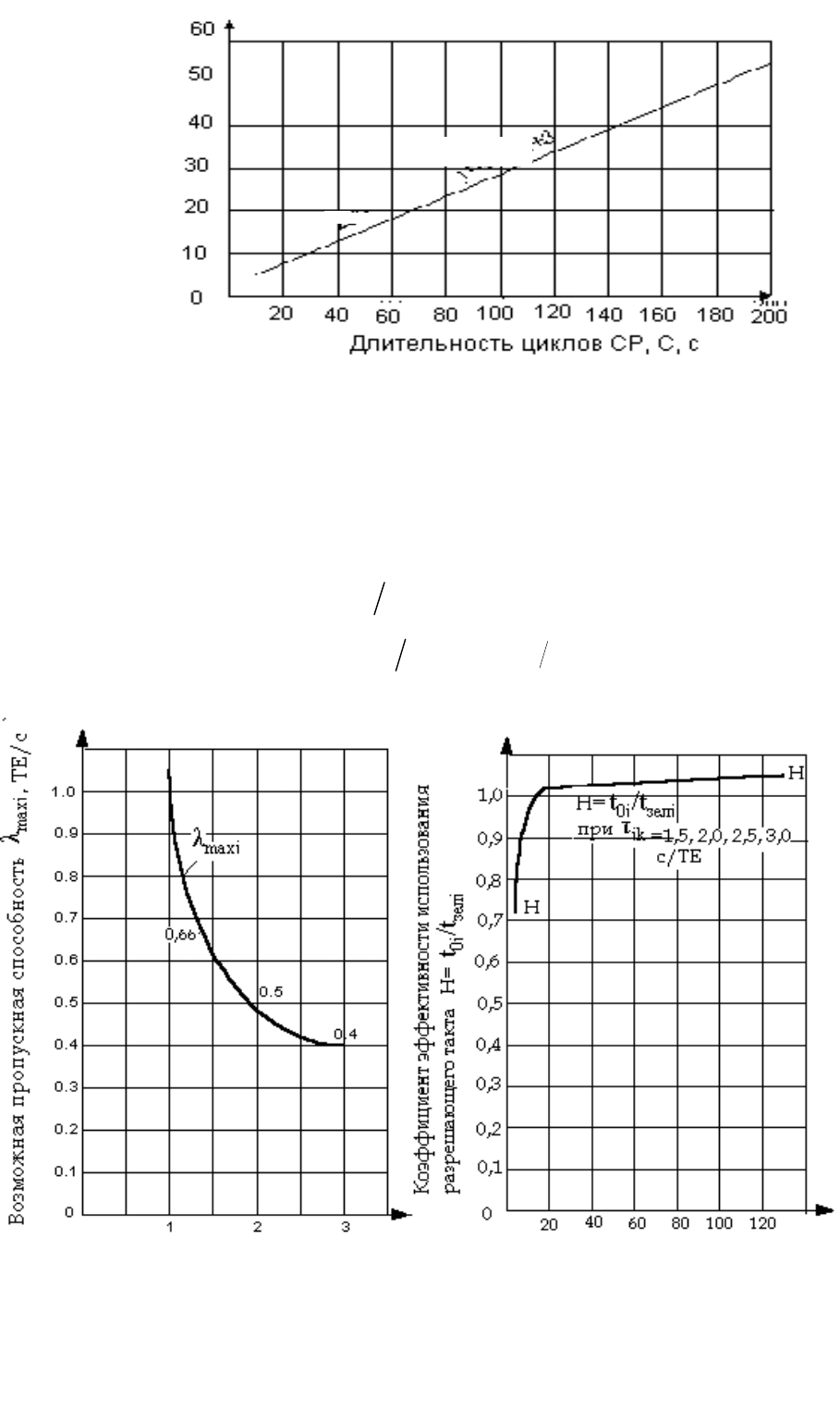
Рис. 6.22. Зависимость задержек одной ТЕ

от длительности циклов СР (табл. 6.9 – 6.11)

На рис. 6.23 представлена часть ветви гиперболы, характеризующей за-

висимость возможной пропускной способности 

maxjk

от временного интерва-

ла 

. Данная ветвь описывается уравнением





1 0,25 0,75 .

y x

 

Проверка: х=2 с/ТЕ, тогда





1 0,25 1,5 11,75 0,57

   

, 0,50,57. Погреш-

ностью 0,07 можно пренебречь.

Временной интервал 

, с/ТЕ

Длительность разрешающего

такта t

зелi

, с

Рис. 6.23. Зависимость λ

maxj

от τ

(табл. 6.9 – 6.11)

Рис. 6.24. Динамика коэффициента эф-

фективности использования

разрешающего такта

(табл. 6.9 – 6.11)

Задержки одной ТЕ Z

1ТЕ

, с/ТЕ

y = 0,25x+3

617

Размер очереди определяется по формуле (2. 160), при этом всегда полу-

чается положительное число. Если n

max-oj

omax

–n

=0, то перекресток функ-

ционирует нормально, без заторов и с максимальной эффективностью ис-

пользования его потенциала. Это подтверждается данными, полученными

графическими (рис. 6.2) и аналитическими методами, результаты которых

сведены в табл. 6.1. Так, разность, равная нулю, соответствует пересечению

прямых MN и M

в точке О и кривой О

с прямой линией М

. Длитель-

ность цикла в точке О, равная 58 с, является такой длительностью, при кото-

рой перекресток функционирует нормально и в то же время с наименьшими

издержками, но на грани возможных заторовых состояний. Это можно заме-

тить при исследовании динамики длительности цикла С на перекрестках

группы «С» (см. рис. 6.14 – 6.18, табл. 6.9 – 6.11) аналогичным методом. Дру-

гие длительности циклов С, когда они больше или меньше временных разме-

ров ТП, имеют отрицательные характеристики (или превышенные задержки,

или заторы).

Можно сделать вывод, что наиболее выгодной и оптимальной длитель-

ностью цикла С считается только та длительность, которая отвечает требова-

ниям равенства

T nt

l q r





 

. Если

T nt

l q r





 

или С>

T nt

l q r



 

будут заторы

или максимальные задержки соответственно, что не отвечает требованиям

оптимального пропуска ТПП.

6.4. Исследования зависимости оптимальности цикла от размеров основных

параметров потока и перекрестков

Каждой оптимальной С в зависимости от размеров ТП λ

и динамиче-

ских качеств ТС, геометрии перекрестка Т

, временного интервала между

передними бамперами ТС при проезде стоп-линии τ

, интервала между

включением зеленого сигнала и троганием с места первой ТЕ t

и всей оче-

реди t

, а также от количества фаз n в цикле соответствует своя, только ей

присущая пропускная способность перекрестка. Когда сумма динамических

618

характеристик q+r стремится к единице, но не равна ей, то пропускная спо-

собность перекрестка достигает максимума и С становится бесконечно

большой. Но q+r может расти только до известного предела

C T nt

 

т.е. q+r

C T nt

 

 .В противном случае n

omaxj

, α

(С–Т

)<t

, т.е. воз-

никнут заторы в движении, даже если цикл станет бесконечно большим. Чем

больше зона перекрестка, тем больше Т

и тем раньше наступает бесконечно

большая длительность цикла С. А когда выражение q+r стремится к 0, но не

равно ему, пропускная способность перекрестка используется минимально, а

С стремится к





+…..+

Отметим, что С=Т

только тогда, когда q+r = 0. Рассмотрим влияние

каждого параметра на величину и диапазон циклов, а также на их оптималь-

ность.

Для исследования зависимости С от λ

приняты перекрестки «А», «В»,

«С» и выполнены расчеты оптимальных длительностей циклов С и его тактов

зел.

, t

кр.



по исходным параметрам λ

= 0, 1÷0, 32 TE/c, τ

= 1, 5;2; 2, 5; 3

с/ТЕ, Т

=3 и 4с. Помимо оптимальной С для каждой величены λ

приняты

увеличенные С. По полученным оптимальным и увеличенным длительностям

циклов С выполнены расчеты основных тактов по формулам (2.9) – (2.67)

главы 2.

Для простоты расчета и анализа полагаем, что α

и β

в режимах регули-

рования между собой равны, т.е. α

= β

=0, 5. Размеры очереди n

, продолжи-

тельность ее пропуска через перекресток при разрешающем такте t

и другие

параметры такие, как n

, t

, Z

определены по формулам (2.160 –

2.218) главы 2, результаты которых помещены в табл. 6.1-6.12 и отражены на

графиках (см. рис. 6.1 - 6.24). Кривые ОС

, ОС

(см. рис. 6.14) характе-

619

ризуют зависимость оптимальных длительностей циклов С, размеров пара-

метров ТП λ

и τ

=1,5; 2,0; 2,5 с/ТЕ соответственно. Линии A

(см. рис. 6.25,

табл. 6.1 и 6.3) характеризуют зависимость увеличенных по отношению к оп-

тимальным С при тех же λ

и τ

. По расчетным данным таблиц и построенным

по этим данным линиям видно, что с увеличением интенсивности λ

прогрес-

сивно растет длительность цикла С, а при увеличении τ

с 1 до 2 с/ТЕ пропу-

скная способность перекрестка дорог сокращается по сравнению с τ

= 1 с/ТЕ

на 70 %. Длительность цикла С при этом достигает больших величин. Следу-

ет отметить, что длительность цикла светофора С при λ

jк

>0, 24 ТЕ/с стремит-

ся к бесконечно большой величине.

Зависимость длительности цикла С от значений λ

и τ

со всей очевид-

ностью показана кривыми (на рис. 6.5 и 6.28, (см. табл. 6.5 – 6.8).

Кроме того, с ростом λ

, τ

и С соответственно увеличиваются и другие

параметры: размеры очередей перед перекрестками, задержки как одной ТЕ,

так и всей очереди за цикл или в единицу времени. Особенно это заметно на

неоптимальных длительностях циклов светофора С (см. табл. 6.1–6.4). На-

сколько принятая С

больше длительности С, соответствующей условиям ра-

венства выражения

T nt

l q r





 

, на-

столько больше размеры очереди n

задержки одной ТЕ Z

ITE

и задержки

за один час «работы» перекрестка

. Разница в задержках за один час

работы светофоров на перекрестках

групп «А» «В» и «С» при оптималь-

ных циклах С в сравнении с приня-

тыми увеличенными длительностями

циклов показана в табл. 6.1 – 6.11.

Преимущество оптимального цикла

в них просматривается весьма оче-

0.1 0.2 0.3

100

150

200

250

300

оптим

увелич

Интенсивность движения, ТЕ/с

Длительность циклов, С

Рис. 6.25. Динамика зависимости С от λ (см.

табл. 6.1 и 6.3).

Длительность циклов С, с

620