Живоглядов В.Г. Теория движения транспортных и пешеходных потоков
Подождите немного. Документ загружается.


Таблица 4.1
Зависимость основных характеистик РКД от интенсивности прибытия транспортных средств к стоп-линим примыканий.
N
λ
1
j
λ
2
j
λ
3
j
λ
4
j
λ
j
λ
r
2
j
1
λ
r
1
j
2
λ
r
3,4
j
3
T
1
j
T
2
j
T
3,4
j
h
1
j
h
2
j
h
3
j
h
4
j
R
j
1
t
0
j
1
1
0,033
0,033
0,017
0,017
0,1
0,033
0,067
0,1167
3
2
4
0,0328
0,0328
0,0165
0,0165
0,0986
3,0418
2
0,038
0,038
0,019
0,019
0,115
0,038
0,077
0,1342
3
2
4
0,0376
0,0376
0,019
0,019
0,1132
3,0481
3
0,043
0,043
0,022
0,022
0,13
0,043
0,087
0,1517
3
2
4
0,0424
0,0424
0,0214
0,0214
0,1277
3,0544
4
0,048
0,048
0,024
0,024
0,145
0,048
0,097
0,1692
3
2
4
0,0472
0,0472
0,0239
0,0239
0,1421
3,0608
5
0,053
0,053
0,027
0,027
0,16
0,053
0,107
0,1867
3
2
4
0,0519
0,0519
0,0263
0,0263
0,1565
3,0671
6
0,058
0,058
0,029
0,029
0,175
0,058
0,117
0,2042
3
2
4
0,0567
0,0567
0,0287
0,0287
0,1708
3,0734
7
0,063
0,063
0,032
0,032
0,19
0,063
0,127
0,2217
3
2
4
0,0614
0,0614
0,0312
0,0312
0,1851
3,0797
8
0,068
0,068
0,034
0,034
0,205
0,068
0,137
0,2392
3
2
4
0,0661
0,0661
0,0336
0,0336
0,1993
3,0861
9
0,073
0,073
0,037
0,037
0,22
0,073
0,147
0,2567
3
2
4
0,0707
0,0707
0,036
0,036
0,2134
3,0924
Продолжение таблицы 4.1
T
0
1
=T
0
2
T
0
q r С α=β
t
зел
=t
кр
n
0
j
Z
j
Z
j
1TE
t
0
j
t
x
j
n
x
j
λ
max
t
0
j
/t
зел
3,041828
6,0837
0,2
0,2
11,81
0,5
2,861
1,181
1,806094816
1,529799
2,486219
0,375
0,1875
0,121176
0,868937
3,048131
6,0963
0,23
0,23
13,14
0,5
3,522
1,511
0,195492119
0,129359
3,171832
0,350649
0,175325
0,134024
0,900454
3,05444
6,1089
0,26
0,26
14,81
0,5
4,351
1,925
6,54340975
3,398606
4,026319
0,324324
0,162162
0,14688
0,925454
3,060757
6,1215
0,29
0,29
16,96
0,5
5,417
2,459
13,22231204
5,377946
5,121461
0,295775
0,147887
0,159744
0,945401
3,06708
6,1342
0,32
0,32
19,82
0,5
6,841
3,171
21,95134028
6,923101
6,57677
0,264706
0,132353
0,172615
0,961309
3,073412
6,1468
0,35
0,35
23,82
0,5
8,838
4,169
38,14811647
9,150467
8,607191
0,230769
0,115385
0,185494
0,973889
3,07975
6,1595
0,38
0,38
29,83
0,5
11,84
5,668
68,46117589
12,07868
11,64233
0,193548
0,096774
0,19838
0,983647
3,086095
6,1722
0,41
0,41
39,85
0,5
16,84
8,168
143,1542778
17,52553
16,68411
0,152542
0,076271
0,211274
0,99094
3,092448
6,1849
0,44
0,44
59,87
0,5
26,84
13,17
364,7274015
27,68895
26,73748
0,107143
0,053571
0,224175
0,996009
431
396
0
10
20
30
40
50
60
70
0,1 0,115 0,13 0,145 0,16 0,175 0,19 0,205 0,22
Интенсивность прибытия на примыканиях, ТЕ/с
Длительность цикла светофора, с
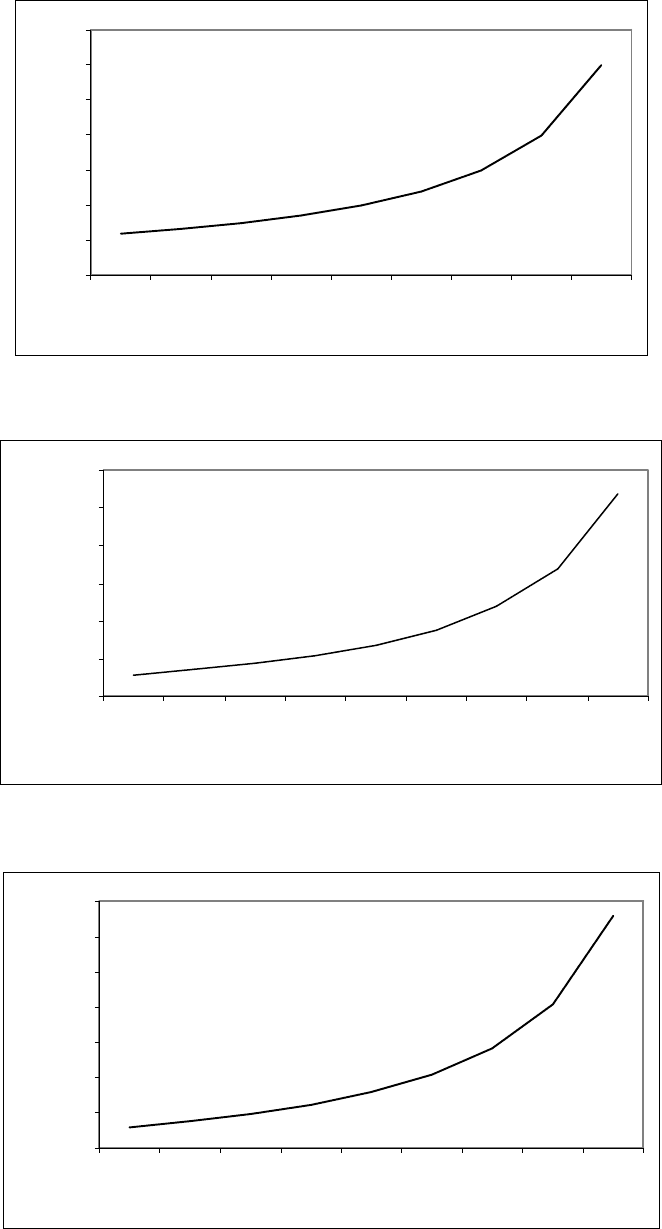
Рис. 4.14. Зависимость длительности цикла светофора С на РКД от интенсивности
прибытия транспортных средств к стоп – линиям примыканий
0
5
10
15
20
25
30
0,1 0,115 0,13 0,145 0,16 0,175 0,19 0,205 0,22
Интенсивность прибытия на примыканиях, ТЕ/с
Длительность разрешающего
такта, с
Рис. 4.15. Зависимость длительности разрешающего такта t
зел
на РКД от
интенсивности прибытия транспортных средств к стоп – линиям примыканий
0
2
4
6
8
10
12
14
0,1 0,115 0,13 0,145 0,16 0,175 0,19 0,205 0,22
Интенсивность прибытия на примыканиях, ТЕ/с
Полная очередь транспортных
средств , ТЕ
Рис. 4.16. Зависимость размера полной очереди транспортных средств n
0
на РКД от
интенсивности прибытия транспортных средств к стоп – линиям примыканий
432
397
0
50
100
150
200
250
300
350
400
0,1 0,115 0,13 0,145 0,16 0,175 0,19 0,205 0,22
Интенсивность прибытия на примыканиях, ТЕ/с
Задержка транспортных
средств , с
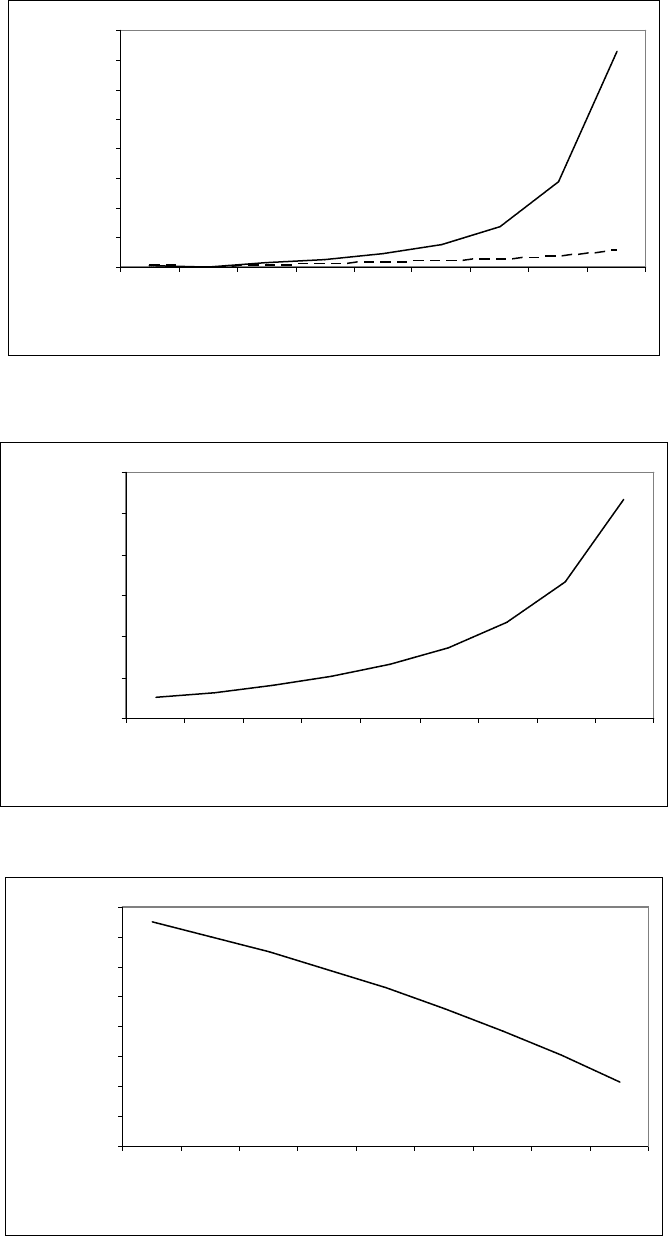
Рис. 4.17. Зависимость задержек транспортных средств Z на РКД от интенсивности
прибытия транспортных средств к стоп – линиям примыканий
0
5
10
15
20
25
30
0,1 0,115 0,13 0,145 0,16 0,175 0,19 0,205 0,22
Интенсивность прибытия на примыканиях, ТЕ/с
Время рассасывания полной
очереди транспортных средств ,
с
Рис. 4.18. Зависимость зависимость рассасывания полной очереди t
0
на РКД от
интенсивности прибытия транспортных средств к стоп – линиям примыканий
0
0,05
0,1
0,15
0,2
0,25
0,3
0,35
0,4
0,1 0,115 0,13 0,145 0,16 0,175 0,19 0,205 0,22
Интенсивность прибытия на примыканиях, ТЕ/с
Время для проезда без
остановки у стоп-линии , с
Рис. 4.19. Зависимость временного итервала для безостановочного проезда t
х
на
РКД от интенсивности прибытия транспортных средств к стоп – линиям примыканий
Z
j
Z
j1TE
433
398
0
0,02
0,04
0,06
0,08
0,1
0,12
0,14
0,16
0,18
0,2
0,1 0,115 0,13 0,145 0,16 0,175 0,19 0,205 0,22
Интенсивность прибытия на примыканиях, ТЕ/с
Количество ТС, проехавших
перкресток сходу , с
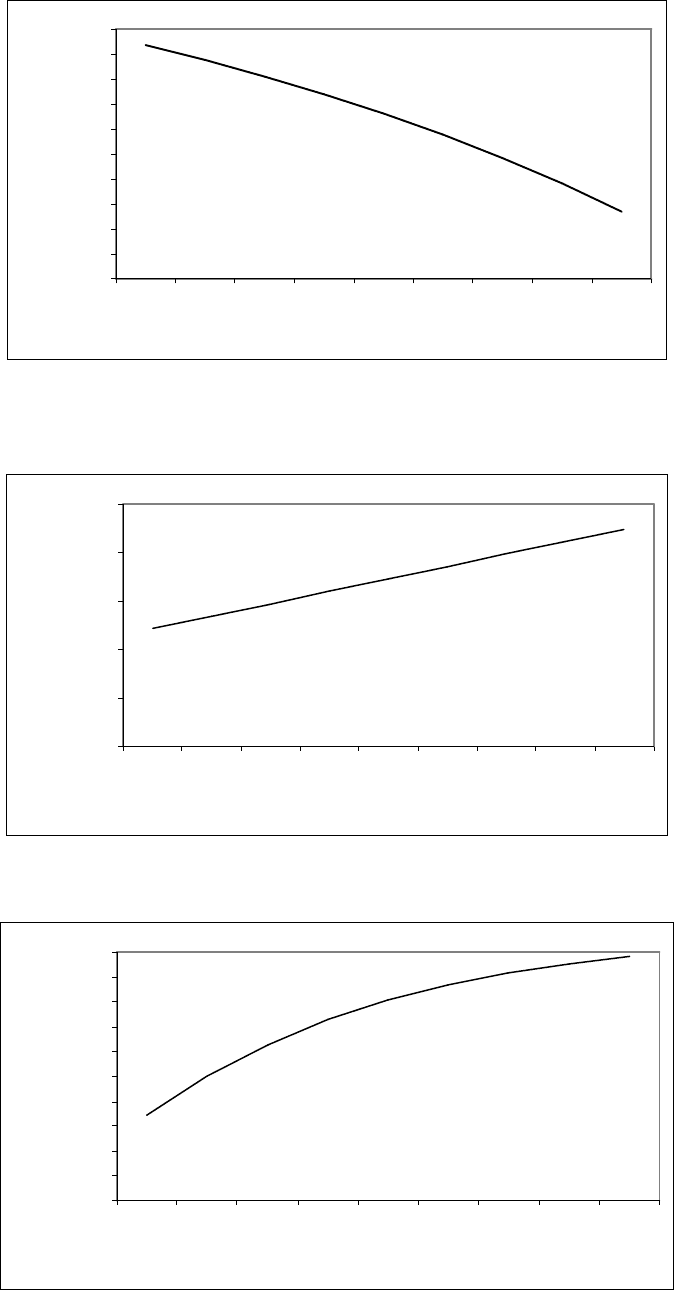
Рис. 4.20. Зависимость количества транспортных средств, прошедших перекресток
сходу n
х
на РКД от интенсивности прибытия транспортных средств к стоп – линиям
примыканий
0
0,05
0,1
0,15
0,2
0,25
0,1 0,115 0,13 0,145 0,16 0,175 0,19 0,205 0,22
Интенсивность прибытия на примыканиях, ТЕ/с
Максимальная пропускная
способность, ТЕ/с
Рис. 4.21. Зависимость максимальной пропускной способности λ
max
на РКД от
интенсивности прибытия транспортных средств к стоп – линиям примыканий
0,8
0,82
0,84
0,86
0,88
0,9
0,92
0,94
0,96
0,98
1
0,1 0,115 0,13 0,145 0,16 0,175 0,19 0,205 0,22
Интенсивность прибытия на примыканиях, ТЕ/с
Коэффициент использования
эелеого сигнала
Рис. 4.22. Зависимость коэффициента использования зеленой фазы на РКД от
интенсивности прибытия транспортных средств к стоп – линиям примыканий
434
399
4.10.4. Изучение зависимости основных характеристик работы РКД
от интенсивности движения методом апппроксимированного
моделирования
Исследование проводится на основе теоретических положений, изло-
женных в приложении к главе 2 и формул (2.258) – (2.275).
1. Изучение зависимости длительности промежуточного такта Т
0
на
РКД от интенсивности прибытия к стоп-линии примыканий. Анализ прово-
дится но основании данных таблицы 4.1 и рис. 4.12. Для правильного выбора
вида аналитической зависимости выполняются промежуточные вычисления.
На отрезке изменения переменной x, т.е. х
[0,1; 0,22] выберем точки
х
1
= 0,1 и х
n
= 0,22 наиболее удаленных друг от друга (крайние).
Вычисляется х
арм
, х
геом
, х
гарм
по формулам (2.265) и на графике геомет-
рически находятся соответствующие значения переменной у. По данным таб-
лицы (4.1) находятся у
арм
, у
геом
, у
гарм
, при этом используются формулы
(2.265) и (2.266).
x
арм
=
0,16
y
арм
=
6,134276592
y*
1
=
6,134161
x
геом
=
0,148324
y
геом
=
6,13406773
3
y*
2
=
6,124263
x
гарм
=
0,1375
y
гарм
=
6,133858881
y*
3
=
6,115167
Сравнивая числовые значения у*
1
, у*
2
, у*
3
с у
арм
, у
геом
, у
гарм
и оцени-
вая погрешности проведенных вычислений по формулам (2.267)-(2.273) по-
лучены следующие результаты:
ε
1
=|
y*
1
-y
арм
|=
0,000116
ε
5
=|
y*
2
-y
геом
|=
0,009805
ε
2
=|
y*
1
-y
геом
|=
9,33
*10
-
05
ε
6
=|
y*
3
-y
арм
|=
0,019109
ε
3
=|
y*
1
-y
гарм
|=
0,000302
ε
7
=|
y*
3
-y
гарм
|=
0,018691
ε
4
=|
y*
2
-y
арм
|=
0,010014
После этого выбирается минимальная погрешность ε из ε
i
, (i=1, 2,…7).
ε= min (ε
1
, ε
2
, ε
3
, ε
4
, ε
5
, ε
6
, ε
7
) =9,33*10
-05
Так как ε
совпадает с ε
2
, то в качестве аналитической зависимости хо-
рошим приближением служит зависимость у= аb
х
, с неизвестными парамет-
рами а и b. Для уточнения этих параметров используется метод наименьших
435
400
квадратов (МНК). Согласно этому методу значения параметров функцио-
нальной зависимости а и b следует выбрать так, чтобы сумма квадратов по-
грешностей была наименьшей (уравнение (2.274)), т.е.
F (а,b ) =
n
i
ii
baxfy
1
2
)),;((( будет минимальной, где ε
i
= у
i
– f (x
i
; a, b) – i – я
погрешность (i=1, 2,…7).
Необходимым условием существования минимума функции двух пе-
ременных является равенство нулю всех ее частных производных.
Значения параметров а и b найдем из системы уравнений (2.275). Поскольку
зависимость получилась нелинейная, то следует применять преобразование
координат к функции у=аb
х
: Прологарифмировав у=аb
х
, получили:
lg y=lg a+x*lg b, т.е. Z = A
1
t + B
1
, где Z =lg у; A
1
= lg b; B
1
= lg a; t = x.
Система уравнений (2.275) примет следующий вид: (случай линейной
зависимости):
n
i
i
n
i
i
n
i
ii
n
i
i
n
i
i
znBtA
tztBtA
1
1
1
2
1
11
1
1
2
1
или
n
i
i
n
i
i
n
i
i
n
i
i
n
i
i
ynaxb
yxaxb
11
111
2
lglglg
lglg)(lg
Далее, находятся значения а и b, путем решения системы матричным мето-
дом, предварительно осуществив расчеты, которые приведены в табл. 4.2
Таблица 4.2
Данные расчетов для МНК при определении зависимости длительности
промтакта от интенсивности прибытия
i
x
i
y
i
lgy
i
x
i
2
x
i
lgy
i
1
0,1 6,083657 0,784164712 0,01 0,0784165
2
0,115 6,096261 0,785063562 0,013225 0,0902823
3
0,13 6,10888 0,785961585 0,0169 0,102175
4
0,145 6,121513 0,786858784 0,021025 0,1140945
5
0,16 6,134161 0,787755159 0,0256 0,1260408
6
0,175 6,146823 0,788650709 0,030625 0,1380139
7
0,19 6,1595 0,789545436 0,0361 0,1500136
8
0,205 6,172191 0,79043934 0,042025 0,1620401
9
0,22 6,184896 0,791332422 0,0484 0,1740931
∑
1,44 55,20788 7,08977171 0,2439 1,1351698
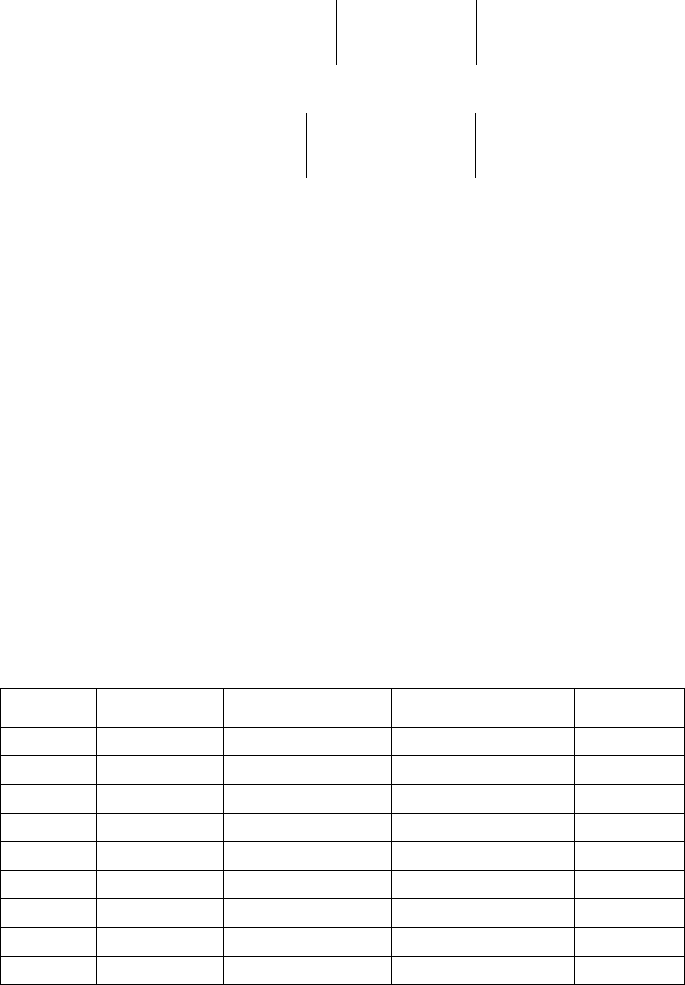
Итак, дана матрица коэффициентов при неизвестных вида:
L=
0,2439
1,44
1,44
9
436
401
а также матрица свободных членов
M=
1,1351698
7,0897717
Используя X=L
-1
M, получим
Х=
0,059730888
0,77819547
где lg a= 0,77819547, lg b= 0,059730888, отсюда a= 6,000610949, b=
1,147442385.
Эмпирическая зависимость у=аb
х
при найденных значениях a и b при-
нимает вид:
Y=1,1474424*6,0006109
X
.
Для определения точности выбора эмпирической кривой, т.е. макси-
мального отклонения табличных значений от аппроксимирующей кривой
Y=1,1474424*6,0006109
X
составим сравнительную табл. 4.3.
Таблица 4.3
Результаты отклонений табличных значений от значений, вычисленных по
эмпирической формуле Y=1,1474424*6,0006109
X
x
i
y
i
y
i
выч
γ
i
%
0,1
6,083657
6,083710772
0,0000538825
0,00
0,115
6,096261
6,096274616
0,0000134833
0,00
0,13
6,10888
6,108864407
0,0000154718
0,00
0,145
6,121513
6,121480197
0,0000329185
0,00
0,16
6,134161
6,134122041
0,0000387922
0,00
0,175
6,146823
6,146789993
0,0000330282
0,00
0,19
6,1595
6,159484105
0,0000155619
0,00
0,205
6,172191
6,172204434
0,0000136718
0,00
0,22
6,184896
6,184951031
0,0000547380
0,00
Результаты отклонений табличных значений от вычисленных по эмпи-
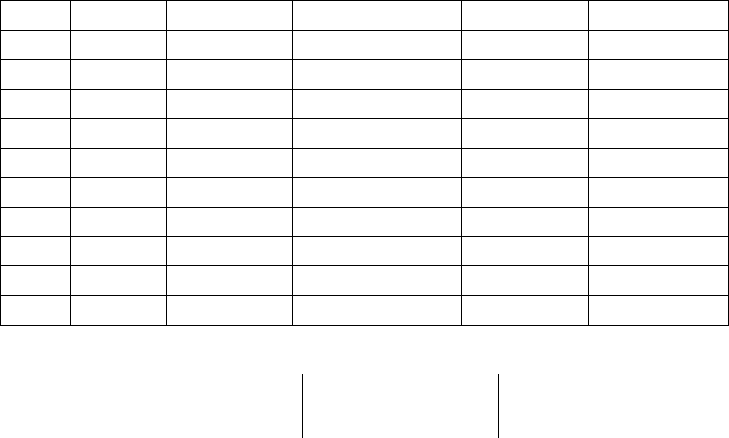
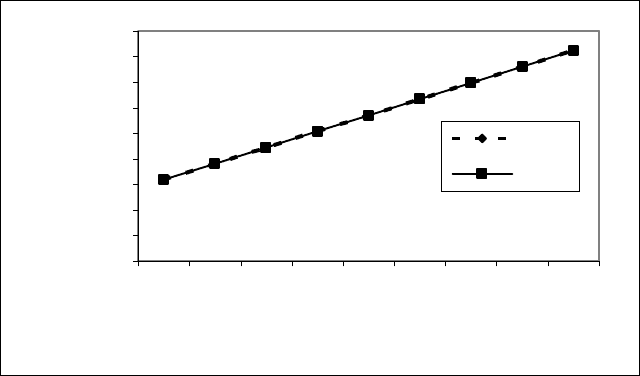
рической формуле представлены на рис. 4.23.
Таким образом, размах отклонений значений табличных от вычислен-
ных 0,0000134833÷0,0000547380, среднее взвешенное отклонение составляет
0,00%, что дает основание подтвердить точность выбранной эмпирической
кривой.
437
402
6,02
6,04
6,06
6,08
6,1
6,12
6,14
6,16
6,18
6,2
0,1
0,115
0,13
0,145
0,16
0,175
0,19
0,205
0,22
Xi
Yi,Yiвыч
Yi
Yiвыч
Рис. 4.23. Результаты отклонений табличных значений от значений, вычисленных
по эмпирической формуле Y=1,1474424*6,0006109
X
2. Изучение зависимости динамических характеристик q и r на РКД
от интенсивности прибытия транспортных средств на примыканиях. Ана-
лиз проведен на основе данных таблицы 4.1 и рис. 4.13.
По графику можно предположить, что зависимость носит линейный
характер, однако для правильного выбора вида аналитической зависимости
выполняются промежуточные вычисления. На отрезке изменения перемен-
ной x, т.е. х
[0,1; 0,22] выберем точки х
1
= 0,1 и х
n
= 0,22 наиболее удален-
ных друг от друга (крайние).
Вычисляется х
арм
, х
геом
, х
гарм
по формулам (2.265) и на графике геомет-
рически находятся соответствующие значения переменной у. По данным
табл. 4.1 находятся у
арм
, у
геом
, у
гарм
, при этом используем формулы (2.265) и
(2.266):
x
арм
= 0,16
y
арм
=
0,32
y*
1
=
0,32
x
геом
=
0,148324
y
геом
=
0,296648
y*
2
=
0,296648
x
гарм
=
0,1375
y
гарм
=
0,275
y*
3
=
0,275
Сравнивая числовые значения у*
1
, у*
2
, у*
3
с у
арм
, у
геом
, у
гарм
и оцени-
вая погрешности проведенных вычислений по формулам (2.267)-(2.273) по-
лучены следующие результаты:
ε
1
=|y*
1
-y
арм
|= 0 ε
5
=|y*
2
-y
геом
|=
0
ε
2
=|y*
1
-y
геом
|=
0,023352
ε
6
=|y*
3
-y
арм
|= 0,045
ε
3
=|y*
1
-y
гарм
|=
0,045 ε
7
=|y*
3
-y
гарм
|=
438
403
0
После этого выбирается минимальная погрешность ε из ε
i
, (i=1, 2,…7).
ε= min (ε
1
, ε
2
, ε
3
, ε
4
, ε
5
, ε
6
, ε
7
) =0
Так как ε
совпадает с ε
1
, ε
5
, ε
7
то в качестве аналитической зависимо-
сти хорошим приближением могут служить зависимости у=ах+b, у=ах
b
и
у=х/(ах+b) с неизвестными параметрами а и b, однако выберем наиболее про-
стую у=ах+b. Для уточнения этих параметров используется метод наимень-
ших квадратов (МНК). Согласно этому методу значения параметров функ-
циональной зависимости а и b следует выбрать так, чтобы сумма квадратов
погрешностей была наименьшей (уравнение (2.275)), т.е. F(а, в) =
n
i
ii
baxfy
1
2
)),;((( будет минимальной, где ε
i
= у
i
– f (x
i
; a, b) – i- я погреш-
ность (i=1, 2,…7).
Необходимым условием существования минимума функции двух пе-
ременных является равенство нулю всех ее частных производных.
Значения параметров а и b найдем из системы уравнений (2.275).
Система уравнений (2.275) примет следующий вид:
n
i
i
n
i
i
n
i
ii
n
i
i
n
i
i
ynbxa
yxxbxa
11
111
2
)(
Далее, находятся значения а и b, путем решения системы матричным ме-
тодом, предварительно осуществив расчеты, которые приведены в табл. 4.4.
Таблица 4.4
Данные расчетов для МНК при определении зависимости динамических ха-
рактеристик q и r от интенсивности прибытия
i
x
i
y
i
(x
i
)
2
x
i
y
i
1
0,1
0,2
0,01
0,02
2
0,115
0,23
0,013225
0,02645
3
0,13
0,26
0,0169
0,0338
4
0,145
0,29
0,021025
0,04205
5
0,16
0,32
0,0256
0,0512
6
0,175
0,35
0,030625
0,06125
7
0,19
0,38
0,0361
0,0722
8
0,205
0,41
0,042025
0,08405
9
0,22
0,44
0,0484
0,0968
∑
1,44
2,88
0,2439
0,4878
ε
4
=|y*
2
-y
арм
|= 0,023352
439

404
Итак, дана матрица коэффициентов при неизвестных вида:
L=
0,2439
1,44
1,44
9
а также матрица свободных членов
M=
0,4878
2,88
Используя X=L
-1
M, получим
Х=
2
0
где a= 2, b= 0, отсюда эмпирическая зависимость у=ах+b при найденных
значениях a и b принимает вид: у= 2*х.
Для определения точности выбора эмпирической кривой, т.е. макси-
мального отклонения табличных значений от аппроксимирующей прямой
у= 2*х составим сравнительную табл. 4.5.
Таблица 4.5
Результаты отклонений табличных значений от значений, вычисленных по
эмпирической формуле у= 2*х
x
i
y
i
y
i
выч
γ
i
%
0,1
0,2
0,2
7,22*10
-
16
0,00
0,115
0,23
0,23
8,05*10
-
16
0,00
0,13
0,26
0,26
9,44*10
-
16
0,00
0,145
0,29
0,29
1,05*10
-
15
0,00
0,16
0,32
0,32
1,11*10
-
15
0,00
0,175
0,35
0,35
1,22*10
-
15
0,00
0,19
0,38
0,38
1,33*10
-
15
0,00
0,205
0,41
0,41
1,44*10
-
15
0,00
0,22
0,44
0,44
1,55*10
-
15
0,00
Результаты отклонений табличных значений от вычисленных по эмпи-
рической формуле представлены на рис. 4.24.
440
