Живоглядов В.Г. Теория движения транспортных и пешеходных потоков

Каждое здесь слагаемое может быть раскрыто как в примере на k–й по-

лосе, j-го направления, h-перекрёстка (см. уравнение (2.222)).

Для того, чтобы определить размер временных задержек на одном h-

перекрестке в течение часа, следует знать количество циклов СР в одном ча-

се 3600/С, тогда:

Z

h

=





4

1j





K

K 1

(Z

jk

∙ 3600 / C

h

). (2.224)

Для того, чтобы перевести задержки из секунд в час, то следует задерж-

ки в секундах разделить на 3600.

Z

h

=





4

1j





K

K 1

(Z

jk

∙ 3600 / C

h

∙ 3600) =





4

1j





K

K 1

(Z / С).

(2.225)

Подставив значения Zjk и С получим:





K

K 1

= 1 по условию

Z

h

=





4

1i

(Z

jk

/ C

h

) = Z

11

/ C

h

+ Z

21

/ C

h

+ Z

31

/ C

h

+ Z

41

/ C

h

=

= 131 / 44 + 100 / 44 + 131 / 44 + 100 / 44 = 462 / 44 = 10,5 ч/ч

Формула определения временных размеров задержек на m-магистрали

имеет вид:

Z

m

=





H

h 1

Z

h

=





K

K 1





4

1j





H

h 1

(2





m

a 1

n

ojkam



– (a

1

+ a

m

)m



) / 2

λjk

. (2.226)

Для определения задержек ТС за один час работы всех перекрёстков m-

магистрали в часах формулу (2.226) можно представить в следующем виде:

Z

m

=





H

h 1

Z

hm

/C

hm

=





K

K 1





4

1j





H

h 1

(2





m

a 1

n

ojkam

•n

ojkam

–(a

1jkm

+ a

mjkm

)m



)/2 λ

jkmh

C

hm

.

(2.227)

Задержки на перекрестках всех магистралей дорожной сети населенного

пункта определяются по формуле:

Z

УДС

=





M

m 1

Z

mч

= Z

1ч

+ Z

2ч

+ … + Z

Mч

. (2.228)

Формула (2.227) в раскрытом виде имеет вид:

221

Z

m

=





H

h 1

(Z

h

/ C

h

) = Z

1

/ C

1

+ Z

2

/ C

2

+ … + Z

H

/ C

H

.

(2.229)

где С

h

- длительность цикла СР на h-перекрёстке, с; h=1,2,…,H- номер пере-

крёстка.

Если будет известен размер задержек за один час работы светофорных

объектов на одной магистрали, то можно подсчитать задержки за сутки и со-

ответственно за год. За сутки временной размер задержек ТС на одном h-

перекрестке составит:

Z

hc

= Z

h

∙ 13 =





4

1j

13 Z

jk

/ C

h

, (2.230)

Примечание: Принято что регулирование движения осуществляется в те-

чение 13 часов, а в остальные 11 ч СО работают в режиме жёлтого мигаю-

щего.

Например: Zhc = 10,5 ∙ 13 = 136,5 ч/сутки, где Zh = 10,5 ч/ч (см. расчёт

выше)

За один год временной размер задержек ТС лишь на одном перекрестке

составит:

Z

hг

= 365 ∙ Z

hc

, (2.231)

Z

hг

= 365 ∙ Z

hc

= 365 ∙ 136,5 = 49 822,5 ч/год.

Таким образом, в течение года временные задержки ТС у стоп-линии со

всех четырех направлений лишь одного перекрестка при вышеуказанной ин-

тенсивности движения составляют 49 822,5 часа. Таких задержек на перекре-

стке с двухрядным, трехрядным движением ТС будет соответственно в 2-3

раза больше, чем на перекрёстке с однорядным движением.

Задержки очереди ТС со всех направлений одного h-перекрестка с двух-

рядным движением на т-магистрали за один час работы в часах определяют-

ся по формуле (в раскрытом виде):

Z

hт

=





K

k 1





4

1j

Z

jkh

/С

h

= Z

11

/С

h

+ Z

12

/С

h

+ Z

21

/С

h

+ Z

22

/С

h

+ Z

31

/С

h

+ Z

32

/С

h

+

Z

41

/С

h

+ Z

42

, /С

h

ч/ч. (2.232)

где Z

jk

– временной размер задержек очереди на k-й полосе j-го направления,

222

с/ц, Z

jk

/С, ч/ч.

Формулу(2.226) или (2.22) определения задержек ТС на m-магистрали

можно представить в несколько ином раскрытом виде: Z

mУДС

, ч/ч

Z

mУДС

=





Н

h 1

Z

hm

= Z

1m

+ Z

2m

+ … + Z

hm

, (2.233)

Временные задержки очередей ТС на перекрестках магистралей дорож-

ной сети населенного пункта за сутки определяются по формуле

Z

УДС

= 13





M

m 1

Z

mУДС

= Z

1УДС

+ Z

2УДС

+ … + Z

МУДС

, (2.234)

где Z

mУДС

=





Н

h 1

Z

hm

= Z

1m

+ Z

2m

+ … + Z

hm

; m=1,2,…, М – номер магистрали;

13- количество часов работы СО магистралей населённого пункта.

За сутки (13 часов) работы СО задержки ТС на h-перекрестке в часах

при многорядном движении составят Zhmc, ч/сутки (см. уравнение (2.232)):

Z

hmc

=





K

k 1





4

1j

13 Z

jkh

/ C

h

= 13 Z

11h

/ C

h

+ 13 Z

12h

/ C

h

+ … + 13Z

1Kh

/ C

h

+

+ 13Z

21h

/ C

h

+ 13Z

22h

/ C

h

+ … + 13Z

2Kh

/ C

h

+ (2.235)

+ 13 Z

31h

/ C

h

+13 Z

32h

/ C

h

+ … +13 Z

3Kh

/ C

h

+

+ 13Z

41h

/ C

h

+ 13Z

42h

/ C

h

+ … + 13Z

4Kh

/ C

h

.

За год временные задержки очередей ТС на h-перекрестке при много-

рядном движении будут Z

hmг

, ч/год (см. уравнение 2.235):

Z

hmг

= Z

hс

∙ 365. (2.236)

За год временные задержки ТС на

m

-магистрали при многорядном дви-

жении определяются следующим образом Z

mУДСг

, (см. уравнение 2.235):

Z

mУДСг

=





H

h 1

365 Z

hcm

= 365Z

1cm

+365 Z

2cm

+ … +365 Z

Hcm

, (2.337)

На дорожной сети n-населённого пункта за сутки задержки составят:

- за сутки (см. уравнение 2.227 и 2.228):

ZУДСс =





M

m 1

ZmУДСг = Z1УДСс + Z2УДСс + … + ZMУДСс, (2.238)

- за год (см. уравнение (2.238))

ZУДСг = 365 ZУДСс, ч/год (2.239)

На дорожных сетях региона, состоящего из n- населённых пунктов и m- ма-

223

гистралей, задержки ТС в один час работы СО могут быть определены (см.

уравнение (2.227), (2.228)) так:

Z

rчч

=





M

m 1

ZmчR +





N

n 1

ZnУДС, (2.240)

Здесь первое слагаемое суммирует магистрали региона не входящие в

состав магистралей населённых пунктов. Выражение (2.240) можно предста-

вить в раскрытом виде:

ZRч = (Z1чR + Z2чR +…+ ZмчR) + (Z1удсч + Z2удсч +…+ Zn удсч) (2.241)

Задержки ТС на дорожных сетях региона составят:

- за сутки работы СО (см. уравнения (2.240) и (2.241)):

ZRс =





M

m 1

13Zmcr +





N

n 1

13ZnУДС, (2.242)

- за год

ZRr = 365ZRC = 365(





M

m 1

13Zmcr +





N

n 1

13ZnУДС), ч/год (2.243)

Выражение (2.243) можно представить в раскрытом виде:

Z

Rr

= 365(13Z

1чR

+ 13Z

2чR

+…+13Z

МчR

)+

+365(13Z

1УДСс

+13Z

2УДСс

+…+13Z

NУДСс

). (2.244)

Представленная здесь методика одного из главных функциональных

критериев оценки качества О и УДД, во первых, дает возможность специали-

стам воспользоваться разработанными методами в доступной форме для вне-

дрения, и во вторых, к сокращению сроков её адаптации в процессе внедре-

ния. Наличие полученных задержек ТС на любых пространствах позволит не

только выявить узкие места в О и УДД, но и разработать перечни соответст-

вующих мероприятий исключающих сверхнормативные задержки, снизить

стоимость одного километра пути и часа ездки, а так же найти механизмы

управления ими.

Приведенные здесь в методике механизмы оценки задержек могут быть

адаптированы в системах АСУД с незначительными усовершенствованиями

к конструктивном аспекте, на любых пространствах.

Таким образом данная методика, по нашему мнению, должна служить

оценочным инструментом качества О и УДД и повышения эффективности

224

управления дорожным движением.

2.6.6.Теоретические принципы возникновения заторовых состояний [67]

Резкий рост автомобильного парка в условиях отставания в развитии

дорожных сетей, как правило, приводит к несоответствию спроса на дорож-

ные услуги их предложению.

Если в состоянии затора расстояние между передними бамперами ТС

складывается из длины ТС l

a

и продольного зазора l

0

=1÷3м [141], то l

a

+l

0

в

процессе безопасного движения это пространственное расстояние на перего-

не несколько возрастает, и будет соответствовать размеру продольного ди-

намического габарита L

d

[141]:

0

2

)( ll

j

v

ttvL

a

уст

crd



,

где v - скорость движения, м/с; j

уст

– замедление, j

уст

=5 или 5,8 м/с

2

;

t

r

=0,1÷0,6 с – реакция водителя; t

с

– продолжительность приведения тормоз-

ной системы в рабочее состояние, с, t

r

+ t

с

≈0,8 с. [141]

При таком неравенстве l

a

+l

0

< L

d

, где

0

2

)( ll

j

v

ttvL

a

уст

crd



участок магистрали функционирует нормально, заторы отсутствуют. Здесь l

0

значительно превышает установки [141] l

0

=1÷3м. в противном случае, когда

l

a

+l

0

≥ L

d

, т.е. когда L

d

значительно меньше его правой части

0

2

)( ll

j

v

ttvL

a

уст

crd

 , то уровень БДД снижен и при значительной разни-

це заторовое состояние может иметь место.

Это также можно рассмотреть и на временной размерности:

jk

a

v

ll





1

0





. В этом случае перегон функционирует нормально. В против-

ном случае, когда

jk

jkajk

v

ll





1

0





(2.245)

на перегоне по сути дела это является предвестником возможного заторового

состояния.

225

Перекресток является участком дорожной сети, где сконцентрированы

маневры ТС, связанные с изменением их направлений движения и осуществ-

ляется поочередный пропуск ТПП.

На регулируемом перекрестке заторовое состояние возникает только

тогда, когда длительностей циклов С, а точнее их разрешающих тактов t

зел

недостаточно для пропуска транспортных потоков (ТП) λ

jk

по j–му направле-

нию, k–й полосе движения [85]:

rq

Tt

С

r







1

2

0

, с;

)(

0

TC

rq

q

t

зел







, с/ц;

jkзел

tt

0

 , (2.245)

когда размер очереди у стоп-линии и ее временная длина больше той, на ко-

торую рассчитан цикл С

р

:

q

TCTt

n

i

jkr

j











1

)]([

4

1

00

0



,

0

000

0

1

)](2[

q

qTCTt

t

r

jk









, (2.246)

когда λ

maxjk

< λ

jk

rзел

jk

C

tt





3600)(

max



 .

где Т

0

– суммарная длительность промежуточных тактов (желтых сигналов),

с, которая должна быть достаточна ТС для освобождения перекрестка с j –

направлений пересекающим стоп-линию в момент смены зеленого сигнала на

желтый; r и q – динамические характеристики ТП (гармоничные величины)

соответственно по четным и нечетным направлениям движения; t

зел

- дли-

тельность разрешающего такта, с/ц; t

0

- временная длина очереди при пере-

сечении стоп-линии на j – направлении, с/ц; n

0jk

– размер образовавшейся

очереди у стоп-лини на j – направлении, k – полосе движения, ТЕ/ц; β – доля

запрещающего такта, β=1-α;

rq

q







.

Если рассчитывать длительность цикла С на размер ТП в средних зна-

чениях С

j



=n

0jk

, а в некоторые периоды это равновесие, т.е. равенство, будет

нарушено в сторону увеличения, то исход тот же, т.е. интенсивность прибы-

тия к стоп-линии λ

jk

больше той

jk



, которая была принята при расчете дли-

тельности цикла С, разрешающего такта t

зел

и размера очереди n

0jk

, а поэтому

jkjk

jk

зел

nC

t

0







,

jkjk

Cn





0

, (2.247)

226

В условиях, когда левые части указанных выше неравенств будут рав-

ны правым, то заторовые состояния будут исключены, и светофорный объект

будет функционировать нормально. В случае, когда λ

jk

будет меньше, нежели

jk



, которая заложена в С, t

зел

, n

0jk

то возникнут неоправданные задержки.

Допустим, что средний временной интервал между передними бампе-

рами ТС будет τ

jk

=2,1 с/ТЕ, а

с

rq

Tt

С

rq

Tt

rr

4

1

2

1

2

00













,

то за каждый цикл остаются не пропущенными по одной транспортной еди-

нице (ТЕ) на каждой полосе всех направлений в случае одинаковой их транс-

портной загрузке. В течение 20 циклов образуется заторовое состояние из 20

не пропущенных ТС. По сути, каждая очередь транспортных средств при

этом задерживается у стоп-линии более одной длительности цикла светофор-

ного регулирования.

Поскольку пропускная способность одной полосы движения регули-

руемого перекрестка, обозначенная через максимальную интенсивность дви-

жения по этой полосе λ

max

соответствующая как дорожным условиям, режи-

мам движения, так и регламенту светофорного регулирования определяется

посредством уравнения [2.193], но в несколько уточненном виде:

jkh

rзел

jkh

C

tt





3600)(

max



 , (2.248)

то следует отметить, что реакция водителя t

r

при их высоких профессиональ-

ных качествах и культуре движения равна нулю.

При заторе в движении ТП интенсивность движения λ

jkh

будет несколь-

ко больше, чем λ

maxjkh

, отражающей пропускную способность полосы движе-

ния от ее номинальной величины на Δλ

jkh

. Значит, правая часть уравнения

(2.248), отражающая номинальную пропускную способность, будет на Δλ

jkh

меньше от λ

jkh

. Здесь главное значение имеет длительность цикла светофора

С, находящаяся в линейной зависимости от λ

jkh

и λ

maxjkh

, λ

jkh

> λ

maxjkh

.

Чтобы не было заторового состояния в программно-методическом ас-

пекте должно быть сохранено равновесие – равенство, но это чисто механи-

ческая, не логическая операция.

227

jkh

rзел

jkhjkh

СC

tt





)(

3600)(

max





 (2.249)

Чтобы избавиться от Δλ

jkh

следует осуществить перерасчет длительно-

сти цикла СР с учетом увеличения интенсивности движения на k полосе дви-

жения на Δλ

jkh

т.е. (

jkhjkh





max

).

В другом случае, представив уравнение (2.248) в следующем виде

3600)(

max rзелjkhjkh

ttС 



, когда часть ТС не успела пересечь стоп-линию за

длительность разрешающего такта t

зел

следует прибавить дополнительное

время t

зт

, назвав его заторовым временным интервалом в разрешающем так-

те, соответствующее λ

jkh

, т.е.

jkhjkhjkhзтrзел

Сttt



)(3600)(

max

 (2.250)

Соотношение (2.250) по сути, представляет временную длину суммар-

ной очереди, образовавшуюся у генерирующего перекрестка при пересече-

нии стоп-линии (правая часть равенства) и временной суммарный интервал

(длительность разрешающего такта) необходимый для пропуска образовав-

шейся очереди в течение часа СР (левая часть). Временной заторовый интер-

вал можно представить в виде формулы

)()(

rзелjkhjkhjkhзт

ttСt 



. (2.251)

Долю временного заторового состояния за час работы светофорного

объекта можно определить по формуле

с

С

tt

С

ttС

С

t

rзелjkhjkhjkh

rзелjkhjkhjkhзт

,

3600

)()(3600

3600

)()(

3600







(2.252)

С

ttt

rзел

jkhjkhjkh

зт

)(

3600







, (2.253)

Для определения количества не пропущенных ТС за время разрешаю-

щего такта следует разделить на временной интервал между передними бам-

перами τ

jkh

.

Можно определить количество не пропущенных ТС в течение разре-

шающего такта несколько иначе. Так, количество прибывших ТС за цикл СР

к стоп-линии светофорного объекта составляет С·λ

jkh

, ТЕ/с, а количество

228

пропущенных через перекресток в течение разрешающего такта будет

jkhrзел

tt



/)(  , ТЕ/цикл.

Таким образом, количество не пропущенных ТС через регулируемый

перекресток может быть определено следующим выражением, n

нпр





]/[

jkhrзелjkhнпр

ttCn









. (2.254)

Чем больше n

нпр

, тем выше интенсивность образования заторового со-

стояния. За количество циклов

С

3600

в течение часа работы светофорного

объекта, n

чпр

, ТЕ/ч:

 

C

ttCn

jkhrзелjkhчпр

3600

]}/[{





, (2.255)

или





]/3600[3600

jkhrзелjkhчпр

Cttn









. (2.256)

Можно эти величины определить через интегралы:









зел

tt

зтзтзтзт

dttftt

5

0

)( ,









max

5

)(



ф

прпрпрпр

dnnfnn . (2.257)

Формула (2.253) дает возможность количество не пропущенных ТС за

цикл, а формулы (2.254) и (2.255) - за

С

3600

циклов, а это и является интен-

сивностью образования затора в движении в течение часа работы СО. Зави-

симость заторового временного интервала t

зт

в разрешающем такте t

зел

и ко-

личества не пропущенных ТС n

пр

от интенсивности прибытия к стоп – линии

λ

jkh

представлена в табл. 2.2 и на рис. 2.29.

Таблица 2.2

Зависимость заторового временного интервала t

зт

в разрешающем такте t

зел

и коли-

чества не пропущенных ТС n

пр

от интенсивности движения λ

jkh

λ

jkh

,с/ТЕ 0,01

0,02

0,03

0,04

0,05 0,06 0,07 0,08 0,09

0,1 0,11

0,12

0,13 0,14 0,15 0,16

C 7,436

7,931

8,495

9,146

9,906

10,8 11,88

13,19

14,83

16,94

19,74

23,65

29,49

39,18

58,33

114,1

t

зел

, с 0,718

0,965

1,248

1,573

1,953

2,401

2,939

3,595

4,415

5,468

6,868

8,824

11,75

16,59

26,17

54,07

t

зт

, c

Δλ=1λ

0,109

0,233

0,374

0,537

0,726

0,951

1,219

1,548

1,958

2,484

3,184

4,162

5,624

8,045

12,83

26,78

Δλ=2λ

0,273

0,582

0,934

1,341

1,816

2,377

3,049

3,869

4,894

6,21 7,961

10,41

14,06

20,11

32,08

66,96

Δλ=3λ

0,436

0,931

1,495

2,146

2,906

3,802

4,878

6,191

7,831

9,935

12,74

16,65

22,49

32,18

51,33

107,1

229

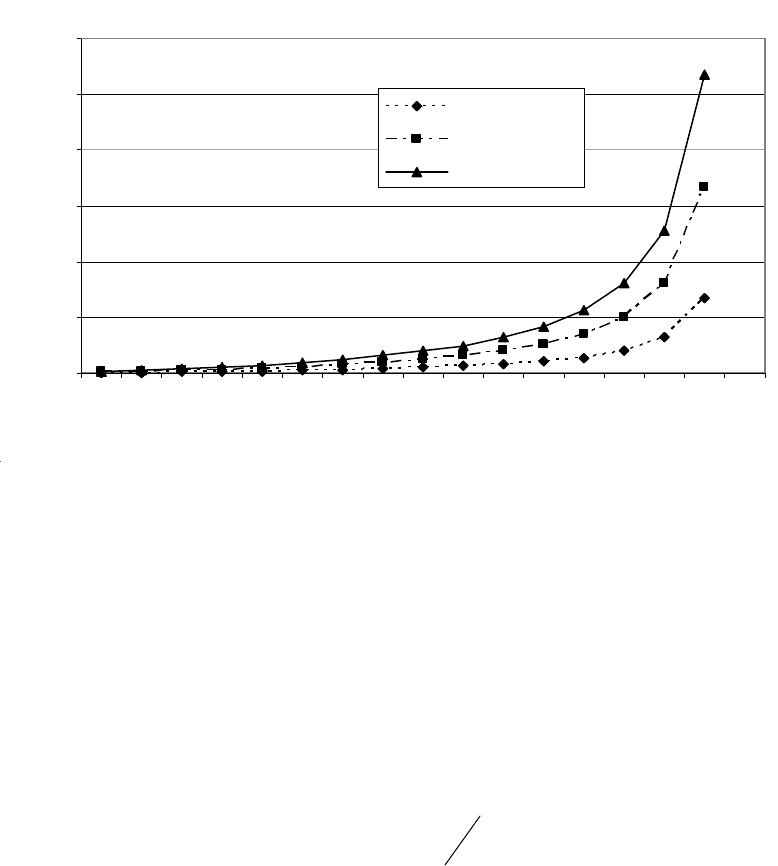
По данным табл. 2.2. или рис.2.29 достаточно просто определить коли-

чество не пропущенных ТС за цикл n

пр

= t

зт

/ τ

jk

.

Эти теоретические принципы выявления и соответственно упреждения

заторовых состояний без особых трудностей реализуются в автоматизиро-

ванных (адаптивных) системах управления дорожным движением, посредст-

вом настройки или установки дополнительных детекторов транспорта, несу-

щих информацию не только о превышении 1

0



зел

t

, но и обеспечении этого

равенства.

Как видим режим движения на СО, по сути, определяет потенциал по-

лосы движения: чем больше длительность цикла СР, тем выше пропускная

способность этой полосы и в целом перекрестка.

Вместе с этим, следует заметить, что недостаток проезжих частей также

является предвестником заторовых состояний. Эта проблема решается дове-

дением размеров полос движения проезжих частей до соответствия находя-

щегося на дорожной сети в пиковые периоды автотранспортных средств и их

плотности и интенсивности движения.

0

20

40

60

80

100

120

0,01 0,02 0,03 0,04 0,05 0,06 0,07 0,08 0,09 0,1 0,11 0,12 0,13 0,14 0,15 0,16

Интенсивность движения λ, c

Заторовый временной интервал, t

зт

, c

tзт,с (Δλ=1λ)

tзт,с (Δλ=2λ)

tзт,с (Δλ=3λ)

Рис. 2.29. Зависимость заторового временного интервала в разрешающем

такте t

зт

от интенсивности движения ТС λ

jkh

230

Живоглядов В.Г. Теория движения транспортных и пешеходных потоков

Подождите немного. Документ загружается.