Жариков В.А. Основы физической геохимии
Подождите немного. Документ загружается.

вариантов только один является стабильным и выбор его всецело определяется физико-
химической природой фазовых равновесий, их зависимостью от координатных
интенсивных параметров.
Отметим теперь некоторые особенности топологии диаграмм одновариантных
мультисистем с сингулярными равновесиями.
Подробное рассмотрение связи топологии диаграмм мультисистем с концентрационными
диаграммами, на основе которой возможен последовательный анализ сингулярных
равновесий, выходит за рамки настоящей работы. Поэтому ограничимся только указанием
тех осложнений, которые вносят сингулярные равновесия в строение диаграмм состояния
одновариантных мультисистем.
1. Поскольку каждое сингулярное равновесие содержит индифферентные фазы,
соответственно числу их увеличивается число нонвариантных точек, расположенных на
сингулярной
моновариантной линии.
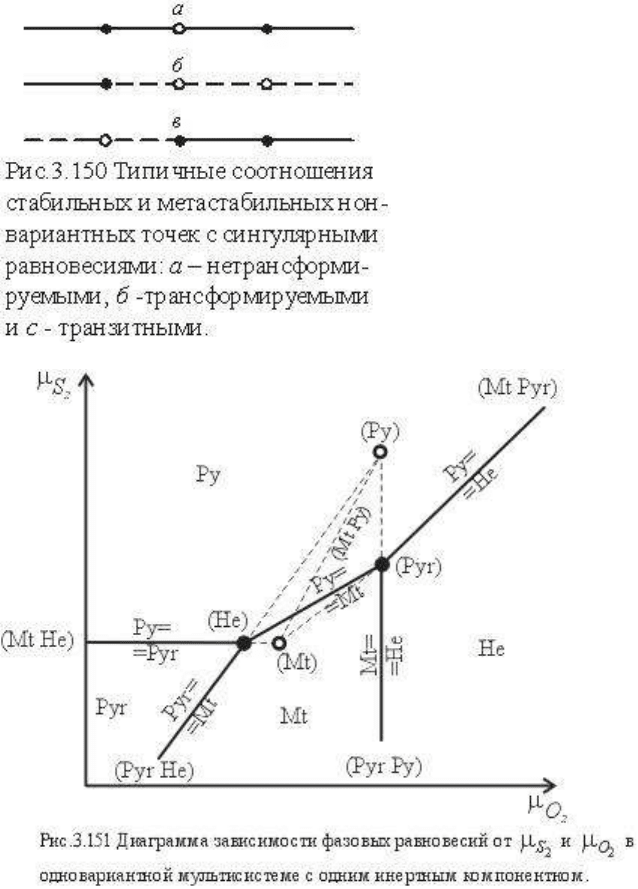
2. В одновариантной
мультисистеме
сингулярные равновесия
могут быть
нетрансформируемые,
трансформируемые и
транзитные, когда, будучи
для одной нонвариантной
точки
нетрансформируемым, для
другой точки это же
равновесие становится
трансформируемым.
Соответствующим образом
ведут себя и сингулярные
линии. На рис. 3.150
показаны соотношения
нонвариантных точек для
нетрансформируемого (а),
трансформируемого (б) и
транзитного (в)
сингулярных равновесий с
одной дополнительной
индифферентной фазой.
3. В системах с
сингулярными
равновесиями
метастабильные точки
могут содержать
стабильные сингулярные
лучи, которые, пересекаясь
с обычными
метастабильными лучами, могут образовывать метастабильные точки.
4. В том случае, если число сингулярных фаз в одновариантной мультисистеме равно r
1
=
k + 1, в системе появляются сингулярные нонвариантные точки (т.е. нонвариантные
равновесия с индифферентными фазами), координаты которых совпадают, а система
вырождается в систему c k-1.
В следующем разделе при рассмотрении примеров одновариантных мультисистем будут
затронуты и системы с сингулярными равновесиями.
Примеры диаграмм состояния одновариантных мультисистем
Рассмотрим несколько примеров диаграмм состояния мультисистем, обращаясь к уже
использованным парагенетическим ассоциациям.
1. Однокомпонентная система - Fe. Построим диаграмму состояния одновариантной
мультисистемы в координатах интенсивных параметров с фазами Pyr, Ру, Mt, и Не (см.
выше рис. 3.148). Топология диаграммы: число нонваринатных трехфазовых точек четыре
(h = C
r0
rs
= C
3
4
= 4), обозначенные (Не) (Mt) (Ру) (Pyr), число моновариантных
двухфазовых линий шесть (l = C
k+1
k+2-n
= C
r1
rs
= 6):соответственно l
1
(HeMt) Ру ↔ Pyr, l
2
(HePy) Pyr ↔ Mt, l
3
(He Pyr) Py ↔ Mt, l4 (Руr Ру) He ↔ Mt, l
5
(Pyr Mt) Ру ↔ Не и l
6
(Mt Ру)
Pyr ↔ He, четыре однофазовых поля (C
k
k+2-n
= C
r2
rs
= 4), отвечающих областям
стабильности Pyr, Py, Mt и Не. Для построения качественной диаграммы, как было
сформулировано выше, достаточно знать положение двух нонвариантных точек и
принадлежащих этим точкам моновариантных линий. В предыдущем разделе (см. рис.
3.127) мы построили диаграмму для ассоциации Рyr Py Mt, которая в рассматриваемой
системе представляет пучок нонвариантной точки (Не). Примем эту точку за одну из
необходимых для построения мультисистемы и нанесем соответствующий пучок (т.е.
нонвариантную точку и принадлежащие ей моновариантные лучи) на диаграмму μ
S2
- μ
O2
(см. рис. 3.151). В качестве другого необходимого пучка выберем пучок нонвариантной
точки (Руr), отвечающий распространенной природной минеральной ассоциации Ру Mt
Не. Соответствующая нонвариантная точка расположится на моновариантной линии l
3
(Не
Руr) Py ↔ Mt, проходящей через точку (Не). Нонвариантная точка (Руr) может быть
метастабильной или стабильной, располагаясь соответственно на метастабильном или
стабильном луче линии (Не Руr). Поскольку ассоциация Ру + Mt + Не обычна в природных
парагенезисах, принимаем точку (Руr) стабильной и располагаем ее (на произвольном
расстоянии) на стабильном луче (Не Руr). Нонвариантная точка (Руr) содержит линии l
3
(Не Руr) Py ↔ Mt, l
4
(Руr Ру) Mt ↔ H и l
5
(Руr Mt) Ру ↔ He
Линия (Не Руr) - общая для двух точек и уже нанесена на диаграмму, необходимо
рассчитать и нанести две оставшиеся моновариантные линии. Рассчитываем уравнение
реакции и определяем углы наклона линий:
(Pyr Py) 2Fe3О4 + 1/2 O
2
= ЗFе
2
O
3
,
, α = 90
o
(Рyr Mt) 2FeS
2
+ 1,5O
2
= Fe
2
O
3
+ 2S
2
,
, α = 38
o
В соответствии с правилами Скрейнемакерса стабильный луч l
5
(Pyr Mt) будет
расположен выше линии (Руr Не), а стабильный луч (Pyr Ру) - ниже линии (Pyr Не).

Наносим под соответствующими углами линии (Pyr Mt) и (Pyr Ру), подписываем
уравнения линий и проверяем правильность построения пучка (хотя бы по правилу углов).
Сопоставляя имеющиеся на диаграмме точки и линии с общей топологической схемой,
можно видеть, что для построения полной диаграммы состояния системы необходимо
определить положение еще двух нонвариантных точек (Ру), (Mt) и одной моновариантной
линии l
6
(Ру Mt) Руr=Не. Эти элементы находятся простым графическим построением.
Продолжая из имеющихся нонвариантных точек одноименные линии (т. е. не содержащие
одну и ту же фазу), на пересечении их получим нонвариантные точки, не содержащие эти
фазы. Так, на пересечении линии (Не Mt) из точки (Не) с линией (Pyr Mt) из точки (Pyr)
расположится точка (Mt); на пересечении линии (Не Ру) и линии (Pyr Ру) расположится
точка (Ру). Обсуждаемые пересечения произойдут между метастабильными лучами
линий, соответственно точки (Mt) и (Ру) будут метастабильными. Наконец, между
точками (Ру) и (Mt) будет проходить метастабильная линия l
6
(Ру Mt), нанесением
которой завершится построение диаграммы. Обозначив однофазовые дивариантные поля,
получим диаграмму состояния четырехфазовой одновариантной мультисистемы Fe - μ
S2
-
μ
O2
, которая показывает зависимость фазовых равновесий от величин химических
потенциалов серы и кислорода.
Анализируя диаграмму, легко убедиться в
соответствии ее сформулированным выше
топологическим правилам одновариантных
мультисистем. Диаграмма имеет две
метастабильные тoчки. Каждая моновариантная
линия проходит через две точки, причем на
диаграмме присутствуют все три возможных
варианта соотношений точек на линии.
Дивариантные поля, перекрывающие
метастабильные точки (Ру) и (Mt), представляют
поля стабильности этих фаз и т.д. Мы отмечали, что
одновариантная мультисистема имеет два варианта
диаграммы состояния. Второй, метастабильный,
вариант диаграммы представлен на рис. 3.152. Этот
вариант, напротив, обозначает стабильность точек
(Ру) и (Mt) и метастабильность (Не) и (Руr). Все
элементы диаграммы при этом как бы повернуты на
180
o
. Легко видеть, что этот метастабильный вариант противоречит элементарным
физико-химическим соотношениям: поле Ру, например, располагается в области высоких
μ
O2
, а поле Не - в области высоких μ
S2
т.д.
Наконец, мы отмечали, что в том случае, когда известны константы уравнений
моновариантных реакций (или, что то же, термодинамические характеристики фаз и их
зависимости от μ
S2
и μ
O2
), для построения полной диаграммы состояния мультисистемы
достаточно знать положение трех моновариантных линий, не входящих в один пучок. В
справедливости этого нетрудно убедиться, обратившись к диаграмме (рис. 3.151):
пересечение линий l
2
(Не Ру) l
3
(Не Pyr), l
4
(Руr Ру) даст две необходимые нонвариантные
точки (и даже три - третья метастабильная (Py)), а поскольку в уравнение
соответствующих линиям реакций входят все фазы системы, термодинамические
характеристики которых известны, вычисление μ
O2
-μ
S2
координат всех других линий и
точек представляет чисто техническую задачу.

2. Бинарная система А1
2
O
3
-SiO
2
. Кроме андалузита, силлиманита, муллита и корунда, Т-р
диаграмма для которых показана на рис. 3.146, включим в рассмотрение еще кварц, и для
пятифазовой ассоциации построим Т-р диаграмму одновариантной мультисистемы.
Ограничимся схематической диаграммой, принимая, как и ранее, для простоты ΔS
реакции независимым от температуры и строя диаграмму по известным координатам
нонвариантных точек и углам наклона моновариантных линий. В соответствии с
правилом фаз и правилом сочетаний пятифазовая ассоциация бинарной системы
представляет одновариантную мультисистему (n = k + 2 - r
S
= 2 + 2 - 5 = -1), диаграмма
которой состоит из пяти (C
r0
rs
= C
k+2
k+2-n
= 5) нонвариантных точек, десяти (C
r2
rs
= C
k+1
k+2-n
= 10) моновариантных линий и десяти (C
r2
rs
= C
k
k+2-n
= 10) дивариантных полей.
Нонвариантые точки: h
1
(Q) Andl Sil Mul Cor; h
2
(Cor) Q Andl Sil Mul; h
3
(Andl) Q Sil Mul
Cor; h
4
(Sil) Q Andl Mul Cor; h
5
(Mul) Q Andl Sil Cor; моновариантные линии: l
1
(Q Andl)
Sil Mul Cor; l
2
(Q Sil) Andl Mul Сor; l
3
(Q Mul) Andl Sil Cor; l
4
(Q Cor) Andl Sil Mul; l
5
(Cor
Andl) Q Sil Mul;l
6
(Cor Sil) Q Andl Mul; l
7
(Cor Mul) Q Andl Sil; l
8
(Andl Sil) Q Mul Cor; l
9
(Andl Mul) Q Sil Cor; l
10
(Sil Mul) Q Andl Cor; дивариантные равновесия (обозначим их
только по присутствующим фазам): t
1
Andl Cor, t
2
Andl Mul, t
3
Andl Sil, t
43
Sil Mul, t
5
Sil
Cor, t
6
Q Andl, t
7
Q Sil, t
8
Mul Cor, t
9
Q Mul, t
10
Q Cor.
Из диаграммы составов (рис. 3.153) системы можно
видеть, что в системе существует сингулярное
равновесие Andl=Sil (Q Mul) (Q Cor) (Cor Mul), т.e.
линии l
3
, l
4
и l
7
имеют одно и то же уравнение
реакции и один и тот же наклон на диаграмме. Можно также определить, что для
нонвариантной точки h
1
(Q) эта сингулярная реакция нетрансформируема (сингулярное
равновесие занимает краевое положение на диаграмме составов) и она отобразится
двунаправленной моновариантной линией l
3
- l
4
. Для нонвариантной точки h
2
(Cor)
сингулярное равновесие трансформируемо (занимает центральное положение на
диаграмме составов) в однонаправленный моновариантный луч l
4
. Наконец, дивариантное
равновесие t
10
Andl Sil вырождено в моновариантную линию l
3
l
4
.
Для построения диаграммы одновариантной мультисистемы необходимо и достаточно
знать положение двух нонвариантных точек и принадлежащих им моновариантных линий.
Одна из стабильных нонвариантных точек h
1
(Q) и ее моновариантные линии нами уже
построены (см. рис.3.146). Поэтому для построения полной диаграммы нужно задать еще
одну нонвариантную точку. В качестве таковой выбираем стабильную точку h
2
(Cor) Q
Andl Sil Mul, T-p координаты которой (определенные экспериментально) составляют T =
726
о
C, p=3000 бар. Определим положение моновариантных линий. Линия l
4
(Q Cor)=l
7
(Q
Mul), Andl=Sil сингулярная общая с точкой h
1
(Q) и ее наклон известен (dT / dp = - 0.040 =
tg α
4
). Необходимо рассчитать углы наклона еще двух линий:
l
5
(Cor Andl)
3AlSi
2
O
5
=
SiO
2
+
Al
6
Si
2
O
13
,
Sil
Q
Mul
l
6
(Cor Sil)
3Аl
2
SiO
5
=
SiO
2
+
Аl
6
Si
2
O
13
,
Andl
Q
Mul

где ΔS и ΔV -
энтропийный и
объемный эффекты
соответствующих
реакций, которые мы с
приближением
принимаем
постоянными; η -
множитель
размерности. Как и
ранее (см. рис. 3.146),
для большей
наглядности изменим
масштаб оси T,
увеличив его в 20 раз,
тогда α
5
=47
o
(tg α
5
=
0,053*20 =1,06) и α
6
=11
o
(tgα
6
=0,010*20=0,2). На T-p
диаграмму (рис.3.154)
нанесем положение
нонвариантных точек
h
1
и h
2
и
принадлежащих им
моновариантных линий l
1
, l
2
, l
3
, l
4
. В соответствии с объемным и тепловым эффектом
реакций подписываем моновариантные линии, и по правилам легко определяем
стабильные и метастабильные лучи. Причем лучи l
4
(Q Cor)= l
7
(Cor Mul) - сингулярный
однонаправленный, поэтому точка (Cor) имеет три моновариантные линии. Строим
оставшиеся элементы диаграммы. На пересечении метастабильных лучей l
2
(Q Sil) и l
6
(Cor Sil) расположится метастабильная точка h
4
(Sil). На пересечении метастабильных
лучей l
1
(Q Andl) и l
5
(Cor Andl) в бесконечности, поскольку лучи l
1
и l
5
параллельны,
находится метастабильная точка h
3
(Andl). Из точки h
4
в точку h
3
идет метастабильная
линия l
8
(Sil Andl). Пятая нонвариантная точка h
5
(Mul) располагается на пересечении
одноименных, безмуллитовых лучей, выходящих из других уже построенных
нонвариантных точек. Однако в связи с тем, чтo известные лучи l
3
(Q Mul) и l
7
(Cor Mul)
сингулярны и совпадают, не давая пересечения, на котором расположена h
5
для
нахождения последней нужен дополнительный луч. На диаграмме таким дополнительным
лучом выбран l
10
(Sil, Mul), пересечение которого с метастабильными l
3
и l
7
дает
метастабильную точку h
5
. Наконец, из метастабильной h
5
к метастабильной h
3
идет
метастабильный луч l
8
(Andl Mul). Завершая построение диаграммы, нанесем для каждого
поля бинарные диаграммы состав - парагенезис, которые характеризуют стабильность
восьми дивариантных равновесий: в поле I - t
1
Andl Cor t
6
Q Andl, в поле II - t
5
Sil Соr t
7
Q
Sil, в поле III - t
4
Mul Sil t
7
Q Sil t
8
Mul Соr, в поле IV - t
9
Q Mul t
8
Mul Cor и в поле V - t
3
Andl
Mul t
6
Q Andl и t
8
Mul Cor (первыми обозначены и выделены характеристические
парагенезисы каждого поля диаграммы).
Представленная диаграмма характеризует Т-р равновесия безводных алюмосиликатов,
кварца и корунда и их парагенезисов в высокотемпературной части системы Аl
2
O
3
- SiO
2
.
Диаграмма построена по экспериментальным значениям координат нонвариантных и
моновариантных линий (Жариков и др., 1973). Эти данные показывают Т-р пределы

устойчивости муллита, андалузита, силлиманита подтверждают известную по природным
наблюдениям метастабильность ассоциации Q+Cor. Заметим, что пocледний признак мог
быть использован для предварительного разделения равновесий на явно метастабильные,
содержащие кварц и корунд) и другие, возможные, подлежащие топологическому
анализу. Такой петрогенетический подход, несомненно, следует всегда использовать при
построении диаграмм, если только существует твердая уверенность или осознанная
необходимость проверки стабильности определенных нонвариантных ассоциаций.
Особенно целесообразен подход при анализе
многовариантных мультисистем.
3. В качестве еще одного примера используем
рассмотренную Д.С.Коржинским (1957) часть системы
CaO-MgО-SiO
2
-H
2
O-CO
2
. Минеральная ассоциация
состоит из шести фаз: тремолит (Ca
2
Mg
5
Si
8
О
22
(OH)
2
),
тальк (Mg
3
Si
4
О
10
(OH)
2
), cepпентин (Mg
6
Si
4
О
10
(ОН)
8
),
кварц (SiO
2
), кальцит (СаСО3) и доломит
(СаМg(СО3)
2
). Инертные компоненты: CaO, MgO и
SiO
2
. Вполне подвижные: H
2
O и CO
2
, химические
потенциалы которых представляют виртуальные
интенсивные параметры. Диаграмма составов
приведена на рис. 3.155. В соответствии с правилом
фаз рассматриваемая ассоциация является
одновариантной мультисистемой (n = k +2 - r
S
= 3 + 2 - 6 = -1). Топологические элементы
диаграммы следующие:
1) шесть нонвариантных пятифазовых точек (C
r0
rs
= C
k+2
k+2-n
= 6):
h
1
(Sp) Q Tr Та Dol Cal,
h
4
(Q) Tr Та Sp Dol Cal,
h
2
(Tr) Q Та Sp Dol Cal,
h
5
(Cal) Q Tr Та Sp Dol,
h
3
(Та) Q Tr Sp Dol Cal,
h
6
(Dol) Q Tr Та Sp Cal;
2) пятнадцать моновариантных четырехфазовых линий (C
r1
rs
= C
k+1
k+2-n
= C
4
6
= 15):
l
1
(Sp Q) Tr Та Dol
Cal,
l
2
(Sp Tr) Q Та Dol
Cal,
l
3
(Sp Та) Q Tr Dol Cal
l
4
(Sp Dol) Q Tr Та
Cal,
l
5
(Sp Cal) Q Tr Та
Dol,
l
6
(TrQ) Та Sp Dol Cal,
l
7
(Tr Та) Q Sp Dol
Cal,
l
8
(Tr Dol) Q Ta Sp
Cal;
l
9
(Tr Cal) Q Та Sp
Dol,
l
10
(Ta Q) Tr Sp Dol
Cal,
l
11
(Та Dol) Q Tr Sp
Cal,
l
12
(Ta Cal) Q Tr Sp
Dol,
l
13
(Q Dol) Tr Та Sp
Cal,
l
14
(Q Cal) Tr Та Sp
Dol
l
15
(Cal Dol) Q Tr Та
Sp;
3) двадцать дивариантных трехфазовых равновесий (C
r2
rs
= C
k
k+2-n
= C
3
6
= 20), которые мы
обозначаем по присутствующим фазам:

t
1
Q Tr Та,
t
2
Q Tr Dol,
t
3
Q Tr Cal,
t
4
Q Та Dol,
t
5
Q Та Cal,
t
6
Q Dol Cal,
t
7
Tr Та Dol,
t
8
Tr Та Cal,
t
9
Tr Dol Cal,
t
10
Та Dol Cal,
t
11
Q Та Sp,
t
12
Q Sp Dol,
t
13
Q Sp Cal,
t
14
Та Sp Dol,
t
15
Та Sp Cal,
t
16
Sp Dol Cal,
t
17
Q Tr Sp,
t
18
Tr Та Sp,
t
19
Tr Sp Dol,
t
20
Tr Sp Cal.
Из диаграммы составов можно видеть, что равновесия l
8
(TrDol), l
9
(TrCal), l
5
(DolCal),
Ta=Q+Sp представляют нетрансформируемое сингулярное равновесие, и соответственно
дивариантное равновесие t
11
Q Та Sp вырождено.
Составим матрицу одновариантной мультисистемы:
СaO
MgO
SiO
2
H
2
O
CO
2
Sp
0
6
4
4
0
Tr
2
5
8
1
0
Ta
0
3
4
1
0
Q
0
0
1
0
0
Cal
1
0
0
0
1
Dol
1
1
0
0
2
Вычеркивая поочередно по строке, получим матрицы всех шести пучков (нонвариантных
точек) диаграммы, а в свою очередь вычеркивая из них по строке, - определители,
отвечающие всем пятнадцати моновариантным линиям.
Однако для построения диаграммы состояния одновариантной мультисистемы
необходимо и достаточно знать положение только двух нонвариантных точек и
принадлежащих им моновариантных линий. Выберем для построения точки h
1
(Sp) Q Tr
Та Dol Cal и h
2
(Тr) Q Та Sp Dol Cal. Первая нонвариантная точка отвечает пучку
моновариантных линий, который уже рассчитан и построен выше (см. рис. 3.144).
Поэтому для построения диаграммы необходимо рассчитать и построить второй пучок,
отвечающий нонвариантной точке h
2
(Tr).
Матрица пучка:
СaO
MgO
SiO
2
H
2
O
CO
2

Sp
0
6
4
4
0
Ta
0
3
4
1
0
Q
0
0
1
0
0
Cal
1
0
0
0
1
Dol
1
1
0
0
1
Вычеркивая поочередно по одной строке, получим из левой, основной части матрицы
определители, отвечающие моновариантным линиям l
2
(Тr Sp), l
7
(Тr Та), l
6
(Tr Q), l
9
(Tr Cal),
l
8
(Tr Dol). Первая моновариантная линия l
2
(Tr Sp), общая для пучков h
1
и h
2
, рассчитана
выше. Рассчитаем уравнения реакций, отвечающих моновариантным линиям l
6
, l
7
, l
8
и l
9
.
Составив соответствующие определители, приравняв их к нулю и решив, уравнивая затем
содержание вполне подвижных компонентов (опускаем эти простые математические
выкладки), получим следующие уравнения моновариантных линий:
l
9
(Tr Cal) l
8
(Tr Dol):
2Mg
3
Si
4
O
10
(ОН)
2
+ 2H
2
O =
Mg
6
Si
4
O
10
(ОН)
8
+
4SiO
2
,
Ta
Sp
Q
, α
9
= 0
o
l
6
(Tr Q):
Mg
3
Si
4
O
10
(ОН)
2
+
3CaMg(CO
3
)
2
+ 3H
2
O =
Mg
6
Si
4
O
10
(ОН)
8
+
3СаСО3 + 3CO
2
,
Та
Dol
Sp
Cal
, α
6
= 45
o
l
7
(Tr Ta):
4SiO
2
+
6CaMg(CO
3
)
2
+ 4H
2
O =
Mg
6
Si
4
O
10
(ОН)
8
+
6СаСО3 + 6CO
2
,
Q
Dol
Sp
Cal
, α
6
= 56
o

Построим теперь диаграмму состояния мультисистемы в зависимости от величины
химических потенциалов, воды и углекислоты (рис. 3.156). Нанесем в координатах μ
CO2
-
μ
H2O
произвольно положение нонвариантной точки h
1
(Sp) и построим отвечающий ей
пучок моновариантных линий, обозначив уравнения реакций, стабильные и
метастабильные лучи (см. рис. 3.144).
Вторую нонвариантную точку h
2
(Тr) расположим на произвольном расстоянии от точки h
1
на стабильной части луча l2(Sp Tr) 17 и проведем принадлежащие точке h
2
(Тr)
моновариантные линии. Нетрансформируемое сингулярное равновесие l
9
=l
8
Ta+(H
2
O)=Sp+Q обозначится горизонтальной моновариантной линией, стабильной по обе
стороны нонвариантной точки. Подписав уравнение реакций, легко определим
относительно этой линии стабильные лучи l
6
(Tr Q) - ниже сингулярной линии и l
7
(Тr Та) -
выше ее. Обозначив уравнения реакций l
6
6 и l
7
убедимся в соблюдении всех
топологических правил и в точности построения опорных пучков.
Только графическими методами достраиваем диаграмму состояния одновариантной
мультисистемы. Установим сначала четыре нонвариантные точки. На пересечении
стабильных l
1
(Sp Q) и l
6
(Тr Q) находится стабильная точка h
4
(Q), на пересечении
стабильного сингулярного луча l
8
(Тr Dol) и стабильного луча l
4
(Sp Dol) - стабильная точка
h
6
(Dol). На пересечении метастабильных лучей l
3
(Sp Та) и l
7
(Тr Та) будет расположена
метастабильная точка h
3
(Та), и, наконец, пересечение метастабильного луча l
5
(Sp Cal) и
сингулярной линии l
9
-l
8
(в метастабильной части луча l
9
) образует метастабильную точку
h
5
(Cal).
Построим теперь недостающие моновариантные линии. Через каждую нонвариантную
точку трехкомпонентной системы проходят пять моновариантных линий. Четыре
нонвариантные точки построены пересечением двух моновариантных линий, однако легко
найти недостающие (три для каждой), помня, что каждая моновариантная линия проходит
через две нонвариантные точки, а все нонвариантные точки уже нанесены на диаграмму.
Нонвариантная точка h
4
(Q), кроме определивших ее положение линий l
1
(Q Sp) и l
6
(Q Тr),
содержит линии l
10
(Q Та), l
13
(Q Dol) и l
14
(Q Cal). Линия l
10
(Q Tr) проходит через
нонвариантные точки h
4
(Q) и h
3
(Та), поскольку точка h
3
метастабильная, то из точки h
4
на
нее пойдет метастабильный луч, а от нее стабильный луч l
10
. Линия l
13
(Q Dol) проходит
через точки h
4
(Q) и h
6
(Dol), последняя точка стабильна и на нее из h
4
идет стабильный
луч. Наконец, на метастабильную точку h
5
(Cal) из h
4
(Q) пойдет метастабильный луч l
14
, а
стабильный l
14
будет направлен в противоположную сторону.
Точка h
6
(Dol) содержит уже четыре моновариантные линии: два стабильных луча l
8
(Dol
Tr) и l
15
(Dol Cal), составляющих нетрансформируемую сингулярную линию, и две полные
моновариантные линии l
4
(Dol Sp) и l
13
(Dol Q). Пятая моновариантная линия l
11
(Dol Та)
пройдет соответственно через точки h
6
(Dol) и h
3
(Та), причем на последнюю будет
направлен метастабильный луч. Наконец, в метастабильной точке h
5
(Cal) осталось
построить последнюю моновариантную линию l
12
(Cal Тa), которая, соединяя две
метастабильныe точки h
5
(Cal) и h
3
(Та), будет тоже метастабильной.
Обозначим на моновариантных линиях уравнения этих реакций в соответствии с их
физико-химическим смыслом (парагенезис с большим содержанием вполне подвижного
компонента расположен со стороны большего химического потенциала).
Остается показать дивариантные равновесия, изобразив во всех полях диаграммы
треугольники состав - парагенезис, построение которых послужит одновременно
проверкой правильности всей диаграммы. Пронумеруем дивариантные поля диаграммы
(I-XII), тка же, как принято на рис. 3.143, и рассмотрим дивариантные равновесия каждого
поля, выделяя, как и ранее, штриховкой характеристические парагенезисы. Поле I
ограничено моновариантными линиями l
2
, l
4
и l
6
, реакции на которых однозначно
определяют парагенезисы Ta+Cal, Ta+Q+Cal и Ta+Dol. Характеристическим в данном
поле будет парагенезис t
10
TaDolCal, поскольку он однозначно определяет другие,
дополнительные, парагенезисы поля t
5
QTaCal и t
14
TaSpDol, которые мы достраиваем для
того, чтобы полностью покрыть область составов рассматриваемой системы (она
заключена, как легко видеть, в четырехугольнике Q-Sp-Dol-Cal). Заметим, что при
рассмотрении однопучковой диаграммы (см. рис. 3.143) в качестве характеристического
для поля I был принят парагенезис Q+Ta+Cal, получаемый в результате реакции l
4
. Для
мультисистемы этот парагенезис недостаточен для построения всех дивариантных
равновесий, так как остается неясным соотношение коннод Та Dol и Sp Cal. Обратим на
это внимание читателей: изменение фазового пространства или, проще, области составов
ни диаграмме может приводить к изменению характеристических парагенезисов.
