Жариков В.А. Основы физической геохимии
Подождите немного. Документ загружается.

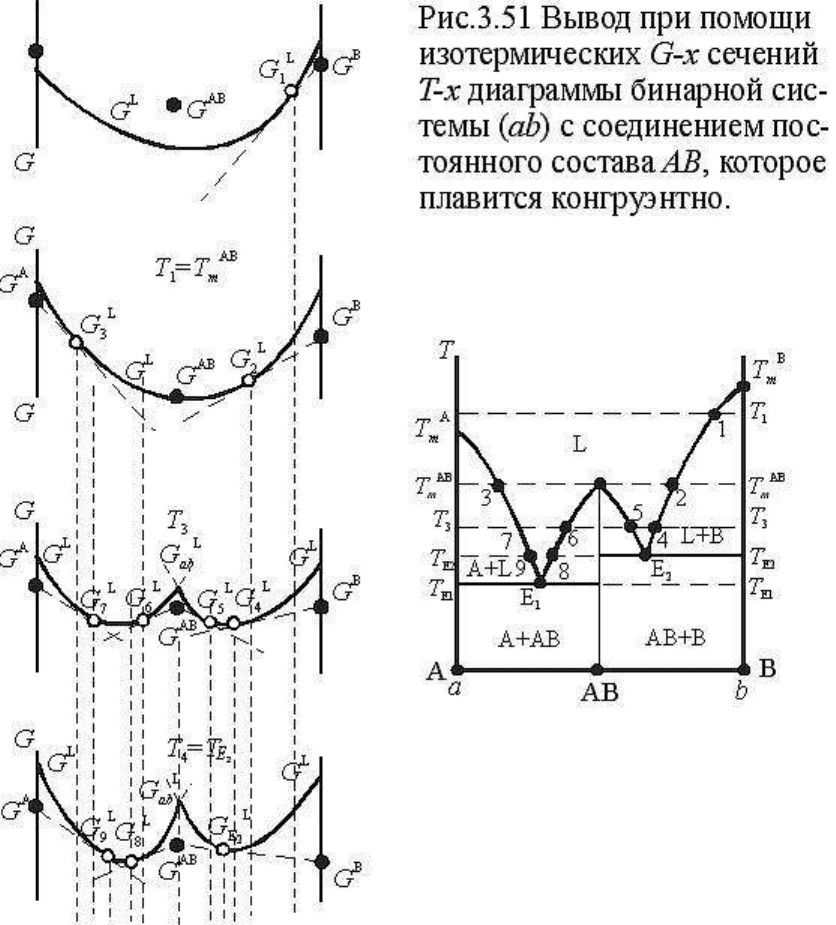
Особенность диаграмм этого типа состоит в том, что выбранные компоненты системы
образуют промежуточные по составу твердые фазы - соединения, которые также имеют
постоянный состав и плавятся конгруэнтно.
На Т-х диаграммах систем такого типа кривые плавления (в бинарных системах) и
поверхности плавления (в тройных системах) образуют особые или, как принято их
обозначать, сингулярные точки максимумов, число которых отвечает числу соединений.
Точка каждого такого максимума образуется путем пересечения кривых плавления ( и
сходящихся в этой точке поверхностей плавления), и состав их отвечает составу каждого
соединения. В зависимости от числа соединений в системе увеличивается число
эвтектических точек (можно показать, что число дополнительных эвтектических точек в
общем случае равно m(k-1) , где m - число соединений, а k - число компонентов, входящих
в состав соединений).
Вывод диаграмм плавкости для систем с конгруэнтно плавящимися соединениями при
помощи G-x диаграмм подобен выводу диаграмм с одной эвтектикой. Поэтому
ограничимся кратким обсуждением изотермических G-x сечений и T-x диаграммы в
части, отражающей особенности систем с соединениями.
На рис. 3.51 приведены необходимые изотермические сечения G-T-x диаграммы и T-x
диаграмма плавкости бинарной системы ab с соединением AB, которое плавится
конгруэнтно, т.е. расплав AB полностью отвечает ему по составу.

Ситуация при температуре T
1
отвечает рассмотренному выше при выводе бинарной
диаграммы с одной эвтектикой (см. рис. 3.36, сечение T
3
). Как видно из G-x и T-x
диаграмм, в области составов от а до точки 1 (G
L
1
) минимумом свободной энергии
обладает расплав, и для этого диапазона составов расплав представляет единственную
стабильную фазу. Для составов от точки 1 до b минимумом свободной энергии обладает
двухфазовое равновесие L + B (x
L
G
L
+ x
B
G
B
= G
min
), которое и является стабильным.
Дальнейшее понижение температуры, согласно уравнению (3.26) dG = - SdT + μ
a
dx
a
+
μ
b
dx
b
приводит к повышению G-потенциала фаз системы, причем большему для расплава,
чем для твердых фаз (напомним: S
L
a
> S
A
, S
L
b
> S
B
), и в результате возникнет ситуация,
изображенная на рис. 3.51 для T
2
. В области составов от b до точки 3 устойчива
двухфазовая ассоциация L + B. В области составов от a до точки 3, где x
A
G
A
+ x
L
G
L
3
=
min, стабильна ассоциация L + A. Между точками 2 и 3 устойчив расплав, но для точки ab,
где G
AB
= G
L
ab
, ΔG
AB-L
= 0, из этого (только из этого) состава при отводе тепла от системы
начнется кристаллизация соединения АВ. Согласно правилу фаз n
p
=k + 1-r=2 + 1-2=1
состояния L + A, L + B и L + AB - моновариантны; в системе происходит понижение
температуры и кристаллизация фаз A, B и AB в соответствующих диапазонах составов.
Появление в системе твердой фазы соединения AB приводит к разбиению системы на две
подсистемы L + A + AB и L + B + AB. На кривой GL появляется особая, сингулярная
точка G
L
ab
, образуемая пересечением двух кривых G
L
a
-G
L
ab
и G
L
b
-G
L
ab
, причем G
L
ab
> G
AB
.
Такая ситуация изображена для изотермы T
3
. Проведя на диаграмме G-x касательные из
точек G
B
и G
AB
к кривой G
L
b
-G
L
ab
получим составы расплавов, находящихся в равновесии
с твердыми фазами B и AB (соответственно, точки G
L
4
и G
L
5
на G-x диаграмме и,
проектируя, точки 4 и 5 на T-x диаграмме). Аналогично, проведя касательные из точек G
A
и G
AB
к кривой G
L
a
-G
L
ab
, получим составы расплавов сосуществующих с фазами A и AB
(точки G
L
7
и G
L
6
на G-x диаграмме, и точки 7 и 6 на T-x диаграмме). Пересечение кривых
ликвидуса плавления AB в подсистемах L + A + AB и L + B + AB (кривые 5-T
AB
m
и 6-
T
AB
m
) образует сингулярный максимум T
AB
m
, отвечающий температуре плавления чистой
фазы AB, имеющей, как отмечалось, постоянный состав.
Наконец, на изотерме T
4
в правой части системы получим единую касательную G
AB
-G
B
к
кривой G
L
b
-G
L
ab
, которая будет отвечать эвтектической точке в подсистеме AB-B
(значение G
L
E
на G-x диаграмме и E
2
в T-x системе). В подсистеме A-AB касательные из
G
A
и G
AB
к кривой G
L
a
-G
L
ab
определяют составы расплавов, сосуществующих с твердыми
фазами A и AB, - соответственно точки G
L
9
и G
L
8
на G-x диаграмме и точки 9 и 8 на T-x
диаграмме.
По аналогии легко представить, что при температуре T
E
единственная касательная,
проведенная из G
A
и G
AB
будет определять состав расплава в точке E
1
. В подсистеме ab-b
стабильны две твердые фазы AB и B. Получившаяся в итоге T-x диаграмма имеет две
эвтектические точки, и ее можно представить как две диаграммы с одной эвтектикой, если
выбрать ab в качестве независимого компонента.
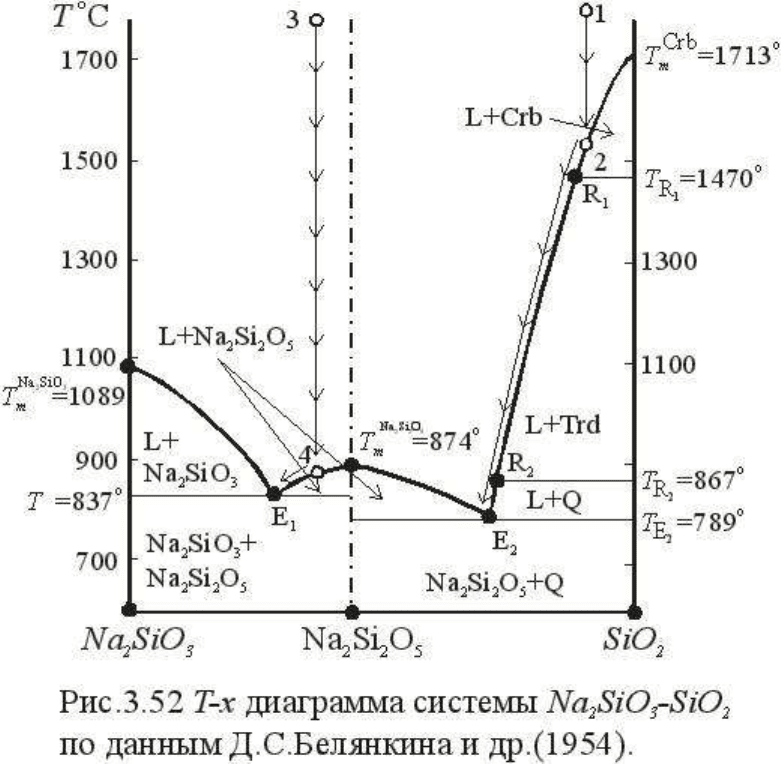
Рассмотрим в качестве примера диаграмму плавкости бинарной системы Na
2
SiO
3
-SiO
2
(рис.3.52). В этой системе существует соединение постоянного состава Na
2
Si
2
O
5
, которое
плавится конгруэнтно при T=874
о
C. Соответственно на кривой плавления Na
2
Si
2
O
5
имеется сингулярный максимум, и кристаллизация составов, менее богатых кремнеземом,
чем Na
2
Si
2
O
5
, будет заканчиваться в эвтектической точке E
1
, а более богатых
кремнеземом, чем Na
2
Si
2
O
5
, - в точке E
2
. В остальном схема кристаллизации аналогична
простым диаграммам с эвтектикой. Как отмечалось, рассматриваемую диаграмму можно
представить как две диаграммы, каждая с одной эвтектикой, если в качестве компонентов
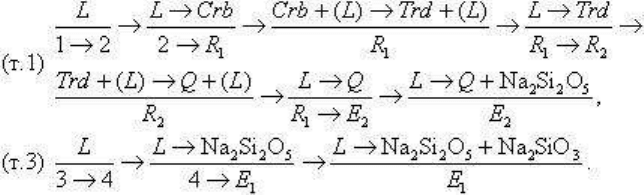
мы выберем Na
2
SiO
3
-Na
2
Si
2
O
5
и SiO
2
(см. пунктир на рис. 3.52). Еще одна особенность
диаграммы связана с существованием полиморфных разновидностей у кремнезема. При
понижении температуры будут происходить полиморфные переходы кристобалит -
тридимит (T
R
= 1470
o
C) и тридимит - кварц (T
R
= 867
o
C). Поскольку все эти фазы
постоянного состава, температура перехода (при постоянном давлении) строго
определена, и поля кристаллизации этих минералов на диаграмме отделены изотермами.
Полиморфные превращения протекают при нонвариантном состоянии системы (n
p
=k + 1-
r=2 + 1-3=0), поэтому состав расплава при температуре перехода (T
R1
и T
R2
) остается
постоянным.
Приведем схемы кристаллизации расплавов, состав которых отвечает фигуративным
точкам 1 и 3.
Фазовые соотношения, показанные на схемах и рис. 3.52, вполне очевидны и не требуют
дополнительных пояснений.
Трехкомпонентные системы с соединениями, плавящимися конгруэнтно, могут быть
разных видов: с двух-, с трехкомпонентными соединениями и более сложные, с
соединениями обоих видов.
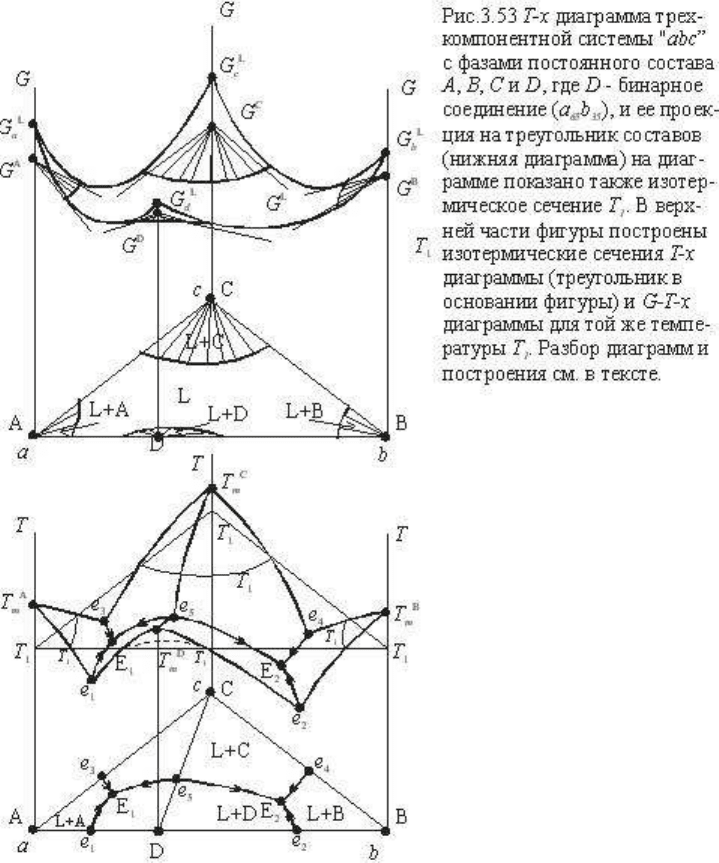
Вывод и построение диаграмм состояния этих систем при помощи G-T-x диаграмм
аналогичен приведенному выше выводу для бинарных систем, однако графические
построения на плоскости трехмерных изотермических G-x сечений G-T-x диаграмм
достаточно громоздки. Поэтому ограничимся одним более простым примером.
Рассмотрим трехкомпонентную систему abc с фазами постоянного состава A,B,C и D, где
D - двухкомпонентное соединение (a
65
b
35
). Для упрощения продемонстрируем обратную
задачу: по T-x диаграмме построим два изотермических (T
1
и T
2
) сечения G-T-x и T-x
диаграмм. На рис. 3.53 в нижней части показана T-x диаграмма системы и ее проекция на
треугольник составов (для большей наглядности масштаб в направлении вершины C
изменен, и в основании диаграммы лежит не равносторонний, а равнобедренный
треугольник). Точки T
A
m
, T
B
m
, T
C
m
и T
D
m
- это сингулярные максимумы Т-х диаграммы и
отвечают температурам плавления фаз постоянного состава A, B, C и D. Из этих точек
исходят кривые ликвидуса в бинарных системах, которые ограничивают поверхности
ликвидуса соответствующих фаз в трехкомпонентной системе. Обратим внимание на то,
что плоскость T
D
m
-D-C-T
C
m
представляет диаграмму бинарной системы D
(ab)
-C. Эта
плоскость разделяет систему abc на две подсистемы - ACD
(ab)
и BCD
(ab)
, каждая из
которых представлена обычно диаграммой плавкости с одной эвтектической точкой
(соответственно E
1
и E
2
). Точки e
1
- e
5
- эвтектические точки в соответствующих бинарных
системах; e
1
E
1
, e
3
E
1
, e
5
E
1
, e
2
E
2
, e
4
E
2
, e
5
E
2
- котектические линии. Котектические линии e
5
E
1
и e
5
E
2
, пересекаясь в точке e
5
, образуют сингулярный максимум.
Построим изотермическое сечение T
1
и, затем, соответствующую ему G-x диаграмму.
Проведя на T-x диаграмме плоскость T
1
, получим при пересечении ее с поверхностями
ликвидуса кривые, показывающие состав расплава, находящегося в равновесии с
соответствующими твердыми фазами при Т
1
: L + A, L + B, L + C и L + D (последняя
кривая, лежащая внутри T-x диаграммы, обозначена на ней пунктиром). Спроектировав
кривые ликвидуса на треугольник составов, получим изотермическое (T
1
) сечение T-x
диаграммы. Оно представлено в верхней части диаграммы как основание G-x диаграммы.
В соответствии с правилом фаз для изотермического сечения: n
T,p
=k-r. На диаграмме
присутствуют четыре моновариантных двухфазовых равновесия (L + A, L + B, L + C, L +
D, где состав расплава может изменяться вдоль изотермы ликвидуса) и одно дивариантное
поле (L), в пределах которого устойчива одна фаза - расплав.
Теперь для этого же изотермического сечения построим G-x диаграмму, для чего по
вертикали отложим G-потенциалы всех фаз системы. G - потенциал расплава представлен
вогнутой поверхностью, на которой спроектированы изотермы ликвидуса в равновесии с
четырьмя твердыми фазами L + A, L + B, L + C и L + D. Проведя от этих линий пучки
касательных, сходящихся на вертикальных аппликатах A, B, C и D, получим значения G-
потенциалов твердых фаз системы: G
A
, G
B
, G
C
и G
D
, которые меньше, чем значения G-
потенциалов расплава соответствующего состава. Легко представить, что при выводе T-x
диаграммы из G-T-x диаграммы (как было сделано выше), рассуждения были бы
обратными. Исследуя зависимость G=ƒ(T, x
a
, x
b
, x
c
) было бы показано, что при некоторой
температуре выше чем T
1
, во всем диапазоне составов G
L
= min и стабильной фазой
является расплав. Затем, при понижении температуры, поочередно для чистых составов A,
B, C и D G-потенциал расплава становился бы равным G-потенциалам твердых фаз и
начиналась бы их кристаллизация. Наконец, при Т
1
осуществилась бы ситуация,
показанная на рис. 3.53.
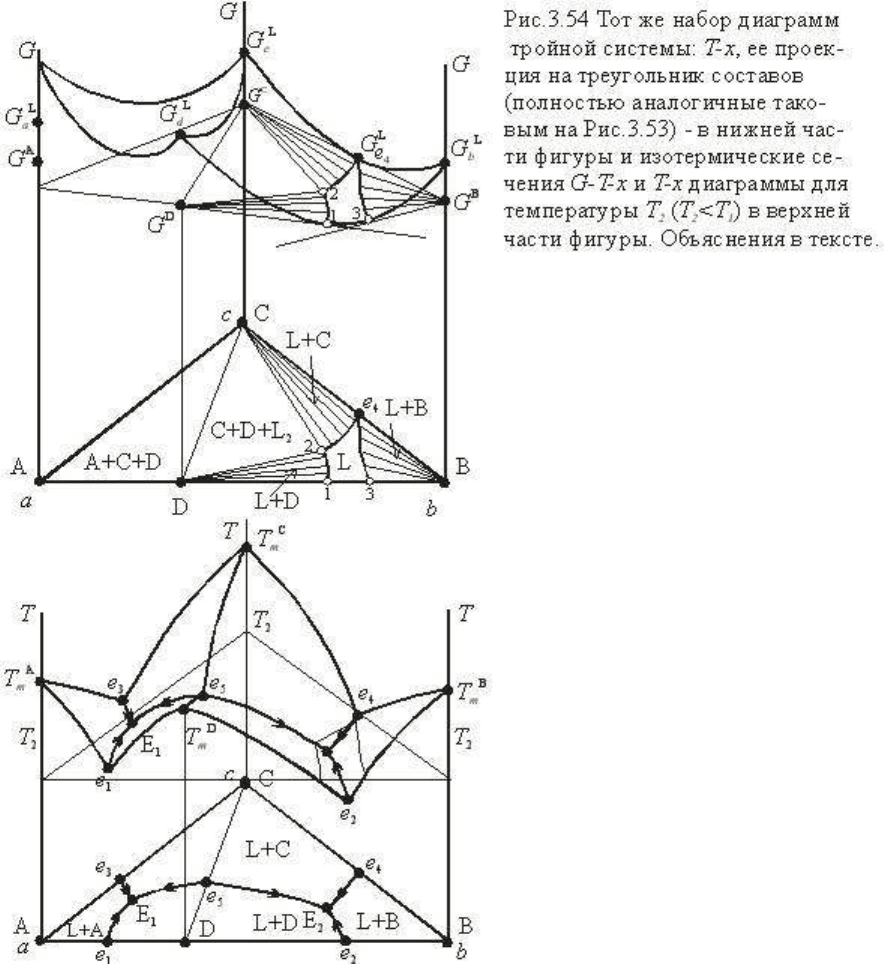
Рассмотрим еще одно изотермическое сечение T
2
той же диаграммы. На рис. 3.54, в
нижней части фигуры воспроизведена та же, что и на рис. 3.53, T-x диаграмма и ее
проекция на треугольник составов. На T-x диаграмме нанесено изотермическое сечение
T
2
, которое расположено ниже по температуре чем T
1
(рис. 3.53). Сечение в правой части
диаграммы пересекает поверхности ликвидуса фаз B, C и D, образуя соответствующие
линии ликвидуса (они обозначены изотермой T
2
). В левой части диаграммы сечение T
2
проходит в области субсолидуса. Изотермическое сечение T-x диаграммы (для
температуры T
2
) показано на треугольнике составов, являющихся основанием G-x
диаграммы (в верхней части рис. 3.54). Кривые ликвидуса, (1-2, 2-e
4
, e
4
-3),
спроектированные с T-x диаграммы, ограничивают дивариантное однофазовое поле
расплава. Соединив кривые ликвидуса с точками состава твердых фаз (кривая 1-2 с точкой
D, 2-e
4
с C и e
4
-3 с B) получим три моновариантных двухфазовых равновесия: L + D, L + C
и L + B - они выделены коннодами. Наконец, в центре и в левой части диаграммы
стабильны два нонвариантных трехфазовых равновесия C + D + L
2
и A + C + D.
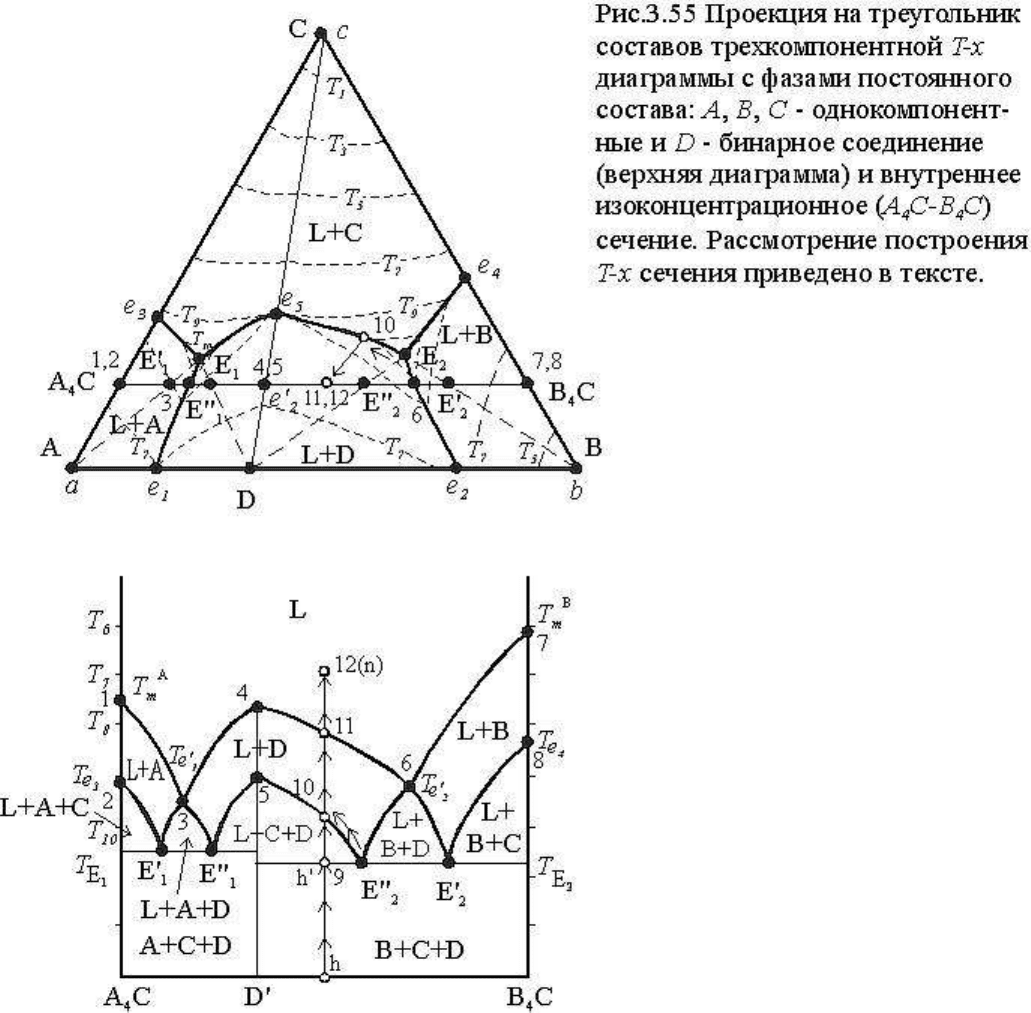
Завершая рассмотрение тройной T-x диаграммы с бинарным соединением, построим, в
качестве примера, одно изоконцентрационное сечение. На рис. 3.55, в его верхней части
представлена проекция на треугольник составов T-x диаграммы той же системы. На
проекции обозначены эвтектические точки, котектические линии, поля кристаллизации
фаз и нанесены некоторые изотермы: T
1
, T
3
, T
5
, T
7
, T
9
и T
10
. Выберем
изоконцентрационное сечение A
4
C-B
4
C и нанесем его на диаграмму.
Как было показано выше, изоконцентрационное T-x сечение отражает изменение фазовых
соотношений при кристаллизации (или плавлении) в тройной системе для любой
фигуративной точки сечения. Поэтому построение внутреннего T-x сечения производится
нанесением на диаграмму пересекаемых сечением топологических элементов трехмерной
T-x диаграммы и путем проекции на выбранное сечение других топологических
элементов (эвтектических точек, котектических линий), характеризующих изменение
фазовых соотношений в системе. Для осуществления последней цели проведем на
треугольной диаграмме плавкости линии AE
1
, DE и DE
2
, BE
2
, которые дадут на
пересечении с линией A
4
C-B
4
C точки E'
1
, E''
1
и E''
2
, E'
2
- суть проекции эвтектических
точек E
1
и E
2
. Две другие необходимые нам точки - проекции бинарных эвтектик e
3
и e
4
-
проектируются сторонами треугольника AC и BC.
Построим теперь в нижней части фигуры искомое сечение. Отложим по оси абсцисс
составы от A
4
C до B
4
C (что сделано в том же масштабе, что и на верхней диаграмме), по
ординате - температуру. На ординате T-A
4
C отложим две точки: 1 - точка пересечения
ликвидуса L + A выбранным сечением и 2 - проекция точки e
3
, которая на ординате
расположится при . Далее, двигаясь по сечению к составу B
4
C, получим координаты
проекции тройной эвтектики E
1
- точку E'
1
, располагающуюся при температуре .
Следующим (по мере движения к B
4
C) будет пересечение котектической линии e
1
E
1
,
которое даст нам точку 3, расположенную при температуре T
e1'
, которая немного меньше
T
9
(конечно, T
e1'
< T
e1
, на диаграмме T
e1'
= T
7
, а T
e1'
< T
9
). Следуя далее по сечению, на его
пересечении с линией DE
1
получим состав проекции E
1
'', который отложим на T-x сечении
при T
E1
. Следующим будет пересечение плоскости внутреннего T-x сечения с плоскостью
бинарной системы T-CD, которое выявит нам координаты точек 4 и 5. Точка 4 образуется
пересечением кривой ликвидуса L + D и показывает температуру плавления фазы D на T-x
сечении - T
D
m
. Точка 5 - проекция эвтектической точки e
5
- показывает температуру ее T
e5
(равную T
9
). Проведем ординату T-D' и отложим эти точки. Координаты всех
необходимых точек для построения T-x сечения в подсистеме ACD определены. Соединив
точки 1-3-4, получим сечение поверхностей ликвидуса L + A и L + D. Проведя кривые 2-
E'
1
и 3-E'
1
, отразим проекции котектических линий e
3
E
1
и e
1
E
1
(для последней от точки 3
до E
1
). Аналогичным образом, соединив точку 3 с E''
1
, и точку 5 с E''
1
, получим проекции
котектических линий e
1
E
1
(от точки 3) и e
5
E
1
. Наконец, проведя горизонтальную конноду
через точки E'
1
и E''
1
показывающую T
E1
, отделим субликвидус от субсолидуса: ниже по
температуре T
E
устойчивы только твердые фазы A + C + D. Обозначим остальные поля
диаграммы. Между линией T
E1
и проекциями котектик располагаются трехфазовые поля L
+ A + C, L + A + D и L + C + D (слева направо); между проекциями котектик и сечениями
ликвидуса (1-3 и 3-4) - двухфазовые поля L + A и L + D и выше по температуре -
однофазовое поле расплава.
Достроим T-x сечение от ординаты T-D
1
' до T-B
4
C. Поскольку строение T-x сечения
подсистемы B + C + D полностью аналогично рассмотренному, сделаем это кратко.
Перемещаясь по внутреннему T-x сечению от ординаты T-D' к ординате T-B
4
C,
последовательно зафиксируем точку E''
2
, являющуюся проекцией на сечении
эвтектической точки E
2
на точку D, точку 6, отмечающую пересечение котектической
линии e
2
E
2
, точку E'
2
- проекцию эвтектики E
2
на вершину B. Наконец на координате T-
B
4
C обозначатся две точки: точка 7 - пересечение линии ликвидуса L + B и точка 8 -
проекция бинарной эвтектики L + B + C (точка e
4
) на сечение A
4
C-B
4
C. Нанесем все эти
точки на T-x сечение, отложив на ординате соответствующие температуры T
E2
(для точек
E''
2
и E'
2
), T
e2'
, T
D
m
и T
e4
(для точек 6, 7 и 8). Соединив на T-x сечении точки 4-6-7,
обозначим линии ликвидуса L + D и L + B. Проведя линии между точками 5-E''
2
, 6-E''
2
, 6-
E'
2
и 8-E'
2
, отразим на диаграмме проекции котектических линий e
5
-E
2
, e'
2
-E''
2
(от точки 6 к
E
2
), e'
2
-E'
2
(тоже от точки 6 к E
2
) и e
4
-E'
2
. Наконец, проведя конноду через проекции точки
E''
2
и E'
2
, получим изотерму T
E2
, отделяющую субликвидус от субсолидуса в подсистеме B
+ C + D. Обозначим трехфазовые равновесия B + C + D (ниже конноды T
E2
), L + D + C, L
+ B + D и L + B + C (их поля ограничены коннодой T
E2
и проекциями котектических
линий), двухфазовые равновесия L + D (между кривыми 4-6 и 5-E''
2
, 6-E''
2
) и L + B (между
кривыми 6-7 и 6-E'
2
, 8-E'
2
). Наконец, выше кривых ликвидуса (4-6 и 6-7) расположено
однофазовое поле расплава.
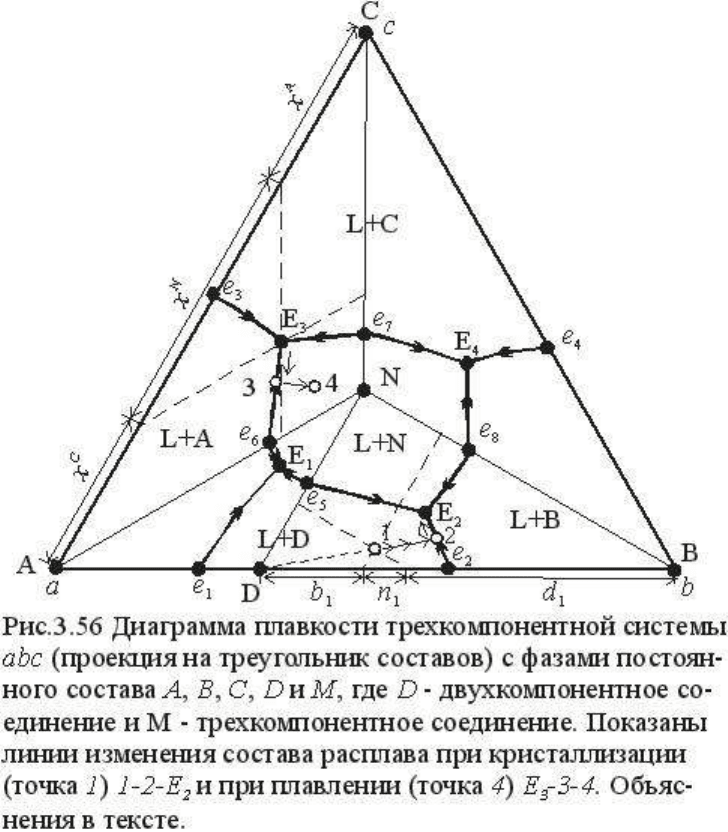
Анализ изменения фазовых соотношений при кристаллизации или плавлении мы
рассмотрим немного позже. Здесь же заметим, что для исчерпывающей характеристики T-
x диаграммы тройной системы с бинарным соединением нужны еще два внутренних
сечения - одно, пересекающее четыре котектические линии, и другое, расположенное в
поле L + C. Решение главной задачи - построение диаграммы плавкости тройной системы
с бинарным соединением - осуществится так же, как было показано выше на примере
тройной системы с одной эвтектикой. Рассмотрим кратко изменение фазовых
