Zelditch M.L. (и др.) Geometric Morphometrics for Biologists: a primer

Подождите немного. Документ загружается.

chap-08 4/6/2004 17: 25 page 208

chap-09 4/6/2004 17: 25 page 209

Multivariate analysis of variance

In Chapter 7 we discussed ordination methods, including one used to discriminate among

groups defined a priori, canonical variates analysis. In Chapter 8 we discussed sev-

eral computer-based statistical methods that use resampling techniques to test explicitly

whether an observed difference among groups is statistically significant. In this chapter

we present a second set of methods that take a somewhat different approach to testing

whether the observed difference is statistically significant. The approach used here is to

compare the observed value of a test statistic (e.g. the values of t for a difference between

two sample means) with the probability distribution of expected values for that statis-

tic under a particular theoretical model for the distribution of variation in a population.

This analytic approach is quite flexible, so the range of questions that can be addressed

by using it is broad. For example, an investigator might want to know whether males

and females differ in height. This is the simplest possible kind of question about differ-

ences between groups, because there is just one continuous variable (height), which is

a simple one-dimensional trait (i.e. it is a scalar), and there is just one categorical vari-

able (sex) with only two classes (male and female). Often the question is more complex,

as when the investigator is comparing shape differences among several species. This is

more complex because the continuous variable (shape) is multivariate (i.e. it is a vector)

and the categorical variable (species) has more than two classes (one for each species in

the study). The question can be made even more complex by considering multiple cate-

gorical variables (e.g. sexual dimorphism in several populations). Below we present the

analytic tests for answering both simple questions and more complex ones. Much of this

presentation follows expositions presented by Snedecor and Cochran (1967), Chatfield

and Collins (1980), and Morrison (1990); readers requiring further details are referred to

those works.

We begin this chapter with a brief review of groups and grouping variables. We then

present the simplest case, the test for a difference in one trait between two groups, and

the methods that would be used in such cases. We follow this with a series of more

complex analyses, and the more generalized methods that would be applied to them.

In the final section, we present instructions for performing the analyses discussed in this

chapter.

ISBN 0–12–77846–08 All rights of reproduction in any form reserved

chap-09 4/6/2004 17: 25 page 210

210 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

Groups revisited

A group is a set of individuals (a class) defined as sharing a state of a discontinuous trait.

In mammals and birds, “sex” is an example of a discontinuous trait that has two classes –

“male” and “female.” An individual is either one or the other as a consequence of having

one set of chromosomes or the other. Such traits may be called grouping variables, quali-

tative traits or categorical variables. All these names refer to the fact that the states of the

trait do not have intrinsic numerical values or an inherent order, but they can nonetheless

be used to sort individuals into groups or categories.

Frequently, traits that could be quantified are treated as categorical variables. “Diet”

and “locality” are examples of these kinds of traits. There are several reasons for treating

these traits as categorical variables: first, the available information may not be suffi-

ciently detailed to support a more finely graded analysis; second, the investigator may

not want to impose a hypothesis of ordering on the data; or third, the investigator may not

want to assume that all steps are of equal value. Under these circumstances, a quantifiable

trait may be treated legitimately as a categorical variable. The only requirement is that the

states of a particular variable are mutually exclusive – that is, each individual can belong

to only one group.

Analytic techniques

One simple trait, two groups

We begin with a simple case – a test for a difference in jaw size between male and female

adult squirrels collected at a single locality in western Michigan. Centroid size was com-

puted using the landmarks shown in Figure 9.1, and the observed values of jaw size and

their natural logs are given in Table 9.1. In this example, there is one continuous variable

(centroid size of the jaw) and one categorical variable (sex) with two categories or classes

(male and female). The question to be answered is whether jaw size differs between males

and females.

Figure 9.1 Outline of squirrel jaw, with landmarks.

chap-09 4/6/2004 17: 25 page 211

MULTIVARIATE ANALYSIS OF VARIANCE 211

The answer to this question can be obtained from a t-test. In this test, a variable known

as Student’s t (usually just ‘t’) is computed as a function of the difference between the means

of the two classes and variances around those means. The statistical model is the case in

which two samples of equal size are drawn from the same normal distribution. Under this

model, the difference between the sample means is expected to be zero and variance of the

difference is a function of the population variance and size of the samples. Thus:

t =

(<X

> −<X



2σ

(9.1)

Table 9.1 Jaw size variation in 58 squirrels from Allegan County, Michigan

Sex Centroid size ln centroid size Sex Centroid size ln centroid size

Female 53.0 3.97 Male 52.7 3.96

Female 51.8 3.95 Male 51.6 3.94

Female 51.5 3.94 Male 52.2 3.95

Female 48.6 3.88 Male 52.4 3.96

Female 50.7 3.93 Male 51.5 3.94

Female 51.4 3.94 Male 51.8 3.95

Female 52.0 3.95 Male 53.9 3.99

Female 50.3 3.92 Male 53.0 3.97

Female 51.7 3.95 Male 51.5 3.94

Female 52.2 3.96 Male 51.2 3.94

Female 50.6 3.92 Male 51.9 3.95

Female 51.8 3.95 Male 52.8 3.97

Female 51.3 3.94 Male 53.4 3.98

Female 52.7 3.96 Male 53.9 3.99

Female 50.6 3.92 Male 53.1 3.97

Female 52.6 3.96 Male 52.6 3.96

Female 51.1 3.93 Male 51.6 3.94

Female 50.4 3.92 Male 51.5 3.94

Female 51.0 3.93 Male 52.2 3.96

Female 51.4 3.94 Male 51.4 3.94

Female 52.0 3.95 Male 51.8 3.95

Female 52.0 3.95 Male 52.6 3.96

Female 50.4 3.92 Male 52.4 3.96

Female 51.9 3.95 Male 51.7 3.95

Female 53.0 3.97

Female 52.9 3.97

Female 51.0 3.93

Female 52.4 3.96

Female 51.8 3.95

Female 53.0 3.97

Female 51.7 3.95

Female 52.8 3.97

Female 51.5 3.94

chap-09 4/6/2004 17: 25 page 212

212 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

where <X

> is the expected value (mean) of group 1, <X

> is the expected value of

group 2, σ

is the variance, and N is the sample size. Under the conditions of the model

(a single population with a normal distribution), t has a known probability distribution,

which approaches the normal distribution as N increases. Thus, the t-test evaluates the

probability that two samples with means differing by the observed amount could be drawn

by random sampling from a single population with the given variance.

In most studies (as in the squirrel jaw example) the two classes are represented by samples

that have different variances and different numbers of individuals. This creates the problem

of deciding what values to use to compute the standard error. The usual solution to this

problem is to treat the two sample variances as estimates of one population variance, which

is consistent with the model underlying the t-test. Accordingly, the sample variances (s

)

are weighted by their respective sample sizes (N

) to compute a “pooled” estimate of the

standard error, as shown in Equation 9.2:

t =

(<X

> −<X









−1)s

+(N

−1)s

−2







(9.2)

This is just a generalized version of Equation 9.1. In the special case where variances are

equal, the denominator of Equation 9.2 simplifies to:







(9.3)

and when sample sizes are also equal, this simplifies further to:







(9.4)

as in Equation 9.1.

For the natural logs of jaw centroid sizes in Table 9.1, the 34 females have a mean of

3.94 and a variance of 3.9 ×10

−4

, while the 24 males have a mean of 3.96 and a variance

of 2.4 ×10

−4

. Putting the sample sizes and variances into the denominator of Equation

9.2 yields a value of 0.0048. The difference between means is 0.02, so t =2.7. The degrees

of freedom are one less than the number of individuals, which is 57. With 57 degrees of

freedom, the probability that t could be greater than or equal to 2.7 is 0.0091, which is

usually considered statistically significant. Thus the difference between means is small, but

the variances are even smaller, and so we can infer that males and females in this squirrel

population do differ in jaw size.

The question of whether there is a significant difference between groups can also be

answered without computing the difference between means. Instead, the variance explained

by the categorical variable is compared to the variance it does not explain (which is the

basis of the term analysis of variance, or ANOVA). The ratio of these two variances

(explained divided by unexplained) is the test statistic F. Like t, F has a known probability

distribution for pairs of samples drawn from the same normal distribution. Consequently,

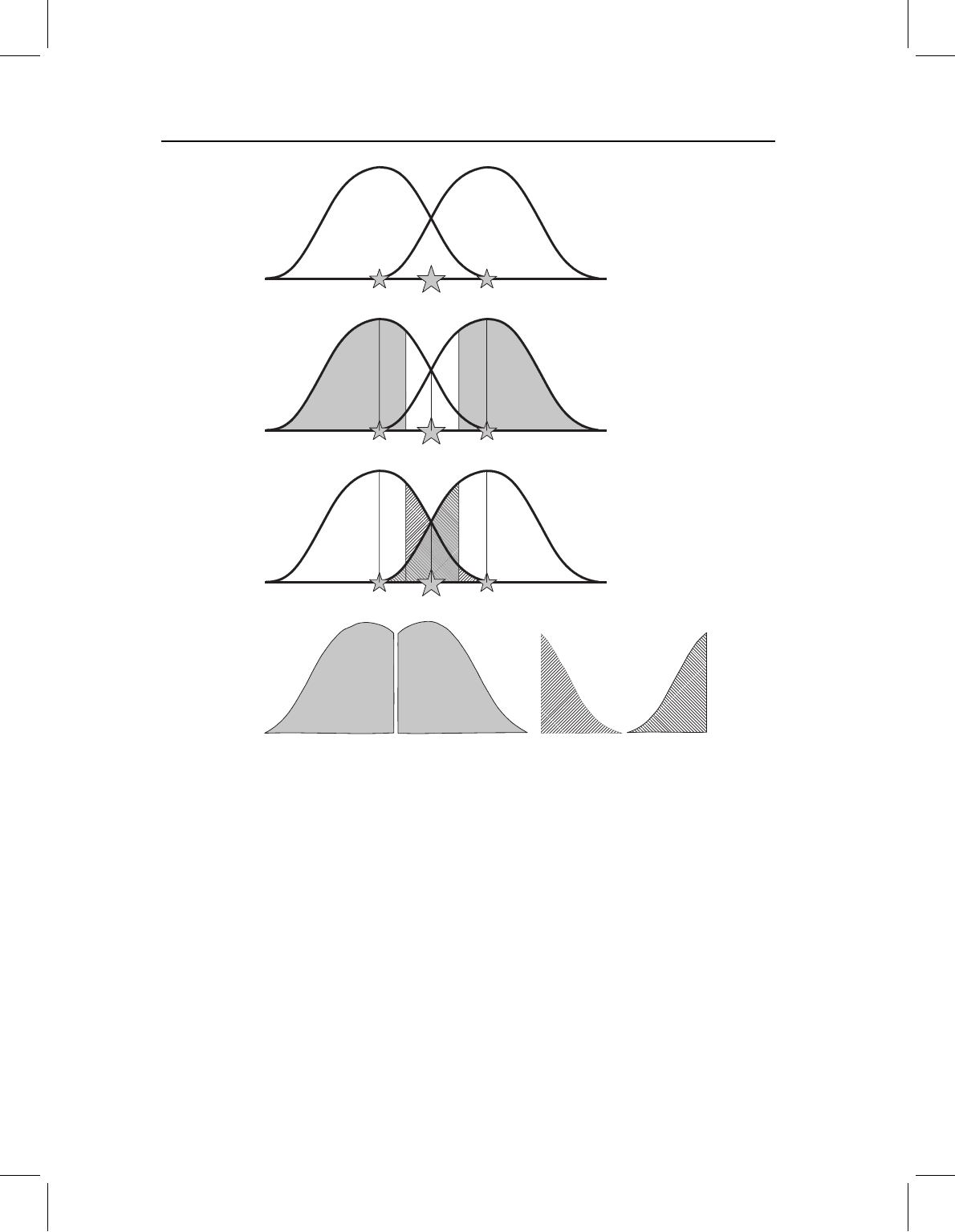
chap-09 4/6/2004 17: 25 page 213

MULTIVARIATE ANALYSIS OF VARIANCE 213

(D)

(C)

(B)

(A)

Figure 9.2 Graphic representation of ANOVA. Bell curves for two distributions are shown; the

small stars are the group means of the respective distributions; the large star is the grand mean.

(A) Both overlapping distributions are shown; (B) regions occupied by individuals closer to their

group mean than the grand mean are shaded; (C) regions occupied by individuals closer to the grand

mean than their group mean are indicated by diagonal hatching; (D) regions defined in B and C are

shown side-by-side to compare their areas.

the probability reported for the F-test is the probability of an equal or larger F-ratio for

two samples drawn randomly from the same distribution.

The logic underlying the F-test can also be explained graphically (Figure 9.2). We can

represent the variation in each sample as the area under a curve (Figure 9.2A). In each

group, some individuals are closer to their group mean than they are to the grand mean

(Figure 9.2B); other individuals are closer to the grand mean than they are to their group

mean (Figure 9.2C). The areas under the curves represented by these sets are shown in

Figure 9.2D. If the means are far apart, a large proportion of individuals will be closer to

their respective group means than to the grand mean, the value of F will be high, and the

classes will be judged significantly different.

chap-09 4/6/2004 17: 25 page 214

214 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

Computation of the F-ratio is complicated by the fact that the variance explained by

the categorical variable cannot be calculated directly from the data but must be computed

indirectly as the difference between the total variance and the variance that is not explained.

If this seems strangely convoluted, look again at Figure 9.2. We can compute the deviations

of each individual from the grand mean and use them to compute the total variance. We

can also compute the deviations of each individual from its respective group mean and

use them to compute the unexplained variance (the variance within the groups cannot be

attributed to the factor responsible for the difference between the groups). Subtracting the

unexplained variance from the total variance leaves the explained variance. For the natural

logs of jaw size, the sum of squared deviations from the grand mean is 0.0207. The sums

of squared deviations from the group means are 0.0055 for males and 0.0128 for females

for a total within-groups sum of squares of 0.0183. The difference between the total and

within-groups sums of squares is 0.0024; this is the between-groups sum of squares that

can be used to compute the variance explained by the categorical variable, sex.

Variance is the sum of the squared deviations divided by the number of degrees of free-

dom. The total degrees of freedom are N −1. The number of degrees of freedom attributed

to the categorical variable is G −1, where G is the number of groups or categories. (There

are fewer degrees of freedom than classes, because an individual that does not belong to the

first G −1 groups necessarily belongs to the last one.) Subtracting the degrees of freedom

allotted to the explained variance leaves N −G degrees of freedom for the unexplained vari-

ance. Returning to our example, N =58 and G =2. The explained variance (due to sexual

dimorphism) is 2.4 ×10

−3

/1, and the unexplained variance is 0.0183/56 =0.33 ×10

−3

The explained variance divided by the unexplained is 7.3. This F-ratio, with 1 and 57

degrees of freedom, has a p-value of 0.0091, which is identical to the p-value that was

obtained from the t-test. Thus, despite taking different approaches, the F-test and t-test

lead to the same result – the same conclusion regarding the significance of the difference

between the two groups.

It is important to remember that both the t-test and the F-test assume that the variances

within the groups are the same. Furthermore, both tests are asking whether samples as

different as yours could have been drawn from a single sample with a specific known

variance. Fortunately, both tests are fairly robust to violation of the assumption of equal

variances.

One simple trait, more than two groups

Because ANOVA compares variation within groups to variation between groups, it can

also be applied to analyses that examine more than two groups. For example, Table 9.2

illustrates an analysis of geographic variation in jaw size (the rows in the lower half of this

table are not in the order usually reported, but in an order that corresponds more closely

to the sequence of calculations). The categorical variable is geographic location, which

has three classes referring to three collecting areas (eastern Michigan, western Michigan,

and southern states). To test whether there is significant geographic variation in jaw size

(to test whether there are significant differences among the three populations), we follow

exactly the same procedure as for two groups. The sum of squared distances of individuals

from the grand mean is the total sum of squares (SSQ), and the sum of squared distances

of the individuals from their class means is the unexplained sum of squares. The difference

chap-09 4/6/2004 17: 25 page 215

MULTIVARIATE ANALYSIS OF VARIANCE 215

Table 9.2 ANOVA of jaw size with three groups

Western Eastern Southern All

Michigan Michigan States

N 69 23 27 119

Mean 3.95 3.96 4.01 3.97

SSQ 0.034 0.017 0.019 0.131

SSQ DF MSQ Fp

Total 0.131 118

Within-groups 0.070 116 <0.001

Between-groups 0.061 2 0.031 >50 <0.0001

between these quantities is the between-groups sum of squares. The variances are the mean

squares (MSQ), computed by dividing the sums of squares by the appropriate numbers of

degrees of freedom (DF). As in the previous example, these values are the number of groups

(localities) minus one, and the number of individuals minus the number of groups. Again,

the value of F is the ratio of the explained and unexplained variances. In this particular

example, the ratio is enormous (and imprecise due to rounding error) and the p-value is

miniscule, indicating that there is a highly significant difference in jaw size among the three

localities.

The conclusion that there is a difference among three or more classes does not imply

that the mean of each class is significantly different from the mean of every other class.

To determine whether that is the case, t-tests must be performed for all possible pair-wise

comparisons. In the squirrel example, there are three pairs of localities, and the three tests

indicate that the means of the two Michigan localities are not significantly different from

each other but both are significantly different from the mean of the southern locality.

When performing multiple unplanned tests to determine which groups are different,

it is important to remember that each additional test increases the chance that we might

falsely reject the null hypothesis that the two groups are not different. If we perform a test

and accept that the null hypothesis is rejected when the p-value is less than or equal to

0.05, we are also accepting the possibility that the test could be erroneous 5% of the time

(based on the model of a normal distribution). Each time the test is repeated, we run the

risk that the particular result will be erroneous, and increase the cumulative probability of

at least one erroneous result. The way to correct this problem is to require a lower p-value

before accepting that a test result supports rejection of the null hypothesis. One common

adjustment is the table-wide Bonferroni adjustment, in which the desired p-value is divided

by the number of tests. In the example above, we would require p < 0.05/3 for all tests.

Two or more categorical variables

The examples above have only a single categorical variable, but it is common to have

multiple categorical variables representing independent classifications of the specimens in

chap-09 4/6/2004 17: 25 page 216

216 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

the data set. In the data analyzed in the last example, there are male and female squirrels in

all three localities. This suggests that we should divide the variance in jaw shape into three

components: variance explained by sex, variance explained by geography, and variance

not explained by either sex or geography (Table 9.3). Two F-ratios are computed, one for

each categorical variable. As before, the variance explained by the categorical variable is

compared to the variance that is not explained, but now the unexplained variance is the

variance that is not explained by any categorical variable. This is a smaller quantity than

the variance that is not explained by that particular categorical variable.

The ANOVA can also be used to test whether sexual dimorphism differs among locali-

ties. In other words, we can test whether there is an interaction between the two categorical

variables. This requires computing the variance explained by a third categorical variable in

which the classes are defined by all possible combinations of the classes in the two original

categorical variables. This test can only be used if we have specimens representing all of

the possible classes in this new variable. If we had only males for one locality, we would

not be able to test for an interaction across all three localities (although we would be able

to test for an interaction over the two localities for which we do have both sexes). In the

jaw size example (Table 9.4), the interaction between sex and location explains very little

of the variation – albeit more than sex by itself. The lack of a significant interaction means

that sexual dimorphism is not significantly different among the three locations. (Sepa-

rate analyses on the three locations indicate that none of them exhibits significant sexual

dimorphism in jaw size.)

Notice that as we add explanatory variables to the model, the unexplained SSQ gets

progressively smaller as more of the total SSQ is attributed to the explanatory variables.

In addition, the unexplained SSQ is attributed to fewer degrees of freedom. Both of these

changes influence the F-ratios for the tests of specific hypotheses. In the squirrel jaw data,

the differences among localities are so large and the differences due to the other variables so

small that the decision to include additional variables did not alter conclusions. However,

Table 9.3 ANOVA of jaw size with two categorical variables

SSQ DF MSQ Fp

Locality 0.061 2 0.031 >50 <0.0001

Sex <0.001 1 <0.001 <0.15 >0.69

Unexplained 0.070 115 <0.001

Total 0.131 118

Table 9.4 ANOVA of jaw size with two categorical variables and their

interaction

SSQ DF MSQ Fp

Locality 0.060 2 0.031 >50 <0.0001

Sex <0.001 1 <0.001 <0.03 >0.86

Locality ×sex <0.001 2 <0.001 <0.11 >0.89

Unexplained 0.070 113 <0.001

Total 0.131 118

chap-09 4/6/2004 17: 25 page 217

MULTIVARIATE ANALYSIS OF VARIANCE 217

if the effects of sex or locality were marginal (if the F-ratios were close to the cut-off point

for an α of 0.05), then the conclusions could have been altered by the inclusion of the

interaction effect in the analysis. For this reason, all explanatory variables (including all of

their interaction terms) should be included in an ANOVA, and the explanatory variables

should be tested simultaneously, not one by one. If your data do not include specimens

for every possible combination of states of the categorical variables (e.g. you do not have

both sexes from every location), you should reduce the data set so that every possible

combination of the remaining states is included (e.g. include only the locations for which

you have both sexes). This will at least tell you whether there are interactions in that subset

of the data.

A categorical variable and a continuous variable

In some cases, one of the explanatory variables may be continuous rather than discontin-

uous. For example, we might anticipate that differences in shape between sexes are partly

due to differences in size between the sexes. Thus, we would want to account for the

differences in shape caused by differences in size so we can test for shape differences inde-

pendent of size differences. The continuous explanatory variable in this type of analysis is

called a “covariate.” The variance due to it is explained by the regression of the dependent

variable on the covariate. (Regression and related analyses, including alternative meth-

ods of accounting for variation explained by the covariate, are discussed in Chapter 10.)

Analyses of variance that include a covariate are called ANCOVA, or MANCOVA in the

multivariate case. Briefly, these methods use regression to control for the covariate. This is

done by estimating the expected value for the dependent variable(s) at a given value of the

covariate (usually, the Y-intercept). The value of the covariate does not matter when the

different groups have the same slope of the dependent variable on the covariate, because

their regression lines are then either parallel or coincident. If they are parallel, the groups

differ in shape even after adjusting for the covariate and they will differ by the same amount

and in the same direction over all possible values of the covariate. If the slopes are coinci-

dent, meaning the lines are actually the same, the difference between groups will be zero

for all values of the covariate. Thus, the first step of the analysis is to test for a significant

interaction between the covariate and the categorical variable. In Chapter 10 we present

a method for comparing shapes across groups when the interaction term is significant.

In Table 9.5 we show results for an analysis to determine whether there are differences

in jaw length among localities after accounting for variation in jaw length explained by

variation in jaw size (the covariate). This result shows a significant effect of locality on jaw

length, so there are differences in jaw length among localities that are independent of the

differences in jaw length that are associated with differences in jaw size. (The independence

Table 9.5 ANOVA of jaw length with jaw size as a covariate

SSQ DF MSQ Fp

Locality 0.003 2 0.002 >24 <0.0001

Jaw size 0.052 1 0.052 >740 <0.0001

Unexplained 0.008 115 <0.0001