Zehnder E. Lectures on Dynamical Systems: Hamiltonian Vector Fields and Symplectic Capacities
Подождите немного. Документ загружается.

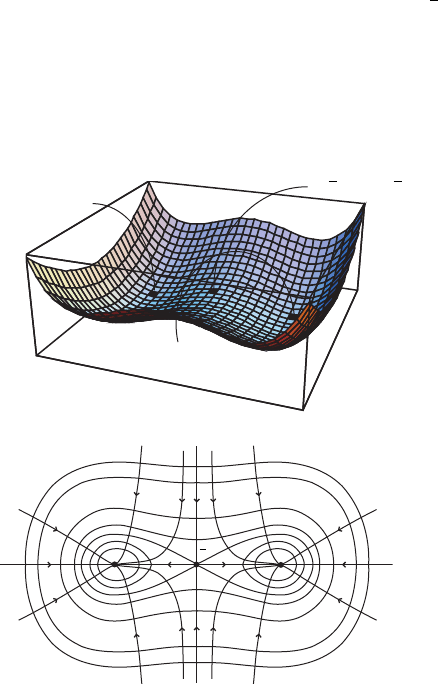
IV.3. Gradient systems 151
The critical points of V are the points in the set C D I.C/ Df.0; 0/; .
1
2
; 0/; .1; 0/g.
In view of Theorem IV.14 every solution converges to one of these points,
x t ! x
2 C as t !1:
This is illustrated in Figure IV.14.
01
1
2
.0; 0; V .0; 0//
.
1
2
;0;V.
1
2
; 0//
.1; 0; V .1; 0//
Figure IV.14. Graph of V and level lines with some solutions.
One can easily extend the qualitative concepts and results to the abstract situation
of continuous gradientlike flows on compact metric spaces .M; d / whose metric is
denoted by d .
Definition. A flow on a compact metric space M is a continuous mapping ' W R
M ! M satisfying
'.0; x/ D x;
'.t; '.s; x// D '.t C s; x/
for all x 2 M and for all t;s 2 R.
152 Chapter IV. Gradientlike flows
We note that the flow under consideration is, by assumption, complete. We
continue to use the notation
'.t; x/ D '
t
.x/ D x t:
In view of Proposition IV.1 the flows of vector fields on compact manifolds are
complete and hence are examples of flows on compact metric spaces.
Limit sets and orbits of the continuous flow are defined as in the case of smooth
flows of vector fields. Again, the orbits of a continuous flow partition the space
such that each point M is contained in precisely one orbit. Indeed, if x t D y s
then it follows that .x t/ D .y s/ and so, in view of the group structure of
the flow, x .t C / D y .s C /. This holds true for all in R and consequently
the orbits O.x/ and O.y/ must coincide.
Definition. A rest point of the flow ' (or constant orbit,orcritical point) is a point
x 2 M satisfying
x t D x for all t 2 R:
The following observation is important for the understanding of a rest point of
a continuous flow. If x t
j
D x for a sequence of non-vanishing real numbers
ft
j
j j 1g which converges to 0, then x t D x for all t 2 R, so that x is a rest
point of the flow. In order to prove this claim we first observe that, if t D nt
j
for
two integers n 2 Z and j , then x t D x in view of the group structure of the flow.
From this the claim follows, because the set fnt
j
j n 2 Z;j 2 Ng is dense in R
and the flow is continuous. If, for example, x t D x for t varying in an interval,
then x is a rest point of the flow.
Definition. We denote the set of rest points by
K ´fx 2 M j x is a rest point of the flow 'g:
The flow ' is called gradientlike, if there exists a continuous function V W M !
R, which decreases strictly along the non-constant orbits, i.e.,
V.x t/<V.x s/ for all t>s;and for all x … K:
Since M is compact, it follows by the arguments in Proposition IV.8,(ii) for
every point x 2 M that
xt ! !.x/; t !1;
xt ! !
.x/; t !1:
Arguing as in Theorem IV.10 we conclude that
!.x/ K and !
.x/ K;
and obtain the following result.
IV.3. Gradient systems 153
Theorem IV.15. Let ' be a gradientlike flow (with respect to V ) on a compact
metric space M . We assume that the set of rest points
K Dfx
1
;:::;x
N
g
is finite and label the points x
j
in such a way that
V.x
j
/ V.x
k
/ if j<k:
Then there exists for every x … K a pair j<kof indices satisfying
!.x/ D x
j
and !
.x/ D x
k
:
The invariant sets fx
1
g;:::;fx
N
gM having the properties as in the theorem
are said to constitute a Morse decomposition of the dynamical system .M; '/.
Definition. If a 2 R we denote by V
a
the sublevel set
V
a
´fx 2 M j V.x/ ag:
The set of constant orbits on the level a is denoted by
K
a
´ K \ V
1
.a/:
The real number a is called a critical value of the function V if K
a
¤;.
Theorem IV.16 (Deformation lemma). Let ' be a gradientlike flow (with respect
to the continuous function V ) on a compact metric space M and let U be an open
neighborhood of the constant orbits K
a
in M on the level a 2 R. Then there exists
an ">0such that the time 1 flow map '
1
satisfies
'
1
.V
aC"
n U/ V
a"
:
Special case: if K
a
D;and U D;, then
'
1
.V
aC"
/ V
a"
:
U
U
V
1
.a C "/
V
1
.a/
V
1
.a "/
Figure IV.15. The deformation lemma: outside of a neighborhood U of the rest points the
whole space flows downwards.
154 Chapter IV. Gradientlike flows
Proof. If X ´ V
1
.a/ n U , then X \ K
a
D;. Since the function V decreases
strictly along non-constant orbits, there exists for every x 2 X an open neighbor-
hood U
x
in M and a positive real number ı
x
>0such that
'
1
.U
x
/ V
aı
x
:
Because X is a compact set there exists a finite covering by such open sets, so
that
U
x
1
[[U
x
m
X:
Setting ı D minfı
x
1
;:::ı
x
m
g, it follows for " ı that
'
1
.U
x
1
[[U
x
m
/ V
a"
:
The set O ´ U [ U
x
1
[[U
x
m
is an open neighborhood of V
1
.a/.
Claim. If ">0is small enough, then V
1
.Œa "; a C "/ O:
Postponing the proof of the claim, we first finish the proof of the theorem. From
V
aC"
D V
a"
[ V
1
.Œa "; a C "/ V
a"
[ O
together with O n U U
x
1
[[U
x
m
it follows that
V
aC"
n U V
a"
[ U
x
1
[[U
x
m
;
and therefore
'
1
.V
aC"
n U/ '
1
.V
a"
/ [ '
1
.U
x
1
[[U
x
m
/ V
a"
;
as stated in the theorem and it remains to prove the claim.
Proof of the claim Arguing indirectly we assume that for every ">0there exists a
point x
"
2 V
1
.Œa "; a C"/ \O
c
. Hence, taking a sequence "
n
! 0 we find, in
view of the compactness of M and the fact that the set O
c
is closed, a sequence x
n
converging to x
2 O
c
. The continuity of V implies V.x
/ D lim
n!1
V.x
n
/ D a
and hence x
2 V
1
.a/, so that x
2 O
c
\ V
1
.a/, which is in contradiction to
V
1
.a/ O. The claim and therefore also the theorem are proved.
Index functions are a very useful tool in the search for rest points of a gradientlike
flow on a metric space. In order to define them we first recall the concept of a
deformation.
A deformation of a subset A of M is a continuous map f W A ! M which is
homotopic to the inclusion map A,! M . In other words, there exists a continuous
map F W Œ0; 1A ! M (a homotopy) satisfying F .0; x/ D x and F .1; x/ D f.x/
for all x 2 A.
IV.3. Gradient systems 155
Definition. An index function on the compact metric space M associates with
every subset A of M a non-negative integer in N [f0g,
A M 7! .A/ 2 N [f0g;
such that the following properties for subsets A; B M hold true.
(i) Monotonicity: A B H) .A/ .B/.
(ii) Subadditivity: .A [ B/ .A/ C .B/.
(iii) .;/ D 0.
(iv) Normalization: .fxg/ D 1 for every point x 2 M .
(v) Outer regularity : Every subset A M possesses an open neighborhood
U A such that .A/ D .U/.
(vi) Deformation monotonicity: If A M is a closed set and if f W A ! M is a
deformation of A
, then .A/ .f .A//.
If is an index function on M and if f W A ! M is a deformation of A satisfying
f .A/ D B and B A, then .B/ .A/ in view of the monotonicity of the index
function. On the other hand, by the deformation monotonicity, .A/ .B/ and
therefore .A/ D .B/. In particular, if B M is a deformation retract of M ,
then .B/ D .M/.
Theorem IV.17 (Lusternik–Schnirelman). Let M be a compact metric space and
assume that an index function on M exists. Then the number #K of rest points
of a gradientlike flow ' on M is estimated from below by
#K .M/:
Proof. We assume that ' is a gradientlike flow with respect to the continuous
function V .If#K D1, there is nothing to prove, and hence we assume #K<1.
We define the real numbers c
k
for 1 k .M/ by
c
k
´ inf
AM
.A/k
sup
x2A
V.x/
:
If we take a smaller k, the infimum is taken over a larger set and hence the numbers
c
k
are ordered according to
c
1
c
2
c
.M/
:
In view of the definition of an infimum there exists for every ">0a subset
A M such that .A/ k and
sup
x2A
V.x/<c
k
C ":
156 Chapter IV. Gradientlike flows
Therefore,
A V
c
k
C"
Dfx 2 M j V.x/ c
k
C "g:
From the monotonicity of the index function it therefore follows that
k .A/ .V
c
k
C"
/:
Moreover, .V
c
k
"
/<k, because otherwise we would arrive at the contradiction
c
k
D inf
AM
.A/k
sup
x2A
V.x/
sup
x2V
c
k
"
V.x/ c
k
":
Hence,
./.V
c
k
C"
/ k>.V
c
k
"
/ for all 1 k .M/; ">0:
Claim. On every level c
k
there exists a rest point, so that
V
1
.c
k
/ \ K ¤;:
Proof of the claim. Arguing by contradiction we assume that K
c
k
D V
1
.c
k
/ \
K D;. In view of the special case of the deformation lemma we find a small
positive number " such that
'
1
.V
c
k
C"
/ V
c
k
"
:
Since '
1
is a deformation (taking the flow ' as a homotopy), the deformation
monotonicity of leads to the estimate
.V
c
k
C"
/ .'
1
.V
c
k
C"
// .V
c
k
"
/;
where the second inequality follows from the monotonicity of the index . This
estimate, however, contradicts the estimate .V
c
k
C"
/>.V
c
k
"
/ in ./ and the
claim is proved.
If c
1
<c
2
< <c
.M/
, there exist, therefore, at least .M/ rest points, as
claimed in the theorem. If the levels are not different from each other, there still
exist sufficiently many rest points, as we will verify next.
Claim. If c
k
D c
kC1
DDc
kCr
for a positive integer r>0and an integer k,
then there exist at least r C 1 rest points on this level,
#K
c
k
D #
V
1
.c
k
/ \ K
r C 1:
IV.3. Gradient systems 157
Proof of the claim. Let K
c
k
Dfx
1
;:::;x
l
g be the rest points in V
1
.c
k
/. From
the subadditivity properties of the index function we conclude .fx
1
;:::;x
l
g/ l.
./ Due to the outer regularity of the index there exists an open neighborhood
U of the set fx
1
;:::;x
l
gsatisfying .U / l. According to the deformation lemma
(Theorem IV.16) we find a positive " such that
'
1
.V
c
k
C"
n U/ V
c
k
"
:
In view of the deformation monotonicity and of the estimate in ./ we therefore
obtain
./.V
c
k
C"
n U/ .'
1
.V
c
k
C"
n U// .V
c
k
"
/<k:
From the assumption c
k
D c
kCr
we conclude, using the subadditivity of the index
function and the estimate in ./,
.V
c
k
C"
n U/C .U/ D .V
c
kCr
C"
n U/C .U/
ŒV
c
kCr
C"
n U[ U
.V
c
kCr
C"
/
k C r:
Using ./ it follows that
.U/ k C r .V
c
k
C"
n U/>r;
hence l .U/ r C 1, and the claim is proved. The proof of Theorem IV.17 is
complete.
Remark. The critical levels c
k
are also characterized by
c
k
D inffc 2 R j .V
c
/ kg:
This is a consequence of the estimate in ./.
The Lusternik–Schnirelman category. An example of an index function on topo-
logical spaces is the Lusternik–Schnirelman category which is a strong tool for the
search of solutions of variational problems. It is a topological invariant defined
as the smallest cardinality of closed contractible subsets covering the spaces. We
shall formulate the definition in metric spaces and start with the notion of a con-
tractible set.
Definition. Let M be a metric space. A subset A M is called contractible in
M , if the inclusion mapping A,! M is nullhomotopic in M . In other words,
there exists a continuous map F W Œ0; 1 A ! M satisfying F .0; x/ D x and
F .1; x/ y
2 M for all x 2 A.
158 Chapter IV. Gradientlike flows
We point out that we do not require that the homotopy F is a map of Œ0; 1 A
into A (instead of into M ).
Definition. Let M be a metric space and A M a subset. The Lusternik–
Schnirelman category of A in M , denoted by
cat
M
.A/ 2 N [f0g[ f1g;
is defined as follows. We set cat
M
.A/ D k 2 N [f0g if there exist k closed, in M
contractible sets A
j
M which cover A, so that
A A
1
[[A
k
;
and if k is the smallest integer having this property. If such a finite covering does
not exist, we set cat
M
.A/ D1.
Since the properties being closed and contractible are preserved under homeo-
morphisms, the category is a topological invariant.
Proposition IV.18. Let M be a metric space. The Lusternik–Schnirelman category
cat
M
has the following properties for subsets A and B of M .
(i) Monotonicity: A B H) cat
M
.A/ cat
M
.B/.
(ii) Subadditivity: cat
M
.A [ B/ cat
M
.A/ C cat
M
.B/.
(iii) cat
M
.;/ D 0.
(iv) Normalization: cat
M
.fxg/ D 1, x 2 M .
(v) cat
M
.A/ D cat
M
.
x
A/.
(vi) Deformation monotonicity: If the subset A M is closed and if f W A ! M
is a deformation of A, then cat
M
.A/ cat
M
.f .A//.
It follows, in particular, that cat
M
.A/ D cat
M
.B/ if A is a deformation retract of the
subset B. The Lusternik–Schnirelman category cat
M
has, with the exception of the
outer regularity, all the properties of an index function, provided cat
M
.M / < 1.
Proof. All the statements except the deformation monotonicity follow directly from
the definition. In order to verify the deformation monotonicity we consider the
deformation f W A ! M of the closed subset A. If cat
M
.f .A// D1there is
nothing to prove and we assume that cat
M
.f .A// D k<1. Then there exist k
closed, in M contractible sets B
j
such that
f .A/ B
1
[[B
k
:
The sets A
j
´ f
1
.B
j
/ A are, due to the continuity of f , closed in A D
x
A
and therefore also closed in M . Since f j
A
j
W A
j
! B
j
is a deformation in B
j
and since B
j
is contractible in M , also the set A
j
is contractible in M . From
A A
1
[[A
k
it follows that cat
M
.A/ k D cat
M
.f .A// and the proof of
the proposition is finished.
IV.3. Gradient systems 159
We now restrict the class of metric spaces under consideration and require that
the metric space M is semilocally contractible. In other words we require that every
point x 2 M possesses an open neighborhood U whose closure
x
U is contractible
in M . Every normed vector space, as for example R
n
, possesses this property,
because we can just take an open ball around x for the neighborhood U . Since it is
locally homeomorphic to a normed vector space, a metric manifold is semilocally
contractible.
If A M is a compact subset, we choose for every point x 2 A a neighborhood
U
x
such that its closure
x
U
x
is contractible in M . There exists a finite subcovering
satisfying
A U
x
1
[[U
x
N
x
U
x
1
[[
x
U
x
N
;
and we conclude from the definition of cat
M
that cat
M
.A/ N . Therefore,
compact subsets A of a semilocally contractible space M have a finite category,
cat
M
.A/ < 1.
In particular, cat
M
is finite on a compact manifold M .
The Lusternik–Schnirelman category of a space is in general not easy to com-
pute. Here are some well-known examples.
Examples. (1) If V is a normed vector space, then f0g is a deformation retract of
V , and hence
cat
V
.V / D 1:
(2) If A Dfx
1
;:::;x
n
g is a non-empty finite subset of a path-connected space
M , then
cat
M
.A/ D cat
M
.fx
k
g/ D 1:
(3) We consider the n-dimensional sphere S
n
for n 1 equipped with the metric
induced from R
nC1
. We choose a point x
2 S
n
and a small open ball U centered
at x
in the sphere. Then
x
U is contractible to the point fx
g and we conclude from
property (v) that
cat
S
n
.U / D cat
S
n
.
x
U/ D cat
S
n
.fx
g/ D 1:
The complement U
c
D S
n
nU is also contractible on the sphere S
n
and hence has
also the category equal to 1. In view of the subadditivity, cat
S
n
.S
n
/ cat
S
n
.U / C
cat
S
n
.U
c
/ D 2 and since S
n
is not contractible in S
n
we find
cat
S
n
.S
n
/ D 2; n 1:
(4) In contrast, the unit sphere S
1
Dfx 2 V jkxkD1g in an infinite-
dimensional normed vector space V is a retract of V (for a proof we refer to p. 66
in [26] by K. Deimling), from which it follows that S
1
is contractible in itself, so
that
cat
S
1
.S
1
/ D 1:

160 Chapter IV. Gradientlike flows
(5) The Lusternik–Schnirelman category of the n-dimensional torus T
n
is equal
to
cat
T
n
.T
n
/ D n C 1; n 1;
The proof can be found in [101] by J. Schwartz and in [22] by O. Cornea et al.
Theorem IV.19 (Lusternik–Schnirelman). If '
t
is a gradientlike flow on a compact
manifold M (or more generally, on a semilocally contractible and compact metric
space M ), then the number of its rest points K is estimated from below by
#K cat
M
.M /:
Proof [Theorem IV.17]. In view of Proposition IV.18 we can take over almost the
complete proof of Theorem IV.17 for the function cat
M
instead of the index function
. We have used the outer regularity only in the proof of the second claim in the
proof of Theorem IV.17 and have marked this passage with ./. Instead, we now
use the semilocal contractibility in order to verify that the finite set of rest points
fx
1
;:::;x
l
gM possesses an open neighborhood U satisfying cat
M
.U / l.
We choose open neighborhoods U
i
of x
i
in such a way that U
i
is contractible
in M . Then the union U D U
1
[[U
l
is an open neighborhood of fx
1
;:::;x
l
g
satisfying U
U
1
[[U
l
so that cat
M
.U / l. The rest of the proof is identical
with the proof of Theorem IV.17.
Remark. If the metric space M is a manifold then cat
M
is regular from the outside.
If, moreover, M is a compact manifold, then
cat
M
.M / dim M C 1<1
is finite, so that cat
M
is an index function. More generally, the inequality
cat
M
.A/ dim A C 1
holds true for every compact subset of a (Hilbert-)manifold M , where dim A is
the covering dimension from topology. With the differential topological concept
of the cuplength the following very useful estimate of the Lusternik–Schnirelman
category holds true,
cuplength M C 1 cat
M
.M /:
For proofs we refer to the books [22] by O. Cornea et al., [26] by K. Deimling and
[101] by J. Schwartz.
Exercise. On the torus T
2
D R
2
=Z
2
the function
V W T
2
! R; V .x; y/ D sin.x/ sin.y/ sin..x C y//
has exactly three critical points, namely the minimum, the maximum and a degen-
erate saddle point which is a so-called monkey saddle.
