Zehnder E. Lectures on Dynamical Systems: Hamiltonian Vector Fields and Symplectic Capacities

Подождите немного. Документ загружается.

IV.1. Flow of a vector ﬁeld, recollections from ODE 131

it follows from the assumption that u.t/  a.t/ C v.t/. Therefore,

Pv.t/  b.t/Œa.t / C v.t/:

Hence, using P Db.t/.t/ one obtains



.t/v.t/



 a.t/b.t/.t/:

Integrating this inequality from 0 to t and observing that v.0/ D 0 one arrives at

the estimate

.t/v.t/ 

a.s/b.s/.s/ ds:

In view of the monotonicity of the function a we get .t/v.t/  a.t/

b.s/.s/ ds

and hence,

u.t/.t/  Œa.t/ C v.t /.t/

 a.t/



.t/ C

b.s/.s/ ds



The integration of P.t/ Db.t/.t/ together with .0/ D 1 results in

b.s/.s/ ds D 1  .t/:

Hence, it follows from the above estimate that, indeed, u.t/.t/  a.t/ and the

lemma is proved. 

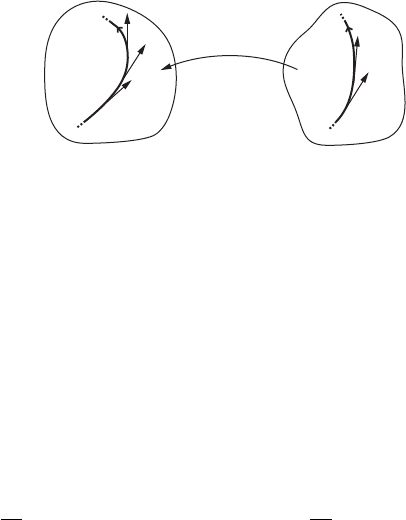
We next recall the concept of equivalent vector ﬁelds. We consider a diffeomor-

phism u W 

!  between the open sets 

;  R

.IfX is a vector ﬁeld on

 and x.t/ D '

.x/ a solution of the equation Px D X.x/, then we can associate

with the differentiable curve x.t/ in  the differentiable curve y.t/ in 

deﬁned

by x.t/ D u.y.t// or

y.t/ D u

1

.x.t//:

The curve y.t/ is a solution of a vector ﬁeld on 

. Indeed, from

X.u.y.t/// D X.x.t// DPx.t/ D du.y.t // Py.t/;

it follows that the curve y.t/ solves the equation Py.t/ D Œdu.y.t//

1

X.u.y.t///.

Therefore, the curve y.t/ is a solution of the vector ﬁeld Y deﬁned by

Y.y/ D Œdu.y/

1

X.u.y//; y 2 

The vector ﬁeld

Y D .du/

1

X B u μ u



is called the transformed vector ﬁeld or the pull-back of the vector ﬁeld X under

the diffeomorphism u.

132 Chapter IV. Gradientlike ﬂows

Deﬁnition. The vector ﬁeld X on  and the vector ﬁeld Y on 

are called

equivalent, if there exists a diffeomorphism uW 

!  satisfying

du.y/Y .y/ D X.u.y//; y 2 

;

or equivalently,

Y.y/ D .du.y//

1

X.u.y// D .u



X/.y/; y 2 

Two vector ﬁelds are equivalent, if and only if their local ﬂows are conjugated.



y.t/

x.t/

Figure IV.2. Two equivalent vector ﬁelds with ﬂows.

Proposition IV.5. Let u W 

!  be a diffeomorphism. If X is a vector ﬁeld

on  having the ﬂow '

and Y a vector ﬁeld on 

having the ﬂow

, then the

following two statements are equivalent.

(i) du.y/Y .y/ D X.u.y// for all y 2 

;

(ii) u B

.y/ D '

B u.y/ on the domains of deﬁnition.

Proof [Deﬁnition and uniqueness of the ﬂow]. (ii) H)(i): Differentiating the con-

jugacy identity in t at the time t D 0, one ﬁnds, using the chain rule,

du.

.y//

.y/ D du.

.y//Y .

.y// D

.u.y// D X.'

.u.y//:

Due to

.y/ D y and '

.u.y// D u.y/, the identity du.y/Y .y/ D X.u.y//

follows for t D 0.

(i) H)(ii): Introducing the family of diffeomorphisms

.y/ ´ u

1

Bu.y/,

we obtain the identity

./uB

.y/ D '

B u.y/:

We want to show that

is the ﬂow of Y . In view of the uniqueness it suf-

ﬁces to verify that

.y/ D y (this follows immediately from '

D Id) and that

IV.1. Flow of a vector ﬁeld, recollections from ODE 133

.y/ D Y.

.y// for t 2 I

. By differentiating the equation ./ in t we obtain

by the chain rule

du.

.y//

.y/ D

.u.y//

D X.'

.u.y///

D X.u.

.y///;

and using the assumption (i) the desired equation

.y/ D Y.

.y// follows.



Instead of going immediately after the solutions of a given vector ﬁeld, it is often

more advisable to ﬁrst transform the vector ﬁeld into a simple form from which the

solutions can be read off easily. This is illustrated by the following local result.

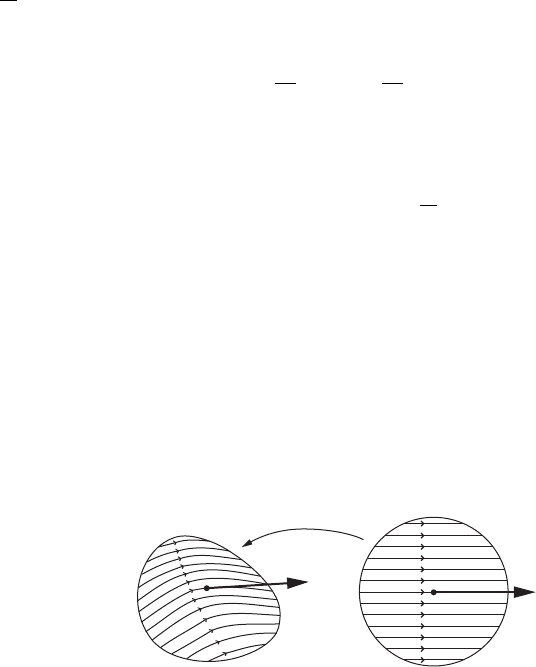
Theorem IV.6 (Local straightening out theorem). Let x



be a regular point of

the C

vector ﬁeld X , that is, X.x



/ ¤ 0. Then, there exists a neighborhood

U of x



on which the vector ﬁeld X is equivalent to the constant vector ﬁeld

Y.y/ D e

D .1;0;:::;0/.

X.x



Y.u

1



// D e

Figure IV.3. The local straightening out theorem.

Hence, there exists an open set U

and a diffeomorphism u W U

! U satisfying

du.y/e

D X.u.y// for y 2 U

. The ﬂow of the constant vector ﬁeld Y is

obviously equal to

.y/ D y C te

, so that the local ﬂow '

of X near x



represented by

.u.y// D u.y C te

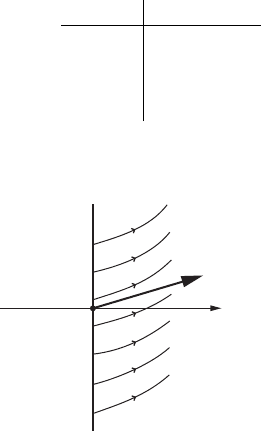
Proof of the theorem [Inverse function theorem]. By translation, we can assume

that x



D 0 is the origin. Since X.0/ ¤ 0, we can, after renumbering of the

coordinates, assume that

hX.0/; e

iDX

.0/ ¤ 0:

134 Chapter IV. Gradientlike ﬂows

Using the local ﬂow '

of the vector ﬁeld X near x



D 0 we deﬁne the map

uW R

! R

in the neighborhood of 0 by

y D .y

;:::;y

/ 7! u.y/ ´ '

.0; y

;:::;y

Then u.0/ D '

.0/ D 0 and

du.0/ D

.0/ 0 ::: 0

.0/ 1

.0/

This follows directly from the deﬁnition of the ﬂow of the vector ﬁeld X. Hence,

det du.0/ D X

.0/ ¤ 0 and in view of the inverse function theorem the map u is

D 0g

X.0/

Figure IV.4. Geometrically, the plane fy

D 0g is locally a transversal section of X.

a local diffeomorphism u W U

! u.U

/ μ U leaving the origin ﬁxed, where U

is an open neighborhood of the origin. We deﬁne the constant vector ﬁeld Y on U

by Y.y/ D e

. Its ﬂow is equal to

.y/ D y C te

and one computes,

u B

.y/ D u.y

C t;y

;:::;y

D '

.0; y

;:::;y

D '

B '

.0; y

;:::;y

D '

B u.y/:

Consequently, the ﬂows are conjugated and the theorem follows from Proposi-

tion IV.5. 

Corollary IV.7. All the vector ﬁelds of the same dimension are equivalent locally

in the neighborhood of regular points. Near a regular point, there exist no local

invariants.

IV.1. Flow of a vector ﬁeld, recollections from ODE 135

The dynamics near a regular point is clearly not interesting and we introduce

next the singular points where the vector ﬁeld vanishes.

Deﬁnition. A point x



is called a singular point (or equilibrium point or rest point)

of a vector ﬁeld X ,ifX.x



/ D 0.

The solution of a vector ﬁeld through the singular point x



satisﬁes '



/ D x



for all t. At a singular point we shall encounter local invariants of the vector ﬁeld.

We assume that X and Y are equivalent vector ﬁelds, so that

du.y/Y .y/ D X.u.y//

with a local diffeomorphism u.Ifx



D u.y



/ is a singular point of X, then

X.x



/ D 0 () Y.y



/ D 0:

We linearize the vector ﬁelds at the corresponding singularities. Differentiating the

previous identity in the variable y at the point y D y



one obtains the equation

du.y



/dY.y



/ D dX.x



/ du.y



or equivalently,

dY.y



/ D Œdu.y



/

1

dX.x



/du.y



Hence, the two linear maps dY.y



/ and dX.x



/ belonging to L.R

/ are equivalent.

Consequently, they possess the same eigenvalues, and, more generally, they have

the same Jordan normal forms. These data are the linear invariants of the vector

ﬁeld at the singular point.

Remark (Reparametrization of the time). We consider the vector ﬁeld X and denote

its ﬂow by '

. The curve t 7! '

.x/ is a solution, hence a parameterized orbit. We

can reparametrize this orbit as a solution of the rescaled vector ﬁeld Y deﬁned by

Y.x/ D %.x/X.x/; x 2 R

;

where % W R

! R is a positive C

function. We claim that the ﬂow

of this

vector ﬁeld Y satisﬁes

s.t;x/

.x/ D '

.x/;

where t 7! s.t; x/ is the strictly increasing function from R into R,deﬁned as the

unique solution of the Cauchy initial value problem

.x//

>0;

s.0; x/ D 0;

in which x enters as a parameter.

136 Chapter IV. Gradientlike ﬂows

Proof. In order to prove the claim, we verify that the curve t 7!

s.t;x/

.x/ solves

the Cauchy initial value problem for the vector ﬁeld X with the initial condition

s.0;x/

.x/ D

.x/ D x:

Differentiating in time t and using the chain rule, we compute

s.t;x/

.x/ D

.x/

.t; x/

D Y.

.x//

.t; x/

D %.

.x//X.

.x//

.t; x/

D %.

.x//X.

.x//

D X.

s.t;x/

.x//:

The uniqueness of the ﬂow implies indeed that '

.x/ D

.x/ with s D s.t; x/ as

claimed. 

From

.t; x/ D

.x//

%.'

.x//

we obtain in view of s.0; x/ D 0, the following transformation formula for the time

parameter,

s.t;x/ D

d

%.'



.x//

Example. If %.x/ D >0, then s.t; x/ D



IV.2 Limit sets, attractors and Lyapunov functions

Where do the solutions come from and where do they go to? In order to study the

asymptotic behavior as jtj!1, it is useful to ﬁrst introduce the concept of a limit

set of an orbit. To do so, we consider the ﬂow '

of the vector ﬁeld X in R

and

abbreviate it as

.x/ D x  t; t 2 I

We recall that the differentiable mapping .t; x/ 7! x  t on its domain of deﬁnition

U  R  R

into R

satisﬁes the properties

x  0 D x; x 2 R

;

.x  t/  s D x  .t C s/; s;t;t C s 2 I

;

IV.2. Limit sets, attractors and Lyapunov functions 137

where



 t



.x/; t

.x/



 R

is the maximal interval of deﬁnition of the orbit with initial condition x. We shall

denote the unparametrized orbits of the ﬂow as the sets

.x/ Dfx  t j 0  t<t

.x/g;



.x/ Dfx  t j t



.x/<t 0g;

O.x/ Dfx  t j t



.x/<t<t

.x/g:

Deﬁnition. If t

.x/ D1, the !-limit set of the point x is the set

!.x/ ´fy 2 R

j there exists a sequence t

!1satisfying x  t

! yg:

If t



.x/ D1, we deﬁne



.x/ ´fy 2 R

j there exists a sequence t

!1satisfying x  .t

/ ! yg:

The limit sets can be empty. The limit sets can equivalently be deﬁned by

!.x/ D

s>0

.x  s/;



.x/ D

s<0



.x  s/

from which one concludes that !.x/ and !



.x/ are closed sets. In order to verify

the above representations of the limit sets we assume that y 2

.x  s/ for every

s>0. Therefore, there exists for every positive integer n a real number t.n/>n,

such that the distance between x  t.n/ and y is smaller than n

1

. The sequence

t.n/ satisﬁes lim t.n/ D1and lim x  t.n/ D y, so that y is an element of !.x/.

Conversely, if y is an element of !.x/, then there exists a sequence t

satisfying x t

! y.Ifs>0is given, then x t

2 O

.x s/ for sufﬁciently large

integers n and hence y D lim x  t

2 O

.x  s/. This holds true for every s>0.

Example. On R

we study the differential equations

D x

C x

.1  r

Dx

C x

.1  r

where r

D x

. In order to decouple this coupled system of differential equa-

tions we introduce the polar coordinates .x

/ D .r cos #; r sin #/ and obtain by

means of the transformation formula for vector ﬁelds the two decoupled equations

Pr D r.1  r

# D1:

138 Chapter IV. Gradientlike ﬂows

Figure IV.5. The vector ﬁeld . Px

; Px

/ from the example, shown with the circle S

(left), and

some solutions (right).

Clearly, the solutions of the second equation are the functions #.t/ Dt C#.0/.

The ﬁrst equation can, of course, also be solved explicitly by a formula for the

solutions r.t/. This, however, is not necessary because the qualitative behavior of

the solutions on the positive real axis are obvious. Namely, the points r D 0 and

r D 1 are the rest points and all the solutions starting in the complements of these

rest points have to converge to the rest point r D 1 as t !1. In backward time

the solutions starting at points r smaller than 1 converge to the rest point r D 0

while those starting at points larger than 1 diverge to inﬁnity.

Therefore the limit sets of the solutions x.t/ in R

are the sets

!.0/ Df0g;

!.x/ D S

;x2 R

nf0g;



.x/ D;; jxj >1;



.x/ D S

; jxjD1;



.x/ Df0g; jxj <1:

Here S

is the unit circle centered at the origin.

Proposition IV.8 (Properties of the limit sets). The !-limit set !.x/ is invariant

under the ﬂow so that !.x/  t  !.x/ for every t.

If the closure

.x/ of the orbit is compact (and hence t

.x/ D1by Propo-

sition IV.1), the limit sets have the following properties.

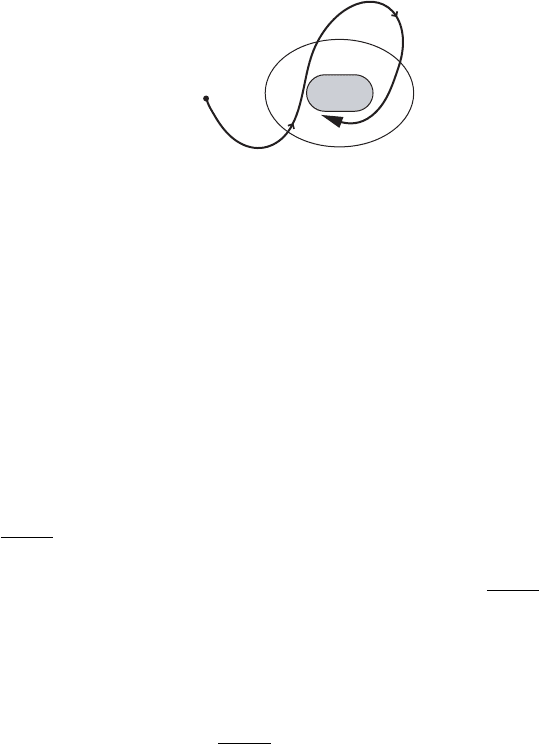
(i) !.x/ is compact and not empty,

(ii) x  t ! !.x/ as t !1,

IV.2. Limit sets, attractors and Lyapunov functions 139

!.x/

Figure IV.6. Proposition IV.8 (ii).

(iii) !.x/ is a connected set.

The limit set !



.x/ has analogous properties as the time tends to minus inﬁnity.

Proof. If y 2 !.x/, there exists a sequence t

!1satisfying x  t

! y and

using the continuity of the ﬂow we conclude for every real number t,

y  t D



lim

n!1

x  t



 t D lim

n!1

x  .t

C t/:

Since t

C t !1as n !1we ﬁnd y  t 2 !.x/, so that the limit set is indeed

invariant under the ﬂow.

(i)We take a sequence t

!1. Then the sequence .xt

n1

lies in the compact

set

.x/, so that there exists a convergent subsequence whose limit belongs to

!.x/, in view of the deﬁnition of a limit set. Consequently, the limit set !.x/ is not

empty. Since !.x/ is closed and contained in the compact set

.x/, the limit set

!.x/ is compact.

(ii) We shall prove that for every sequence t

!1and for every open neigh-

borhood U of !.x/ there exists an integer n

, satisfying x t

2 U for all n  n

Arguing by contradiction we assume that x  t does not converge to !.x/. Then

there exists an open neighborhood U of !.x/ and a sequence t

!1satisfying

x  t

… U for all n. Since O

.x/ \ U

is compact, there exists a convergent

subsequence x  t

! y 2 U

. Its limit satisﬁes y 2 !.x/ \ U

, in contradiction

to the assumption U  !.x/.

(iii) In order to prove the statement in (iii), we argue again by contradiction and

assume the existence of two closed sets !

¤;satisfying !.x/ D !

[ !

and !

D;. With !.x/ also the sets !

and !

are compact. Therefore, there

exist open sets U

 R

satisfying

 U

\ U

D;:

The set U ´ U

[ U

is an open neighborhood of !.x/. In view of (ii),

x  t 2 U; t  t

140 Chapter IV. Gradientlike ﬂows

Figure IV.7. Proposition IV.8 (iii).

for some time t

2 R. Since the interval Œt

; 1/ is connected and the ﬂow con-

tinuous, the image set fx  t j t

 t<1g under the ﬂow is connected. In view

of the deﬁnition of U this set must therefore lie completely in one of the two open

sets, let us say in U

. Consequently, there exists no sequence t

!1, for which

x  t

converges to a point in !

 U

and since !

 !.x/ we conclude that

D;, in contradiction to the assumption. We have veriﬁed that the limit set !.x/

is connected and the proposition is proved. 

Deﬁnition. A point x 2 R

is attracted by a subset M  R

,ift

.x/ D1and

x  t ! M for t !1:

The domain of attraction of M is the set of all points attracted by M and is

denoted by A.M /. A closed set M is called an attractor,ifA.M / is a neighborhood

of M .

Lyapunov functions can be a useful tool to localize limit sets and to ﬁnd attrac-

tors.

Deﬁnition. A continuous function V W R

! R is called a Lyapunov function of

the ﬂow, if it decreases along every orbit, so that for every x 2 R

V.x  t/  V.x  s/ for all t  s:

The derivative of a Lyapunov function along the ﬂow is, by deﬁnition, the function

V.x/´ lim

t&0

ŒV .x  t/  V .x/:

Here we made use of the well-known deﬁnition for a function ' W .a; b/ ! R,

lim

h&a

'.h/ ´ sup

a<tb

inf

a<h<t

'.h/

D lim

t&a

inf

a<h<t

'.h/

Clearly, a Lyapunov function satisﬁes 1 

V.x/ 0.