Zehnder E. Lectures on Dynamical Systems: Hamiltonian Vector Fields and Symplectic Capacities

Подождите немного. Документ загружается.

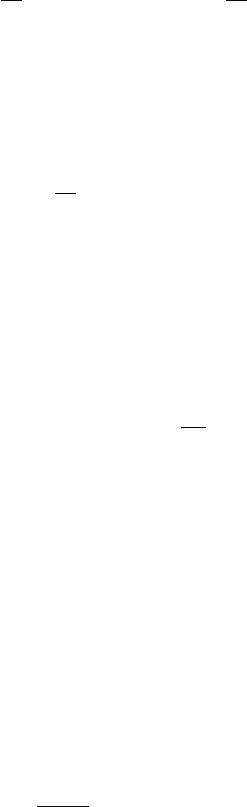
IV.2. Limit sets, attractors and Lyapunov functions 141

Example. If V W R

! R is any differentiable function and x  t D '

.x/ is the

ﬂow of the vector ﬁeld X , then by the chain rule and the deﬁnition of the ﬂow of a

vector ﬁeld,

V.'

.x// D dV.'

.x//

.x/

D dV.'

.x/ X.'

.x//

DhrV.'

.x//; X.'

.x//i:

The vector ﬁeld rV is the gradient of the function V with respect to the Euclidean

scalar product. Therefore,

V.x/D

V.'

.x//

tD0

DhrV .x/; X.x/i:

We will frequently make use of this calculation.

Lemma IV.9. Let X be a vector ﬁeld with ﬂow '

and let V W R

! R be a

differentiable function. Then V is a Lyapunov function of the ﬂow '

if and only if

hrV .x/; X.x/i0 for all x 2 R

Proof. If hrV .x/; X.x/i0 for all x 2 R

, then it follows for t  s that

V.'

.x//  V.'

.x// D

d

V.'



.x// d 

hrV.'



.x//; X.'



.x/id

 0;

so that V is a Lyapunov function. Conversely if V is a Lyapunov function, then

V.x/  0 and in view of the above calculation, hrV .x/; X.x/iD

V.x/  0,as

claimed. 

Theorem IV.10 (La Salle’s principle). We assume that V is a Lyapunov function

on the closed set M . Let O

.x/  M be an orbit whose limit set !.x/ ¤;is not

empty. Then

(i) !.x/  V

1

.˛/ for an ˛ 2 R, i.e., V j

!.x/

D const.,

(ii) !.x/ fy 2 M j

V.y/D 0g, i.e.,

V j

!.x/

D 0.

Proof. Clearly, !.x/ 

.x/ 

M D M . Since V.x  t/ is decreasing, there

exists the limit lim

t!1

V.xt/ D inf

t0

V.xt/ μ ˛ in R [f1g.Ify 2 !.x/,

there exists a sequence t

!1satisfying x  t

! y and the continuity of the

function V implies

lim

n!1

V.x  t

/ D V.y/ D ˛:

142 Chapter IV. Gradientlike ﬂows

In particular, ˛ 2 R. This holds true for every y 2 !.x/, so that V.y/ D ˛ for

all y 2 !.x/ and (i) is proved. Since !.x/ is invariant under the ﬂow in view of

Proposition IV.8, it follows for y 2 !.x/, that V.y  t/ D V.y/ D ˛ for all t and

consequently

V.y/D 0, as claimed in the theorem. 

Deﬁnition. The maximal invariant set of the subset M  R

is the set

I.M/ Dfx 2 M j x  t 2 M for all t in Rg:

Example. If 0 is a hyperbolic equilibrium point of a vector ﬁeld then there exists an

open neighborhood M whose maximal invariant subset consists of the equilibrium

point, so that I.M/ Df0g.

Proposition IV.11. Let V be a Lyapunov function on a closed set M and assume

that the orbit O

.x/  M has a compact closure O

.x/. Then for the set C deﬁned

C ´fy 2 M j

V.y/D 0g;

it holds true that

x  t ! I.C/; t !1:

If, in addition, the set M is positively invariant, so that M  t  M for all t  0,

and if

.x/ is compact for every x 2 M , then

M  A.I.C //:

Proof [Theorem IV.10]. Take x 2 M , then !.x/ ¤;due to Proposition IV.8.In

view of Theorem IV.10,

!.x/ fy 2 M j

V.y/D 0gDC:

Since !.x/ is invariant under the ﬂow (Proposition IV.8), we have !.x/  I.C/.

From x  t ! !.x/ as t !1we conclude x  t ! I.C/.

Finally, if the additional assumptions of Proposition IV.11 are satisﬁed, then

x t ! I.C/ for every x 2 M so that M  A.I.C //, as we wanted to prove. 

Proposition IV.12. Let V be a coercive Lyapunov function on R

, i.e., V.x/ !1

for jxj!1. Then the closure

.x/ of every orbit is compact, the set C ´

fy 2 M j

V.y/D 0g is not empty and the maximal invariant set I.C/ is a global

attractor,

A.I.C // D R

Proof. Since V is continuous, the sublevel set V

´fx 2 R

j V.x/  ag is

closed for every a 2 R.Ifa is sufﬁciently large, the set V

¤;is not empty. Due

to the coerciveness of the function V , the set V

is bounded and hence compact.If

x 2 V

, then V.x  t/  V.x/  a for every 0  t<t

.x/ so that t

.x/ D1,

IV.2. Limit sets, attractors and Lyapunov functions 143

in view of Proposition IV.1, and hence the sublevel set V

is positively invariant.

Therefore, for every x 2 V

the set O

.x/ is compact and !.x/ ¤;and, in view of

Proposition IV.11, we have the convergence x t ! I.C/. Due to the coerciveness

of the function V there exists for every x 2 R

a real number a satisfying x 2 V

The proof is complete. 

Deﬁnition. A singular point x



of the vector ﬁeld X is called Lyapunov-stable or,

in short, L-stable (or C-stable), if every open neighborhood O of x



contains an

open neighborhood x



2 O

 O such that

 t  O for all t  0:

The point x



is called asymptotically stable, if the open neighborhood O

can, in

addition, be chosen such that O

 A.fx



g/ and hence

lim

t!1

x  t D x



for all x 2 O



Figure IV.8. Lyapunov stability (left) and asymptotic stability (right).

Theorem IV.13 (Lyapunov). Let x



be a singular point of the vector ﬁeld X and

let U be an open neighborhood of x



and let V W U ! R be a continuous function

that is differentiable on U nfx



g.If

(1) V.x



/ D 0 and V.x/>0for x 2 U nfx



(2)

V.x/ 0 for x 2 U nfx



then, x



is L-stable.

If, in addition, the inequality in (2) is strict, then x



is asymptotically stable.

Proof. If O is an open neighborhood of x



, we choose a closed ball B



/ 

U \ O, where ı>0. Since the function V is continuous and since the boundary



/ is compact, it follows from (1) that

˛ ´ inffV.x/ j x 2 @B



/g >0:

We deﬁne the open neighborhood O

´fx 2 B



/ j V.x/<˛g of x



and

choose a point x 2 O

. In view of (2) we have V.x  t/  V.x/<˛, and since

144 Chapter IV. Gradientlike ﬂows

V  ˛ on @B



/, the continuous curve x  t cannot leave the ball B



/ for

t  0. Therefore, the open set O

is positively invariant under the ﬂow and the

point x



is L-stable.

We assume now that

V.x/<0for all x 2 U nfx



g and show for every



¤ x 2 O

that x  t

! x



for every sequence t

!1. Arguing by

contradiction we ﬁnd, due to the compactness of



/, a convergent sequence

x  t

! y



¤ x



;

where y



2 B



/. In view of the assumptions, V.y



/>0. Moreover, the

function V.z  t/ is strictly decreasing for every z 2 U nfx



g. It follows that

./V.x t/  V.y



/>0 for all t  0; and V.y



 s/<V.y



/ if s>0:

Since the function V is continuous, there exists an open neighborhood U

of y



within which

V.y  s/<V.y



/ if s  1 and y 2 U

However, for n large, the point x t

is in U

and therefore V.x.t

Cs//<V.y



in contradiction to ./. The proof of Theorem IV.13 is complete. 

Remark. In physics, one can often take the energy as a Lyapunov function V .In

this case the L-stable point x



is a local minimum of the energy.

Example. We study the pendulum with linear friction which is determined by the

ordinary differential equation of second order

Rx C sin x D Px

with a positive constant >0. The equation is equivalent to the system of equations







sin x  y



μ X.x; y/ 2 R

As usual, we work in the covering space R

of the phase space S

 R. Since

the vector ﬁeld X is linearly bounded, the ﬂow '

exists for all times, in view of

Proposition IV.3.

The energy function H W R

! R, deﬁned by

H.x;y/ ´

 cos x 1;

is a Lyapunov function, since

H.x;y/ DhrH.x;y/;X.x;y/iDy

 0:

In particular,

H.x;y/ D 0 if and only if y D 0. Therefore, the function

H.'

.x; y// is strictly decreasing outside of the set fy D 0g. Since the gradient

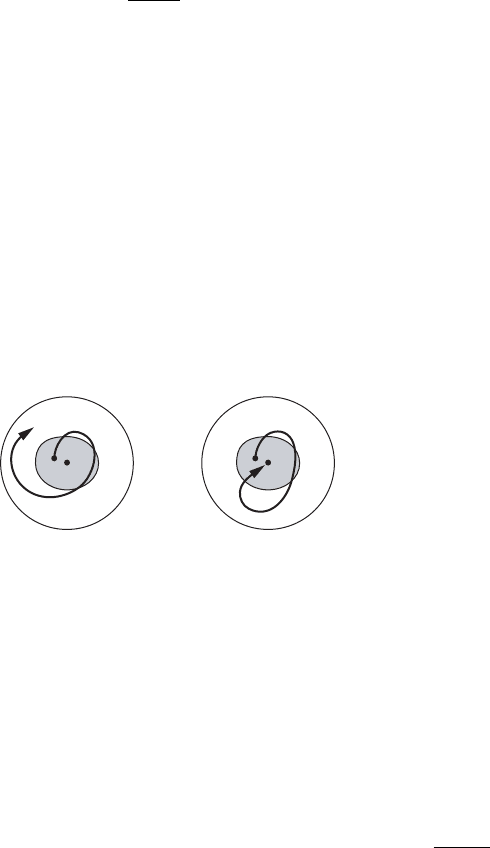
IV.2. Limit sets, attractors and Lyapunov functions 145

H D 1

H<1 H>1



Figure IV.9. Level sets of the energy H and a few solutions.

rH is orthogonal to the levellines of the function H , the vectorﬁeld X is transversal

to the level lines in all the points .x; y/ satisfying y ¤ 0.

We consider the set

C ´f.x; y/ 2 R

H.x;y/ D 0gDfy D 0g:

In order to determine the maximal invariant set I.C/ in C we assume that the

solution .x.t/; y.t// 2 C remains in C for all t 2 R. Then sin x.t/  0 and

consequently the function x.t/ D k is constant, where k 2 Z.

Conversely, these points lie in I.C/, since they are equilibrium points, so that

the maximal invariant set in C , given by

I.C/ Df.k; 0/ j k 2 Zg;

is the set of the singular points of the vector ﬁeld X.

If the solution z.t/ D .x.t /; y.t// 2 R

is bounded for t  0, then the closure

.z.0// of the orbit is compact and by Proposition IV.11,

z.t/ ! I.C/ as t !1:

Because the set I.C/ is discrete, there exists a unique integer k 2 Z such that

z.t/ ! .k; 0/; t !1;

and the pendulum converges to the highest or to the lowest position. We shall prove

that, since >0, every solution is bounded in R

for t  0.

Proof. (1) We ﬁrst verify that the function y.t/ is bounded for t  0. Since the

146 Chapter IV. Gradientlike ﬂows

function H.'

.z// is decreasing along every solution,

y.t/

D H.z.t// C cos x.t/

 H.z.0// C 1

μ M.z.0//;

where we have deﬁned the positive constant M D M.z.0// > 0. In terms of

physics, the kinetic energy is bounded by the initial energy.

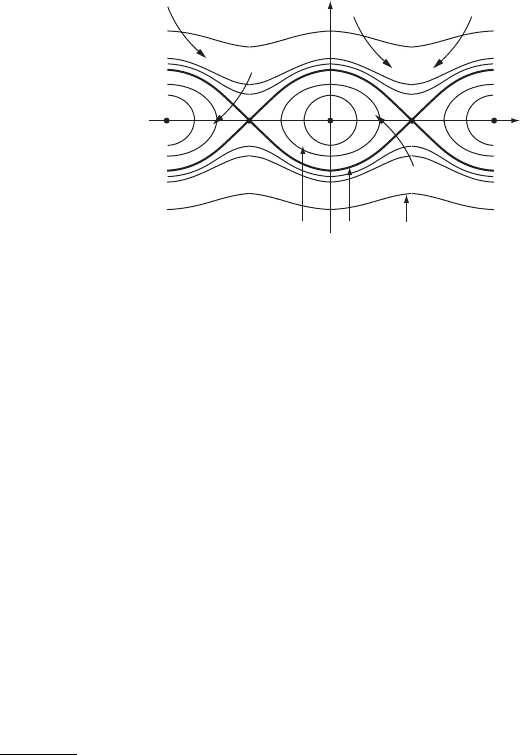
(2) We next show that the function x.t/ is bounded for t  0.

Every eye A

in Figure IV.10 is a bounded set which is positively invariant,

since the function H is decreasing along the solutions and is, on the boundary @A

equal to H D 1.

fH  1g

Figure IV.10. An eye A

Everysolution z.t/, which is not constant and which hits the separatrix fH D 1g,

remains in one of the eyes A

for all future times, since the function H.z.t// is

strictly decreasing outside of the set fy D 0g.

We assume that there exists a solution z.t/ D .x.t/; y.t// whose function x.t/

is not bounded. Then, in view of the above discussion, '

.z.0// …fH  1g for all

t  0, and so,

.z.0// 2fH>1g;t 0:

P D 2k

P C 

P  

x.t



Figure IV.11. To prove that x.t/ is bounded.

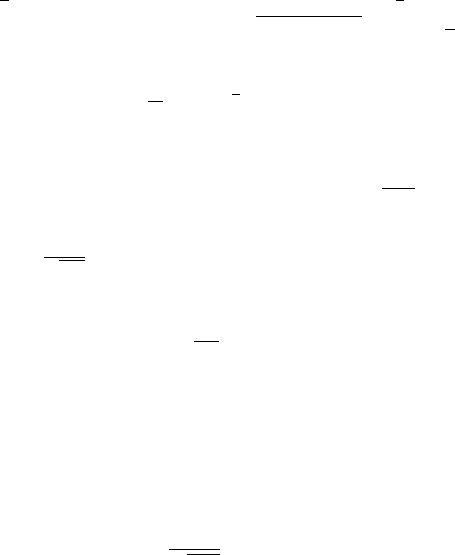
IV.2. Limit sets, attractors and Lyapunov functions 147

In particular, sign y.t/ is constant (no oscillation of the pendulum), so that z.t/

lies completely above or below the branches of the separatrix. We assume that

sign y.t/ DC1. Because x.t/ is continuous and not bounded, there exists, in view

of the mean value theorem, for every integer k 2 Z sufﬁciently large, a time t

2 R

at which x.t

/ D 2k 

 and a time t

2 R at which x.t

/ D 2k C

.

The branches of the separatrix are given by jyjD

2.cos x C 1/ Dj2 cos

so that the function y.t/ satisﬁes

jy.t/jj2 cos.k 



/jD2



μ d

on the interval t

 t  t

. From

 D x.t

/  x.t

/ D

Px./ d D

y./d  .t

 t

we conclude that t

 t





with the previously deﬁned constant M D

M.z.0// > 0. Consequently,

H.'

.z//  H.'

.z// D

d

H.'



.z// d 

H.'



.z// d 

D

y. /

d

.t

 t

/d





d

μ K: 

Hence, the function H.'

.z.0/// decreases on the interval Œt

 at least by the

ﬁxed amount K ¤ 0. Since this is true for every k sufﬁciently large, it follows that

H.'

.z.0/// !1;t!1:

This, however, is impossible, because H 1 on all of R

. The case sign y.t/ D

1 is completely analogous and we see that every solution z.t/is bounded for t  0

and consequently approaches an equilibrium point in the future.

There are three types of solutions of the pendulum with friction. Either, a

solution

(1) is constant and sits in one of the equilibrium points, or

(2) rotates at most ﬁnitely many times, then slows down and converges, possibly

with oscillations, to the lowest position of the pendulum, or

148 Chapter IV. Gradientlike ﬂows

(3) rotates at the most ﬁnitely many times, slows down and converges without

oscillations to the highest position of the pendulum.

In any case, due to the friction, every movement of the pendulum eventually comes

to a standstill. Clearly, most of the solutions (in the sense of Baire category and in

the sense of Lebesque measure) are of type (2).

Remark. We consider the linearized vector ﬁeld

DX.k; 0/ D



cos k 



at the singular points. In the point P D .2k; 0/ the matrix has the eigenvalues



1;2

. ˙ i

4  

which both have a negative real part. These points are attractive equilibrium points.

In the points P D ..2k C 1/; 0/, the eigenvalues



1;2

. ˙



C 4/

are real and satisfy Re 

<0<Re 

Hence, the points P D ..2k C 1/; 0/ are hyperbolic ﬁxed points of the ﬂow

maps '

for T>0. The initial conditions of the solutions of type (3) constitute

the stable manifold W

.P / of the hyperbolic ﬁxed point P . Itisaone-dimensional

submanifold of R

. The stable manifold converges without rotations, as illustrated

in Figure IV.12, to an attracting equilibrium point.

.1/

.2/

.3/

Figure IV.12. Every solution of the pendulum with friction approaches an equilibrium point

in the future.

Literature. For the qualitative theory of ordinary differential equations we recom-

mend the book [5] by H. Amann.

IV.3. Gradient systems 149

IV.3 Gradient systems

Let us recall ﬁrst the deﬁnition of the gradient vector ﬁeld rV W R

! R

of a

function

V W R

! R

of class C

rC1

, where r  1, with respect to the Euclidean scalar product h; i.At

every point x 2 R

, the derivative of the function V can be represented by means

of the Euclidean scalar product with the unique vector rV.x/ satisfying

hrV.x/;uiDdV .x/u for all u 2 R

The vector ﬁeld rV W R

! R

obtained this way belongs to the class C

. The

function V is a Lyapunov function for the ﬂow '

of the (negative) gradient vector

ﬁeld

Px DrV.x/; x 2 R

Indeed, using the chain rule and the deﬁnition of the ﬂow one computes

V.'

.x// D dV.'

.x//

.x/

D dV.'

.x//.rV.'

.x///

D hrV.'

.x//; rV.'

.x//i

D jrV.'

.x//j

so that the derivative of the function V along the ﬂow is given by

V.x/D jrV.x/j

 0; x 2 R

In this special case, the Lyapunov-function V decreases strictly along the non-

constant solutions. The !- (and !



-) limit sets of the orbits consist of critical

points of V and hence in view of Theorem IV.10 are contained in the set

C Dfx 2 R

V.x/D 0gDfx 2 R

jrV.x/ D 0g:

By Proposition IV.8 the limit sets are connected. Hence, if the critical points are

isolated, there exists for every solution x  t which is bounded in t  0 a unique

critical point x



of V such that

x  t ! x



;t!C1:

Similarly, there exists for every solution x  t which is bounded in t  0 a critical

point y



satisfying x  t ! y



as t !1.

In short, bounded solutions come from critical points of the function V and also

go to critical points. From Proposition IV.12 we deduce the following result.

150 Chapter IV. Gradientlike ﬂows

Theorem IV.14. If the function V W R

! R of class C

is coercive, i.e., V.x/ !1

as jxj!1, then every solution of the gradient equation Px DrV.x/is bounded

in t  0, for every x 2 R

and t

.x/ D1. Moreover,

x  t !fy 2 R

jrV.y/ D 0g; as t !1:

If the critical points of the function V are isolated, there exists for every x 2 R

critical point x



of V such that x  t ! x



as t !1.

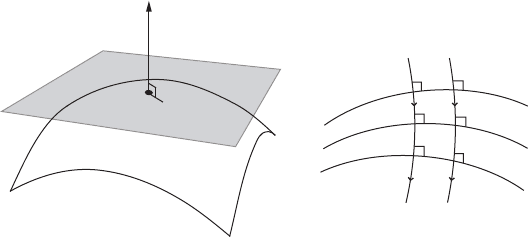
The gradient rV is orthogonal to the regular level surfaces

Dfx j V.x/ D cg

of the function V , so that the solutions of Px DrV.x/are orthogonal to the level

surfaces of V . Indeed, in every point x 2 N

of a regular level surface, the tangent

space is given by

Df 2 R

j dV .x/ D 0gDf 2 R

jhrV.x/;iD0g:

Clearly, gradient systems do not admit non-constant periodic solutions, because

V decreases strictly along non-constant solutions.

rV.x/

Figure IV.13. The tangent space T

is orthogonal to rV.x/(left). Orthogonal trajectories

to the level surfaces with c

(right).

Example. In R

we consider the coercive function

V.x;y/ D x

.x  1/

C y

and the corresponding gradient equation

Px DrV.x;y/ D.2x.x  1/.2x  1/; 2y/: