Zehnder E. Lectures on Dynamical Systems: Hamiltonian Vector Fields and Symplectic Capacities
Подождите немного. Документ загружается.


IV.4. Gradient systems on manifolds and Morse theory 171
for all x 2 M and all t 2 R.
(1) Diffeomorphism. We shall show that the flow map
ba
W M
b
! M
a
defines a diffeomorphism. To do this, it suffices to show that
ba
.M
b
/ D M
a
.
If
t
.x/ 2 M
b
a
, then
d
dt
V.
t
.x// D dV.
t
.x// X.
t
.x//
DhrV.
t
.x//; X.
t
.x//i
D˛.
t
.x// jrV.
t
.x//j
2
D1:
Therefore, as long as x and
t
.x/ 2 M
b
a
,wehave
V.
t
.x// V.
0
.x// D
Z
t
0
d
dt
V.
t
.x// dt Dt
or
./V.
t
.x// D V.x/ t:
If t D ba and V.x/ D b, we obtain V.
ba
.x// D a, so that
ba
.M
b
/ M
a
.
If V.x/ D a, then V.
.ba/
.x// D V.x/Cba D b, and the surjectivity follows.
(2) Construction of a retraction r
1
W M
b
! M
a
. We define for 0 t 1 and
x 2 M
b
the mapping r by
r.t;x/ D r
t
.x/ D
´
x; V.x/ a;
tŒV.x/a
.x/; a V.x/ b:
Then the map r W Œ0; 1 M
b
! M
b
is continuous and satisfies
r.0; x/ D x; x 2 M
b
;
r.t;x/ D x; x 2 M
a
and all t 2 Œ0; 1:
Using the identity ./ it follows that
V
tŒV.x/a
.x/
D .1 t/V.x/ C ta;
and setting t D 1 one concludes that r
1
.x/ D r.1; x/ 2 M
a
for all x 2 M
b
.
Therefore, M
a
is a strong deformation retract of M
b
, as claimed.
In sharp contrast to the above situation, the topological type of M
a
changes if
we pass a critical level.
Proposition IV.26. Let p 2 K \ V
1
.c/ be a nondegenerate critical point of the
C
2
function V W M ! R having the Morse index D .p/.Ifa<c<band if
M
b
a
\ K Dfpg;
172 Chapter IV. Gradientlike flows
then
H
j
.M
b
;M
a
/ D
´
R;jD .p/;
0; otherwise.
In particular, dim H
j
.M
b
;M
a
/ D 1 for j D .p/ and 0 otherwise.
Figuratively speaking, the sublevel set M
b
is homeomorphic to M
a
with a
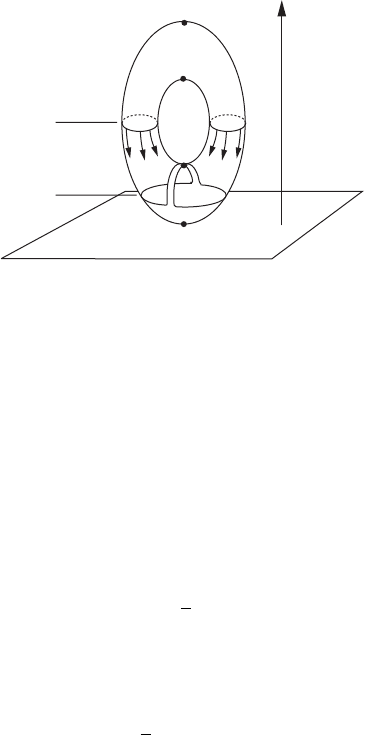
.p/-handle glued on, as illustrated in Figure IV.20 for the height function V on
the torus T
2
.
p
V
1
.a/
V
R
2
V
1
.b/
Figure IV.20. Passing the critical level of the saddle point p. The sublevel set M
a
with a
1-handle glued on is a deformation retract of M
b
.
For the proof of the proposition we first introduce convenient coordinates near
the critical point.
Lemma IV.27 (Morse lemma). We assume M to be a smooth manifold of dimension
d and m 2 M to be a nondegenerate critical point of the smooth function F W M !
R, such that dF .m/ D 0. Moreover, we assume the Hesse matrix d
2
F .m/ to be
nondegenerate. Then there exist local smooth coordinates W U R
n
! M near
m satisfying .0/ D m, in which the function f.x/ D F B .x/ is written as
f.x/ D f .0/ C
1
2
d
2
f .0/.x; x/:
Proof [Deformation trick by R. Thom and J. Moser]. Choosing local coordinates
we may assume that the function f W R
d
! R has the form
f.x/ D f .0/ C
1
2
d
2
f .0/.x; x/ C O
3
.x/;
by using the Taylor formula. Moreover, we may assume that f .0/ D 0. With the
Hesse matrix H we obtain d
2
f .0/.x; x/ DhHx;xi, so that the function has the
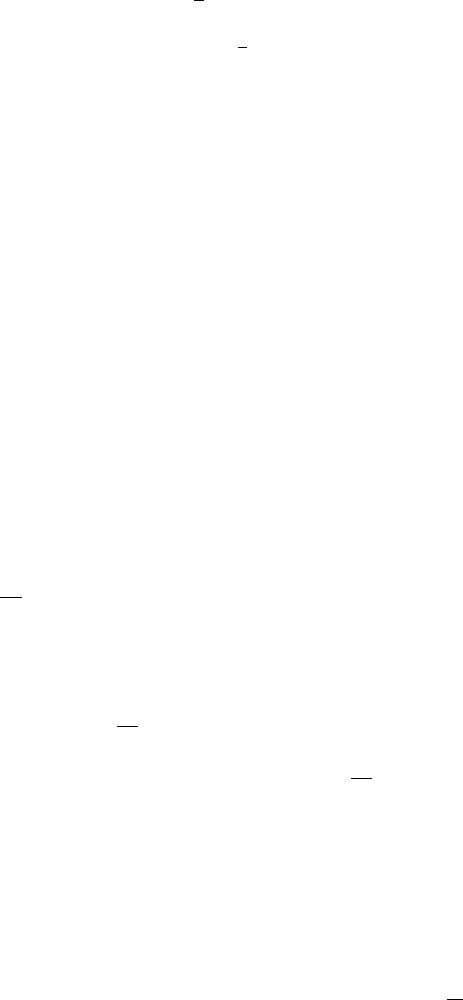
IV.4. Gradient systems on manifolds and Morse theory 173
form
f.x/ D
1
2
hHx;xiCO
3
.x/:
We introduce the function g by g.x/ D
1
2
hHx;xi and look for a local diffeomor-
phism near x D 0, satisfying .0/ D 0 and
.
f /.x/ D g.x/
for all x near 0. For this, it suffices to find a local diffeomorphism leaving the
origin fixed and satisfying
df D dg
near x D 0. We now deform these two 1-forms into each other and define the
family !
t
of 1-forms by
!
t
D tdf C .1 t/dg; 0 t 1:
Then !
1
D df and !
0
D dg, moreover, d!
t
D 0. More ambitiously, we look for
a family
t
of local diffeomorphisms satisfying
0
D Id and
t
.0/ D 0 such that
./.
t
/
!
t
D dg; 0 t 1
for all x near 0. The desired result then follows for the parameter value t D 1.
We now assume that the family
t
of local diffeomorphisms is the flow of a
time dependent vector field X
t
which is defined near x D 0 and which has the
property that X
t
.0/ D 0 for all 0 t 1. The flow satisfies
d
dt
t
.x/ D X
t
.
t
.x//; 0 t 1; and
0
.x/ D x:
In order to find the vector field X
t
, we differentiate the equation ./ in the
variable t and find, using the formula of Proposition V.14,
0 D
d
dt
.
t
/
!
t
D .
t
/
di
X
t
!
t
C i
X
t
d!
t
C
d
dt
!
t
D .
t
/
dŒi
X
t
!
t
C f g:
We therefore look for a vector field X
t
which solves the linear equation
./i
X
t
!
t
D g f; X
t
.0/ D 0
near x D 0 for all 0 t 1. If we have found such a vector field, then the lemma is
proved, because we can make all our steps backwards. Namely, the flow
t
exists
for all 0 t 1 and for all x near 0 and satisfies
t
.0/ D 0 and
d
dt
.
t
/
!
t
D 0.

174 Chapter IV. Gradientlike flows
Consequently, .
t
/
!
t
D .
0
/
!
0
D dg for all 0 t 1 and for t D 1 we
obtain the desired solution
1
D .
The equation ./ for X
t
has a smooth solution, since using the Taylor formula
and !
t
.x/Œh DhHx;hiCtO
2
.x/Œh, the equation ./ to be solved becomes
˝
X
t
.x/; ŒH C tR.x/h
˛
DhQ.x/; hi
for all x near 0, with a smooth matrix function R.x/ and with a smooth vector func-
tion Q.x/ satisfying R.0/ D 0 and Q.0/ D 0. The Hesse-matrix H is symmetric
and invertible, in view of the assumption of nondegeneracy. Therefore, the desired
vector field X
t
is given by
X
t
.x/ D
H C tR.x/
T
1
Q.x/
and satisfies the equation ./ for all x near 0, and, moreover, satisfies X
t
.0/ D 0
for all 0 t 1. This proves the lemma.
Proof of Proposition IV.26 [Sketch]. We abbreviate by D .p/ the Morse index
of the critical point p and choose by means of the Morse lemma local coordinates
near p in which p D 0, and in which the function V has the normal form V.z/ D
V .0/ C
1
2
d
2
V .0/.z; z/, with the Hesse-matrix
H D d
2
V .0/ D
1
0
0 1
d
in 0. Then, we have the coordinates z D .x; y/ 2 D
D
d
with the two small
discs D
Dfx 2 R
jjxj"g and D
d
Dfy 2 R
d
jjyj"g. Assuming
V .0/ D 0 the function V is of the form
V.x;y/ Djyj
2
jxj
2
;.x;y/2 D
D
d
:
Locally near 0 the sublevel sets are depicted in Figure IV.21.
Introducing the subset H of the type of a handle connecting the two pieces of
the sublevel set V
a
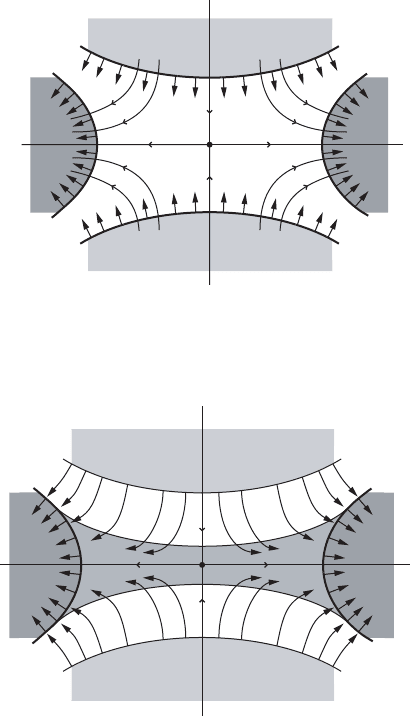
as shown in Figure IV.22 one can see by slowing down the
gradient flow that the set V
a
[ H is a deformation retract of V
b
.
Therefore, borrowing from topology again, we deduce the isomorphism in co-
homology
H
.V
b
;V
a
/ Š H
.V
a
[ H; V
a
/:
With the two disjoint pieces H
1
H attached to V
a
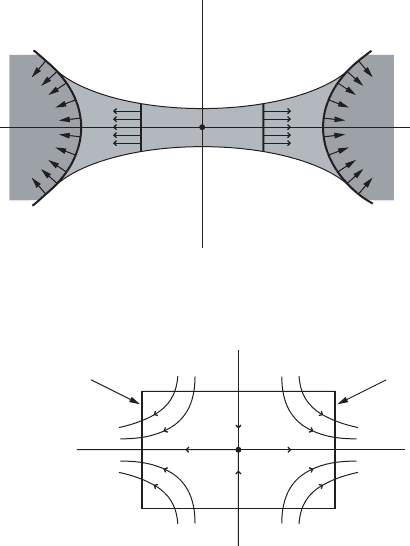
as indicated in Figure IV.23
we see that V
a
V
a
[ H
1
V
a
[ H and conclude that the sublevel set V
a
is a
deformation retract of the set V
a
[ H
1
.
Consequently, we arrive at the isomorphism
H
.V
a
[ H; V
a
/ Š H
.V
a
[ H; V
a
[ H
1
/:
IV.4. Gradient systems on manifolds and Morse theory 175
x
y
p
V
1
.a/
V
1
.a/
V
1
.b/
V
1
.b/
V
a
V
a
V
b
V
b
Figure IV.21. Level sets and gradient flow locally near the critical point p.
x
y
V
a
V
a
H
Figure IV.22. The deformation retract V
a
[ H of V
b
.
Now cutting off the interior of the parts both spaces of the pair .V
a
[H; V
a
[H
1
/
have in common, we obtain a pair of spaces that is homotopically equivalent to the
pair illustrated in Figure IV.24.
Using now the cohomology results about excisions and homotopy equivalences
one obtains the isomorphism
H
V
a
[ H; V
a
[ H
1
Š H
D
D
d
;@D
D
d
;
176 Chapter IV. Gradientlike flows
x
y
V
a
V
a
H
1
H
1
Figure IV.23. Deformation of V
a
[ H
1
to V
a
.
x
y
@D
D
d
@D
D
d
Figure IV.24. After excision.
where the two discs are defined by
D
Dfx jjxjrgR
;
D
d
Dfy jjyjrgR
d
for a small radius r.
The pair of spaces on the right-hand side of the above isomorphism is of the
same homotopy type as the pair .D
;@D
/, because the disc D
d
is contractible.
Consequently,
H
D
D
d
;@D
D
d
Š H
.D
;@D
/:
Summing up, we have so far sketched the proof of the isomorphism
H
.V
b
;V
a
/ Š H
.D
;@D
/:
IV.4. Gradient systems on manifolds and Morse theory 177
Now,
H
j
.D
;@D
/ D
´
R; if j D ,
0; otherwise.
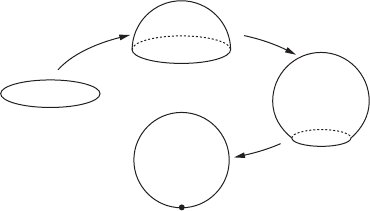
This can be easily verified by collapsing the boundary @D
into a point (proceed-
ing as in Figure IV.25). From this we obtain the isomorphism H
.D
;@D
/ D
H
.S
; /. Using this, we finally arrive at the desired result,
D
@D
@
@
S
Figure IV.25. Collapsing @D
into a point.
H
j
.V
b
;V
a
/ D
´
R; if j D ,
0; otherwise.
This finishes the sketch of the proof of Proposition IV.26. All the details of this
sketch, including the necessary tools from algebraic topology, can be found in the
book [55] by J. Jost.
In Proposition IV.26 we have considered only one critical point and thus have
obtained only one handle. If several critical points are lying on the same level, we
obtain, with the same local arguments applied in disjoint sets, several handles and
therefore arrive at the following proposition.
Proposition IV.28. We assume that fp
1
;p
2
;:::;p
m
g2K \ V
1
.c/ are non-
degenerate critical points having the Morse indices .p
j
/.Ifa<c<band
if
K \ M
b
a
Dfp
1
;p
2
;:::;p
m
g;
then
H
j
.V
b
;V
a
/ D R ˚˚R D R
s
j
;
where the integer s
j
is the number of critical points p in fp
1
;p
2
;:::;p
m
g whose
Morse index is equal to .p/ D j .
178 Chapter IV. Gradientlike flows
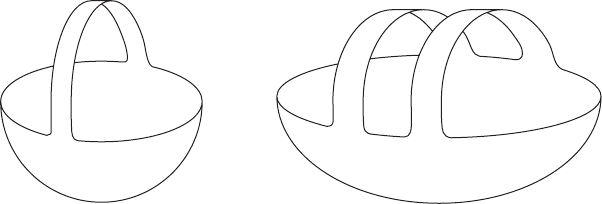
Figure IV.26. One handle (left) corresponds to one critical point, and two handles (right)
corresponding to two critical points.
The rest of the proof of the Morse equation is of more algebraic nature. We
begin with an easy lemma.
Lemma IV.29. Given a sequence
0 D A
0
a
0
! A
1
a
1
! A
2
a
2
! A
3
a
3
! A
4
a
4
!
a
k
! A
k
of linear maps a
j
between the vector spaces A
j
. If the sequence is exact, so that
ker a
j C1
D Im a
j
for all j , then
dim A
1
dim A
2
CC.1/
k1
dim A
k
C .1/
k
dim .Im a
k
/ D 0:
Proof. From the exactness assumption we obtain the equations
dim A
j
D dim .ker a
j
/ C dim .Im a
j
/
D dim .Im a
j 1
/ C dim .Im a
j
/
and Im a
0
D 0. The lemma now follows by induction.
We borrow again from algebraic topology. If X Y Z is a triple of
manifolds, then there exists the so-called long exact sequence
0 ! H
0
.X; Y / ! H
0
.X; Z/ ! H
0
.Y; Z/
ı
0
! H
1
.X; Y / ! H
1
.X; Z/ ! H
1
.Y; Z/
ı
1
! H
2
.X; Y / ! H
2
.X; Z/ ! H
2
.Y; Z/
ı
2
!:
Introducing the non-negative integers
r
j
.X; Y / ´ dim H
j
.X; Y /;
j
.X;Y;Z/ ´ dim .Im ı
j
/;
IV.4. Gradient systems on manifolds and Morse theory 179
it follows from Lemma IV.29 that for every m,
m
X
j D0
.1/
j
Œr
j
.X; Y / r
j
.X; Z/ C r
j
.Y; Z/ .1/
m
m
.X;Y;Z/ D 0;
and so, by subtraction,
./.1/
m1
m1
.X;Y;Z/ D .1/
m
m
.X;Y;Z/ .1/
m
r
m
.X; Y /
C .1/
m
r
m
.X; Z/ .1/
m
r
m
.Y; Z/:
We define the following polynomials in the variable t,
P.t;X;Y/ ´
X
m0
r
m
.X; Y / t
m
;
Q.t;X;Y;Z/ ´
X
m0
m
.X;Y;Z/ t
m
:
Multiplying the equation ./ by .1/
m
t
m
and adding up the equations we obtain
the following equation.
Lemma IV.30. If X Y Z is a triple of manifolds, then
.1 C t/Q.t; X; Y; Z/ D P.t;X;Y/ P.t;X;Z/C P.t;Y;Z/:
We are finally ready to complete the proof of Theorem IV.20.
Proof of Theorem IV.20. If c
1
<c
2
<c
3
< <c
N
are the critical values of
the function V W M ! R, then c
1
D min
x2M
V.x/ and c
N
D max
x2M
V.x/.We
choose real numbers d
0
< <d
N
, satisfying
d
0
<c
1
<d
1
<c
2
<d
2
< <c
N
<d
N
:
Since c
1
is the minimum we have M
d
0
D;and since c
N
is the maximum,
M
d
N
D M , and we obtain the following filtration of M :
;DM
d
0
M
d
1
M
d
N
D M:
Applying Lemma IV.30 to the triple M
d
0
D;M
d
j 1
M
d
j
leads to the
equation
P.t;M
d
j
;M
d
j 1
/ D P.t;M
d
j
; ;/P.t;M
d
j 1
/C.1Ct /Q.t; M
d
j
;M
d
j 1
; ;/:
Adding up these equations we arrive at the identity
N
X
j D1
P.t;M
d
j
;M
d
j 1
/ D P.t;M;;/ C .1 C t/Q.t/
D P.t;M/C .1 C t /Q.t/;
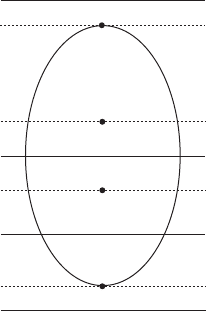
180 Chapter IV. Gradientlike flows
d
0
d
1
d
2
d
N
c
1
c
2
c
3
c
N
Figure IV.27. Schematically, the levels in the proof of Theorem IV.20.
in which P.t;M/ is the Poincaré polynomial of the manifold M . In view of
Proposition IV.28 we obtain for the left-hand side the polynomial
N
X
j D1
P.t;M
d
j
;M
d
j 1
/ D
dim M
X
kD0
t
k
m
k
D m.t; V /;
which is the Morse polynomial. This completes the sketch of Theorem IV.20.As
already pointed out, the details can be found in the book [55] by J. Jost.
We would like to mention the far-reaching generalization of the above Morse
theory to continuous flows on locally compact metric spaces, due to C. Conley.
Generalizing the Morse index of a nondegenerate equilibrium point of the gradient
flow, C. Conley associates with an isolated invariant set of a continuous flow the
so-called Conley index, which is the homotopy type of a pointed topological space.
In the case of the nondegenerate equilibrium point above, the Conley index is the
pointed sphere having the dimension of the Morse index. Conley’s index theory is
one of the most powerful tools relating dynamics to invariants of algebraic topology.
With a Morse decomposition of a compact invariant set of a continuous flow one can
also associate a Morse equation generalizing Theorem IV.20. The main advantage of
Conley’s theory in the applications are the invariance properties under deformations.
Literature. In the above presentation of Morse theory we followed the correspond-
ing sections in the book [55] by J. Jost, in which one also finds an introduction into
the required algebraic topology. The book on Morse theory by J. Milnor [68]isa
classic. Presentations of the theory can also be found in the books [21] by L. Con-
lon, [101] by J. Schwartz, [79] by R. S. Palais and Chun-lian Terng and [9]by
