Zehnder E. Lectures on Dynamical Systems: Hamiltonian Vector Fields and Symplectic Capacities
Подождите немного. Документ загружается.

IV.4. Gradient systems on manifolds and Morse theory 161
In view of cat.T
2
/ D 3, every function on the 2-torus must have at least three
critical points according to the Lusternik–Schnirelman theorem. The above exam-
ple represents therefore a minimal model having precisely three critical points. One
of the critical points (in our example the monkey saddle) is necessarily degener-
ate. Indeed, we shall see in the next section that the Morse theory guarantees at
least four critical points for functions on the 2-torus whose critical points are all
nondegenerate.
Literature. For a view of the state of the art in Lusternik–Schnirelman category
we point out the monograph [22] by O. Cornea, G. Lupton, J. Oprea and D. Taure.
The Lusternik–Schnirelman category is treated in books about nonlinear functional
analysis, as for example in [26] by K. Deimling and in [101] by J. Schwartz.
The Lusternik–Schnirelman theory on Banach manifolds is developed in [77]by
R. S. Palais.
IV.4 Gradient systems on manifolds and Morse theory
We finally describe the relation between the dynamics of gradient flows and the
topology of the underlying manifold. We assume M to be a (smooth) compact
manifold of dimension dim M D d (as for example a d -dimensional compact
submanifold of the R
N
). We choose a Riemann metric g on M , so that there exists
at every point x 2 M a scalar product g.x/ (symmetric and positively definite) in
the tangent space,
g.x/.; / μh; i;;2 T
x
M:
The induced norm on the tangent space in x is defined by
g.x/.; / Dh; iμjj
2
;2 T
x
M:
The scalar product depends differentiably on the base point x.
If V W M ! R is a function of class C
2
, its derivative dV .x/ at the point x 2 M ,
dV .x/W T
x
M ! R;
is a linear function. Hence there exists a unique vector rV.x/ 2 T
x
M satisfying
g.x/.rV.x/;/ D dV .x/ for all vectors 2 T
x
M;
or in short,
hrV.x/;iDdV .x/; 2 T
x
M:
The vector rV.x/ is called the gradient vector of the function V in x.Itdepends
on the choice of the metric. The vector field rV on M obtained this way is
differentiable. The flow of the equation
Px DrV.x/; x 2 M
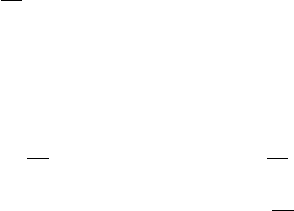
162 Chapter IV. Gradientlike flows
is called the gradient flow of the function V on M . It is defined by
d
dt
'
t
.x/ DrV.'
t
.x//; '
0
.x/ D x; t 2 R;
and is, in view of Proposition IV.1, a complete flow.
Again, the function V is decreasing along the parametrized orbits of the flow,
as the by now familiar computation shows,
d
dt
V.'
t
.x// D dV.'
t
.x//
d
dt
'
t
.x/
DhrV.'
t
.x//;
d
dt
'
t
.x/i
D hrV.'
t
.x//; rV.'
t
.x//i
D jrV.'
t
.x//j
2
0:
The function V decreases strictly along non-constant orbits and all the results about
gradientlike flows are applicable.
Definition. A point x 2 M is called a critical point of the function V W M ! R,
if dV .x/ D 0, or equivalently, if rV.x/ D 0 in T
x
M . The set of critical points is
again denoted by K,
K Dfx 2 M jrV.x/ D 0g:
We briefly recall the results about gradientlike flows on compact spaces. In
view of Theorem IV.19 the number of critical points is estimated from below by
#K cat
M
.M /. Since the solutions are bounded, we have for every point x 2 M
the convergence
x t ! K; t !˙1:
In other words, every solution approaches the critical set K in forward and in
backward time. If the critical points are isolated, there exist only finitely many of
them, since M is compact, so that
K Dfx
1
;x
2
;:::;x
N
g:
With every point x … K in the manifold M we can associate a pair k ¤ j of indices
such that
x t ! x
k
;t!C1;
x t ! x
j
;t!1:
In the following, we make additional assumptions on the critical points K.
IV.4. Gradient systems on manifolds and Morse theory 163
Definition. A critical point x
k
2 K is called nondegenerate, if, in local coordinates
around x
k
, the bilinear form
d
2
V.x
k
/.u; v/ 2 R;u;v2 R
d
;
defined by the Hesse matrix of V in x
k
, is nondegenerate. In view of rV.x
k
/ D 0
this definition is independent of the choice of the local coordinates.
For the linearized gradient vector field at the critical point x
k
, we then have (in
local coordinates)
hd rV.x
k
/u; viDd
2
V.x
k
/.u; v/; u; v 2 R
d
:
The local invariants in x
k
are the dimensions of the subspaces of R
d
, on which
the bilinear form is positive respectively negative. Hence the tangent space splits,
T
x
k
M D E
C
x
k
˚ E
x
k
so that, for u D u
C
C u
2 E
C
x
k
˚ E
x
k
,
d
2
V.x
k
/.u
C
;u
C
/>0; u
C
¤ 0;
d
2
V.x
k
/.u
;u
/<0; u
¤ 0:
Again, this is independent of the choice of the coordinates and the metric.
Definition. The Morse index of the function V at the critical point x
k
is the integer
.x
k
/ ´ dim E
x
k
:
Obviously, 0 .x
k
/ d . The linearization of the gradient vector field at the
critical point x
k
is symmetric with respect to the scalar product and has therefore d
real eigenvalues. The number of negative eigenvalues is equal to .x
k
/, the number
of positive eigenvalues is equal to d .x
k
/. Therefore, the equilibrium point x
k
of
rV.x/on M is a hyperbolic equilibrium point according to Lemma II.12, and its
unstable manifold W
.x
k
/ Dfx 2 M j x t ! x
k
; as t ! 1g is of dimension
.x
k
/ D dim W
.x
k
/:
Here, the concept of hyperbolicity has been somewhat generalized by admitting
the cases .x
k
/ D 0 and .x
k
/ D d, in which T
x
k
M D E
x
k
˚ E
C
x
k
Df0g˚
E
C
x
k
respectively T
x
k
M D E
x
k
˚f0g. We set W
˙
.x
k
/ Dfx
k
g, in the cases
dim E
˙
.x
k
/ D 0.
Definition. A function V W M ! R of class C
2
is called a Morse function, if all its
critical points are nondegenerate.
In a sufficiently small neighborhood of a nondegenerate critical point, there
do not exist other critical points. This follows from the inverse function theorem.
164 Chapter IV. Gradientlike flows
In particular, a Morse function on a compact manifold admits only finitely many
critical points.
We should mention that on every compact manifold (without boundary) there
exists an abundance of Morse functions. Every smooth function can be uniformly
approximated together with all its derivatives by Morse functions, as is demon-
strated, for example in the book [21] by L. Conlon.
As already pointed out, x t ! K as t !1for every point x 2 M . In the
case of nondegenerate critical points we conclude that the compact manifold M is
composed of the unstable manifolds of the critical points,
M D
[
x
k
2K
W
.x
k
/:
Examples. (1) We consider the sphere S
2
R
3
standing on R
2
and the height
function V W S
2
! R measuring the levels over R
2
, as shown in Figure IV.16.
Then, V has two critical points, namely, the maximum at the north pole N satisfying
.N / D 2 and the minimum in S having the Morse index .S/ D 0.
R
2
S
N
V
Figure IV.16. The height function on S
2
having the two critical points N and S , the maximum
and the minimum. Also indicated are some flow lines.
(2) If T
2
R
3
is the embedded torus as depicted in Figure IV.17 and if the
function V W T
2
! R is again the height function, then there exist one maximum
having Morse index 2 and one minimum having index 0 as before. However, there
exist two additional critical points S
1
;S
2
which are saddle points whose Morse
indices are equal to .S
i
/ D 1.
Since all the points x 2 M move under the gradient towards critical points,
one expects a relation between the local invariants .x
k
/ of the flow at the critical
points x
k
2 K, and the topological invariants of the manifold M .

IV.4. Gradient systems on manifolds and Morse theory 165
R
2
V
S
1
S
2
Figure IV.17. The height function on T
2
having four critical points and some flow lines of
its gradient flow.
The dynamical data of a Morse function V are collected in the Morse polynomial
of V , defined by
m.t; V / ´
X
fx jrV.x/D0g
t
.x/
;
where .x/ is the Morse index of the critical point x.Bym
j
, we denote the number
of critical points whose Morse index is equal
m
j
D #fx 2 K j .x/ D j g:
Then the number of critical points is equal to #K D
P
dim M
j D0
m
j
and the Morse
polynomial becomes
m.t; V / D
dim M
X
j D0
m
j
t
j
:
In particular, # K D m.1; V /.
On the other hand, also the topological data of M are collected in a polynomial.
For this we need the Betti numbers ˇ
j
D ˇ
j
.M / of M . The j -th Betti number
is defined as the dimension of the vector space H
j
.M / of the j -th cohomology
group of M . In view of the theorem of de Rham this vector space is isomorphic to
the real vector space of the closed j -forms modulo the exact j -forms on M ,
H
j
.M / Š
f! 2
j
.M / j d! D 0g
f! 2
j
.M / j ! D d˛; ˛ 2
j 1
.M /g
;1 j dim M;
and, for j D 0,
H
0
.M / Šf! 2
0
.M / j d! D 0g:
166 Chapter IV. Gradientlike flows
Here
j
.M / denotes the space of the j -forms on M and d W
j
.M / !
j C1
.M /
is the exterior derivative acting on forms.These concepts will be introduced in the
next chapter. The exterior derivative satisfies d Bd D 0, so that every exact form is
a closed form. As usual, we make use of the convention that
0
.M / D C
1
.M; R/
denotes the space of smooth functions. On
0
the exterior derivative d coincides
with the usual derivative.
The direct sum of the forms H
j
.M /, denoted by
H
.M / D
M
j
H
j
.M /;
is an algebra (with respect to the exterior product ^) and is called de Rham coho-
mology algebra.
The Poincaré polynomial of the compact manifold M is the polynomial
P.t;M/ ´
dim M
X
j D0
ˇ
j
t
j
:
The Betti numbers ˇ
j
D ˇ
j
.M / contain relevant information about the topology
of M .
Example. We consider the space
0
.M / D C
1
.M; R/ of smooth functions. The
function f 2
0
is a closed form, if df .x/ D 0 for all x 2 M . Hence, these are
the locally constant functions on M .IfM is connected, then f D constant so that
H
0
.M / Dff D const.gŠR:
Therefore
ˇ
0
D dim H
0
.M / D 1;
if M is connected. More generally, the dimension dim H
0
.M / is the number of
connected components of M .
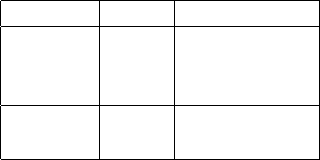
In the following table some Betti numbers ˇ
j
D ˇ
j
.M / are listed.
manifold genus Betti numbers
S
2
g D 0 .1; 0; 1/
T
2
g D 1 .1; 2; 1/
F
g
g .1; 2g; 1/
S
n
– .1;0;:::;0;1/
T
n
– ˇ
k
D
n
k
IV.4. Gradient systems on manifolds and Morse theory 167
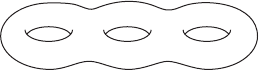
The manifold F
g
denotes a compact connected 2-dimensional manifold of
genus g, hence a closed surface having g holes, as illustrated in Figure IV.18.
Figure IV.18. A surface of genus g D 3.
The following theorem describes the relation between the gradient flow of a
Morse function and the topology of the manifold.
Theorem IV.20 (Morse inequalities). We assume that V W M ! R is a C
2
-function
on the compact manifold M whose critical points are all nondegenerate. Then
m.t; V / D P.t;M/C .1 C t/Q.t/;
where Q.t/ is a polynomial with non-negative integer coefficients. More explicitly,
dim M
X
j D0
m
j
t
j
D
dim M
X
j D0
ˇ
j
t
j
C .1 C t/Q.t/:
The sum on the left-hand side sums up the local invariants of the gradient flow
of the vector field rV on M defined by the Morse function V . The sum on the
right-hand side contains the topological invariants of the manifold M which are
independent of the choice of the function V and of the metric used.
We next draw some conclusions from the theorem.
Definition. The Euler characteristic of a compact manifold M is the integer
.M / ´
dim M
X
j D0
.1/
j
ˇ
j
D P.1; M /;
where ˇ
j
D ˇ
j
.M / are the Betti numbers of M .
Examples. From the above table for the Betti numbers we compute
.S
2
/ D 1 0 C 1 D 2;
.T
2
/ D 1 2 C 1 D 0;
.F
g
/ D 1 2g C 1 D 2 2g;
.S
n
/ D 1 C .1/
n
;
.T
n
/ D .1 1/
n
D 0:
168 Chapter IV. Gradientlike flows
Corollary IV.21. We assume M to be a compact manifold and V W M ! R a
function of class C
2
. If all the critical points are nondegenerate, then
dim M
X
j D0
.1/
j
m
j
D .M /;
where m
j
is the number of critical points x of the function V whose Morse index is
equal to .x/ D j .
Proof. We choose t D1 in Theorem IV.20.
The sum on the left-hand side of the equation in the corollary is independent
of the choice of the Morse function which at first sight is not evident. Conversely,
the topological Euler characteristic on the right-hand side is determined by the
dynamics of the gradient vector field rV on the manifold M .
Example. If the function V W F
g
R
3
! R, defined on the closed surface of
genus g, is of class C
2
and possesses only nondegenerate critical points, then
2 2g D m
0
m
1
C m
2
;
where m
0
is the number of local minima, m
1
the number of saddle points and m
3
the number of local maxima.
Special case.Ifm
0
D m
2
D 1 (there exists exactly one minimum and exactly
one maximum) then the number of saddle points is equal to m
1
D 2g.Ifg D 0,
that is, if the closed surface F
g
D S
2
is the sphere, then m
1
D 0, so that a Morse
function on the sphere S
2
having exactly one minimum and one maximum does
not admit any saddle points.
Corollary IV.22. If M is a compact manifold and if the function V W M ! R of
class C
2
has only nondegenerate critical points, then
m
j
ˇ
j
;0 j dim M:
In particular, the number of critical points K of the function V is estimated by
#K
dim M
X
j D0
ˇ
j
μ SB.M /:
Proof. The polynomial Q.t/ D
P
q
j
t
j
in Theorem IV.20 has only integer coeffi-
cients q
j
0. Therefore the estimates follow if we compare the coefficients of t
j
.
The second statement then follows recalling that #K D
P
dim M
j D0
m
j
.
IV.4. Gradient systems on manifolds and Morse theory 169
Examples.
SB.S
n
/ D 2;
SB.T
n
/ D .1 C 1/
n
D 2
n
:
In the case of the sphere there is, in comparison to the estimate involving the
Lusternik–Schnirelman category, no improvement. In the case of the torus we
obtain for the number of critical points #K the following stronger estimate
#K 2
n
D SB.T
n
/;
which improves the earlier estimate #K n C1 D cat
T
n
.T
n
/, however under the
additional nondegeneracy assumption on the function V .
Corollary IV.23. If M is a compact manifold and if V W M ! R is of class C
2
and possesses only nondegenerate critical points, then we have, for every 0 k
dim M , the inequality
m
k
m
k1
C m
k2
˙m
0
ˇ
k
ˇ
k1
C ˇ
k2
˙ˇ
0
:
Proof. Setting Q.t / D
P
t
j
q
j
, it follows from Theorem IV.20 by comparing the
coefficients of t
j
that
k
X
j D0
t
j
m
j
D
k
X
j D0
t
j
ˇ
j
C t
k
q
k
C .1 C t/
k1
X
j D0
t
j
q
j
:
Multiplication by t
k
leads to
k
X
j D0
t
j k
m
j
D
k
X
j D0
t
j k
ˇ
j
C q
k
C t
k
.1 C t/
k1
X
j D0
t
j
q
j
:
Setting t D1 and recalling that q
k
0, the corollary follows.
Next, we develop some preparatory steps for the proof of Theorem IV.20. First,
we shall show that the topological type of the sublevel set
M
a
´fx 2 M j V.x/ ag;a2 R
only changes when we pass a critical level, as illustrated in Figure IV.19 for the
2-torus. The compact set M
a
is a manifold having the boundary @M
a
D V
1
.a/,
if a is a regular value of V .Fora<bwe introduce the subset
M
b
a
´fx 2 M j a V.x/ bg:

170 Chapter IV. Gradientlike flows
V
R
2
Figure IV.19. The 2-torus with height function V , with the critical levels in bold print.
Proposition IV.24 (Deformation lemma). If V W M ! R is of class C
2
and if
a<band if
M
b
a
\ K D;;
then M
b
is diffeomorphic to M
a
. Moreover, the sublevel set M
a
is a strong
deformation retract of M
b
.
Corollary IV.25. Under the assumptions in the deformation lemma the cohomolo-
gies H
j
.M
b
;M
a
/ D 0 of the pair of spaces vanish for all j .
Proof [Borrowed from topology]. This follows because M
a
M
b
is a deforma-
tion retract of M
b
.
Proof of Proposition IV.24. The diffeomorphism will be constructed by means of
the gradient flow. We reparametrize the orbits of the gradient vector field Px D
rV.x/ and define the rescaled vector field
X.x/ ´˛.x/rV.x/; x 2 M;
with a non-negative differentiable function ˛ W M ! R satisfying on M
b
a
the equa-
tion
˛.x/ D
1
jrV.x/j
2
;x2 M
b
a
:
In view of the compactness there exists an ">0such that M
bC"
a"
\K D;. On the
open neighborhood V
1
.a "; b C"/ of M
b
a
, the vector field rV does not vanish.
The flow
t
on M , generated by the vector field X, satisfies
d
dt
t
.x/ D X.
t
.x//;
0
.x/ D x
