Zehnder E. Lectures on Dynamical Systems: Hamiltonian Vector Fields and Symplectic Capacities
Подождите немного. Документ загружается.


V.4. The Lie derivative L
X
of vector fields 201
Because L
X
.'
t
/
˛ D
d
dt
.'
t
/
˛
and because the Lie derivative L
X
is linear, it
follows that
d.H˛/ D .'
t
/
˛
ˇ
ˇ
ˇ
0
1
i
X
Z
0
1
.'
t
/
d˛ dt
:
Due to .'
0
/
D Id and .'
t
/
˛ ! 0 as t !1we obtain
d.H˛/ D ˛ H.d˛/:
Hence we arrive at the formula
d B H C H B d D Id
which holds true on
k
.V /.Ifd˛ D 0, then by the above formula, d.H˛/ D
˛ H.0/ D ˛ so that ˇ ´ H˛ is a solution of the equation dˇ D ˛ and the proof
is complete.
V.4 The Lie derivative L
X
of vector fields
If X is a vector field on an open set U R
n
and if '
t
is the flow of X , then '
t
is a
(local) diffeomorphism and the vector field Y on U can be transformed according
to the rule
.'
t
/
Y.x/ D
d'
t
.x/
1
Y.'
t
.x//:
The Lie derivative of Y with respect to X is defined as the vector field
L
X
Y.x/ ´
d
dt
.'
t
/
Y.x/
tD0
μ
Œ
X; Y
.x/:
The vector field ŒX; Y on the right-hand side is also called the Lie bracket of the
vector fields X and Y . Due to '
tCs
D '
t
B '
s
,
d
dt
.'
t
/
Y D
d
ds
.'
tCs
/
Y
ˇ
ˇ
ˇ
sD0
D .'
t
/
d
ds
.'
s
/
Y
ˇ
ˇ
ˇ
sD0
so that
d
dt
.'
t
/
Y D .'
t
/
ŒX; Y :
Proposition V.16. The Lie bracket Π; transforms naturally under a diffeomor-
phism u W R
n
! R
n
, that is,
Œu
X; u
YD u
ŒX; Y :

202 Chapter V. Hamiltonian vector fields and symplectic diffeomorphisms
Proof. If '
t
is the flow of X, then the transformed vector field u
X possesses
(Proposition IV.5) the flow
t
D u
1
B '
t
B u. We compute
.
t
/
.u
Y/D .d
t
/
1
.u
Y/B
t
D .du/
1
.d'
t
/
1
du.du/
1
Y B u B
t
D .du/
1
Œ.d'
t
/
1
Y B '
t
B u
D u
.'
t
/
Y:
Therefore,
d
dt
.
t
/
.u
Y/j
tD0
D u
d
dt
.'
t
/
Y j
tD0
D u
ŒX; Y :
The left-hand side is, by definition, equal to Œu
X; u
Y.
Proposition V.17. On R
n
the Lie bracket possesses the representation
ŒX; Y D d Y.X/ dX.Y /:
Proof. Let '
t
be the flow of X. The inverse invW A 7! A
1
on GL.R
n
/ has
the derivative d inv.A/B DA
1
BA
1
which follows from the Neumann series.
Using the product rule and the chain rule we compute
d
dt
Œ.d'
t
/
1
Y B'
t
D.d'
t
/
1
d
dt
.d'
t
/
.d'
t
/
1
Y B'
t
C.d'
t
/
1
dY.'
t
/
d
dt
'
t
:
Taking the derivative of
d
dt
'
t
D X.'
t
/ we obtain
d
dt
.d'
t
/ D dX.'
t
/d'
t
which, substituted into the above equation, gives
d
dt
Œ.d'
t
/
1
Y B '
t
D.d'
t
/
1
dX.'
t
/Y.'
t
/ C .d'
t
/
1
dY.'
t
/X.'
t
/
D .d'
t
/
1
ŒdY.X/ dX.Y / B '
t
:
Evaluating at t D 0, the proposition follows in view of '
0
D Id and d'
0
D 1 and
the proof is complete.
Corollary V.18. The Lie bracket satisfies ŒX; Y DŒY; X .

V.5. Commuting vector fields 203
V.5 Commuting vector fields
Two vector fields are said to commute, if their Lie bracket vanishes.
Proposition V.19. If X is a vector field having the flow '
t
, then .'
t
/
Y D Y for
all t if and only if ŒX; Y D 0.
Proof. We recall that
d
dt
.'
t
/
Y D .'
t
/
ŒX; Y :
If .'
t
/
Y D Y for all t , then the left-hand side vanishes and due to '
0
D Id we
obtain ŒX; Y D 0. Conversely, if ŒX; Y D 0, then
d
dt
.'
t
/
Y D 0 so that .'
t
/
Y
is constant in t . Hence .'
t
/
Y D .'
0
/
Y D Y for all t.
Two vector fields commute if and only if their flows commute.
Proposition V.20. If X and Y are vector fields having the flows '
t
and
t
, then
ŒX; Y D 0 is equivalent to
s
B '
t
D '
t
B
s
for all s; t.
Proof [Uniqueness of the flow, Proposition V.19]. We assume that
s
B'
t
D '
t
B
s
for all s and t . Differentiating both sides in t leads to
d
s
.'
t
/X.'
t
/ D X.'
t
B
s
/;
and we deduce for t D 0 the equation d
s
X D X B
s
, so that
X D .d
s
/
1
X B
s
D .
s
/
X
for all s. In view of Proposition V.19 the claim ŒX; Y D 0 follows.
Conversely, if ŒX; Y D 0, then .
s
/
X D X for all s according to Proposi-
tionV.19. Since '
t
is the flow of X, the flow of the transformed vector field .
s
/
X
is equal to
.
s
/
1
B '
t
B
s
for all t . Due to .
s
/
X D X it follows from the uniqueness of the flow that
.
s
/
1
B '
t
B
s
D '
t
and the proposition is proved.
V.6 The exterior derivative d on manifolds
Up to now we have dealt with the formalism of differential forms locally on open
sets of the Euclidian space. Globally on a manifold we shall glue our local objects
together by means of their transformation formulas based on the chart transforma-
tions. We consider a smooth manifold M of dimension dim M D n. We recall
that M is a Hausdorff topological space equipped with a maximal atlas of charts
.U; '/. The subsets U are open subsets which constitute a covering of the space
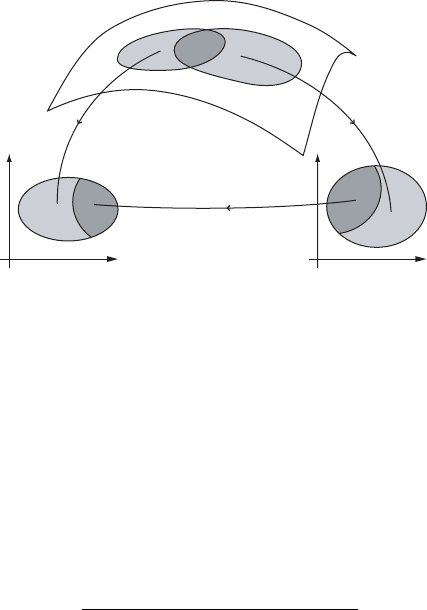
204 Chapter V. Hamiltonian vector fields and symplectic diffeomorphisms
M and the mappings ' W U ! '.U / R
n
are homeomorphisms. Moreover, if
two charts .U; '/ and .V; / overlap, so that U \V ¤;, then the associated chart
transformation is smooth, that is, the bijective mapping
' B
1
W .U \ V/ R
n
! '.U \ V/ R
n
is a C
1
-diffeomorphism between open sets of R
n
.
R
n
R
n
'
' B
1
U
V
U \V
Figure V.1. Manifold with the two charts .U; '/ and .V; /.
If T
m
M is the tangent space at the point m 2 M , every chart .U; '/ containing
m 2 U defines a canonical linear isomorphism
T
m
' W T
m
M ! R
n
:
Taking another such chart .V; / around m, the diagram
T
m
M
T
m
''
O
O
O
O
O
O
O
O
O
O
O
O
O
T
m
'
ww
o
o
o
o
o
o
o
o
o
o
o
o
o
R
n
R
n
.T
m
'/B.T
m
/
1
oo
is commutative and
T
m
' B .T
m
/
1
D d.' B
1
/. .m// 2 L.R
n
; R
n
/
is the linearized chart transformation. The coordinates x D '.m/ and y D .m/
in R
n
are related by x D ' B
1
.y/, and the two vectors v; w 2 R
n
satisfying
v D d.' B
1
/.y/w, represent the same tangent vector of T
m
M . In other words v
and w are the local coordinates of the same tangential vector in the different charts.
Note that the tangent spaces are isomorphic to R
n
, but have no canonical basis.
V.6. The exterior derivative d on manifolds 205
A k-form, 0 k n, on the manifold M is a smooth mapping
! W m 7! !.m/ 2
V
k
.T
m
M/; m 2 M
which associates with every point m the multilinear form !.m/.v
1
;:::;v
n
/ 2 R in
the tangent space at m. It is linear in every argument v
j
2 T
m
M and alternating.
In the chart .U; '/ the k-form ! is represented by the k-form !
'
2
k
.'.U //,
defined on the open set '.U/ R
n
by
!
'
.x/.v
1
;:::;v
k
/ ´ !.m/
ŒT
m
'
1
v
1
;:::;ŒT
m
'
1
v
k
;v
j
2 R
n
;
where x D '.m/ 2 R
n
. For this we can also write
.'
1
/
!.x/.v
1
;:::;v
k
/ ´ !
'
.x/.v
1
;:::;v
k
/:
The smoothness of the forms on the manifold is defined in the local coordinates as
follows. The k-form ! on the manifold M is smooth, if its representatives !
'
in the
charts .U; '/ are smooth k-forms on the open sets '.U/ R
n
. This requirement
is independent of the choice of the charts. Indeed, if !
is the representative of !
in the chart .V; /, then the transformation formula
!
'
D . B '
1
/
!
holds true on U \V , as is readily verified. Because, by definition, the chart transfor-
mation B'
1
is a smooth diffeomorphism, the smoothness of one representative
follows from the smoothness of the other one.
We also see that a k-form ! on the manifold can alternatively be defined by
smooth k-forms !
'
on the open sets '.U/ R
n
associated with the charts .U; '/,
which are compatible in the sense that on overlapping charts they meet the above
transformation formula.
We denote the set of k-forms on the manifold M by
k
.M /
Proposition V.21. There exists a unique R-linear map
d W
k
.M / !
kC1
.M /; k 0
having the following properties.
(i) If f 2
0
.M / is a smooth function, then df is the ordinary derivative.
(ii) d.! ^ / D d! ^ C .1/
k
! ^ d for ! 2
k
.M / and 2
l
.M /.
(iii) d
2
D 0.
(iv) d is a local operation; if U M is an open set and ! 2
k
.M / then
d!j
U
D d.!j
U
/.
(v) '
B d D d B '
for every smooth map ' W M ! N between manifolds.

206 Chapter V. Hamiltonian vector fields and symplectic diffeomorphisms
Proof. (1) Existence.If.U
˛
;'
˛
/ and .U
ˇ
;'
ˇ
/ are two charts satisfying U
˛
\U
ˇ
¤
;, then we abbreviatethe open subsets V
˛ˇ
D '
˛
.U
˛
\U
ˇ
/ and V
ˇ˛
D '
ˇ
.U
˛
\U
ˇ
/
of the R
n
as well as the chart transformation
'
˛ˇ
D '
˛
B '
1
ˇ
W V
ˇ˛
! V
˛ˇ
;
which is a diffeomorphism of open subsets of R
n
. On open subsets of R
n
we have
already defined the exterior derivative d above. We recall from Proposition V.11
the crucial fact that the pullback of forms and the exterior derivative d commute,
so that the diagram
k
.V
˛ˇ
/
d
'
˛ˇ
//
k
.V
ˇ˛
/
d
kC1
.V
˛ˇ
/
'
˛ˇ
//
kC1
.V
ˇ˛
/
is commutative. In formulas we have d.'
˛ˇ
!/ D '
˛ˇ
.d!/ for all forms ! 2
k
.V
˛ˇ
/ and so,
'
˛ˇ
1
B d B '
˛ˇ
D d:
Using this formula we shall define the exterior derivative d of the form ! 2
k
.M /
by means of the charts .U
˛
;'
˛
/ as follows:
.d!/j
U
˛
´ '
˛
B d B .'
1
˛
/
.!j
U
˛
/:
In order to verify that we have defined a global object, we have to show that the
definition is independent of the choice of the charts. To do so we compute, on
U
˛
\ U
ˇ
,
d!j
U
˛
\U
ˇ
D '
˛
B d B .'
1
˛
/
.!j
U
˛
\U
ˇ
/
D '
˛
B '
˛ˇ
1
B d B '
˛ˇ
B .'
1
˛
/
.!j
U
˛
\U
ˇ
/
D .'
˛ˇ
1
B '
˛
/
B d B .'
˛
1
B '
˛ˇ
/
.!j
U
˛
\U
ˇ
/
D '
ˇ
B d B '
1
ˇ
.!j
U
˛
\U
ˇ
/:
Hence we have defined a .k C1/-form d! on M , which possesses the properties
(i)–(v), as we already know from the chart representations.
(2) Uniqueness. The proof of the uniqueness of d is left as an exercise. It can
be found, for example, in [21, Theorem 8.1.6] by L. Conlon.
V.7 Symplectic manifolds
Definition. A symplectic manifold is a pair .M; !/ consisting of a smooth manifold
M of dimension dim M D 2n and a symplectic structure !. A symplectic structure
is a 2-form ! on M having the following two properties:
V.7. Symplectic manifolds 207
(i) ! is nondegenerate,
(ii) ! is closed, i.e., d! D 0.
The differential form ! is called nondegenerate, if in every point x 2 M the
2-form !.x/ on the tangent space T
x
M is nondegenerate, i.e., !.x/.u; v/ D 0 for
all v 2 T
x
M implies u D 0. Equivalently, the map u 7! !.x/.u; / from the
tangent space T
x
M onto its dual space .T
x
M/
is a linear isomorphism.
By definition, every tangent space
T
x
M; !.x/
is a symplectic vector space. A
first example for a symplectic manifold is the pair .U; !
0
/ in which U R
2n
is an
open set and !
0
is the standard symplectic structure on R
2n
. Actually this is what
every symplectic manifold looks like locally, according to the following theorem
of Darboux.
Theorem V.22 (Darboux). If ! is a nondegenerate 2-form on the manifold M of
dimension dim M D 2n, then d! D 0 if and only if there exists around every point
p 2 M a chart .U; '/ satisfying '.p/ D 0 2 R
2n
and
!j
U
D '
!
0
;
where !
0
D
P
n
j D1
dy
j
^dx
j
is the constant symplectic standard structure on R
2n
.
Definition. These special coordinates are called symplectic coordinates or Darboux
coordinates. A chart .U; '/ on which !j
U
D '
!
0
is called a Darboux chart.
In view of Darboux’s theorem we do not have to look for local invariants!
Corollary V.23. Two symplectic manifolds of the same dimension have locally the
same normal form, namely .R
2n
;!
0
/. They are therefore locally indistinguish-
able: Symplectic manifolds do not possess local symplectic invariants except the
dimension!
The situation is completely different from Riemannian manifolds. Two Rie-
mannian metrics are in general not locally isometric. The Gauss curvature is an
example of a local invariant.
Proof of Theorem V.22 [Deformation trick by R. Thom and J. Moser, Cartan’s
formula, Poincaré lemma]. We first assume that the nondegenerate 2-form is closed
so that d! D 0. In local coordinates ! D !.z/ is a nondegenerate 2-form on R
2n
,
which depends on the point z 2 R
2n
. By a translation we may assume that the
point p in M corresponds to z D 0, and by a linear transformation of R
2n
we can
achieve, in view of Proposition V.2 , that in the point z D 0 the 2-form is already in
normal form,
!.0/ D !
0
D
n
X
j D1
dy
j
^ dx
j
:

208 Chapter V. Hamiltonian vector fields and symplectic diffeomorphisms
We are looking for a local diffeomorphism ' around 0 satisfying
'.0/ D 0 and '
! D !
0
:
Using the deformation trick we are looking for more. We interpolate between
! and !
0
by the family of 2-forms
!
t
D !
0
C t.! !
0
/; 0 t 1;
so that !
t
D !
0
if t D 0 and !
t
D ! if t D 1. By assumption, d!
t
D 0 for all t .
We look for a family '
t
, 0 t 1 of local diffeomorphisms leaving the origin
fixed and satisfying
./
´
.'
t
/
!
t
D !
0
;0 t 1;
'
0
D Id :
Then the time 1 map '
1
of the family is the desired local diffeomorphism.
To determine the family '
t
we look for a time dependent vector field X
t
, which
generates the flow '
t
such that
d
dt
'
t
D X
t
.'
t
/; '
0
D Id :
Differentiating the identity ./ in the variable t and using Cartan’s formula we find
0 D
d
dt
Œ.'
t
/
!
t
D
d
dt
.'
t
/
!
t
C .'
t
/
d
dt
!
t
D .'
t
/
Œ
L
X
t
!
t
C ! !
0
D .'
t
/
Œ
d.i
X
t
!
t
/ C i
X
t
.d!
t
/ C ! !
0
D .'
t
/
Œ
d.i
X
t
!
t
/ C ! !
0
:
We have used that d!
t
D 0. Therefore, the vector field X
t
has to satisfy the linear
equation
d.i
X
t
!
t
/ C .! !
0
/ D 0:
By assumption, d.! !
0
/ D d! d!
0
D 0 and hence in view of the Poincaré
lemma there exists locally around 0 a 1-form satisfying
! !
0
D d and .0/ D 0:
Since !
t
.0/ D !
0
for all t, the 2-forms !
t
.z/ are nondegenerate for all t in a
neighborhood of z D 0. Therefore, there exists a unique time dependent vector
field X
t
, solving the equation
i
X
t
!
t
D !
t
.X
t
; / D:

V.8. Symplectic maps 209
Consequently,
0 D d.i
X
t
!
t
/ C d D d.i
X
t
!
t
/ C ! !
0
and we have found the desired vector field. From .0/ D 0 we conclude that
X
t
.0/ D 0, since !
t
is nondegenerate. We therefore find an open neighborhood
of z D 0, on which the flow '
t
of the vector field X
t
exists for all 0 t 1.It
satisfies '
0
D Id and '
t
.0/ D 0. Reversing now all our steps, this flow satisfies
d
dt
.'
t
/
!
t
D 0; 0 t 1
and therefore
.'
t
/
!
t
D .'
0
/
!
0
D !
0
;0 t 1:
Due to ! D !
1
the time 1 map of the flow is the desired diffeomorphism solving
.'
1
/
! D !
0
and '
1
.0/ D 0.
Conversely, assuming that '
! D !
0
, we conclude d! D d.'
.!
0
// D
'
.d!
0
/ D '
.0/ D 0 so that the 2-form ! is closed. This completes the proof of
Darboux’s theorem.
V.8 Symplectic maps
Definition. A smooth map u W M
1
! M
2
between two symplectic manifolds
.M
1
;!
1
/ and .M
2
;!
2
/ is called symplectic,if
u
!
2
D !
1
:
Explicitly,
!
2
.u.x//
du.x/v
1
; du.x/v
2
D !
1
.x/.u; v/; x 2 M
1
;u;v2 T
x
M
1
:
Consequently, the derivative du.x/W T
x
M
1
! T
u.x/
M
2
is a symplectic linear map
from the symplectic vector space
T
x
M
1
;!
1
.x/
into the symplectic vector space
T
u.x/
M
2
;!
2
.u.x//
for every x 2 M
1
.
Recalling the linear symplectic mappings in Section VI.1, we conclude from
the nondegeneracy of !
1
that a symplectic map is an immersion and
dim M
1
dim M
2
if there exists a symplectic map u W M
1
! M
2
.
210 Chapter V. Hamiltonian vector fields and symplectic diffeomorphisms
A differentiable map u W M ! M on a symplectic manifold .M; !/ is called
symplectic, if it leaves the symplectic form invariant, that is, if
u
! D !:
In the symplectic coordinates .U; '/ this is equivalent to the requirement that the
linearized map du.x/ 2 Sp.n/ is a symplectic matrix for every x 2 '.U / R
2n
,
so that
du.x/
T
J du.x/ D J;
where J is the matrix
J D
0 1
1 0
:
In particular, u is a local diffeomorphism.
We see that a symplectic map satisfies a special nonlinear partial differential
equation of first order. It allows us to give another equivalent definition of a sym-
plectic manifold.
Definition. We assume M to be a manifold of dimension dim M D 2n.Asym-
plectic structure on M is a covering of M consisting of charts .U
˛
;'
˛
/
˛2A
,
'
˛
W U
˛
! R
2n
;˛2 A;
whose chart transformations
'
˛ˇ
D '
˛
B '
1
ˇ
W '
ˇ
.U
˛
\ U
ˇ
/ ! '
˛
.U
˛
\ U
ˇ
/
are all symplectic local diffeomorphisms in .R
2n
;!
0
/ and hence satisfy d'
˛ˇ
.x/ 2
Sp.n/, or equivalently
'
˛ˇ
!
0
D !
0
;˛;ˇ2 A:
Proof of the equivalence of the definitions. For a symplectic structure .U
˛
;'
˛
/
˛2A
on M we define the 2-form !
˛
on U
˛
by
!
˛
´ '
˛
!
0
:
In this way we define a global 2-form ! on M , since on U
˛
\ U
ˇ
we have
!
˛
D '
˛
!
0
D .'
˛
B '
1
ˇ
B '
ˇ
/
!
0
D '
ˇ
B .'
˛
B '
1
ˇ
/
!
0
D '
ˇ
!
0
D !
ˇ
:
Because !
0
is nondegenerate and because d'
˛
.x/ is a bijective linear map,
the 2-form ! is nondegenerate. Moreover, ! is closed, since d!
˛
D d.'
˛
!
0
/ D
'
˛
.d!
0
/ D 0 so that ! is a symplectic form on M and .M; !/ is a symplectic
manifold. The other direction of the equivalence follows from Darboux’s theorem.
