Zehnder E. Lectures on Dynamical Systems: Hamiltonian Vector Fields and Symplectic Capacities
Подождите немного. Документ загружается.


III.4. Existence of transversal homoclinic points 111
0
x
y DPx
.a/
.b/
.c/
2
Figure III.12. Types in the unperturbed case.
Theorem III.19. Let U R
2
be an open neighborhood of the separatrix (in the
case D 0).Ifjj >0is sufficiently small, then there exists for every two-
sided sequence .s
k
/
k2Z
of integers s
k
2f1; 1g a solution x.t/ of the perturbed
pendulum equation RxCsin x D sin !t such that .x.t/; Px.t// 2 U which possesses
infinitely many nondegenerate zeros (mod 2) satisfying
k
.x.t// D s
k
;k2 Z:
In addition, for every finite sequence s
k
2f1; 1g where N k M there
exists a solution x.t/ possessing only finitely many nondegenerate zeros (mod 2)
and solving the equations
k
.x.t// D s
k
for N k M . The same applies to
half finite sequences s
k
for 1 <k M or for N k<1.
In short, one can prescribe any sequence of directions with which the pendulum
should consecutively pass through the lowest point and there exists a solution doing
precisely that.
Proof [Transversal heteroclinic point, shadowing lemma]. Assuming ¤ 0,we
consider the diffeomorphism of R
2
, defined by the time T flow map
.z; / ´
.z/ ´ '
T
.z; /;
at the time T D 2=! > 0. In the case D 0, the map has the hyperbolic fixed
point P ´ P
1
D .; 0/. We shall show that also the diffeomorphism
has a
unique hyperbolic fixed point P ./ near P D P .0/, which depends differentiably
on ,if is small enough. For this, we define the mapping F W R
2
R ! R
2
by
F.z;/ D '
T
.z; / z:

112 Chapter III. Hyperbolic sets
If D 0 then F.P;0/ D
T
.P; 0/ P D 0 and the partial derivative in the
variable z is given by
D
1
.P; 0/ D D
1
'
T
.P; 0/ 1 2 L.R
2
/:
The linear mapping D
1
F.P;0/is an isomorphism, since the hyperbolic matrix
D
1
'
T
.P; 0/ does not have an eigenvalue equal to 1. In a neighborhood of D 0
there exists, by the implicit function theorem, a unique continuously differentiable
function 7! P ./ 2 R
2
, solving F .P./; / D 0 and P .0/ D P . In other
words,
P ./ D
.P .//
is a fixed point of the mapping
. The eigenvalues of the derivative d
.P .//
depend continuously on , hence the linear map d
.P .// possesses for small
an eigenvalue whose absolute value is >1and an eigenvalue whose absolute
value is <1. Consequently, P ./ is a hyperbolic fixed point of
,if is small.
Also the points P ./ C 2n are hyperbolic fixed points and P ./ C 2n D
P
1
./ C 2n D P
n1
./.
From the proof of Theorem II.8 (construction of h) we know that the local
invariant manifolds issuing from the hyperbolic fixed point P ./, denoted by
W
˙
loc
.P .//;
depend differentiably on (by the implicit function theorem). For small they
can, therefore, be represented locally as graphs over the invariant manifolds of the
unperturbed system (the branches of the separatrix). If t 7! .t/ is a heteroclinic
solution in the unperturbed case D 0 having the x-coordinate at time t D 0 equal
to ..0//
1
D 0, then .t/ lies on the separatrix. In formulas,
d
dt
.t/ D X.0; .t//; t 2 R;
and .t/ ! P D P
1
as t !1and .t/ ! P C 2e
1
D P
0
as t !C1.
Denoting by n..t// the unit normal vector of the homoclinic orbit in the
point .t/ as depicted in Figure III.14, we can represent the relevant pieces of the
invariant manifolds as follows:
f.r/ C u
.r; / n..r// j1<r M gW
.P
1
.//
and
f.r/ C u
C
.r; / n..r// jM r<1g W
C
.P
0
.//;
with a sufficiently large constant M>0and where in the case D 0 the functions
u
C
.r; 0/ D u
.r; 0/ D 0 vanish.
If for a parameter value r 2 R,
u
.r; / D u
C
.r; / and
@
@r
u
.r; / ¤
@
@r
u
C
.r; /;

III.4. Existence of transversal homoclinic points 113
0
x
y
b
a
c
Legend: a: .M/ b: .0/ c: .M/ d: .r/
P
1
.0/
P
0
.0/
P
1
./
P
0
./
n..r//
d
W
C
.P
0
.//
W
.P
1
.//
Figure III.13. The perturbed invariant manifolds possessing a transversal intersection.
then we have found the transversal intersection point
´ .r/ C u
.r; / n..r// 2 W
.P
1
.// \ W
C
.P
0
.//:
In order to study the first-order term in of the function .u
u
C
/ we introduce
the so-called Melnikov function
d.r/ ´
@
@
.u
u
C
/j
D0
.r/:
If d.r
0
/ D 0 and
d
dr
d.r
0
/ ¤ 0, then there exists a transversal intersection point
near .r
0
/, for small ¤ 0. This follows from
.u
u
C
/.r; / D
d.r/ C O./
in view of the implicit function theorem. The first approximation d.r/ can be
explicitly calculated by means of the following Melnikov formula.
Theorem III.20 (Melnikov). Let
Pz D f.z/C g.t; z/ 2 R
2
;
z 2 R
2
be a smooth vector field satisfying div f D 0, where g is a T -periodic
vector field for some T>0, so that g.t C T;z/ D g.t; z/. We assume that for
D 0 there exists a homoclinic (resp. heteroclinic) orbit of the vector field f ,
hence satisfying
d
dt
.t/ D f..t//for all t 2 R and
.t/ ! P; t !1;
.t/ ! Q; t !C1
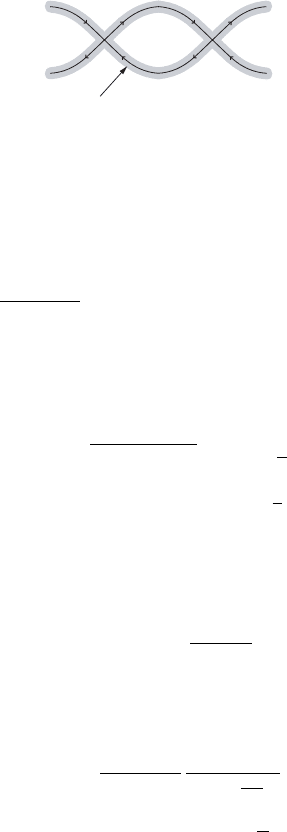
114 Chapter III. Hyperbolic sets
U
Figure III.14. A neighborhood U of the separatrix.
for two hyperbolic fixed points P and Q of f . Then, setting f D .f
1
;f
2
/ and
g D .g
1
;g
2
/ the following formula holds true:
d.r/ D
1
jf..r//j
Z
1
1
.f
1
g
2
f
2
g
1
/.s; .r C s// ds:
For a proof we refer to C. Robinson in [91, S. 304]. In order to apply the formula
to our pendulum, we consider the upper branch of the unperturbed separatrix,
´
x ;
y DC
p
2.1 C cos x/ D 2 cos.
x
2
/
where y DPx. The solution of the equation Px D 2 cos.
x
2
/ is given by
x.t/ D 2 arcsin.tanh.t//; t 2 R;
and differentiating we obtain
Px.t/ D y.t/ D
2
cosh.t /
:
Hence .t/ D .x.t/; y.t// is the heteroclinic orbit. Inserting the curve into
the Melnikov formula results in
d.r/ D
1
jX..r//j
2 sin.!r/
cosh.
!
2
/
:
The function d.r/ has the nondegenerate zeros r D
!
j for all j 2 Z. Therefore,
there exists a transversal heteroclinic point . In the same way, there exists near the
lower branch of the separatrix a transversal heteroclinic point . The closure of the
heteroclinic orbits is the hyperbolic set
ƒ D
[
j;k2Z
j
. C 2ke
1
/ [fP
k
./g[
j
. C 2ke
1
/:
In order to finish the proof of Theorem III.19 we choose a neighborhood U of
the separatrix and we choose the parameters "; ı as in the shadowing lemma. For the

III.4. Existence of transversal homoclinic points 115
given sequence s D .s
k
/
k2Z
we construct the following "-pseudo orbit q, described
by Figure III.15.Ifs
0
D 1, we start in the heteroclinic point q
0
D and if s
0
D1
we start in the heteroclinic point q
0
D . Then we follow the heteroclinic orbit
j
./, resp.
j
./ into the ."=2/-neighborhood of the next hyperbolic fixed point.
There one has again two possibilities. If s
1
D 1 we jump onto the heteroclinic orbit
of the upper branch to the right while if s
1
D1 we jump onto the heteroclinic
orbit of the lower branch to the left, and so on.
P
1
./
P
0
./
P
1
./
Figure III.15. The "-pseudo orbit associated with the sequence .s
k
/D.:::;s
0
;s
1
;s
2
;:::/D
.:::;1;1;1;:::/.
The associated ı-shadowing orbit p D .p
j
/
j 2Z
guaranteed by the shadowing
lemma,
p
j
D
j
.p
0
/ D '
jT
.p
0
; /; j 2 Z;
lies on the desired solution t 7! '
t
.p
0
;/of the perturbed vector field X.t; ; z/
starting at the point '
0
.p
0
;/ D p
0
at the time t D 0 and remaining in the open
neighborhood U of the separatrix. Of course, this solution loses a lot of time near
the hyperbolic equilibrium points, away from these neighborhoods it moves quite
fast. We point out that all the solutions found this way start in a small neighborhood
of the homoclinic points resp. !
The passages near the transversal heteroclinic points resp. correspond to the
passages of the pendulum through the point x D 0 mod 2, which is the lowest
position of the pendulum. In order to obtain a solution defined by a finite sequence
.s
k
/, one constructs an "-pseudo orbit q as before which, however, at the ends is
equal to the orbits of hyperbolic fixed points. Then, the corresponding solution of
the pendulum equation makes finitely many swings back and forth and then remains
almost immobile near the highest position of the pendulum! This completes the
proof of Theorem III.19.
For a detailed study of the chaotic behavior of the periodically perturbed pen-
dulum we refer to U. Kirchgraber and D. Stoffer in [59].
116 Chapter III. Hyperbolic sets
III.5 Torus automorphisms
A diffeomorphism of a compact Riemann manifold that is a hyperbolic set for the
diffeomorphism is called an Anosov diffeomorphism. In contrast to our previous
studies of transversal homoclinic orbits of a hyperbolic fixed point, the hyperbolic
structure is postulated for an Anosov diffeomorphism. Hyperbolic torus automor-
phisms are a standard example of a hyperbolic system on a compact manifold.
We describe a simple but typical example on the 2-torus T
2
D S
1
S
1
whose
covering space is R
2
. The covering map
p W R
2
! T
2
;.x
1
;x
2
/ 7! .e
2ix
1
;e
2ix
2
/;
satisfies p.x C !/ D p.x/ for all ! 2 Z
2
. Clearly, T
2
Š R
2
=Z
2
. We consider
the linear mapping
A D
21
11
2 L.R
2
/:
Then det A D 1, and the matrix elements of the inverse map
A
1
D
1 1
12
are also integers. In particular, A.Z
2
/ D Z
2
and A
1
.Z
2
/ D Z
2
. Consequently,
A induces the mapping '
A
on the torus given by
'
A
.e
2ix
1
;e
2ix
2
/ D
e
2i.2x
1
Cx
2
/
;e
2i.x
1
Cx
2
/
:
This map is a diffeomorphism of T
2
, having the inverse mapping
'
1
A
D '
A
1
W .e
2ix
1
;e
2ix
2
/ 7!
e
2i.x
1
x
2
/
;e
2i.x
1
C2x
2
/
:
In view of '
A
B p D p B A the diagram
T
2
'
A
//
T
2
R
2
A
//
p
OO
R
2
p
OO
is commutative.
We note that if A; B belong to the group SL
2
.Z/ of the .2 2/ matrices having
determinants equal to 1 and integer matrix elements, then
'
A
B '
B
D '
AB
;'
1
A
D '
A
1
;'
1
D Id
T
2
:
We next consider the linear map in the covering space R
2
. The matrix A is
symmetric and has the eigenvalues 0<
1
<1<
2
,
1
D
3
p
5
2
;
2
D
1
1
D
3 C
p
5
2
:

III.5. Torus automorphisms 117
The corresponding orthogonal eigenvectors are the vectors
v
1
D
1
p
5C1
2
!
;v
2
D
1
p
5C1
2
!
;
satisfying Av
1
D
1
v
1
and Av
2
D
2
v
2
. Therefore, the origin 0 is a hyperbolic
fixed point of the map AW R
2
! R
2
possessing the invariant splitting R
2
D E
C
˚
E
, defined by the eigenspaces
E
C
Dftv
1
j t 2 Rg and E
Dftv
2
j;t 2 Rg:
Clearly,
A
j
x
C
D
j
1
x
C
;x
C
2 E
C
;
A
j
x
D
j
2
x
;x
2 E
:
The image of the fixed point 0 under the projection mapping,
p.0/ D 0
2 T
2
;
is a hyperbolic fixed point of the diffeomorphism '
A
W T
2
! T
2
, since in suitable
local coordinates the derivative is equal to d'
A
.0
/ D A.
From '
A
Bp D p B A it follows that '
j
A
Bp D p B A
j
. Hence '
j
A
.p.x// ! 0
as j !˙1, precisely if A
j
x ! 0 mod Z
2
as j !˙1, hence precisely
if x 2 E
C
resp. x 2 E
. The stable and unstable manifolds issuing from the
hyperbolic fixed point 0
are therefore the curves
W
C
.0
;'
A
/ D p.E
C
/;
W
.0
;'
A
/ D p.E
/:
These immersed curves are dense on T
2
. Indeed, since hv
1
;ji…Z for all
0 ¤ j 2 Z
2
, already the set fp.nv
1
/ j n 2 Ng is dense in T
2
in view of
Corollary I.7 (Kronecker). The same argument applies to the unstable manifold
p.E
). The homoclinic points W
C
.0
;'
A
/ \ W
.0
;'
A
/ n 0
are also dense in
T
2
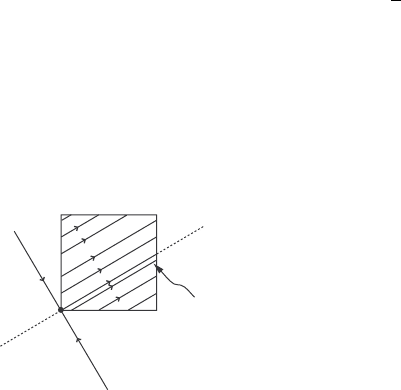
and transversal. This is obvious, if we look at the invariant manifolds in the
fundamental domain Œ0; 1
2
of T
2
(Figure III.16).
Proposition III.21. The diffeomorphism '
A
W T
2
! T
2
has the following proper-
ties.
(i) '
A
is hyperbolic.
(ii) '
A
is ergodic in relation to the Lebesgue measure m.
(iii) The set R
C
Dfx 2 T
2
j O
C
.x/ D T
2
g of points with dense positive semi
orbit has full measure m.R
C
/ D m.T
2
/, is dense on T
2
and of second Baire
category.
118 Chapter III. Hyperbolic sets
(iv) The periodic points are countable and dense. They are the points p.
1
k
j/for
k 2 N and j 2 Z
2
.
(v) The transversal homoclinic points belonging to the hyperbolic fixed point 0
are dense.
(vi) The diffeomorphism '
A
is structurally stable.
We see that every open subset of T
2
contains points whose orbits behave in the long
run completely differently under the diffeomorphism '
A
.
0
E
C
E
1
1
Figure III.16. E
in the fundamental domain of the torus.
Proof. (i) The torus T
2
is compact. At the point p 2 T
2
we have d'
A
.p/ D A in
suitable local coordinates so that the desired splitting is defined by the eigenspaces
of A.
(ii) We shall show that every invariant function f 2 L
1
.T
2
/ is constant almost
everywhere. The lift F W R
2
! C of the function f W T
2
! C is defined by
F.x
1
;x
2
/ D f.e
2ix
1
;e
2ix
2
/:
If the function f is invariant, that is, f D f B'
A
, then also F D F BA is an invariant
function. We calculate the Fourier coefficients f
k
for k 2 Z
2
of F . Let A
T
be the
transposed of A and j 2 Z
2
.Fork D A
T
j we obtain, using the invariance of the
function F and jdet AjD1,
f
A
T
j
D
Z
F.x/e
2ihA
T
j;xi
dx
D
Z
F.x/e
2ihj;Axi
dx
D
Z
F .Ax/e
2ihj;Axi
dx
D
Z
F.y/e
2ihj;yi
dy
D f
j
:

III.5. Torus automorphisms 119
This holds true for every j 2 Z
2
and setting B ´ A
T
, we therefore deduce
f
j
D f
Bj
D f
B
2
j
DDf
B
n
j
D;j2 Z
2
:
For f belonging to L
1
we know that
f
k
! 0; jkj!1;
where jkjD
q
k
2
1
C k
2
2
. Hence, if the sequence jB
n
j j for every fixed 0 ¤ j 2 Z
2
is unbounded, then f
j
D 0 for all j ¤ 0 and consequently the function f is
constant almost everywhere.
The sequence jB
n
j j is indeed unbounded, because the set fB
n
j j n 2 Ng is
an infinite set, since for j ¤ 0 all these points are different. If they were not, we
would find an integer m 2 N satisfying B
m
j D j , so that B
m
would have an
eigenvalue 1. This, however, is not possible, since B and hence B
m
is a hyperbolic
map. We have demonstrated that every invariant integrable function is constant
almost everywhere. Consequently, due to Proposition I.17 the diffeomorphism '
A
is ergodic.
(iii) The statement (iii) follows from the ergodicity of '
A
(Proposition I.21).
(iv) Since A is an invertible matrix over the ring Z,wehaveA.Z
2
/ D Z
2
, hence,
due to the linearity A.
1
k
Z
2
/ D
1
k
Z
2
. On the torus we conclude '
A
.p.
1
k
Z
2
// D
p.A.
1
k
Z
2
// D p.
1
k
Z
2
/. This set is finite (since it corresponds bijectively to the set
Œ0; 1/ Œ0; 1/ \
1
k
Z
2
), hence '
A
is a permutation of this set and the orbits in
1
k
Z
2
are all periodic. The points p.
1
k
Z
2
/ with k 2 N lie densely on the torus. We claim
that we have found already all the periodic points. Indeed, if p.z/ is a periodic
point of '
A
, where z D .x; y/ 2 R
2
, then there exist an integer n and an integer
vector k D .k
1
;k
2
/ 2 Z
2
such that A
n
z D z Ck and hence .A
n
1/z D k. Since
A
n
does not have an eigenvalue 1, this equation has a unique solution z D .x; y/,
given by a rational function of the integer matrix elements of A
n
and of k
1
;k
2
and
therefore x; y 2 Q are rational, as claimed.
(v) The statement (v) has been proved previously.
(vi) We assume that g is a C
1
perturbation of '
A
, so that g D '
A
COg where
the map Og is small in the C
1
-sense. We consider the homotopy g
t
D '
A
C t Og,
connecting g
0
D '
A
with g
1
D g and we choose a lift G of the end point g D g
1
,
so that G.0/ is near 0. We then lift the homotopy to a homotopy G
t
. We may
assume that G
0
D A. From
G
0
.x C j/ G
0
.x/ D A.x C j/ Ax D Aj 2 Z
2
;z2 Z
2
it follows, since Z
2
R
2
is discrete, that
G
t
.x C j/ G
t
.x/ D Aj 2 Z
2
120 Chapter III. Hyperbolic sets
for every t 2 Œ0; 1. In particular also for t D 1 and we set G
1
D G. The mapping
y
G ´ G A satisfies
y
G.x C j/ D
y
G.x/; j 2 Z
2
and therefore
j
y
Gj
C
0
D sup
x2Œ0;1
2
jG.x/j < 1:
Assuming kd Ogk" we obtain the Lipschitz estimate
j
y
G.x/
y
G.y/j"jx yj:
We can therefore apply the arguments of the proof of Theorem II.4 to the map-
ping G D A C
y
G, replacing the space X D C
b
.R
n
; R
n
/ by the space of periodic
mappings X
0
D C
per
.R
n
; R
n
/,
C
per
.R
n
; R
n
/ ´ C.R
n
; R
n
/ \ff W R
n
! R
n
j f.x C j/ D f.x/; j 2 Z
n
g:
Arguing as in Theorem II.4 we find a homeomorphism H of R
2
of the form
H D Id Cv with v 2 C
per
.R
2
; R
2
/ which solves the equation
G B H D H B A:
In view of H D Id Cv we have for j 2 Z
2
,
H.x C j/ D x C j C v.x C j/ D x C j C v.x/ D H.x/ C j;
so that H induces a continuous and surjective map h W T
2
! T
2
solving
g Bh D h B '
A
:
In order to prove the injectivity of the map h we assume that h.p.x// D h.p.y//.
Then H.x/ D H.y/ C j for an integer vector j 2 Z
2
and recalling H.y/ C j D
H.y Cj/we obtain H.x/ D H.y Cj/. Due to the injectivity of H we conclude
x D yCj and hence p.x/ D p.yCj/ D p.y/. Finally, in viewof the compactness
of T
2
the map h is a homeomorphism and we have verified that the diffeomorphism
'
A
is indeed structurally stable.
We would like to remark that, more generally, a hyperbolic .n n/-matrix A
with integer matrix elements and satisfying det A D˙1 induces a diffeomorphism
'
A
on the torus T
n
D R
n
=Z
n
which also has the properties of Proposition III.21.
Such a mapping '
A
is called a hyperbolic torus automorphism. It turns out that
every Anosov diffeomorphism of the torus T
n
is topologically conjugated to such
a hyperbolic torus automorphism '
A
, for details we refer to the book [49, p. 587]
by B. Hasselblatt and A. Katok.
