Zehnder E. Lectures on Dynamical Systems: Hamiltonian Vector Fields and Symplectic Capacities

Подождите немного. Документ загружается.

III.6. Invariant manifolds of ƒ 121

Remark. In the ergodic theorem criterion (Theorem I.18) we have seen the fol-

lowing. If ' is an ergodic transformation of a ﬁnite measure space, then for every

integrable function f the mean value over an orbit is equal to the mean value over

the whole space, so that f



.x/ D

f , or explicitly,

lim

n!1

n1

j D0

f.'

x/ D

m.X/

for almost every x. In general, this equation does not hold true for all points x,as

for example a ﬁxed point of ' shows.

We will show next that f



.x/ D

f can fail even on a dense subset of a topo-

logical measure space.Looking at the above torus automorphism ' D '

on T

equipped with the (normalized) Lebesgue measure and taking the continuous map

f W T

! R, deﬁned by

f.e

2ix

/ ´ e

2ix

;

we see that the mean value over the space vanishes,

f D

2ix

D 0:

We claim that for every x 2 W



/ nf0



lim

n!1

n1

j D0

f.'

x/ D 1;

so that f



.x/ D 1. In order to prove this claim we ﬁrst observe that, in view of

the deﬁnition of the stable invariant manifold W

and using the continuity of f ,

we have f.'

x/ ! f.0



/ D 1. The claim now follows from the fact that for a

converging sequence of numbers a

! 0, also the sequence of means

n1

j D0

converges to 0.

III.6 Invariant manifolds of ƒ

We would like to describe, without giving proofs, the generalization of the invariant

manifolds issuing from a hyperbolic ﬁxed point to the above situation of a hyperbolic

set ƒ  R

. It turns out that the subset of points in R

, which under the forward

iterates lie near an orbit q on ƒ, form a local manifold called the local stable

manifold of the orbit q. Similarly, the set of points that remain close to the orbit q

on ƒ under the backward iterates form the local unstable manifolds of the orbit q.

Actually, this holds true even for an "-pseudo orbit q on the hyperbolic set ƒ.

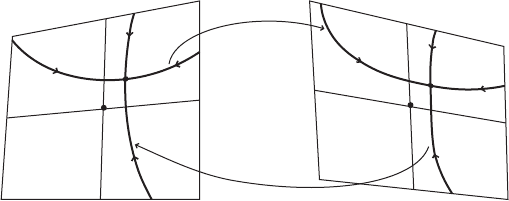
122 Chapter III. Hyperbolic sets

1

loc



loc



loc

Figure III.17. Invariance of the local invariant manifolds.

We focus on the "-pseudo orbit q of the diffeomorphism ' on ƒ and deﬁne for

ı>0the sequence of neighborhoods

Dfx 2 R

jjx  q

jıg;j2 Z

containing the subsets of R

loc

/ Dfx 2 Q

j '

.x/ 2 Q

j Ck

for all k  0g;



loc

/ Dfx 2 Q

j '

k

.x/ 2 Q

j k

for all k  0g;

for j 2 Z. Clearly, these sets are ˙ invariant in the sense that

'.W

loc

//  W

loc

j C1

1



loc

//  W



loc

j 1

We abbreviate the splittings in Tƒ D T R

and simply write

˚ E



´ E

˚ E



D T

ƒ D R

If ı>0is sufﬁciently small, then there exists an " D ".ı/ > 0 such that for

every "-pseudo orbit q D .q

/ of the diffeomorphism ' on ƒ the following holds

true:

loc

/ Df.x

/ 2 .E

˚ E



/ \ Q



loc

/ Df.h



/; x



/ 2 .E

˚ E



/ \ Q

for every j 2 Z, where the maps h

W E

! E



are of class of C

,if' is of class

. The analogous statement holds true for the maps h



W E



! E

. Moreover,

loc

/ \ W



loc

/ μfp

g for all integers j 2 Z;

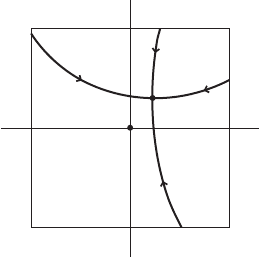
III.6. Invariant manifolds of ƒ 123

and p

D '

/, j 2 Z is the ı-shadowing orbit of the "-pseudo orbit q. If, in

particular, q D p is an orbit of the diffeomorphism ' on the hyperbolic set ƒ,we

have, in addition,

(i) W

loc

/ \ W



loc

/ Dfp

(ii) T

loc

/ D E

for the tangent spaces,

(iii) W

loc

/ Dfx 2 Q

jj'

.x/  p

j Cn

j!0; n !1g,

(iv) W



loc

/ Dfx 2 Q

jj'

n

.x/  p

j n

j!0; n !1g.

We see that the bounds imply the convergence, as before.

loc



loc



Figure III.18. Intersection of W

loc

/ and W



loc

We leave the proofs of these statements as an exercise to the reader with the

hint that one combines the proof of Theorem II.8 with the shadowing lemma, the

contraction principle, and the implicit function theorem. For proofs of these state-

ments, known under the names stable manifold theorem and Hadamard–Perron

theorem we refer, for example, to the books [49, S. 242, S. 267] by B. Hasselblatt

and A. Katok, [103, S. 71] by M. Shub, [91, S. 411] by C. Robinson.

The global invariant manifolds of the points p

D '

/ of an orbit on ƒ are

the following subsets of R

/ D

[

n0

n

loc

//;



/ D

[

n0



loc

//:

The unions W

.p/ D

j 2Z

/ and W



.p/ D

j 2Z



/ are the

global invariant manifolds of the orbit p D .p

/. These sets are characterized by

124 Chapter III. Hyperbolic sets

the following properties,

.p/ Dfx 2 R

j d.p

.x// ! 0; j !1g;



.p/ Dfx 2 R

j d.p

j

.x// ! 0; j !1g:

III.7 Structural stability on hyperbolic sets

We conclude the chapter by a sketch of the famous structural stability theorem of

D. Anosov, using the shadowing lemma.

Lemma III.22. Let ƒ be a hyperbolic set of the diffeomorphism ' and assume

to be another diffeomorphism leaving ƒ invariant, .ƒ/ D ƒ, and being near '

in the sense of

j'  j

<":

Then, for " small enough, ƒ is also a hyperbolic set of .

Proof. Exercise. Hint: To ﬁnd the hyperbolic splitting of the tangent space in

2 ƒ consider the orbit of ,

/; j 2 Z;

which is an "-pseudo orbit on ƒ for the diffeomorphism ', since

d.q

j C1

;'.q

// D d. .q

/; '.q

// j  'j

<"; j 2 Z:

Using the assumption jd'.q

/d .q

/j <", the existence of the invariant splitting

follows by means of the arguments in the proof of the shadowing lemma. 

Theorem III.23 (Structural stability 'j

). Let ƒ be a hyperbolic set of the diffeo-

morphism ' and let be another diffeomorphism satisfying .ƒ/ D ƒ. Then,

there exists for every ı>0an ">0having the following property. If

j'  j

<";

then there exists a homeomorphism hW ƒ ! ƒ satisfying

D h

1

B ' B h

and jh  Idj

Cjh

1

 Idj

 2ı. Moreover, if ı>0is small enough, there

exists a unique homeomorphism h having these properties.

Proof [Shadowing lemma]. (1) Deﬁnition of the homeomorphism h. In view of

the remark in the shadowing lemma, we ﬁnd for every ı<ı

two constants "

.ı/>0and  D .ı/>0such that for every diffeomorphism satisfying

j'  j

  and for every "

-pseudo orbit q D .q

j 2Z

of ' there exists a

III.7. Structural stability on hyperbolic sets 125

unique ı-shadowing orbit for the diffeomorphism . Setting " D minf"

;g we

deﬁne for satisfying j'  j

<"the map hW ƒ ! ƒ in the following way.

Consider the point q

2 ƒ and let q

/ for j 2 Z be the orbit of q

under

the map . Due to

d.q

j C1

;'.q

// D d. .q

/; '.q

// j'  j

<";

the sequence q D .q

/ is an "-pseudo orbit for the diffeomorphism '.Ifp D .p

is the corresponding unique ı-shadowing orbit of q for the diffeomorphism ',we

deﬁne

h.q

/ D p

This map h satisﬁes the estimate d.q; h.q//  ı for all q in ƒ.

(2) Continuity of h. In order to prove the continuity of the map h we take a

sequence x

2 ƒ satisfying x

! x. Since ƒ is compact, the sequence y

h.x

/ has a convergent subsequence in ƒ. Denoting by y its limit, we claim that

y D h.x/. In view of the deﬁnition of h,

d.'

//  ı

for every m  0 and consequently,

d.'

.y/;

.x//  ı  ı

;j2 Z:

Therefore, the orbit .'

.y//

j 2Z

is a ı

-shadowing orbit of the sequence .

.x//

j 2Z

on ƒ. In view of the deﬁnition of the map h, the orbit .'

.h.x///

j 2Z

is another

-shadowing orbit (even ı-shadowing) of the same sequence. From the uniqueness

of the shadowing orbit, we conclude '

.h.x// D '

.y/ and hence h.x/ D y,as

claimed.

(3) h is a homeomorphism. According to Lemma III.22 we can exchange the

roles of and '. By the same construction we obtain a continuous mapping h

and

conclude from the uniqueness statement in the shadowing lemma that h

D h

1

(4) Conjugation and estimate. In view of the construction,

1

B ' B h.q

/ D h

1

B '.p

/ D h

1

/ D q

D .q

hence h is the desired conjugation.

(5) Uniqueness. Let ı>0be so small that the uniqueness in the shadowing

lemma holds true and assume that the homeomorphism h satisﬁes the estimate

jh  Idj

<ı, where h is a conjugation, so that

.x// D '

.h.x//

for all x 2 ƒ and j 2 Z. Due to d.h.

.x//;

.x// jh Idj

<ı, the orbit

.h.x// D h.

.x// is therefore the unique ı-shadowing orbit of the sequence

.x/. In particular, the initial point h.x/ of the orbit is uniquely determined by the

point x. Hence, the homeomorphism h is unique and the proof of Theorem III.23

is complete. 

126 Chapter III. Hyperbolic sets

Corollary III.24. An Anosov diffeomorphism of a compact manifold is structurally

stable. In particular, every hyperbolic torus automorphism is structurally stable.

We would like to add that in case the hyperbolic set is a compact Riemannian

manifold, J. Moser gave in [71] a direct analytical proof of the structural stability

theorem of D. Anosov avoiding the shadowing lemma. The proof is also presented

in the book by W. Szlenk [113].

Literature. The proof of Smale’s theorem about embeddings of Bernoulli systems

is due to K. Palmer in [80]. Useful references about hyperbolicity theory are the

monograph [49] by B. Hasselblatt and A. Katok, the monograph [85]byS.Y.Pi-

lyugin, the survey articles [48] by B. Hasselblatt and [83] by Y. Pesin. An efﬁcient

introduction to hyperbolic dynamics are the lectures [119] by J.-C.Yoccoz. Classics

are A. Katok’s article [58] and D. Anosov’s work [7]. The partial hyperbolicity is

treated in the lectures [84] by Y. Pesin.

Chapter IV

Gradientlike ﬂows

So far we have dealt with discrete dynamical systems whose dynamics is determined

by iterations of mappings. We now consider systems whose dynamics are described

by ﬂows generated by smooth vector ﬁelds and start the chapter by recalling some

facts about ordinary differential equations. In order to describe the asymptotic

behavior of orbits of ﬂows, the concepts of limit sets and attractors are introduced.

In the exampleof the gradient ﬂow on a compact manifold, everyorbit approaches, in

forward and in backward time, the set of equilibrium points. Here all the movements

slow down and come to a halt at the equilibrium points. Equilibrium points are found

by mini-max principles based on indexfunctions such as the Lusternik–Schnirelman

category. There is an intimate and fruitful relation between the dynamics of gradient

ﬂows on compact manifolds and the topology of the underlying manifold, described

by the Morse inequalities presented at the end of the chapter. The Morse theory

will only be sketched.

IV.1 Flow of a vector ﬁeld, recollections from ODE

In order to recall the concept of the ﬂow of a vector ﬁeld, we consider the open set

  R

and the vector ﬁeld X W  ! R

of class C

for r  1. The vector ﬁeld

X is, in particular, locally Lipschitz-continuous.

If x



2 , then there exists an open ball B



/   around x



of radius

a>0, an open interval I D ."; "/ around 0 and a C

map

' W I  B



/ !   R

;.t;x/7! '.t; x/ D '

.x/;

such that for every x 2 B



/ the curve t 7! '

.x/, t 2 I is the unique solution

of the Cauchy initial value problem

.x/ D X.'

.x//; t 2 R;

.x/ D x:

The map ' is called the local ﬂow of X. For the existence, uniqueness and regularity

of the ﬂow, we refer to the book [5, Chapter II] by H. Amann. In view of its unique-

ness, every solution '

.x/ with the initial condition '

.x/ D x can be continued

onto the maximal interval



 t



.x/; t

.x/



 R

where the upper bound of the interval (or the exit time of the solution) is deﬁned by

.x/ ´ sup

  0 jPx D X.x/; x.0/ D x has a solution on Œ0; 



128 Chapter IV. Gradientlike ﬂows

and analogously the lower bound (respectively the entrance time) t



.x/ is deﬁned.

We point out that, in case the vector ﬁeld is not linear, the maximal existence

interval I

is not necessarily the real line R, as the following example shows.

Example. Let  D R and X.x/ D x

. Then the ﬂow of the Cauchy initial value

problem

Px D x

;

x.0/ D x

is equal to '

.x/ D

1tx

and so the maximal existence intervals are the intervals

D .1;

/; x > 0;

D R;xD 0;

D .

; 1/; x < 0:

It follows from the uniqueness of the solution of the Cauchy initial values prob-

lem that the ﬂow of a time independent vector ﬁeld satisﬁes

.x// D '

tCs

.x/ D '

.x//

on the domains of deﬁnition. Indeed, the two curves t 7! '

.x// and t 7!

tCs

.x/ solve the same Cauchy initial value problem with the same initial condition

x.0/ D '

.x/ at the time t D 0.

In the special case of  D R

and I

D R for all x 2 R

the ﬂow deﬁnes a

one-parameter group of diffeomorphisms f'

j t 2 Rg,

W R

! R

;x7! '

.x/

satisfying, for all t;s 2 R,

.x// D '

tCs

.x/ D '

.x//; .'

1

D '

1

D Id :

If   R

is an open subset, the ﬂow deﬁnes local groups '

of diffeomorphisms

on their domains of deﬁnition. A ﬂow is called a global ﬂow (or a complete ﬂow),

if it is deﬁned on R  . Next, we describe conditions which guarantee that the

ﬂow is complete. We ﬁrst remark that if a solution does not exist for all times, then

it must leave every compact set in positive or in negative time.

Proposition IV.1. We assume that X W  ! R

is a C

vector ﬁeld and that the

point x 2  satisﬁes t

.x/ < 1. Then, there exists for every compact set K

containing x 2 K   a time 

.x/ such that

.x/ … K; 

<t<t

.x/:

Hence, if the solution '

.x/ remains in a compact set K   for all 0  t<

.x/, then t

.x/ D1.

An analogous result holds true for t



.x/.

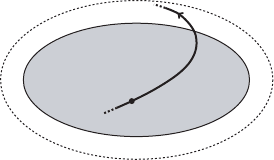
IV.1. Flow of a vector ﬁeld, recollections from ODE 129



x.0/

x.t/

Figure IV.1. If t

.x/ < 1, then the solution x.t/ D '

.x/ leaves every compact set K.

Proof [Local ﬂow]. Arguing by contradiction we assume the existence of a com-

pact set K containing x 2 K   and the existence of a sequence t

% t

.x/ < 1

satisfying

´ '

.x/ 2 K; n  1:

Since K is compact, we ﬁnd a convergent subsequence

D '

! x



2 K:

In view of the existence of the local ﬂow, we ﬁnd a ball B



/   and an interval

I D ."; "/ such that the solution '

./ exists for every  2 B



/ and every

t 2 I .Forn large we conclude from the uniqueness of the ﬂow that

/ D '

.x// D '

tCt

.x/; t 2 I;

so that the solution exists for all 0  t<t

C ". However, if n is large, then

" C t

.x/, contradicting the deﬁnition of t

.x/ and completing the proof.



Proposition IV.2. Let X W R

! R

be a bounded C

vector ﬁeld, satisfying

sup

x2R

jX.x/jμM<1:

Then, I

D R for all x 2 R

Proof. Arguing again by contradiction, we ﬁnd a point x

satisfying I

¤ R and

we assume that t

/<1. The local ﬂow satisﬁes

/  x

X.'

// ds;

so that

/  x

j

jX.'

//jds  tM  t

/M < 1

130 Chapter IV. Gradientlike ﬂows

for all 0  t<t

/. Consequently, the solution remains in the compact set

/, where R D t

/M , in contradiction to Proposition IV.1. An analogous

argument applies in case t



/ is ﬁnite. 

More generally, the ﬂow of a linearly bounded vector ﬁeld is complete.

Proposition IV.3. Let X W R

! R

be a linear bounded C

vector ﬁeld, hence

satisfying

jX.x/ja C bjxj;x2 R

with non-negative constants a; b 2 R. Then, I

D R for all x 2 R

Proof. Assume that t

/<1 and consider the time interval 0  t<t

From

/  x

X.'

// ds

we deduce the estimate

/ja.t/ C b

/jds

for all 0  t<t

/, where a.t/ ´jx

jCat.

According to the Lemma of Gronwall below, the solution '

/ is therefore

bounded, in contradiction to Proposition IV.1. Analogous arguments lead to a con-

tradiction under the assumption that t



/ is ﬁnite, and the proof of the proposition

is ﬁnished. 

The Lemma of Gronwall is a useful tool to obtain estimates in ordinary differ-

ential equations. We only need a special case and refer to Chapter II in the book

[5] by H. Amann for more general versions.

Lemma IV.4 (Gronwall). We consider an interval I  R, a point t

2 I and non-

negative functions u; a; b W I ! R and we assume that the function a is increasing.

u.t/  a.t/ C

b.s/u.s/ ds

for all t 2 I;

then

u.t/  a.t/e

b.s/dsj

for all t 2 I:

Proof. We carry out the proof for t

D 0 and t  0. Introducing the functions

v.t/ ´

b.s/u.s/ ds;

.t/ ´ e



b.s/ds

;