Zee A. Quantum Field Theory in a Nutshell

Подождите немного. Документ загружается.

272 | IV. Symmetry and Symmetry Breaking

Before we blindly calculate, however, let us ask ourselves how sad we would be if either of

the two currents J

and J

fails to be conserved. Well, we would be very upset if the vector

current is not conserved. The corresponding charge Q =



counts the number of

fermions. We wouldn’t want our fermions to disappear into thin air or pop out of nowhere.

Furthermore, it may please us to couple the photon to the fermion field ψ . In that case,

you would recall from chapter II.7 that we need ∂

= 0 to prove gauge invariance and

hence show that the photon has only two degrees of polarization. More explicitly, imagine

a photon line coming into the vertex labeled by μ in figure IV.7.1a and b with propagator

(i/k

)[ξ(k

1μ

1ρ

) − g

μρ

]. The gauge dependent term ξ(k

1μ

1ρ

) would not go away if

the vector current is not conserved, that is, if k

1μ



λμν

fails to vanish.

On the other hand, quite frankly, just between us friends, we won’t get too upset if

quantum fluctuation violates axial current conservation. Who cares if the axial charge



is not constant in time?

Shifting integration variable

So, do k

1μ



λμν

and k

2ν



λμν

vanish? We will look over Professor Confusio’s shoulders as

he calculates k

1μ



λμν

. (We are now in the 1960s, long after the development of renor-

malization theory as described in chapter III.1 and Confusio has managed to get a tenure

track assistant professorship.) He hits 

λμν

as written in (1) with k

1μ

and using what he

learned in chapter II.7 writes k

in the first term as p − ( p − k

) and in the second term

as ( p − k

) − ( p − q), thus obtaining

1μ



λμν

, k

)

= i



(2π)

tr(γ

p − q

p − k

− γ

p − k

p

) (2)

Just as in chapter II.7, Confusio recognizes that in the integrand the first term is just the

second term with the shift of the integration variable p → p − k

. The two terms cancel

and Professor Confusio publishes a paper saying k

1μ



λμν

= 0, as we all expect.

Remember back in chapter II.7 I said we were going to worry later about whether it is

legitimate to shift integration variables. Now is the time to worry!

You could have asked your calculus teacher long ago when it is legitimate to shift

integration variables. When is



+∞

−∞

dpf (p + a) equal to



+∞

−∞

dpf (p)? The difference

between these two integrals is



+∞

−∞

dp(a

f(p)+

...

) = a(f (+∞) − f(−∞)) +

...

Clearly, if f(+∞) and f(−∞) are two different constants, then it is not okay to shift. But

if the integral



+∞

−∞

dpf (p) is convergent, or even logarithmically divergent, it is certainly

okay. It was okay in chapter II.7 but definitely not here in (2)!

IV.7. Chiral Anomaly | 273

As usual, we rotate the Feynman integrand to Euclidean space. Generalizing our obser-

vation above to d-dimensional Euclidean space, we have



p[f(p+ a) −f(p)] =



p[a

∂

f(p)+

...

]

which by Gauss’s theorem is given by a surface integral over an infinitely large sphere

enclosing all of Euclidean spacetime and hence equal to

lim

P →∞





f(P)S

d−1

(P )

where S

d−1

(P ) is the area of a (d −1)-dimensional sphere (see appendix D) and where an

average over the surface of the sphere is understood. (Recall from our experience evaluating

Feynman diagrams that the average of P

is equal to

μν

by a symmetry argument,

with the normalization

fixed by contracting with η

μν

.) Rotating back, we have for a 4-

dimensional Minkowskian integral



p[f(p+ a) −f(p)] = lim

P →∞





f(P)(2π

) (3)

Note the i from Wick rotating back.

Applying (3) with

f(p)= tr



p − k

p



tr[γ

( p − k

)γ

pγ

]

(p − k

)

4iε

τνσλ

2τ

(p − k

)

we obtain

1μ



λμν

(2π)

lim

P →∞

i(−k

)

4iε

τνσλ

2τ

2π

8π

λντ σ

1τ

2σ

Contrary to what Confusio said, k

1μ



λμν

= 0.

As I have already said, this would be a disaster. Fermion number is not conserved and

matter would be disintegrating all around us! What is the way out?

In fact, we are only marginally smarter than Professor Confusio. We did not notice that

the integral defining 

λμν

in (1) is linearly divergent and is thus not well defined.

Oops, even before we worry about calculating k

1μ



λμν

and k

2ν



λμν

we better worry

about whether or not 

λμν

depends on the physicist doing the calculation. In other

words, suppose another physicist chooses

to shift the integration variable p in the linearly

divergent integral in (1) by an arbitrary 4-vector a and define



λμν

(a, k

, k

)

= (−1)i



(2π)

tr(γ

p + a − q

p + a − k

p + a

)

+{μ, k

↔ ν, k

} (4)

There can be as many results for the Feynman diagrams in figure IV.7.1a and b as there

are physicists! That would be the end of physics, or at least quantum field theory, for sure.

This is the freedom of choice in labeling internal momenta mentioned in chapter I.7.

274 | IV. Symmetry and Symmetry Breaking

Well, whose result should we declare to be correct?

The only sensible answer is that we trust the person who chooses an a such that

1μ



λμν

(a, k

, k

) and k

2ν



λμν

(a, k

, k

) vanish, so that the photon will have the right

number of degrees of freedom should we introduce a photon into the theory.

Let us compute 

λμν

(a, k

, k

) − 

λμν

, k

) by applying (3) to f(p) =

tr(γ

p−q

p−k

p

). Noting that

f(P)= lim

P →∞

tr(γ

Pγ

P)

tr(γ

Pγ

P)− P

tr(γ

Pγ

)

+4iP

σνμλ

we see that



λμν

(a, k

, k

) − 

λμν

, k

) =

8π

lim

P →∞

σνμλ

+{μ, k

↔ ν, k

}

8π

σνμλ

+{μ, k

↔ ν, k

} (5)

There are two independent momenta k

and k

in the problem, so we can take a =

α(k

+ k

) + β(k

− k

). Plugging into (5), we obtain



λμν

(a, k

, k

) = 

λμν

, k

) +

iβ

4π

λμνσ

− k

)

(6)

Note that α drops out.

As expected, 

λμν

(a, k

, k

) depends on β , and hence on a. Our unshakable desire to

have a conserved vector current, that is, k

1μ



λμν

(a, k

, k

) = 0, now fixes the parameter β

upon recalling

1μ



λμν

, k

) =

8π

λντ σ

1τ

2σ

Hence, we must choose to deal with 

λμν

(a, k

, k

) with β =−

One way of viewing all this is to say that the Feynman rules do not suffice in determining

0|TJ

(0)J

) |0. They have to be supplemented by vector current conservation.

The amplitude 0|TJ

(0)J

) |0 is defined by 

λμν

(a, k

, k

) with β =−

Quantum fluctuation violates axial current conservation

Now we come to the punchline of the story. We insisted that the vector current be conserved.

Is the axial current also conserved?

To answer this question, we merely have to compute



λμν

(a, k

, k

) = q



λμν

, k

) +

4π

μνλσ

1λ

2σ

(7)

IV.7. Chiral Anomaly | 275

By now, you know how to do this:



λμν

, k

) = i



(2π)



p − q

p − k

−γ

p − k

p



+{μ, k

↔ ν, k

}

4π

μνλσ

1λ

2σ

(8)

Indeed, you recognize that the integration has already been done in (2). We finally obtain



λμν

(a, k

, k

) =

2π

μνλσ

1λ

2σ

(9)

The axial current is not conserved!

In summary, in the simple theory L =

ψiγ

∂

ψ while the vector and axial currents are

both conserved classically, quantum fluctuation destroys axial current conservation. This

phenomenon is known variously as the anomaly, the axial anomaly, or the chiral anomaly.

Consequences of the anomaly

As I said, the anomaly is an extraordinarily rich subject. I will content myself with a series

of remarks, the details of which you should work out as exercises.

1. Suppose we gauge our simple theory L =

ψiγ

(∂

−ieA

)ψ and speak of A

as the photon

field. Then in figure IV.7.1 we can think of two photon lines coming out of the vertices labeled

μ and ν. Our central result (9) can then be written elegantly as two operator equations:

Classical physics: ∂

= 0 (10)

Quantum physics: ∂

(4π)

μνλσ

μν

λσ

(11)

The divergence of the axial current ∂

is not zero, but is an operator capable of producing

two photons.

2. Applying the same type of argument as in chapter IV.2 we can calculate the rate of the

decay π

→γ +γ . Indeed, historically people used the erroneous result (10) to deduce that

this experimentally observed decay cannot occur! See exercise IV.7.2. The resolution of this

apparent paradox led to the correct result (11).

3. Writing the Lagrangian in terms of left and right handed fields ψ

and ψ

and introducing

the left and right handed currents J

≡

and J

≡

, we can repackage the

anomaly as

∂

(4π)

μνλσ

μν

λσ

and

∂

=−

(4π)

μνλσ

μν

λσ

(12)

276 | IV. Symmetry and Symmetry Breaking

(Hence the name chiral!) We can think of left handed and right handed fermions running

around the loop in figure IV.7.1, contributing oppositely to the anomaly.

4. Consider the theory L =

ψ(iγ

∂

−m)ψ . Then invariance under the transformation ψ →

iθγ

ψ is spoiled by the mass term. Classically, ∂

= 2m

ψiγ

ψ: The axial current is

explicitly not conserved. The anomaly now says that quantum fluctuation produces an

additional term. In the theory L =

ψ[iγ

(∂

− ieA

) − m]ψ, we have

∂

= 2m

ψiγ

ψ +

(4π)

μνλσ

μν

λσ

(13)

5. Recall that in chapter III.7 we introduced Pauli-Villars regulators to calculate vacuum

polarization. We subtract from the integrand what the integrand would have been if the

electron mass were replaced by some regulator mass. The analog of electron mass in (1) is

in fact 0 and so we subtract from the integrand what the integrand would have been if 0

were replaced by a regulator mass M . In other words, we now define



λμν

, k

) = (−1)i



(2π)



p − q

p − k

p

−γ

p − q −M

p − k

− M

p − M



+{μ, k

↔ ν, k

}. (14)

Note that as p →∞the integrand now vanishes faster than 1/p

. This is in accordance

with the philosophy of regularization outlined in chapters III.1 and III.7: For p  M , the

threshold of ignorance, the integrand is unchanged. But for p  M , the integrand is cut

off. Now the integral in (14) is superficially logarithmically divergent and we can shift the

integration variable p at will.

So how does the chiral anomaly arise? By including the regulator mass M we have broken

axial current conservation explicitly. The anomaly is the statement that this breaking persists

even when we let M tend to infinity. It is extremely instructive (see exercise IV.7.4) to work

this out.

6. Consider the nonabelian theory L =

ψiγ

(∂

− igA

)ψ . We merely have to include in

the Feynman amplitude a factor of T

at the vertex labeled by μ and a factor of T

at the vertex

labeled by ν . Everything goes through as before except that in summing over all the different

fermions that run around the loop we obtain a factor tr T

. Thus, we see instantly that

in a nonabelian gauge theory

∂

(4π)

μνλσ

tr F

μν

λσ

(15)

where F

μν

= F

μν

is the matrix field strength defined in chapter IV.5. Nonabelian sym-

metry tells us something remarkable: The object ε

μνλσ

tr F

μν

λσ

contains not only a term

quadratic in A, but also terms cubic and quartic in A, and hence there is also a chiral

anomaly with three and four gauge bosons coming in, as indicated in figure IV.7.2a and

b. Some people refer to the anomaly produced in figures IV.7.1 and IV.7.2 as the triangle,

square, and pentagon anomaly. Historically, after the triangle anomaly was discovered, there

was a controversy as to whether the square and pentagon anomaly existed. The nonabelian

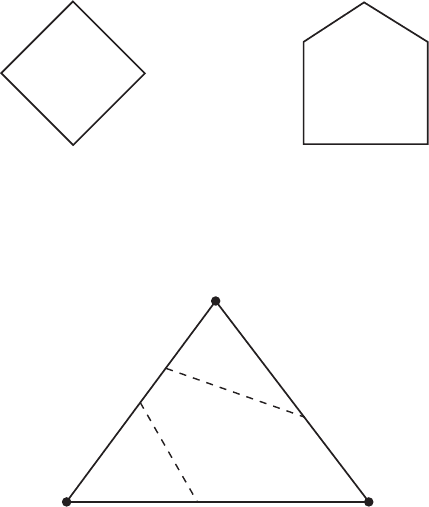
IV.7. Chiral Anomaly | 277

(a)

(b)

Figure IV.7.2

Figure IV.7.3

symmetry argument given here makes things totally obvious, but at the time people calcu-

lated Feynman diagrams explicitly and, as we just saw, there are subtleties lying in wait for

the unwary.

7. We will see in chapter V.7 that the anomaly has deep connections to topology.

8. We computed the chiral anomaly in the free theory L =

ψ(iγ

∂

− m)ψ . Suppose we

couple the fermion to a scalar field by adding fϕ

ψψ or to the electromagnetic field for

that matter. Now we have to calculate higher order diagrams such as the three-loop diagram

in figure IV.7.3. You would expect that the right-hand side of (9) would be multiplied by

1 + h(f , e,

...

), where h is some unknown function of all the couplings in the theory.

Surprise! Adler and Bardeen proved that h = 0. This apparently miraculous fact, known as

the nonrenormalization of the anomaly, can be understood heuristically as follows. Before

we integrate over the momenta of the scalar propagators in figure IV.7.3 (labeled by w

and w

) the Feynman integrand has seven fermion propagators and thus is more than

sufficiently convergent that we can shift integration variables with impunity. Thus, before

we integrate over w

and w

all the appropriate Ward identities are satisfied, for instance,



λμν

3 loops

, k

; w

, w

) =0. You can easily complete the proof. You will give a proof

based

on topology in exercise V.7.13.

For a simple proof not involving topology, see J. Collins, Renormalization, p. 352.

278 | IV. Symmetry and Symmetry Breaking

(a)

π°

γγ

(b)

π°

Figure IV.7.4

9. The preceding point was of great importance in the history of particle physics as it led directly

to the notion of color, as we will discuss in chapter VII.3. The nonrenormalization of the

anomaly allowed the decay amplitude for π

→γ + γ to be calculated with confidence in the

late 1960s. In the quark model of the time, the amplitude is given by an infinite number of

Feynman diagrams, as indicated in figure IV.7.4 (with a quark running around the fermion

loop), but the nonrenormalization of the anomaly tells us that only figure IV.7.4a contributes.

In other words, the amplitude does not depend on the details of the strong interaction. That

it came out a factor of 3 too small suggested that quarks come in 3 copies, as we will see in

chapter VII.3.

10. It is natural to speculate as to whether quarks and leptons are composites of yet more

fundamental fermions known as preons. The nonrenormalization of the chiral anomaly

provides a powerful tool for this sort of theoretical speculation. No matter how complicated

the relevant interactions might be, as long as they are described by field theory as we know

it, the anomaly at the preon level must be the same as the anomaly at the quark-lepton level.

This so-called anomaly matching condition

severely constrains the possible preon theories.

11. Historically, field theorists were deeply suspicious of the path integral, preferring the

canonical approach. When the chiral anomaly was discovered, some people even argued that

the existence of the anomaly proved that the path integral was wrong. Look, these people

said, the path integral



ψDψ e



ψiγ

(∂

−iA

)ψ

(16)

is too stupid to tell us that it is not invariant under the chiral transformation ψ →e

iθγ

ψ .

Fujikawa resolved the controversy by showing that the path integral did know about the

anomaly: Under the chiral transformation the measure D

ψDψ changes by a Jacobian.

Recall that this was how I motivated this chapter: The action may be invariant but not the

path integral.

G. ’t Hooft, in: G. ’t Hooft et al., eds., Recent Developments in Gauge Theories; A. Zee, Phys. Lett. 95B:290, 1980.

IV.7. Chiral Anomaly | 279

Exercises

IV.7.1 Derive (11) from (9). The momentum factors k

1λ

and k

2σ

in (9) become the two derivatives in F

μν

λσ

(11).

IV.7.2 Following the reasoning in chapter IV.2 and using the erroneous (10) show that the decay amplitude for

the decay π

→ γ + γ would vanish in the ideal world in which the π

is massless. Since the π

does

decay and since our world is close to the ideal world, this provided the first indication historically that

(10) cannot possibly be valid.

IV.7.3 Repeat all the calculations in the text for the theory L =

ψ(iγ

∂

− m)ψ .

IV.7.4 Take the Pauli-Villars regulated 

λμν

, k

) and contract it with q

. The analog of the trick in chapter II.7

is to write qγ

in the second term as [2M + ( p − M) − ( p − q +M)]γ

. Now you can freely shift

integration variables. Show that



λμν

, k

) =−2M

μν

, k

) (17)

where



μν

, k

) ≡ (−1)i



(2π)



p − q −M

p − k

− M

p − M



+{μ, k

↔ ν, k

}

Evaluate 

μν

and show that 

μν

goes as 1/M in the limit M →∞and so the right hand side of (17)

goes to a finite limit. The anomaly is what the regulator leaves behind as it disappears from the low

energy spectrum: It is like the smile of the Cheshire cat. [We can actually argue that 

μν

goes as 1/M

without doing a detailed calculation. By Lorentz invariance and because of the presence of γ

, 

μν

must be proportional to ε

μνλρ

1λ

2ρ

, but by dimensional analysis, 

μν

must be some constant times

μνλρ

1λ

2ρ

/M. You might ask why we can’t use something like 1/(k

)

instead of 1/M to make the

dimension come out right. The answer is that from your experience in evaluating Feynman diagrams in

(3 + 1)-dimensional spacetime you can never get a factor like 1/(k

)

IV.7.5 There are literally N ways of deriving the anomaly. Here is another. Evaluate



λμν

, k

) = (−1)i



(2π)



p − q −m

p − k

− m

p − m



+{μ, k

↔ ν, k

}

in the massive fermion case not by brute force but by first using Lorentz invariance to write



λμν

, k

) = ε

λμνσ

1σ

...

+ ε

μνσ τ

1σ

2τ

where A

≡ A

, k

, q

) are eight functions of the three Lorentz scalars in the problem. You are

supposed to fill in the dots. By counting powers as in chapters III.3 and III.7 show that two of these

functions are given by superficially logarithmically divergent integrals while the other six are given by

perfectly convergent integrals. Next, impose Bose statistics and vector current conservation k

1μ



λμν

0 = k

2ν



λμν

to show that we can avoid calculating the superficially logarithmically divergent integrals.

Compute the convergent integrals and then evaluate q



λμν

, k

IV.7.6 Discuss the anomaly by studying the amplitude

0|TJ

(0)J

) |0

280 | IV. Symmetry and Symmetry Breaking

given in lowest orders by triangle diagrams with axial currents at each vertex. [Hint: Call the momentum

space amplitude 

λμν

, k

).] Show by using (γ

)

= 1 and Bose symmetry that



λμν

, k

) =

[

λμν

(a, k

, k

) + 

μνλ

(a, k

, −q) + 

νλμ

(a, −q , k

)]

Now use (9) to evaluate q



λμν

, k

IV.7.7 Define the fermionic measure Dψ in (16) carefully by going to Euclidean space. Calculate the Jacobian

upon a chiral transformation and derive the anomaly. [Hint: For help, see K. Fujikawa, Phys. Rev. Lett.

42: 1195, 1979.]

IV.7.8 Compute the pentagon anomaly by Feynman diagrams in order to check remark 6 in the text. In other

words, determine the coefficient c in ∂

...

+ cε

μνλσ

tr A

Part V Field Theory and Collective Phenomena

I mentioned in the introduction that one of the more intellectually satisfying developments

in the last two or three decades has been the increasingly important role played by field

theoretic methods in condensed matter physics. This is a rich and diverse subject; in this

and subsequent chapters I can barely describe the tip of the iceberg and will have to content

myself with a few selected topics.

Historically, field theory was introduced into condensed matter physics in a rather direct

and straightforward fashion. The nonrelativistic electrons in a condensed matter system

can be described by a field ψ , along the lines discussed in chapter III.5. Field theoretic

Lagrangians may then be written down, Feynman diagrams and rules developed, and so

on and so forth. This is done in a number of specialized texts. What we present here is to a

large extent the more modern view of an effective field theoretic description of a condensed

matter system, valid at low energy and momentum. One of the fascinations of condensed

matter physics is that due to highly nontrivial many body effects the low energy degrees

of freedom might be totally different from the electrons we started out with. A particularly

striking example (to be discussed in chapter VI.2) is the quantum Hall system, in which

the low energy effective degree of freedom carries fractional charge and statistics.

Another advantage of devoting a considerable portion of a field theory book to condensed

matter physics is that historically and pedagogically it is much easier to understand the

renormalization group in condensed matter physics than in particle physics.

I will defiantly not stick to a legalistic separation between condensed matter and particle

physics. Some of the topics treated in Parts V and VI actually belong to particle physics.

And of course I cannot be responsible for explaining condensed matter physics, any more

than I could be responsible for explaining particle physics in chapter IV.2.