Zee A. Quantum Field Theory in a Nutshell

Подождите немного. Документ загружается.

252 | IV. Symmetry and Symmetry Breaking

but





d x =



S is precisely the flux enclosed by the closed curve (P

−P

), namely

the curve going from a to b along P

and then returning from b to a along (−P

) since

complex conjugation in effect reverses the direction of the path P

. Remarkably, the

electron feels the effect of the magnetic field even though it never wanders into a region

with a magnetic field present.

When the Aharonov-Bohm paper was first published, no less an authority than Niels

Bohr was deeply disturbed. The effect has since been conclusively demonstrated in a series

of beautiful experiments by Tonomura and collaborators.

Coleman once told of a gedanken prank that connects the Aharonov-Bohm effect to

Dirac quantization of magnetic charge. Let us fabricate an extremely thin solenoid so that

it is essentially invisible and thread it into the lab of an unsuspecting experimentalist,

perhaps our friend from chapter III.1. We turn on a current and generate a magnetic field

through the solenoid. When the experimentalist suddenly sees the magnetic flux coming

out of apparently nowhere, she gets so excited that she starts planning to go to Stockholm.

What is the condition that prevents the experimentalist from discovering the prank? A

careful experimentalist might start scattering electrons around to see if she can detect a

solenoid. The condition that she does not see an Aharonov-Bohm effect and thus does

not discover the prank is precisely that the flux going through the solenoid is an integer

times 2π/e. This implies that the apparent magnetic monopole has precisely the magnetic

charge predicted by Dirac!

Exercises

IV.4.1 Prove dd = 0.

IV.4.2 Show by writing out the components explicitly that dF = 0 expresses something that you are familiar

with but disguised in a compact notation.

IV.4.3 Consider F = (g/4π) d cos θdϕ. By transforming to Cartesian coordinates show that this describes a

magnetic field pointing outward along the radial direction.

IV.4.4 Restore the factors of  and c in Dirac’s quantization condition.

IV.4.5 Write down the reparametrization-invariant current J

μνλ

of a membrane.

IV.4.6 Let g(x) be the element of a group G. The 1-form v = gdg

†

is known as the Cartan-Maurer form.

Then tr v

is trivially closed on an N -dimensional manifold since it is already an N-form. Consider

Q =



tr v

with S

the N-dimensional sphere. Discuss the topological meaning of Q. These con-

siderations will become important later when we discuss topology in field theory in chapter V.7. [Hint:

Study the case N = 3 and G = SU(2).]

IV.5 Nonabelian Gauge Theory

Most such ideas are eventually discarded or shelved. But some

persist and may become obsessions. Occasionally an obsession

does finally turn out to be something good.

—C. N. Yang talking about an idea that he first had as a

student and that he kept coming back to year after year.

Local transformation

It was quite a nice little idea.

To explain the idea Yang was talking about, recall our discussion of symmetry in

chapter I.10. For the sake of definiteness let ϕ(x) ={ϕ

(x), ϕ

(x),

...

, ϕ

(x)} be an N-

component complex scalar field transforming as ϕ(x) → U ϕ(x), with U an element of

SU (N). Since ϕ

†

→ ϕ

†

and U

†

U = 1, we have ϕ

†

ϕ → ϕ

†

ϕ and ∂ϕ

†

∂ϕ → ∂ϕ

†

∂ϕ. The

invariance of the Lagrangian L =∂ϕ

†

∂ϕ − V(ϕ

†

ϕ) under SU (N) is obvious for any poly-

nomial V .

In the theoretical physics community there are many more people who can answer well-

posed questions than there are people who can pose the truly important questions. The

latter type of physicist can invariably also do much of what the former type can do, but the

reverse is certainly not true.

In 1954 C.N. Yang and R. Mills asked what will happen if the transformation varies from

place to place in spacetime, or in other words, if U = U(x) is a function of x .

Clearly, ϕ

†

ϕ is still invariant. But in contrast ∂ϕ

†

∂ϕ is no longer invariant. Indeed,

∂

ϕ → ∂

(Uϕ) = U∂

ϕ + (∂

U)ϕ =U[∂

ϕ + (U

†

∂

U)ϕ]

To cancel the unwanted term (U

†

∂

U)ϕ, we generalize the ordinary derivative ∂

to a

covariant derivative D

, which when acting on ϕ, gives

ϕ(x) = ∂

ϕ(x) − iA

(x)ϕ(x) (1)

The field A

is called a gauge potential in direct analogy with electromagnetism.

C. N. Yang, Selected Papers 1945–1980 with Commentary,p.19.

254 | IV. Symmetry and Symmetry Breaking

How must A

transform, so that D

ϕ(x) → U(x)D

ϕ(x)? In other words, we would

like D

ϕ(x) to transform the way ∂

ϕ(x) transformed when U did not depend on x.If

so, then [D

ϕ(x)]

†

ϕ(x) → [D

ϕ(x)]

†

ϕ(x) and can be used as an invariant kinetic

energy term for the field ϕ.

Working backward, we see that D

ϕ(x) → U(x)D

ϕ(x) if ( and it goes without saying

that you should be checking this)

→ UA

†

− i(∂

U)U

†

= UA

†

+ iU∂

†

(2)

(The equality follows from UU

†

= 1.) We refer to A

as the nonabelian gauge potential

and to (2) as a nonabelian gauge transformation.

Let us now make a series of simple observations.

1. Clearly, A

have to be N by N matrices. Work out the transformation law for A

†

using

(2) and show that the condition A

− A

†

= 0 is preserved by the gauge transformation.

Thus, it is consistent to take A

to be hermitean. Specifically, you should work out what

this means for the group SU(2) so that U = e

iθ

τ/2

where θ

τ = θ

, with τ

the familiar

Pauli matrices.

2. Writing U = e

iθ

with T

the generators of SU (N ), we have

→ A

+ iθ

, A

] +∂

(3)

under an infinitesimal transformation U 1 + iθ

T . For most purposes, the infinitesimal

form (3) suffices.

3. Taking the trace of (3) we see that the trace of A

does not transform and so we can take A

to be traceless as well as hermitean. This means that we can always write A

= A

and

thus decompose the matrix field A

into component fields A

. There are as many A

’s as

there are generators in the group [3 for SU(2), 8 for SU(3), and so forth.]

4. You are reminded in appendix B that the Lie algebra of the group is defined by [T

, T

] =

abc

, where the numbers f

abc

are called structure constants. For example, f

abc

= ε

abc

for SU(2). Thus, (3) can be written as

→ A

− f

abc

+ ∂

(4)

Note that if θ does not depend on x , the A

’s transform as the adjoint representation of the

group.

5. If U(x) =e

iθ (x)

is just an element of the abelian group U(1), all these expressions simplify

and A

is just the abelian gauge potential familiar from electromagnetism, with (2 ) the usual

abelian gauge transformation. Hence, A

is known as the nonabelian gauge potential.

A transformation U that depends on the spacetime coordinates x is known as a gauge

transformation or local transformation. A Lagrangian L invariant under a gauge transfor-

mation is said to be gauge invariant.

IV.5. Nonabelian Gauge Theory | 255

Construction of the field strength

We can now immediately write a gauge invariant Lagrangian, namely

L =(D

ϕ)

†

ϕ) − V(ϕ

†

ϕ) (5)

but the gauge potential A

does not yet have dynamics of its own. In the familiar example

of U(1) gauge invariance, we have written the coupling of the electromagnetic potential

to the matter field ϕ, but we have yet to write the Maxwell term −

μν

in the

Lagrangian. Our first task is to construct a field strength F

μν

out of A

. How do we do

that? Yang and Mills apparently did it by trial and error. As an exercise you might also

want to try that before reading on.

At this point the language of differential forms introduced in chapter IV.4 proves to

be of use. It is convenient to absorb a factor of −i by defining A

≡−iA

, where A

denotes the gauge potential we have been using all along. Until further notice, when

we write A

we mean A

. Referring to (1) we see that the covariant derivative has the

cleaner form D

=∂

. (Incidentally, the superscripts M and P indicate the potential

appearing in the mathematical and physical literature, respectively.) As before, let us

introduce A = A

, now a matrix 1-form, that is, a form that also happens to be a matrix

in the defining representation of the Lie algebra [e.g., an N by N traceless hermitean matrix

for SU (N).] Note that

= A

, A

]dx

is not zero for a nonabelian gauge potential. (Obviously, there is no such object in electro-

magnetism.)

Our task is to construct a 2-form F =

μν

out of the 1-form A. We adopt a direct

approach. Out of A we can construct only two possible 2-forms: dA and A

.SoF must be

a linear combination of the two.

In the notation we are using the transformation law (2) reads

A → UAU

†

+ UdU

†

(6)

with U a 0-form (and so dU

†

= ∂

†

.) Applying d to (6) we have

dA → UdAU

†

+ dUAU

†

− UAdU

†

+ dUdU

†

(7)

Note the minus sign in the third term, from moving the 1-form d past the 1-form A.On

the other hand, squaring (6) we have

→ UA

†

+ UAdU

†

+ UdU

†

UAU

†

+ UdU

†

UdU

†

(8)

Applying d to UU

†

= 1 we have UdU

†

=−dUU

†

. Thus, we can rewrite

(

)

→ UA

†

+ UAdU

†

− dUAU

†

− dUdU

†

(9)

256 | IV. Symmetry and Symmetry Breaking

Lo and behold! If we add (7) and (9), six terms knock each other off, leaving us with

something nice and clean:

dA + A

→ U(dA+ A

†

(10)

The mathematical structure thus led Yang and Mills to define the field strength

F = dA + A

(11)

Unlike A, the field strength 2-form F transforms homogeneously (10):

F → UFU

†

(12)

In the abelian case A

vanishes and F reduces to the usual electromagnetic form. In the

nonabelian case, F is not gauge invariant, but gauge covariant.

Of course, you can also construct F

μν

without using differential forms. As an exercise

you should do it starting with (4). The exercise will make you appreciate differential forms!

At the very least, we can regard differential forms as an elegantly compact notation that

suppresses the indices a and μ in (4). At the same time, the fact that (11) emerges so

smoothly clearly indicates a profound underlying mathematical structure. Indeed, there

is a one-to-one translation between the physicist’s language of gauge theory and the

mathematician’s language of fiber bundles.

Let me show you another route to (11). In analogy to d , define D = d +A, understood

as an operator acting on a form to its right. Let us calculate

= (d + A)(d +A) = d

+ dA + Ad + A

The first term vanishes, the second can be written as dA = (dA) − Ad; the parenthesis

emphasizes that d acts only on A. Thus,

= (dA) + A

= F (13)

Pretty slick? I leave it as an exercise for you to show that D

transforms homogeneously

and hence so does F .

Elegant though differential forms are, in physics it is often desirable to write more

explicit formulas. We can write (11) out as

F = (∂

+ A

)dx

(∂

− ∂

+ [A

, A

])dx

(14)

With the definition F ≡

μν

we have

μν

= ∂

− ∂

+ [A

, A

] (15)

At this point, we might also want to switch back to physicist’s notation. Recall that A

in (15) is actually A

≡−iA

and so by analogy define F

μν

=−iF

μν

. Thus,

μν

= ∂

− ∂

− i[A

, A

] (16)

where, until further notice, A

stands for A

. (One way to see the necessity for the i in (16)

is to remember that physicists like to take A

to be a hermitean matrix and the commutator

of two hermitean matrices is antihermitean.)

IV.5. Nonabelian Gauge Theory | 257

As long as we are being explicit we might as well go all the way and exhibit the group

indices as well as the Lorentz indices. We already wrote A

= A

and so we naturally

write F

μν

= F

μν

. Then (16) becomes

μν

= ∂

− ∂

+ f

abc

(17)

I mention in passing that for SU(2)Aand F transform as vectors and the structure

constant f

abc

is just ε

abc

, so the vector notation



μν

= ∂



− ∂



is often

used.

The Yang-Mills Lagrangian

Given that F transforms homogeneously (12) we can immediately write down the analog

of the Maxwell Lagrangian, namely the Yang-Mills Lagrangian

L =−

tr F

μν

(18)

We are normalizing T

by tr T

so that L =−(1/4g

μν

aμν

. The theory

described by this Lagrangian is known as pure Yang-Mills theory or nonabelian gauge

theory.

Apart from the quadratic term (∂

− ∂

)

, the Lagrangian L =−(1/4g

μν

aμν

also contains a cubic term f

abc

bμ

cν

(∂

− ∂

) and a quartic term (f

abc

)

As in electromagnetism the quadratic term describes the propagation of a massless vector

boson carrying an internal index a, known as the nonabelian gauge boson or the Yang-

Mills boson. The cubic and quartic terms are not present in electromagnetism and describe

the self-interaction of the nonabelian gauge boson. The corresponding Feynman rules are

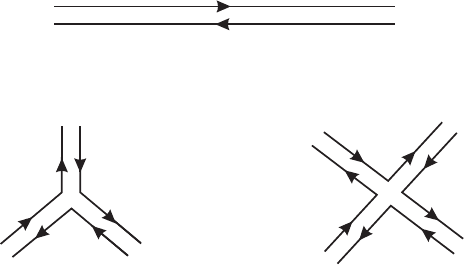
given in figure IV.5.1a, 1b, and c.

The physics behind this self-interaction of the Yang-Mills bosons is not hard to under-

stand. The photon couples to charged fields but is not charged itself. Just as the charge

(c)

(b)

(a)

Figure IV.5.1

258 | IV. Symmetry and Symmetry Breaking

of a field tells us how the field transforms under the U(1) gauge group, the analog of the

charge of a field in a nonabelian gauge theory is the representation the field belongs to. The

Yang-Mills bosons couple to all fields transforming nontrivially under the gauge group. But

the Yang-Mills bosons themselves transform nontrivially: In fact, as we have noted, they

transform under the adjoint representation. Thus, they must couple to themselves.

Pure Maxwell theory is free and so essentially trivial. It contains a noninteracting photon.

In contrast, pure Yang-Mills theory contains self-interaction and is highly nontrivial. Note

that the structure coefficients f

abc

are completely fixed by group theory, and thus in

contrast to a scalar field theory, the cubic and quartic self-interactions of the gauge bosons,

including their relative strengths, are totally fixed by symmetry. If any 4-dimensional field

theory can be solved exactly, pure Yang-Mills theory may be it, but in spite of the enormous

amount of theoretical work devoted to it, it remains unsolved (see chapters VII.3 and VII.4).

’t Hooft’s double-line formalism

While it is convenient to use the component fields A

for many purposes, the matrix

field A

= A

embodies the mathematical structure of nonabelian gauge theory more

elegantly. The propagator for the components of the matrix field in a U(N) gauge theory

has the form

0|TA

(x)

(0)

|0

=0|TA

(x)A

(0) |0(T

)

(19)

∝ δ

)

∝ δ

[We have gone from an SU (N) to a U(N) theory for the sake of simplicity. The generators

of SU(N ) satisfy a traceless condition TrT

= 0, as a result of which we would have to

subtract

from the right-hand side.] The matrix structure A

μj

naturally suggests that

we, following ’t Hooft, introduce a double-line formalism, in which the gauge potential is

described by two lines, each associated with one of the two indices i and j . We choose the

convention that the upper index flows into the diagram, while the lower index flows out

of the diagram. The propagator in (19) is represented in figure IV.5.2a. The double-line

formalism allows us to reproduce the index structure δ

naturally. The cubic and quartic

couplings are represented in figure IV.5.2b and c.

The constant g introduced in (18) is known as the Yang-Mills coupling constant. We can

always write the quadratic term in (18) in the convention commonly used in electromag-

netism by a trivial rescaling A →gA. After this rescaling, the cubic and quartic couplings

of the Yang-Mills boson go as g and g

, respectively. The covariant derivative in (1) be-

comes D

ϕ = ∂

ϕ − igA

ϕ, showing that g also measures the coupling of the Yang-Mills

boson to matter. The convention we used, however, brings out the mathematical structure

more clearly. As written in (18), g

measures the ease with which the Yang-Mills boson can

propagate. Recall that in chapter III.7 we also found this way of defining the coupling as

IV.5. Nonabelian Gauge Theory | 259

(a)

(b)

(c)

Figure IV.5.2

a measure of propagation useful in electromagnetism. We will see in chapter VIII.1 that

Newton’s coupling appears in the same way in the Einstein-Hilbert action for gravity.

The θ term

Besides tr F

μν

, we can also form the dimension-4 term ε

μνλρ

tr F

μν

λρ

. Clearly,

this term violates time reversal invariance T and parity P since it involves one time

index and three space indices. We will see later that the strong interaction is described

by a nonabelian gauge theory, with the Lagrangian containing the so-called θ term

(θ/32π

)ε

μνλρ

tr F

μν

λρ

. As you will show in exercise IV.5.3 this term is a total diver-

gence and does not contribute to the equation of motion. Nevertheless, it induces an

electric dipole moment for the neutron. The experimental upper bound on the electric

dipole moment for the neutron translates into an upper bound on θ of the order 10

−9

will not go into how particle physicists resolve the problem of making sure that θ is small

enough or vanishes outright.

Coupling to matter fields

We took the scalar field ϕ to transform in the fundamental representation of the group.

In general, ϕ can transform in an arbitrary representation R of the gauge group G.We

merely have to write the covariant derivative more generally as

ϕ = (∂

− iA

(R)

)ϕ (20)

where T

(R)

represents the ath generator in the representation R (see exercise IV.5.1).

Clearly, the prescription to turn a globally symmetric theory into a locally symmetric

theory is to replace the ordinary derivative ∂

acting on any field, boson or fermion,

260 | IV. Symmetry and Symmetry Breaking

belonging to the representation R by the covariant derivative D

=(∂

−iA

(R)

). Thus,

the coupling of the nonabelian gauge potential to a fermion field is given by

L =

ψ(iγ

− m)ψ =

ψ(iγ

∂

+ γ

(R)

− m)ψ . (21)

Fields listen to the Yang-Mills gauge bosons according to the representation R that

they belong to, and those that belong to the trivial identity representation do not hear

the call of the gauge bosons. In the special case of a U(1) gauge theory, also known as

electromagnetism, R corresponds to the electric charge of the field. Those fields that

transform trivially under U(1) are electrically neutral.

Appendix

Let me show you another context, somewhat surprising at first sight, in which the Yang-Mills structure pops up.

Consider Schr

odinger’s equation

∂

∂t

(t) = H(t)(t) (22)

with a time dependent Hamiltonian H(t). The setup is completely general: For instance, we could be talking

about spin states in a magnetic field or about a single particle nonrelativistic Hamiltonian with the wave function

(x , t). We suppress the dependence of H and  on variables other than time t.

First, solve the eigenvalue problem of H(t). Suppose that because of symmetry or some other reason the

spectrum of H(t) contains an n-fold degeneracy, in other words, there exist n distinct solutions of the equations

H(t)ψ

(t) = E(t)ψ

(t), with a = 1,

...

, n. Note that E(t) can vary with time and that we are assuming that the

degeneracy persists with time, that is, the degeneracy does not occur “accidentally” at one instant in time. We can

always replace H(t)by H(t)− E(t) so that henceforth we have H(t)ψ

(t) = 0. Also, the states can be chosen to

be orthogonal so that ψ

(t)|ψ

(t)=δ

. (For notational reasons it is convenient to jump back and forth between

the Schr

odinger and the Dirac notation. To make it absolutely clear, we have

ψ

(t)|ψ

(t)=



d xψ

∗

(x, t)ψ

(x, t)

if we are talking about single particle quantum mechanics.)

Let us now study (22) in the adiabatic limit, that is, we assume that the time scale over which H(t) varies is

much longer than 1/E, where E denotes the energy gap separating the states ψ

(t) from neighboring states.

In that case, if (t) starts out in the subspace spanned by {ψ

(t)} it will stay in that subspace and we can write

(t) =



(t)ψ

(t). Plugging this into (22) we obtain immediately



[(dc

/dt)ψ

(t) + c

(t)(∂ψ

/∂t)] = 0.

Taking the scalar product with ψ

(t), we obtain

=−



(23)

with the n by n matrix

(t) ≡ iψ

(t)|

∂ψ

∂t

 (24)

Now suppose somebody else decides to use a different basis, ψ



(t) = U

∗

(t)ψ

(t), related to ours by a unitary

transformation. (The complex conjugate on the unitary matrix U is just a notational choice so that our final

equation will come out looking the same as a celebrated equation in the text; see below.) I have also passed

F. Wilczek and A. Zee, “Appearance of Gauge Structure in Simple Dynamical Systems,” Phys. Rev. Lett.

52:2111, 1984.

IV.5. Nonabelian Gauge Theory | 261

to the repeated indices summed notation. Differentiate to obtain (∂ψ



/∂t) = U

∗

(t)(∂ψ

/∂t) + (dU

∗

/dt)ψ

(t).

Contracting this with ψ

∗

(t) = U

(t)ψ

∗

(t) and multiplying by i,wefind



= UAU

†

+ iU

∂U

†

∂t

(25)

Suppose the Hamiltonian H(t)depends on d parameters λ

...

, λ

. We vary the parameters, thus tracing out a

path definedby {λ

(t), μ =1,

...

, d}in the d-dimensional parameter space. For example, for a spin Hamiltonian,

{λ

} could represent an external magnetic field. Now (23) becomes

=−



)

dλ

(26)

if we define (A

)

≡ iψ

|∂

, where ∂

≡ ∂/∂λ

, and (25) generalizes to



= UA

†

+ iU∂

†

(27)

We have recovered (IV.5.2). Lo and behold, a Yang-Mills gauge potential A

has popped up in front of our very

eyes!

The “transport” equation (26) can be formally solved by writing c(λ) = Pe

−



dλ

, where the line integral

is over a path connecting an initial point in the parameter space to some final point λ and P denotes a path

ordering operation. We break the path into infinitesimal segments and multiply together the noncommuting

contribution e

−A

λ

from each segment, ordered along the path. In particular, if the path is a closed curve, by

the time we return to the initial values of the parameters, the wave function will have acquired a matrix phase

factor, known as the nonabelian Berry’s phase. This discussion is clearly intimately related to the discussion of

the Aharonov-Bohm phase in the preceding chapter.

To see this nonabelian phase, all we have to do is to find some quantum system with degeneracy in its spectrum

and vary some external parameter such as a magnetic field.

In their paper, Yang and Mills spoke of the degeneracy

of the proton and neutron under isospin in an idealized world and imagined transporting a proton from one point

in the universe to another. That a proton at one point can be interpreted as a neutron at another necessitates the

introduction of a nonabelian gauge potential. I find it amusing that this imagined transport can now be realized

analogously in the laboratory.

You will realize that the discussion here parallels the discussion in the text leading up to (IV.5.2). The spacetime

dependent symmetry transformation corresponds to a parameter dependent change of basis. When I discuss

gravity in chapter VIII.1 it will become clear that moving the basis {ψ

} around in the parameter space is the

precise analog of parallel transporting a local coordinate frame in differential geometry and general relativity. We

will also encounter the quantity Pe

−



dλ

again in chapter VII.1 in the guise of a Wilson loop.

Exercises

IV.5.1 Write down the Lagrangian of an SU(2) gauge theory with a scalar field in the I = 2 representation.

IV.5.2 Prove the Bianchi identity DF ≡dF +[A, F ] =0. Write this out explicitly with indices and show that in

the abelian case it reduces to half of Maxwell’s equations.

IV.5.3 In 4-dimensions ε

μνλρ

tr F

μν

λρ

can be written as tr F

. Show that d tr F

= 0 in any dimensions.

IV.5.4 Invoking the Poincar

e lemma (IV.4.5) and the result of exercise IV.5.3 show that tr F

=d tr(AdA +

Write this last equation out explicitly with indices. Identify these quantities in the case of electromag-

netism.

A. Zee, “On the Non-Abelian Gauge Structure in Nuclear Quadrupole Resonance,” Phys. Rev. A38:1, 1988.

The proposed experiment was later done by A. Pines.