Zee A. Quantum Field Theory in a Nutshell

Подождите немного. Документ загружается.

262 | IV. Symmetry and Symmetry Breaking

IV.5.5 For a challenge show that tr F

, which appears in higher dimensional theories such as string theory, are

all total divergences. In other words, there exists a (2n −1)-form ω

2n−1

(A) such that tr F

=dω

2n−1

(A).

[Hint: A compact representation of the form ω

2n−1

(A) =



dt f

2n−1

(t , A) exists.] Work out ω

(A)

explicitly and try to generalize knowing ω

and ω

. Determine the (2n −1)-form f

2n−1

(t , A). For help,

see B. Zumino et al., Nucl. Phys. B239:477, 1984.

IV.5.6 Write down the Lagrangian of an SU(3) gauge theory with a fermion field in the fundamental or defining

triplet representation.

IV.6 The Anderson-Higgs Mechanism

The gauge potential eats the Nambu-Goldstone boson

As I noted earlier the ability to ask good questions is of crucial importance in physics.

Here is an excellent question: How does spontaneous symmetry breaking manifest itself

in gauge theories?

Going back to chapter IV.1, we gauge the U(1) theory in (IV.1.6) by replacing ∂

ϕ with

ϕ = (∂

− ieA

)ϕ so that

L =−

μν

+ (Dϕ)

†

Dϕ + μ

†

ϕ − λ(ϕ

†

ϕ)

(1)

Now when we go to polar coordinates ϕ = ρe

iθ

we have D

ϕ = [∂

ρ + iρ(∂

θ −eA

)]e

iθ

and thus

L =−

μν

+ ρ

(∂

θ −eA

)

+ (∂ρ)

+ μ

− λρ

(2)

(Compare this with L =ρ

(∂

θ)

+(∂ρ)

+μ

−λρ

in the absence of the gauge field.)

Under a gauge transformation ϕ → e

iα

ϕ (so that θ → θ + α) and eA

→eA

+∂

α, and

thus the combination B

≡ A

− (1/e)∂

θ is gauge invariant. The first two terms in L

thus become −

μν

. Note that F

μν

=∂

−∂

=∂

−∂

has the

same form in terms of the potential B

Upon spontaneous symmetry breaking, we write ρ = (1/

√

2)(v + χ), with v =



/λ.

Hence

L =−

μν

+ e

vχB

(∂χ )

− μ

−

√

λμχ

−

4λ

(3)

264 | IV. Symmetry and Symmetry Breaking

The theory now consists of a vector field B

with mass

M = ev (4)

interacting with a scalar field χ with mass

√

2μ. The phase field θ , which would have been

the Nambu-Goldstone boson in the ungauged theory, has disappeared. We say that the

gauge field A

has eaten the Nambu-Goldstone boson; it has gained weight and changed

its name to B

Recall that a massless gauge field has only 2 degrees of freedom, while a massive gauge

field has 3 degrees of freedom. A massless gauge field has to eat a Nambu-Goldstone boson

in order to have the requisite number of degrees of freedom. The Nambu-Goldstone

boson becomes the longitudinal degree of freedom of the massive gauge field. We do not

lose any degrees of freedom, as we had better not.

This phenomenon of a massless gauge field becoming massive by eating a Nambu-

Goldstone boson was discovered by numerous particle physicists

and is known as the

Higgs mechanism. People variously call ϕ , or more restrictively χ , the Higgs field. The

same phenomenon was discovered in the context of condensed matter physics by Landau,

Ginzburg, and Anderson, and is known as the Anderson mechanism.

Let us give a slightly more involved example, an O(3) gauge theory with a Higgs field ϕ

(a =1, 2, 3 ) transforming in the vector representation. The Lagrangian contains the kinetic

energy term

)

, with D

= ∂

+ gε

abc

as indicated in (IV.5.20). Upon

spontaneous symmetry breaking, ϕ acquires a vacuum expectation value which without

loss of generality we can choose to point in the 3-direction, so that ϕ

=vδ

. We set

= v and see that

)

→

(gv)

μ1

+ A

μ2

) (5)

The gauge potential A

and A

acquires mass gv [compare with (4)] while A

remains

massless.

A more elaborate example is that of an SU(5) gauge theory with ϕ transforming as the 24-

dimensional adjoint representation. (See appendix B for the necessary group theory.) The

field ϕ isa5by5hermitean traceless matrix. Since the adjoint representation transforms

as ϕ → ϕ + iθ

, ϕ], we have D

ϕ = ∂

ϕ − igA

, ϕ] with a = 1,

...

, 24 running

over the 24 generators of SU(5). By a symmetry transformation the vacuum expectation

value of ϕ can be taken to be diagonal ϕ

=v

(i, j = 1,

...

,5), with



=0 . (This

is the analog of our choosing ϕ to point in the 3-direction in the preceding example.) We

have in the Lagrangian

tr(D

ϕ)(D

ϕ) → g

tr[T

, ϕ][ϕ, T

μb

(6)

The gauge boson masses squared are given by the eigenvalues of the 24 by 24 matrix

tr[T

, ϕ][ϕ, T

], which we can compute laboriously for any given ϕ.

Including P. Higgs, F. Englert, R. Brout, G. Guralnik, C. Hagen, and T. Kibble.

IV.6. Anderson-Higgs Mechanism | 265

It is easy to see, however, which gauge bosons remain massless. As a specific example

(which will be of interest to us in chapter VII.6), suppose

ϕ=v

⎛

⎜

⎝

200 0 0

020 0 0

002 0 0

000−30

000 0 −3

⎞

⎟

⎠

(7)

Which generators T

commute with ϕ? Clearly, generators of the form



A 0



and of the

form



0 B



. Here A represents 3 by 3 hermitean traceless matrices (of which there are

−1 = 8, the so-called Gell-Mann matrices) and B represents 2 by 2 hermitean traceless

matrices (of which there are 2

− 1 = 3, namely the Pauli matrices). Furthermore, the

generator

⎛

⎜

⎝

200 0 0

020 0 0

002 0 0

000−30

000 0 −3

⎞

⎟

⎠

(8)

being proportional to ϕ, obviously commutes with ϕ. Clearly, these generators gen-

erate SU(3), SU(2), and U(1), respectively. Thus, in the 24 by 24 mass-squared matrix

tr[T

, ϕ][ϕ, T

] there are blocks of submatrices that vanish, namely, an 8 by 8 block,

a 3 by 3 block, anda1by1block. We have 8 + 3 + 1 = 12 massless gauge bosons. The

remaining 24 − 12 = 12 gauge bosons acquire mass.

Counting massless gauge bosons

In general, consider a theory with the global symmetry group G spontaneously broken to

a subgroup H . As we learned in chapter IV.1, n(G) − n(H ) Nambu-Goldstone bosons

appear. Now suppose the symmetry group G is gauged. We start with n(G) massless

gauge bosons, one for each generator. Upon spontaneous symmetry breaking, the n(G) −

n(H ) Nambu-Goldstone bosons are eaten by n(G) − n(H ) gauge bosons, leaving n(H )

massless gauge bosons, exactly the right number since the gauge bosons associated with

the surviving gauge group H should remain massless.

In our simple example, G = U(1), H = nothing: n(G) =1 and n(H ) =0. In our second

example, G = O(3), H = O(2)  U(1) : n(G) = 3 and n(H ) = 1, and so we end up with

one massless gauge boson. In the third example, G =SU(5), H = SU(3) ⊗ SU(2) ⊗U(1)

so that n(G) = 24 and n(H ) = 12. Further examples and generalizations are worked out

in the exercises.

266 | IV. Symmetry and Symmetry Breaking

Gauge boson mass spectrum

It is easy enough to work out the mass spectrum explicitly. The covariant derivative of a

Higgs field is D

ϕ =∂

ϕ +gA

ϕ, where g is the gauge coupling, T

are the generators

of the group G when acting on ϕ, and A

the gauge potential corresponding to the ath

generator. Upon spontaneous symmetry breaking we replace ϕ by its vacuum expectation

value ϕ=v. Hence D

ϕ is replaced by gA

v. The kinetic term

ϕ) [here

(

) denotes the scalar product in the group G] in the Lagrangian thus becomes

v)A

μa

≡

μa

(μ

)

where we have introduced the mass-squared matrix

(μ

)

= g

v) (9)

for the gauge bosons. [You will recognize (9) as the generalization of (4); also compare (5)

and (6).] We diagonalize (μ

)

to obtain the masses of the gauge bosons. The eigenvectors

tell us which linear combinations of A

correspond to mass eigenstates.

Note that μ

is an n(G) by n(G) matrix with n(H ) zero eigenvalues, whose existence can

also be seen explicitly. Let T

be a generator of H . The statement that H remains unbroken

by the vacuum expectation value v means that the symmetry transformation generated by

leaves v invariant; in other words, T

v =0, and hence the gauge boson associated with

remains massless, as it should. All these points are particularly evident in the SU(5)

example we worked out.

Feynman rules in spontaneously broken gauge theories

It is easy enough to derive the Feynman rules for spontaneously broken gauge theories.

Take, for example, (3). As usual, we look at the terms quadratic in the fields, Fourier

transform, and invert. We see that the gauge boson propagator is given by

−i

− M

+ iε

μν

−

) (10)

and the χ propagator by

− 2μ

+ iε

(11)

I leave it to you to work out the rules for the interaction vertices.

As I said in another context, field theories often exist in several equivalent forms.

Take the U(1) theory in (1) and instead of polar coordinates go to Cartesian coordinates

ϕ = (1/

√

2)(ϕ

+ iϕ

) so that

ϕ = ∂

ϕ − ieA

ϕ =

√

[(∂

+ eA

) + i(∂

− eA

)]

IV.6. Anderson-Higgs Mechanism | 267

Then (1) becomes

L =−

μν

[(∂

+ eA

)

+ (∂

− eA

)

] (12)

(ϕ

+ ϕ

) −

λ(ϕ

+ ϕ

)

Spontaneous symmetry breaking means setting ϕ

→ v + ϕ



with v =



/λ.

The physical content of (12) and (3) should be the same. Indeed, expand the Lagrangian

(12) to quadratic order in the fields:

L =

4λ

−

μν

− MA

∂

[(∂



)

− 2μ

2

]

(∂

)

...

(13)

The spectrum, a gauge boson A with mass M =ev and a scalar boson ϕ



with mass

√

2μ,

is identical to the spectrum in (3). (The particles there were named B and χ .)

But oops, you may have noticed something strange: the term −MA

∂

which mixes

the fields A

and ϕ

. Besides, why is ϕ

still hanging around? Isn’t he supposed to have

been eaten? What to do?

We can of course diagonalize but it is more convenient to get rid of this mixing term.

Referring to the Fadeev-Popov quantization of gauge theories discussed in chapter III.4 we

note that the gauge fixing term generates a term to be added to L. We can cancel the unde-

sirable mixing term by choosing the gauge function to be f (A) = ∂A + ξevϕ

−σ . Going

through the steps, we obtain the effective Lagrangian L

eff

= L − (1/2ξ)(∂A + ξMϕ

)

[compare with (III.4.7)]. The undesirable cross term −MA

∂

in L is now canceled upon

integration by parts. In L

eff

the terms quadratic in A now read −

μν

−

(1/2ξ)(∂A)

while the terms quadratic in ϕ

read

[(∂

)

−ξM

], immediately giving

us the gauge boson propagator

−i

− M

+ iε



μν

− (1 − ξ)

− ξM

+ iε



(14)

and the ϕ

propagator

− ξM

+ iε

(15)

This one-parameter class of gauge choices is known as the R

gauge. Note that the would-

be Goldstone field ϕ

remains in the Lagrangian, but the very fact that its mass depends on

the gauge parameter ξ brands it as unphysical. In any physical process, the ξ dependence in

the ϕ

and A propagators must cancel out so as to leave physical amplitudes ξ independent.

In exercise IV.6.9 you will verify that this is indeed the case in a simple example.

Different gauges have different advantages

You might wonder why we would bother with the R

gauge. Why not just use the equivalent

formulation of the theory in (3), known as the unitary gauge, in which the gauge boson

268 | IV. Symmetry and Symmetry Breaking

propagator (10) looks much simpler than (14) and in which we don’t have to deal with the

unphysical ϕ

field? The reason is that the R

gauge and the unitary gauge complement

each other. In the R

gauge, the gauge boson propagator (14) goes as 1/k

for large k and

so renormalizability can be proved rather easily. On the other hand, in the unitary gauge

all fields are physical (hence the name “unitary”) but the gauge boson propagator (10)

apparently goes as k

for large k; to prove renormalizability we must show that the

piece of the propagator does not contribute. Using both gauges, we can easily prove

that the theory is both renormalizable and unitary. By the way, note that in the limit ξ →∞

(14) goes over to (10) and ϕ

disappear, at least formally.

In practical calculations, there are typically many diagrams to evaluate. In the R

gauge,

the parameter ξ darn well better disappears when we add everything up to form the physical

mass shell amplitude. The R

gauge is attractive precisely because this requirement

provides a powerful check on practical calculations.

I remarked earlier that strictly speaking, gauge invariance is not so much a symmetry

as the reflection of a redundancy in the degrees of freedom used. (The photon has only 2

degrees of freedom but we use a field A

with 4 components.) A purist would insist, in

the same vein, that there is no such thing as spontaneously breaking a gauge symmetry.

To understand this remark, note that spontaneous breaking amounts to setting ρ ≡|ϕ| to

v and θ to 0 in (2). The statement |ϕ|=v is perfectly U(1) invariant: It defines a circle in ϕ

space. By picking out the point θ =0 on the circle in a globally symmetric theory we break

the symmetry. In contrast, in a gauge theory, we can use the gauge freedom to fix θ = 0

everywhere in spacetime. Hence the purists. I will refrain from such hair-splitting in this

book and continue to use the convenient language of symmetry breaking even in a gauge

theory.

Exercises

IV.6.1 Consider an SU(5) gauge theory with a Higgs field ϕ transforming as the 5-dimensional representation:

, i =1, 2,

...

, 5. Show that a vacuum expectation value of ϕ breaks SU(5) to SU(4). Now add another

Higgs field ϕ



, also transforming as the 5-dimensional representation. Show that the symmetry can either

remain at SU(4) or be broken to SU(3).

IV.6.2 In general, there may be several Higgs fields belonging to various representations labeled by α. Show that

the mass squared matrix for the gauge bosons generalize immediately to (μ

)



where v

is the vacuum expectation value of ϕ

and T

is the ath generator represented on ϕ

. Combine

the situations described in exercises IV.6.1 and IV.6.2 and work out the mass spectrum of the gauge

bosons.

IV.6.3 The gauge group G does not have to be simple; it could be of the form G

⊗ G

⊗

...

⊗ G

, with

coupling constants g

, g

...

, g

. Consider, for example, the case G = SU(2) ⊗ U(1) and a Higgs

field ϕ transforming like the doublet under SU(2) and like a field with charge

under U(1), so that

ϕ = ∂

ϕ − i[gA

(τ

/2) + g



] ϕ. Let ϕ=





. Determine which linear combinations of the

gauge bosons A

and B

acquire mass.

IV.6.4 In chapter IV.5 you worked out an SU(2) gauge theory with a scalar field ϕ in the I = 2 representation.

Write down the most general quartic potential V(ϕ)and study the possible symmetry breaking pattern.

IV.6. Anderson-Higgs Mechanism | 269

IV.6.5 Complete the derivation of the Feynman rules for the theory in (3) and compute the amplitude for the

physical process χ +χ →B + B .

IV.6.6 Derive (14). [Hint: The procedure is exactly the same as that used to obtain (III.4.9).] Write L =

μν

with Q

μν

= (∂

+ M

μν

− [1 − (1/ξ)]∂

∂

or in momentum space Q

μν

=−(k

− M

μν

+ [1 −

(1/ξ)]k

. The propagator is the inverse of Q

μν

IV.6.7 Work out the (

...

) in (13) and the Feynman rules for the various interaction vertices.

IV.6.8 Using the Feynman rules derived in exercise IV.6.7 calculate the amplitude for the physical process ϕ



→A + A and show that the dependence on ξ cancels out. Compare with the result in exercise IV.6.5.

[Hint: There are two diagrams, one with A exchange and the other with ϕ

exchange.]

IV.6.9 Consider the theory defined in (12) with μ = 0. Using the result of exercise IV.3.5 show that

eff

(ϕ) =

λϕ

64π

(10λ

+ 3e

)ϕ



log

−



...

(16)

where ϕ

= ϕ

+ ϕ

. This potential has a minimum away from ϕ =0 and thus the gauge symmetry

is spontaneously broken by quantum fluctuations. In chapter IV.3 we did not have the e

term and

argued that the minimum we got there was not to be trusted. But here we can balance the λϕ

against

log(ϕ

) for λ of the same order of magnitude as e

. The minimum can be trusted. Show that

the spectrum of this theory consists of a massive scalar boson and a massive vector boson, with

(scalar)

(vector)

2π

4π

(17)

For help, see S. Coleman and E. Weinberg, Phys. Rev. D7: 1888, 1973.

IV.7 Chiral Anomaly

Classical versus quantum symmetry

I have emphasized the importance of asking good questions. Here is another good one: Is

a symmetry of classical physics necessarily a symmetry of quantum physics?

We have a symmetry of classical physics if a transformation ϕ → ϕ + δϕ leaves the action

S(ϕ) invariant. We have a symmetry of quantum physics if the transformation leaves the

path integral



Dϕe

iS(ϕ)

invariant.

When our question is phrased in this path integral language, the answer seems obvious:

Not necessarily. Indeed, the measure Dϕ may or may not be invariant.

Yet historically, field theorists took as almost self-evident the notion that any symmetry

of classical physics is necessarily a symmetry of quantum physics, and indeed, almost

all the symmetries they encountered in the early days of field theory had the property of

being symmetries of both classical and quantum physics. For instance, we certainly expect

quantum mechanics to be rotational invariant. It would be very odd indeed if quantum

fluctuations were to favor a particular direction.

You have to appreciate the frame of mind that field theorists operated in to understand

their shock when they discovered in the late 1960s that quantum fluctuations can indeed

break classical symmetries. Indeed, they were so shocked as to give this phenomenon the

rather misleading name “anomaly,” as if it were some kind of sickness of field theory. With

the benefits of hindsight, we now understand the anomaly as being no less conceptually

innocuous as the elementary fact that when we change integration variables in an integral

we better not forget the Jacobian.

With the passing of time, field theorists have developed many different ways of looking

at the all important subject of anomaly. They are all instructive and shed different lights

on how the anomaly comes about. For this introductory text I choose to show the existence

of anomaly by an explicit Feynman diagram calculation. The diagram method is certainly

more laborious and less slick than other methods, but the advantage is that you will see

IV.7. Chiral Anomaly | 271

a classical symmetry vanishing in front of your very eyes! No smooth formal argument

for us.

The lesser of two evils

Consider the theory of a single massless fermion L =

ψiγ

∂

ψ . You can hardly ask

for a simpler theory! Recall from chapter II.1 that L is manifestly invariant under the

separate transformations ψ → e

iθ

ψ and ψ → e

iθγ

ψ , corresponding to the conserved

vector current J

ψγ

ψ and the conserved axial current J

ψγ

ψ respectively.

You should verify that ∂

= 0 and ∂

= 0 follow immediately from the classical

equation of motion iγ

∂

ψ =0.

Let us now calculate the amplitude for a spacetime history in which a fermion-anti-

fermion pair is created at x

and another such pair is created at x

by the vector current,

with the fermion from one pair annihilating the antifermion from the other pair and the

remaining fermion-antifermion pair being subsequently annihilated by the axial current.

This is a long-winded way of describing the amplitude 0|TJ

(0)J

) |0 in

words, but I want to make sure that you know what I am talking about. Feynman tells

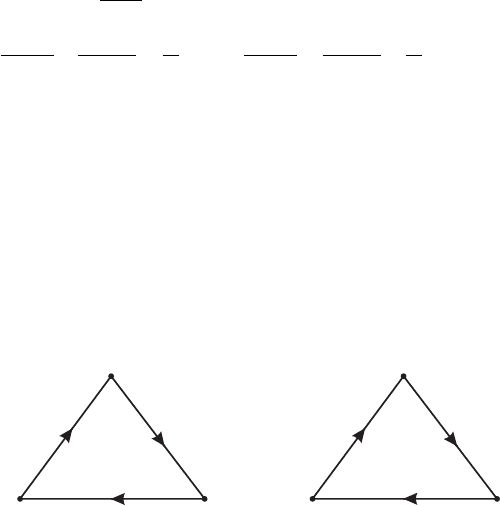
us that the Fourier transform of this amplitude is given by the two “triangle” diagrams in

figure IV.7.1a and b.



λμν

, k

) = (−1)i



(2π)



p − q

p − k

p

+ γ

p − q

p − k

p



(1)

with q = k

. Note that the two terms are required by Bose statistics. The overall factor

of (−1) comes from the closed fermion loop.

Classically, we have two symmetries implying ∂

=0 and ∂

=0. In the quantum

theory, if ∂

=0 continues to hold, then we should have k

1μ



λμν

=0 and k

2ν



λμν

=0,

and if ∂

= 0 continues to hold, then q



λμν

= 0. Now that we have things all set up,

we merely have to calculate 

λμν

to see if the two symmetries hold up under quantum

fluctuations. No big deal.

pp − q

p − k

(a)

pp − q

(b)

p − k

Figure IV.7.1